Детекция аномалий для комплексирования данных лидарной и спутниковой локализации транспортного средства

При работе важна точная локализация в робототехнике и беспилотном транспорте в задачах планирования движения, объезда препятствий [1], [2].

При локализации возникают сложности в условиях среды, когда один источник периодически выдает недостоверные данные в некоторых условиях. Например, при локализации с помощвю лидара и GPS при заезде в гараж или проезд под туннелем. В данном случае возможно пропадание актуальных данных с GPS, что представляет собой аномалию, которую необходимо обнаруживать как можно раньше. Это позволит не использовать неактуальные данные для локализации. В нашей работе мы хотим для локализации выполнить следующие подзадачи:

• •    определить положение с помощью данных с лидара и GPS по отдельности;

• •    определить корректность локализации от обоих источников и детектировать аномалии;

• •    осуществить комплексирование данных локализации с учетом аномалий. Часто эту операцию выполняют с помощью фильтра Калмана различных разновидностей [3], [4], [5], [6], [7], [8].

2.    Анализ предметной области 2.1.    Методы комплексирования данных бортовых систем локализации транспортных средств 2.2.    Общие алгоритмы детекции аномалий

В статье представлен разработанный метод комплексирования данных лидарной и спутниковой навигации AnKF, отличающийся алгоритмом детекции аномалий, и размеченный набор данных на основе симулятора беспилотного транспорта CARLA, на котором произведен детальный анализ качества как алгоритмов детекции аномалий.

При возникновении задачи комплексирования данных чаще всего используют фильтры Калмана (KF - Kalman filter) [3]. Он имеет несколько вариантов, включая extended Kalman filter (EKF) [4], unscented Kalman filter (UKF) [5] и cubature Kalman filter (CKF) [9]. Эти фильтры используются во многих приложениях, включая системы управления, робототехнику, компьютерное зрение и навигацию. Благодаря этим методам мы можем оценить матожидание следующего состояния локализации.

Очень часто когда необходимо комплексировать данные с GPS и IMU, используют ST-EKF [6], ESKF [7] и invariant Kalman filter(IKF) [8], так как данный метод работает с Lie-алгеброй и предсказывает 6DOF.

Кроме аналитических подходов к комплексированию данных существуют нейросетевые, так, например, исследователи, разработавшие MM-Loc [10], проанализировали использование RNN [11], LSTM [12] для объединения данных локализации с помощью wifi, IMU. CNN-empowered Kalman filter (CNN-KF) [13] использует фильтр Калмана для объединения нескольких источников информации, при этом использует сверточную нейронную сеть (CNN) для детекции аномалий. SL-SRCKF [14] предложенный подход позволяет предсказывать локализацию в случае отключения GPS и предсказывает внутренние коэффициенты SRCKF с помощью LSTM. UKF(PNC+MNC CNN) [15] предложен подход оптимизировать внутренние параметры UKF [16], таких как Process Noise Covariance и Measurement Noise Covariance, с помощью нейронных сетей.

В данном разделе сравним алгоритмы детекции аномалий по типу аномалии, по типу задачи. Результат сравнения представлен в табл. 1.

Алгоритмы детекции аномалий делятся на следующие типы:

Таблица 1

Классификация алгоритмов детекции аномалии

Название алгоритма	Тип алгоритма	Тип аномалии	Тип задачи
Angle-based Outlier Detector (ABOD) [17]	классический	точечные	кластеризация
К-Nearest Neighbors (KNN) [18]	классический	точечные	алгоритм ближайшего соседа
Local Outlier Factor (LOF) [19]	классический	точечные	кластеризация
Histogram-based     Outlier Detection (HBOS) [20]	классический	точечные	классификация
Isolation Forest [21]	классический	точечные	классификация
Minimum        Covariance Determinant (MCD) [22]	классический	точечные	статистический анализ
One-class SVM (OCSVM) [23]	классический	точечные	классификация
PCA (Principal Component Analysis) [24]	классический	точечные	классификация
Variational     Autoencoder (VAE) [25]	нейросетевой	точечные, коллективные	статистический анализ
Временная сверточная сеть (TCN) [26]	нейросетевой	точечные, коллективные	статистический анализ

• •    классические алгоритмы машинного обучения [17], [18], [19], [27], [20], [21], [22], [23], [24],

• •    нейросетевые алгоритмы (в данных алгоритмах используются нейронные сети) [25], [26].

Классификация по типу аномалии:

• •    Точечные аномалии - это аномалии, которые наблюдаются, если отдельный экземпляр данных сильно отличается по отношению к остальным данным [17], [18], [19], [27], [20], [21], [22], [23], [24], [25].

• •    Коллективные аномалии - это аномалии, которые наблюдаются, если последовательность связанных экземпляров данных (например, участок временного ряда) является аномальной по отношению к целому набору данных. Отдельный экземпляр данных в такой последовательности может не являться отклонением, однако совместное появление таких экземпляров является коллективной аномалией [25], [26].

Классификация по типу задачи для решения задачи аномалии:

• •    Классификация. Реализация данного метода основана на предположении о том, что при нормальных данных система может предсказывать один или несколько классов. Таким образом, экземпляр, не принадлежащий ни к одному из классов, является аномалией. Поиск аномалий проходит в два этапа: обучение и распознавание [20], [21], [23], [24].

• •    Кластеризация. Данная методика предполагает группировку похожих экземпляров в кластеры и не требует знаний о свойствах возможных отклонений. Выявление аномалий может строиться на следующем предположении: нормальные данные ближе к центру кластера, а аномальные - значительно дальше.

В случае, когда аномальные экземпляры не являются единичными, они также могут образовывать кластеры. Таким образом, их выявление строится на следующем предположении:

Нормальные данные образуют большие плотные кластеры, а аномальные - маленькие и разрозненные [17], [19].

• •    Алгоритм ближайшего соседа. Для использования данной методики необходимо определить понятие расстояния между объектами [18].

• •    Статистический анализ. При использовании этого подхода исследуется модель нормального поведения, которая затем сравнивается с реальным поведением. Если разница в реальном и предполагаем поведении системы, определяемая заданной функцией аномальности, выше установленного порога, делается вывод о наличии отклонений. Применяется предположение том, что нормальное поведение системы будет находиться в зоне высокой вероятности, в то время как выбросы - в зоне низкой [27], [22], [25], [26].

3.    Разработка метода3.1.    Постановка задачи

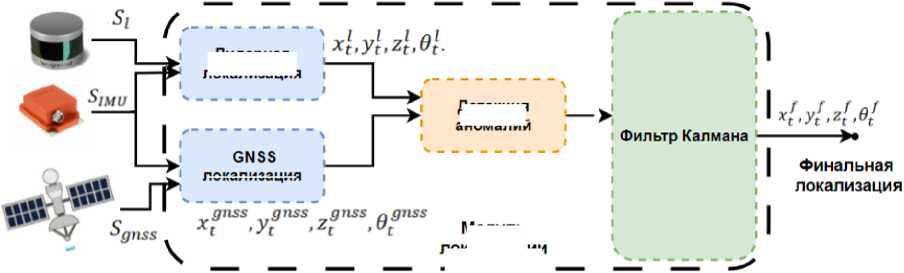
В этой задаче используются данные с лидара, которые представляют собой облако точек Si, а также да иные с GPS S_gnss и I MU S i _mu - данные в виде линейных и угловых скоростей и абсолютных значений положения и ориентации. Для локализации с помощью лидара требуется также заранее построенная лидарная карта и начальная точка расположения на данной карте. На основании этих данных строится лидарная локализация с помощью алгоритма NDT х., y^l_t, z^l_t, 9^l_t и локализация с помощью GPS x^gnss, у^дп88, z^gnss, Q^gnss_; как показано на рис. 1, выделено голубым фоном. Такие алгоритмы предсказывают абсолютные значения положения и углов поворота и их скорости.

Затем значения абсолютной локализации подаются буфер. После того как в буфере набирается необходимое число сообщений, начинает работать алгоритм детекции аномалий. Это выделено на схеме оранжевым цветом. В данной работе рассмотрено несколько алгоритмов детекции аномалий, включающие как классические, так и нейросетевые.

Отфильтрованные значения (предсказанные как аномалия) не поступают в алгоритм фильтра Калмана.

локализация

Модуль локализации

Рис. 1. Схема предложенного подхода AnKF

Лидарная локализация

Детекция аномалий

3.2.    Предложенный подход

Лидарная локализация В данном алгоритме представлена лидарная локализация на основе NDT [28], [29].

Лидарная карта M представляет с обой вектор из М то чек Xi = (x i , y i , z^ , г Е [1... М ], а х^ представляет собой k-й воксель ND с М^ точками, k-e среднее значение вокселя ND р ^ и ковариациоиная матрица S& определяются по формулам:

1   м _к

» = м У ■ г=1

1 м _к

^ к =

Д~Г 52 ^{( а} кг - Р к )(Ж кі - Р к^)Т .

^к г =1

Далее выполняется преобразование 3.О-координат исходного облака X с N точками Хі,г Е [1 ... N ] в систему координат карты M по формуле aj = R^ + t', г де R - матрица поворота, a t‘ - вектор трансляции.

Оценка соответствия (fitness) между преобразованным входным облаком точек X и эталонной лидарной картой M, представленной в виде вокселей ND, выполняется по следующей формуле:

Е ( X , R ,t‘) = £exp "^ -    )    ' - Р.>.

г

Высокие значения Е (X, R, t‘) означают, что входящее облако точек и лидарная карта хорошо ввіра.вненві. И задача оптимизации сводится к следующему виду:

arg max E( X , R , t‘).

Поэтому минимизируется функция f( R ,t‘) = -E( X , R ,t‘)

Rnew = R - H-1g, t’new = t‘ — H-1g, где g ii H частные производные и вторвю пропзводіівіе (руіікщш f.

Для выполнения данного алгоритма была заранее построена лидарная карта, которая показана на рис. 2.

Рис. 2. Карта, построенная на. основании данных с лидара.

Алгоритмы детекции аномалий В данной работе предложено использовать пороговую детекцию аномалий с преобразованием абсолютных значений положения в скорости, а также исследовать возможности различных современных обучаемых методов. Предполагается, что транспортное средство двигается по ровной поверхности. И именно поэтому учитывается только угол поворота вокруг оси z. Подробности его функционирования представлены в алгоритме 1. В результате алгоритм предсказывает, относятся ли пришедшие навигационные данные к аномалии (выход «1») или нет (выход «0»).

Алгоритм 1 Пороговая детекция аномалий qnss / qnss 1 qnss / qnss

Input x t ,x t vx^L _t+i,x^y_t+i _t,^ ,У і +г,У і +г - абсолютные значения позиционирования, 0^qnss, ^ t - абсолютные значения ориентации, At - разница между t + 1 и t.

Output 0 или 1 - не аномалия или аномалия.

Require: е >  0 ,

^vxt ^

Д+1

-

^x t

Vyt

←

sin(6 t )Mt , y t +i ^- y t cos(^ t )M t ,

qnss

^V xt

←

qnss ^x t +1

-

qnss ^x t

sin( e ^qnss)M ,

qnss

←

qnss « t +1

-

У ?

if |VXt

-

cos(9 ^qnss )At , qnss                    qnss\

^V xt I < ^{E И} \^V yt ^- V yt I

< е then return 0

else if |v X _t — v qn^ss | — ей |vL — у УП^ І — е then return 1 end if

4.    Разработка набора данных4.1.    Сбор данных с симулятора CARLA

CARLA [30] - это симулятор, который разработан для поддержки разработки, обучения и проверки систем автономного вождения. Этот симулятор предоставляет планы городов, здания, транспортные средства. Также поддерживает настройку наборов датчиков, условий окружающей среды, полный контроль над всеми динамическими объектами.

В исследуемой среде в симуляторе автомобиль оснащен RGB камерой, лидаром 32-лучевым, IMU и GPS.

Для наших дальнейших экспериментов по локализации в симуляторе CARLA выбрана карта Town03, так как на ней находится туннель, который отмечен на рис. 3 голубым прямоугольником.

В этой области образуются «аномалии» в данных глобальной спутниковой навигации GPS. Как и в реальных условиях, во время заезда в гараж или туннель данные GPS перестают менять свое значение до момента выезда из него. Именно эти данные считаются «аномалиями».

На рис. 4 справа представлено RGB изображение с камеры на автомобиле, а слева визуализировано 3D облако точек, полученное с лидара. Цветом показана дистанция до объектов. Чем ближе объекты к лидару, тем цвет ближе к фиолетовому. А чем дальше объекты, тем цвет ближе к красному.

Таблица 2

Статистика разработанных наборов данных

Параметры набора данных	Track-1	Track-2	Track-3
Размер (количество фреймов данных)	930	1210	1273
Вероятность аномалии	0.31	0.21	0.24

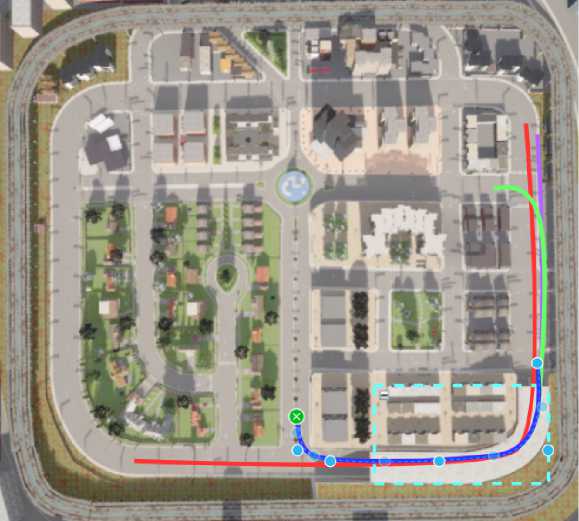
Рис. 3. Карта. Town03: Красным выделена, траектория, по которой строилась лидарная карта, зеленая траектория движения автомобиля в Track-1, сииияя - Track-2, фиолетовый - Track-3. Голубым прямоугольником выделена, область пропадания сигнала. GPS (в туннеле)

Рис. 4. Визуализация с помощью операционной системы роботов ROS: слева. - лидарпое облако точек с 32 лучевого лидара, справа. - данные с RGB камеры

Данные группировались скользящим окном отдельно по временным рядам для лидар-ной локализациии и отдельно по данным GPS локализации. Временной ряд считался аномальным, если в нем встретилась хотя бы одна, аномалия. Таким образом, был сформирован набор данных для детекции аномалий. Статистика, по его содержимому представлена, в табл. 2.

Под вероятностью аномалии понимается отношение количества подпоследовательностей данных с аномалиями на количество всех подпоследовательностей. Чем дольше автомобиль передвигался под мостом, тем больше вероятность аномалии.

5.    Результаты5.1.    Оценка качества детекции аномалий

Метриками качества, для детекции аномалий в настоящей работе являются оценки полноты (Recall) и точности (Precision), которые имеют дипазон значений от 0 до 1.

Таблица 3

Результаты оценки полноты (Recall) детекции аномалий

Алгоритм детекции аномалий	Track-1	Track-2	Track-3	Average Recall
Пороговый метод	0.4283	0.4415	0.4336	0.4345
FB [27]	0.4509	0.451	0.4511	0.4510
HBOS [20]	0.4508	0.4607	0.4611	0.4575
IForest [21]	0.3707	0.3695	0.3690	0.3697
KNN [18]	0.3280	0.3379	0.3374	0.3344
LOF [19]	0.4603	0.4596	0.4601	0.4600
РСА [24]	0.4809	0.4710	0.4706	0.4742
VAE [25]	0.6184	0.6284	0.6265	0.6244
RNN [11]	0.6292	0.6312	0.6327	0.6310
TCN [26]	0.6938	0.6857	0.6851	0.6882

В табл. 3 и 4 представлены результаты детекции аномалий алгоритмами K-Nearest neighbors (KNN) [18], local outlier factor (LOF) [19], histogram-based outlier detection (HBOS) [20], isolation forest (IForest) [21], principal component analysis(PCA) [24], variational autoencoder (VAE), временной сверточной сети (TON).

Как видно, нейросетевые методы (recurrent neural network (RNN), variational autoencoder (VAE), временная сверточная сеть (TON)) показывают значительно лучшие результаты на всех треках набора данных, чем классические обучаемые подходы (К-Nearest neighbors (KNN) [18], local outlier factor (LOF) [19], histogram-based outlier detection (HBOS) [20], isolation forest (IForest) [21], principal component analysis(PCA) [24]). Однако по точности VAE не намного уступает PGA. Таким образом, некоторые классические алгоритмы показывают сравнимые по точности результаты при достаточно хорошей настойке параметров.

Наиболее качественным методом является подход TCN, основанный на глубокой сверточной нейронной сети, которая позволяет автоматически сформировать признаки для дальнейшей классификации аномалий. Он более чем на 31.1% и 30% по метрикам полноты и точности превосходит наилучший классический обучаемый метод РСА. Также он на 8.5% и 18.9% по полноте и точности лучше, чем другой наиболее качественный нейросетевой алгоритм.

Предложенный аналитический пороговый подход превосходит ряд классических обучаемых методов (IForest, KNN), но существенно уступает нейросетевым обучаемым методам детекции аномалий.

Таблица 4

Результаты оценки точности (Precision) детекции аномалий

Алгоритм детекции аномалий	Track-1	Track-2	Track-3	Average Precision
Пороговый метод	0.2673	0.3027	0.2967	0.2889
FB [27]	0.3421	0.3911	0.3913	0.3748
HBOS [20]	0.3421	0.3760	0.3783	0.3655
IForest [21]	0.2368	0.2368	0.2358	0.2365
KNN [18]	0.2105	0.2515	0.2504	0.2375
LOF [19]	0.3421	0.3537	0.3544	0.3501
РСА [24]	0.3947	0.4027	0.4033	0.4002
VAE [25]	0.3684	0.3774	0.3798	0.3752
RNN [11]	0.4601	0.4653	0.4651	0.4635
TCN [26]	0.5635	0.5758	0.5764	0.5719

Таблица 5

Результаты оценки ошибки локализации после детекции аномалий, метрика качества АРЕ, м

Алгоритм детекции аномалий	Track-01	Track-02	Track-03	Average APE
ЕКЕ [4]	0.8155	0.8710	0.7805	0.8223
АпКЕ (Пороговый метод)	0.4015	0.3815	0.4065	0.3965
АпКЕ (ЕВ)	0.8010	0.7801	0.7135	0.7648
АпКЕ (HBOS)	0.8145	0.8645	0.8321	0.8370
АпКЕ (IF)	0.8885	0.8160	0.7934	0.8326
АпКЕ (KNN)	0.4125	0.3810	0.4037	0.3991
АпКЕ (LOF)	0.3755	0.3465	0.3921	0.3713
АпКЕ (РСА)	0.4825	0.4846	0.4709	0.4793
АпКЕ (VAE)	0.3190	0.2945	0.3267	0.3134
АпКЕ (RNN)	0.3107	0.3109	0.3241	0.3152
АпКЕ (TCN)	0.3065	0.3115	0.3096	0.3092

5.2.    Оценка качества комплексирования лидарной и спутниковой локализации

Для оценки метрики качества локализации использована стандартная метрика качества для оценки ошибки локализации АРЕ [31]. На основании данных из табл. 5 можно сделать вывод, что алгоритм комплексирования АпКЕ даже с простой пороговой детекцией аномалий улучшает локализацию. При этом применение пороговой детекции позволяет превзойти большинство классических обучаемых алгоритмов обнаружения аномалий. Это связано с тем, что довольно продолжительное время (во время проезда под туннелем) данные GPS дают неверную локализацию, для обработки именно таких ситуаций разрабатывался предложенный пороговый метод.

Алгоритмы, которые показывали наилучшие результаты по полноте и точности детекции аномалий (VAE, RNN, TCN), также демонстрируют лучшие результаты по локализации при применении в составе комплексного подхода АпКЕ.

Наиболее качественного результата на всех треках разработанного набора данных достигает подход АпКЕ, использующий метод детекции аномалий TCN. Ошибка локализации составляет в среднем менее 31 см, что более чем в 2 раза лучше ошибки базового расширенного фильтра Калмана ЕКЕ, комплексирующего входные данные GPS и лидарной локализации.

Результаты локализации АпКЕ (пороговый метод), АпКЕ (LOF) отличаются незначительно как показано на рис. 5. При этом АпКЕ (TCN) показывает более точную и шумную локализацию, чем АпКЕ (пороговый метод) и АпКЕ (LOF).

6.    Заключение

В настоящей статье детально исследован предложенный подход АпКЕ к локализации транспортного средства, обеспечивающий работу с различными современными алгоритмами детекции аномалий. В частности, рассматривались условия проезда автомобиля под туннелем, когда источник данных на основе GPS выдает недостоверную информацию. В АпКЕ по многомерным временным рядам от систем лидарной и GPS локализации происходит детекция аномалий и затем данные, предсказанные как достоверные, подаются в расширенный фильтр Калмана.

Созданный на основе симулятора CARLA набор данных позволил провести количественные эксперименты с предложенным подходом в разных дорожных ситуациях (при старте автомобиля внутри туннеля, при старте вне туннеля, но с полным проездом под туннелем и др.).

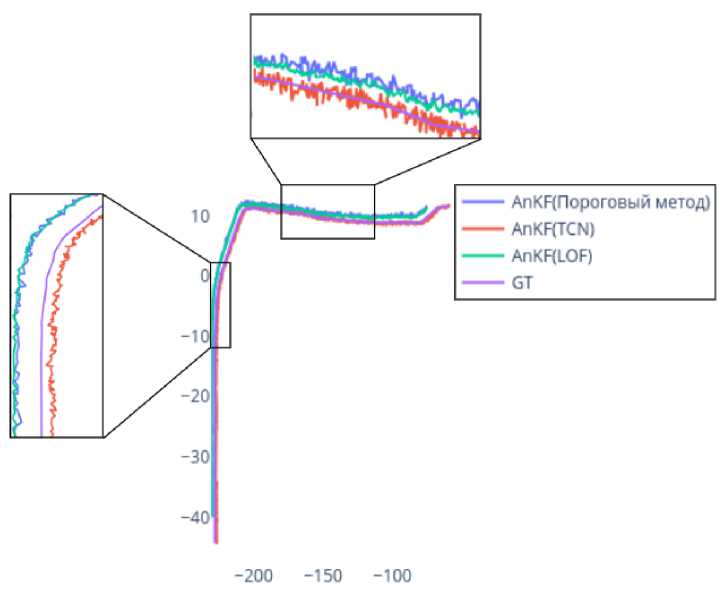
Рис. 5. Пример локализации транспортного средства, с помощью подходов AnKF (пороговый метод), AnKF (LOF), AnKF (TCN)

Было выявлено, что нейросетевые алгоритмы (TCN, RNN) более качественно обнаруживают аномалии, чем классические обучаемые подходы. Это подтверждается как значениями метрик полноты и точности классификации, так и оценкой качества, локализации после детекции аномалий.

Было показано, что применение предложенного необучаемого порогового алгоритма, детекции аномалий в составе подхода, комплексирования AnKF позволило по метрике качества. локализации превзойти большинство классических обучаемых моделей детекции аномалий (FB, HBOS, IForest, KNN, РСА). Это свидетельствует о потенциале разработки специализированных аналитических алгоритмов для задач комплексирования навигационных данных.

В дальнейшем предложенный подход можно расширить и на. другие источники навигационных данных, например, на. использование результатов локализации транспортного средства по данным бортовых камер или радаров.

В настоящей работе использовалась заранее построенная статическая карта, для локализации по лидарным облакам точек, то есть она. не обновлялась при изменении окружающей среды. Перспективным является исследование возможности обновления карты, что позволит актуализировать информацию о местности (дорожные работы, строительство новых сооружений) и может улучшить как лидарную локализацию, так и итоговое качество локализации предложенного подхода.

Работа, выполнена, при поддержке Аналитического центра, при Правительстве Российской Федерации в соответствии с договором о субсидии (идентификатор договора. 000000D730321P5Q0002; грант № 70-2021-00138).