Детектирование пиков наномасштабных изображений в шумах

В последнее время значительно расширился круг задач, решаемых с помощью анализа изображений самых различных объектов в области криминалистики, биологии, медицины, микроэлектроники, фармацевтики, аналитической химии и в других приложениях. В работе [1] предложены новые подходы анализа химического состава поверхности гетерогенных образцов, названные "химическая визуализация" (chemical imaging). В основе лежит анализ корреляции между, как минимум, двумя изображениями, полученными различными методами, например время-пролетной вторичной ионной масс-спектрометрией (ToF-SIMS) и сканирующей электронной микроскопией (SEM), рентгеновской фотоэлектронной спектроскопией и атомной силовой микроскопией (AFM) и т. п. с последующей обработкой многомерных данных [2–4].

Концепция многосенсорного гиперспектрального образа анализируемого объекта объединяет неразрушающие методы анализа на основе рамановской (RMS), энергодисперсионной рентгеновской (EDX) и электронно-колебательной спектроскопии, а также SEM и ToF-SIMS. Полученные изображения обрабатываются методами многомерной статистики для получения обобщенных спектральных признаков с использованием методов главных компонент (PCA) и кластерного анализа. Эта концепция находит применение в области науки о жизни, материаловедения и геофизики, классификации клеток и аэрозолей в пробах окружающей среды [1].

Одной из задач, решаемых в теории обработки изображений, является получение данных о морфологии поверхности, например морфологии на- ноструктур, используемых в различных приложениях от распознавания отпечатков пальцев и диагностики печатных плат [5] до оценки шероховатости поверхности [6–8], определения размеров наночастиц [9] и качества биосимуляров в фармацевтической промышленности [10].

Достоверность принимаемых решений по оценке морфологических параметров, в частности наноструктур, зависит от точности оценок этих параметров в условиях сильных шумов и других помех. Настоящая работа посвящена оценке интенсивности и положения пиков изображений, характерных для комплексных исследований с использованием атомной силовой, туннельной или растровой электронной микроскопии.

Традиционный подход в анализе структуры поверхности при наличии шумов основан на предварительной фильтрации шума с использованием тех или иных хорошо известных алгоритмов. Однако эта операция неизбежно ведет к искажению характера поверхности — нарушению формы пиков, уменьшению их интенсивности и иногда положения максимумов. В предлагаемом алгоритме не требуется предварительная фильтрация. Он основан на методе поиска начала, максимума и конца пиков по производной в трех точках скользящего окна данных, предложенного в работе [11]. Поиск максимумов изображения нанообъектов выполняется в два этапа. На первом — путем обнаружения экстремумов по строкам и столбцам матрицы данных формируются кластеры точек в зоне вершины пика. Затем, используя иерархический кластерный анализ, локализуются эти кластеры и определяются их центры, величина и расположение которых принимаются за параметры пиков в изображении.

ОПИСАНИЕ АЛГОРИТМА

Изображение, содержащее множество пиков, может быть представлено в виде матрицы Z, элементы которой z ( i,j ) определяются формулой

L

z (i, j)=Ё Af ((i - ii), (j - ji))+p( i, j), i=1

где A _l — интенсивность; f l — функция формы; i l , j l — положение l -го пика; L — число пиков; p^ij ) — аддитивный шум; i = 1 _ I , j = 1 _ J .

В простейшем случае в качестве модели функции fl может быть выбран двумерный гаусс fl (.) = Ai exP

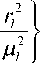
где r ² = ( i - i l ) 2 + ( j - j _i ) 2 , p _i — среднеквадратическая ширина пика.

В настоящей работе для проверки алгоритма используется более сложная модель пика, представляющая собой гауссов пик с эллипсоидальной формой сечения горизонтальной плоскостью. Тогда

r2 = ((i - ii) + (j - j i) )/Al -

^- в^ ( ( i - i ) cos ^a i

^-( j ^- Ji ) ^{sin a} i ) 2 1A ².

Здесь 2µ — фокальное расстояние и 2β — большая полуось эллипса, в/ > Ц/, ai — угол наклона оси эллипса в плоскости (i, j),

A i =7 ^{р 2} - ^ ² .

Каждый j- й столбец матрицы Z образует I -мерный вектор-столбец Z j = [ z_j ( i ) ] с элементами z j ( i ) .

Каждая i- я строка матрицы Z образует J -мерный вектор-строку Z i = [ z i ( j ) ] с элементами z - ^{( j} ) .

Алгоритм обнаружения положения ( i , j ) и амплитуды A пиков изображения производится последовательной обработкой по столбцам и строкам матрицы Z с последующим анализом полученных данных с целью уточнения искомых параметров.

При обработке по столбцам Z j производится поиск перегибов (хребтов) в каждом столбце j матрицы Z. Для этой цели используется подход, подробно изложенный в работе [11] для одномерного случая. Суть предлагаемого алгоритма состоит в следующем.

Сформируем текущую выборку у из K +1 отсчетов с центром в точке i вектора Z j у = [ y(k)] = (zj(i- K2),-, zj(i),-, zj(i+ K2)), где k = 1_ K и K выбирается всегда четным числом из условия 0.5–0.7 от ширины пика на половине высоты в отсчетах. При этом во избежание скачков на границах Z j полагаем, что если (i - K/2)< 0, то у (i - K/2) = Z J (1) и, если (i + KI2)> I, то у (i + KI2) = Zj(I).

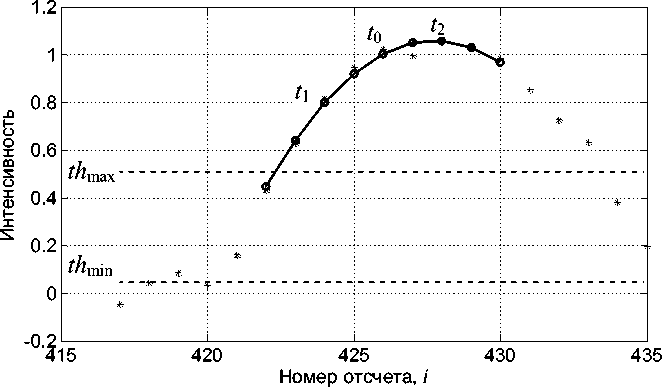
Рис. 1. Фрагмент столбца матрицы изображений с окном данных из девяти отсчетов ( K = 8) и аппроксимирующая парабола (сплошная линия) с точками t 1 , t 0 , t 2 ; th min , th max — минимальный и максимальный пороги обнаружения

Аппроксимируем отсчеты в окне y полиномом второй степени (параболой) у на сетке к = ( - К/ 2,...,0,..., К/ 2 ) :

у ( к ) = Р 1 к ² + p 2 к + p 3 ,

где p ₁ , p ₂ , p ₃ — коэффициенты полинома.

Выберем в интервале

такие, что t 1 = -

K

KK 2^,2

1 0 = 0, 1 2 =

три точки t ₁ , t ₀ , t ₂

K

, где

K

целое число, большее или равное .

На рис. 1 показан фрагмент столбца с окном данных из девяти отсчетов ( К = 8 ) и аппроксими-

рующая парабола с точками t ₁ , t ₀ , t ₂ .

Величина первой производной параболы в точке t ₁ будет равна

^d 1 = ² Р 1 t 1 ⁺ Р 2

и в точке t ₂ :

d 2 = 2 p 1 1 2 + p 2 .

Величина второй производной параболы равна 2 p ₁ .

Величина параболы в точке к = 0 равна средневзвешенному значению в скользящей выборке исходных данных в точке i :

Z j ( i ) = у ( 0 ) = p з .                       (3)

Используя формулы (1)–(3) рассмотрим алгоритм обнаружения хребтов в каждом столбце матрицы Z. В начале обработки исходных данных устанавливаются признаки обнаружения начала и вершины хребта:

р$ | 0, начало хребта необнаружено;

[ 1, начало обнаружено.

J 0, вершина хребта не обнаружена;

PSS 1,аршина^нааажана

Условие начала хребта имеет вид :

PS = 0; d 1 >  0; d 2 >  d 1 ; p 3 >  th min ,        (6)

где th _min — порог нижнего уровня, выбираемого по стандартному отклонению шума σ : ^th min = ( 1 ^ ² ^ .

После обнаружения начала хребта устанавливаются признаки PS = 1 и PSS = 0.

Обозначим номера строк, в которых обнаружены начала хребтов, как I _minmax.

Условие вершины хребта имеет вид :

PS = 1; d, > 0; d2 < 0; p, < 0; max (у )> th (7) 1 2 1 max где thmax — порог максимального уровня, выбираемый из условия thmax = (4 ^ 6)^ . После обнаружения вершины хребта устанавливаются признаки PS = 0 и PSS = 1. Обозначим номера строк, в которых обнаружены максимумы хребтов, как Imax .

Сформируем новую матрицу Z _m данных, состоящую из столбцов матрицы Z и строк с номера^ми I max , т. е. Z m = ^Z( I max , ^{1 J} )•

Выполним анализ матрицы Z _m по строкам I _max с использованием алгоритмов (4)–(7) с целью обнаружения номеров столбцов J _max , в которых обнаружены максимумы.

В результате приведенного анализа матрицы данных Z получаем координаты пиков в виде таблицы [ I max J max ] .

Амплитуда A ( I _max, J _max ) обнаруженных пиков оценивается по точке максимума параболы при условии PSS = 1. Если форма пиков несимметричная, то в окрестности их вершины даже при отсутствии шума обнаруживается несколько максимумов, образующих кластер. За оценку положения такого пика принимается среднее взвешенное значение по каждой координате, а за интенсивность — максимальное значение интенсивности пиков, входящих в кластер. Признаком принадлежности кластеру принимается расстояние между точками, которое должно быть меньше минимального расстояния между пиками анализируемой поверхности, задаваемого по априорным данным. За оценку положения кластера принимается среднее взвешенное значение по каждой координате, а за интенсивность — максимальное значение интенсивности пиков, входящих в кластер.

МОДЕЛИРОВАНИЕ

Проверка эффективности алгоритма производилась по модельному спектру, состоящему из 81 пика гауссовой формы с эллипсоидальной формой сечения и добавлением белого шума (рис. 2, а). На рис. 2, б, показаны кластеры пиков изображения и их вершины, полученные на основе предлагаемого

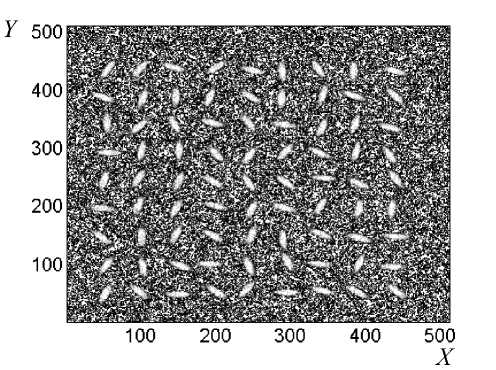
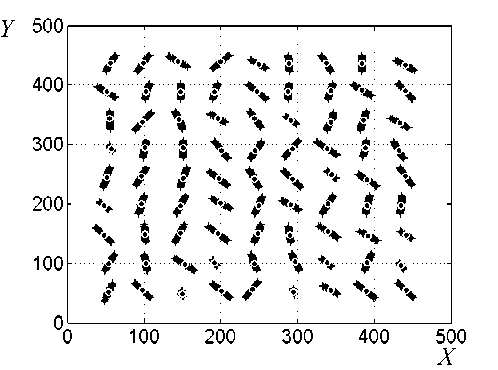
Рис. 2. Изображение из 81 модельных пиков.

а — в шумах при отношении сигнал/шум, равном трем; б — кластеры пиков изображения с отметкой обнаруженных вершин пиков (O)

Абсолютные (для положения пиков по осям X и Y ) и относительные среднеквадратические ошибки (СКО) оценки параметров пиков при различных отношениях сигнал / шум (с/ш) для метода поиска экстремумов, изложенного в [12, 13], — 1 и предлагаемого метода — 2.

Параметр Отношение с/ш 3.0 10 20 100 Метод поиска экстремумов 1 2 1 2 1 2 1 2 Положение пика (в отсчетах): X Y 0 1 0 1 0 1 0 0 0 0.8 0 0 0 0 0 0 Положение пика (СКО): X Y 1.65 1.51 0.85 1.13 1.44 1.38 0.97 0.87 1.40 1.33 0.9 0.68 1.40 1.30 0.90 0.60 Амплитуда 0.15 0.075 0.12 0.029 0.120 0.021 0.120 0.020 Вероятность правильного обнаружения 0.907 0.931 0.976 0.999 0.970 1 0.986 1 Вероятность ложного обнаружения 0.727 0.034 0.028 0.002 0.020 0 0.013 0 алгоритма. Результаты сравнивались с программой определения экстремумов в изображении — extrema2. m, используемой в разложении по эмпирическим модам (BEMD) [12, 13], с предварительной фильтрацией шума на основе мультивейвлетов [14]. Относительная погрешность оценки координат и амплитуды пиков производилась по десяти реализациям шума. Погрешность положения пика определялась по его отклонению от истинного значения. Максимальные значения погрешностей для обоих методов обработки сведены в таблицу.

Кроме того, вычислялась вероятность правильного обнаружения как отношение числа обнаруженных пиков по всем десяти реализациям, положение которых отличается от заданных в модели не более, чем на четыре отсчета, к общему числу модельных пиков. Вероятность ложного обнаружения вычислялась как отношение числа обнаруженных пиков по всем десяти реализациям, не заданных в модели, к общему числу модельных пиков. Сравнение данных в столбцах методов 1 и 2 таблицы показывает явное преимущество предлагаемого алгоритма как по уровню погрешности оценки параметров пиков, так и по величине вероятности ложного обнаружения.

ЗАКЛЮЧЕНИЕ

Алгоритм детектирования предложенным методом позволяет повысить достоверность обнаружения пиков благодаря низкому уровню ошибки оценок и вероятности ложного обнаружения при малых отношениях сигнал/шум. Это позволяет значительно понизить порог чувствительности приборов и расширить диапазон оцениваемых параметров.

Работа поддержана государственным заданием № 007-00229-18-00.