Детерминированный подход к решению задачи определения координат и угловой ориентации бортовой пеленгаторной антенны по результатам радиопеленгования радиоориентиров
Автор: Тяпкин В.Н., Виноградов А.Д.
Журнал: Журнал Сибирского федерального университета. Серия: Техника и технологии @technologies-sfu
Статья в выпуске: 3 т.13, 2020 года.
Бесплатный доступ
В работе рассматривается исследование возможности и условий однозначного определения координат и угловой ориентации бортовой пеленгаторной антенны (БПА), размещенной на подвижном объекте, по результатам азимутально-угломестного радиопеленгования радиоориентиров. Координаты подвижного объекта определяют по результатам измерений в одной или нескольких точках приема на борту подвижного объекта времен задержки радиосигналов, синхронно излучаемых не менее чем тремя радиоориентирами, а однозначная угловая ориентация в пространстве - путем измерения углов визирования не менее трех радиоориентиров не менее чем двумя пеленгационными парами точек приема с пересекающимися (неколлинеарными) базами. В статье приведены математические особенности определения пространственного положения БПА, общий подход к решению задачи при азимутально-угломестном радиопеленговании трех радиоориентиров, способы определения дальности до радиоориентиров по результатам их азимутально-угломестного радиопеленгования и анализ результатов исследования.
Азимутально-угломестный радиопеленг, радиоориентир, бортовая пеленгаторная антенна, навигационный приемник, источник радиоизлучения
Короткий адрес: https://sciup.org/146281594
IDR: 146281594 | УДК: 629.7.05 | DOI: 10.17516/1999-494X-0222
Текст научной статьи Детерминированный подход к решению задачи определения координат и угловой ориентации бортовой пеленгаторной антенны по результатам радиопеленгования радиоориентиров
Цитирование: Тяпкин, В.Н. Детерминированный подход к решению задачи определения координат и угловой ориентации бортовой пеленгаторной антенны по результатам радиопеленгования радиоориентиров / В.Н. Тяпкин, А.Д. Виноградов // Журн. Сиб. федер. ун-та. Техника и технологии, 2020. 13(3). С. 289-310. DOI: 10.17516/1999-494X-0222
гационную пару точек приема, и направлением на радиоориентир, проходящим через одну из точек приема пеленгационной пары, координаты которой определены вышеупомянутым образом [2, 4, 5]. То есть координаты и угловая ориентация подвижных объектов определяются спутниковыми радионавигационными системами дальномерно-угломерным методом, реализуемым при условии синхронного излучения радиосигналов радиоориентиров.
В известных работах по радионавигации [6-10] исследованы различные способы определения координат в пространстве подвижного объекта угломерным методом путем радиопеленгования с борта подвижного объекта, оснащенного бортовыми автономными навигационными датчиками и системами (инерциальными, геомагнитными) [11–14], радиоориентиром, реализуемым без предъявления требований к синхронности излучения радиосигналов радиоориентирами. Однако возможности одновременного и однозначного определения координат и угловой ориентации в пространстве подвижного объекта путем азимутально-угломестного радиопеленгования (определения азимута и угла места источников радиоизлучения) с борта подвижного объекта радиоориентиров без использования вспомогательной информации от автономных навигационных датчиков и систем в известных работах по радионавигации [1–14] не исследованы. При этом возникает необходимость решения задачи определения условий однозначности определения координат и угловой ориентации в пространстве подвижного объекта, оснащенного БПА, определяющих минимально возможное число и ограничения на взаимное пространственное расположение БПА и радиоориентиров.
Цель работы – исследование возможности и условий однозначного определения координат и угловой ориентации бортовой пеленгаторной антенны, размещенной на подвижном объекте, по результатам азимутально-угломестного радиопеленгования радиоориентиров.
Постановка задачи. Будем считать, что N радиоориентиров размещены в i-х точках Mi пространства (где i = 1,2,...,N) с известными координатами Mi(xi, yi, zi) в нормальной земной системе координат (НЗСК) Енз = {O, X, Y, Z}, представляющей собой левую пространственную прямоугольную декартовую систему координат, начало O которой фиксировано по отношению к Земле, ось абсцисс OX которой, находящаяся в горизонтальной плоскости, совпадает с северным направлением истинного или магнитного меридиана или вертикальной линии координатной сетки плоской прямоугольной геодезической системы координат, ось аппликат OZ которой перпендикулярна горизонтальной плоскости и направлена вверх по вертикали, а ось ординат OY которой, находящаяся в горизонтальной плоскости XOY, дополняет систему до левой пространственной прямоугольной декартовой системы координат [15]. Отсчет углов (азимута α и угла места ε) при азимутально-угломестном радиопеленговании реперных ИРИ с борта подвижного объекта, на котором размещена БПА, осуществляется в связанной системе координат БПА Есв = {O', X', Y', Z'}, представляющей собой левую пространственную прямоугольную декартовую систему координат, начало O' которой помещено в фазовом центре (ФЦ) БПА, осями которой служат продольная, поперечная и нормальная осевые линии БПА, являющиеся осями абсцисс O X , ординат O Y и аппликат O Z соответственно [16]. При этом азимут α представляет собой угол между проекцией направления от ФЦ БПА на радиоориентир на азимутальную плоскость O X Y , содержащую продольную и поперечную осевые линии БПА, и положительным направлением продольной осевой линии O X БПА, измеряемый в градусах в пределах от 0° до 360° и отсчитываемый от положительного направления продольной осевой – 291 – линии O'X' БПА по ходу часовой стрелки, если смотреть в направлении навстречу положительному направлению нормальной осевой линии O'Z' БПА. Угол места ε есть угол между направлением от ФЦ БПА на радиоориентир и проекцией вышеупомянутого направления на азимутальную плоскость O'X'Y', содержащую продольную и поперечную осевые линии БПА, измеряемый в градусах в пределах от 0° до ±90°, отсчитываемый от вышеупомянутой проекции на азимутальную плоскость O'X'Y' с положительным или отрицательным знаками в случае, если радиоориентир находится соответственно выше или ниже азимутальной плоскости O'X'Y', проходящей через ФЦ БПА.
Пространственное положение и угловую ориентацию БПА в НЗСК Енз = { О , X , Y, Z } будем характеризовать: во-первых, координатами x , у и z точки M 0 ( x , у, z ) размещения ФЦ О' БПА в НЗСК Енз = {О , X , Y, Z }; во-вторых, тремя углами Эйлера [17]: углами курса ^ , тангажа д и крена 9 , определяющими угловую ориентацию продольной OX' , поперечной O'Y' и нормальной O'Z' осевых линий БПА в нормальной земной подвижной системе координат (НЗПСК) Ензп = { О' , X , Y, Z }, представляющей собой левую пространственную прямоугольную декарто-вую систему координат, начало O' которой помещено в ФЦ O' БПА, а оси абсцисс O'X , ординат O'Y и аппликат O'Z которой направлены так же, как и оси соответственно абсцисс OX , ординат OY и аппликат OZ НЗСК Енз = {О , X , Y, Z } [17-19]. При этом угол курса у БПА представляет собой угол между проекцией на горизонтальную плоскость OX'Y НЗПСК Ензп = { О' , X, Y, Z } положительного направления продольной осевой линии O'X' БПА и линией O'X , расположенной в горизонтальной плоскости OX'Y , проходящей через ФЦ O' БПА, принятой за начало отсчета, измеряемый в градусах в пределах от 0° до 360° и отсчитываемый от вышеупомянутой линии O'X по ходу часовой стрелки, если смотреть в направлении вниз по вертикали, проходящей через ФЦ O' БПА. Угол тангажа μ БПА есть угол между продольной осевой линией O'X' БПА и горизонтальной плоскостью OX'Y НЗПСК Ензп = { О' , X , Y, Z }, проходящей через ФЦ О' БПА, измеряемый в градусах в пределах от 0° до ±90°, отсчитываемый от горизонтальной плоскости OX'Y с положительным или отрицательным знаками в случае, если положительное направление продольной осевой линии O'X' БПА находится соответственно выше или ниже горизонтальной плоскости OX'Y. Угол крена 9 БПА представляет собой угол между поперечной осевой линией O'Y' БПА и осью ординат ОХ ^ смещенной НЗПСК !нзп w = { О' , Xv , ¥„, , Z }, представляющей собой НЗПСК, оси абсцисс O'XV и ординат O'YV которой смещены относительно осей соответственно абсцисс OX и ординат ОТ НЗПСК Ензп = { О' , X , Y, Z } в положение, при котором угол курса у БПА равен нулю. Угол крена 9 БПА измеряется в градусах в пределах от 0° до ±90° и отсчитывается от оси ординат O'YV смещенной НЗПСК Ензп v = { О' , Xv , Yv , Z } с положительным или отрицательным знаками в случае, если положительное направление оси ординат O'YV смещенной НЗПСК ЕНЗП|// = { О' , X », Y„ Z } совмещается с положительным направлением поперечной ^ ^ , ^
осевой линии O'Y' БПА поворотом вокруг продольной осевой линии O'X' БПА соответственно по ходу или против хода часовой стрелки, если смотреть в положительном направлении продольной осевой линии O'X' БПА.
При одновременном азимутально-угломестном радиопеленговании с борта подвижного объекта N радиоориентиров, размещенных в i-х точках пространства с известными координатами Mi(xi, yi, zi), можно получить соответствующую совокупность i-х пар азимутов ai и углов места si (где i = 1,2,...N). Так как пространственное положение и угловая ориентация БПА опре-– 292 – деляются шестью неизвестными параметрами (тремя координатами x, у и z и тремя углами у, ц и У), то для их однозначного определения необходимо измерять не менее шести параметров, какими в рамках рассматриваемой задачи являются не менее трех пар азимутов αi и углов места εi, получаемых, соответственно, в результате радиопеленгования радиоориентиров с их общим числом N ≥ 3. Детерминированный подход к решению задачи определения координат ФЦ БПА x, у, z и углов у, ц и У, определяющих угловую ориентацию БПА, по результатам измерений не менее трех пар азимутов αi и углов места εi при азимутально-угломестном радиопеленговании не менее трех радиоориентиров можно представить в виде четырехэтапной процедуры, этапы которой предназначены для решения следующих частных задач:
-
– нахождение совокупности расстояний от ФЦ БПА до радиоориентиров;
-
– определение областей пространства, в которых совокупность расстояний от ФЦ БПА до радиоориентиров однозначна;
-
– определение координат ФЦ БПА;
-
- нахождение матрицы вращения и связанных с нею углов Эйлера, определяющих угловую ориентацию в пространстве БПА.
Система уравнений связи между неизвестной совокупностью расстояний от ФЦ БПА до радиоориентиров и соответствующей совокупностью известных (измеряемых) угловых параметров, возникающая при решении первой частной задачи на первом этапе, является нелинейной. Поэтому при азимутально-угломестном радиопеленговании с борта подвижного объекта трех радиоориентиров в общем случае произвольного взаимного пространственного расположения БПА относительно радиоориентиров решение вышеупомянутой определенной системы уравнений относительно совокупности расстояний от ФЦ БПА до трех радиоориентиров неоднозначно и может включать от одного до четырех решений. При увеличении размерности системы уравнений путем азимутально-угломестного радиопеленгования более чем трех радиоориентиров система уравнений связи становится переопределенной, и, соответственно, в случае учета погрешностей измерений азимутов и углов места она перестает быть совместной. Применение для ее решения стандартного метода наименьших квадратов приводит к повышению степени уравнений и, соответственно, к существенному усложнению процедуры определения искомых параметров. Поэтому в данной работе рассматриваем два случая, когда возможен детерминированный подход к решению первой и второй частных задач нахождения однозначной совокупности расстояний от ФЦ БПА до радиоориентиров: а) в случае азимутально-угломестного радиопеленгования трех радиоориентиров, не находящихся на одной прямой линии, когда система уравнений связи между искомыми и измеряемыми параметрами является определенной; б) в случае азимутально-угломестного радиопеленгования четырех радиоориентиров, три из которых расположены на одной прямой линии, когда система уравнений связи между искомыми и измеряемыми параметрами является переопределенной и совместной. Задачи третьего и четвертого этапов стандартны для радионавигации подвижных объектов [6–10], поэтому для их решения не требуется разрабатывать специальных методов. Ключевыми оказываются именно первые два этапа решения вышеупомянутых первой и второй частных задач. Структура возможных решений соответствующих нелинейных систем уравнений связи между искомыми и измеряемыми параметрами оказывается сложной, включая большое число вырожденных случаев. Без понимания данных особенностей затруднительно строить эффек-– 293 – тивные вычислительные алгоритмы однозначного определения координат и угловой ориентации БПА, размещенной на подвижном объекте, по результатам азимутально-угломестного радиопеленгования радиоориентиров.
Общий подход к решению задачи при азимутально-угломестном радиопеленговании трех радиоориентиров. Если три радиоориентира размещены в точках M 1( x 1, y 1, z 1), M 2( x 2, y 2, z 2) и M 3 ( x 3 , y 3 , z 3 ) с заданными известными координатами, находящихся не на одной прямой линии, а ФЦ O' БПА, размещенной на подвижном объекте, – в точке M 0 с неизвестными координатами M 0 ( x , y , z ), то в общем случае указанные четыре точки в трехмерном пространстве образуют треугольную пирамиду, схематическое представление которой приведено на рис. 1, где кроме вышеупомянутых параметров обозначены: £ i - длина i -го бокового ребра M 0 M i треугольной пирамиды M 0 M 1 M 2 M 3; di j – длина ребра MiM j основания M 1 M 2 M 3 треугольной пирамиды M 0 M 1 M 2 M 3 ; а у = Z MM 0 M j - плоский угол при вершине M 0 между боковыми ребрами M 0 M i и M 0 M j треугольной пирамиды M 0 M 1 M 2 M 3; i = 1,2,3; j = 1,2,3; i < j . Пространственное положение точки M 0 размещения ФЦ O' БПА и точек M i размещения i -х радиоориентиров в НЗСК Σнз = { O , X , Y , Z } будем также характеризовать радиус-векторами r 0 = ( x 0, y 0, z 0) и r i = ( xi , yi , zi ) соответственно, где i = 1,2,3.
Допустим, что в результате одновременного азимутально-угломестного радиопеленгования i -х радиоориентиров с использованием БПА определены три пары азимутов α i и углов места εi . Тогда в связанной системе координат БПА Σсв = { O' , X' , Y' , Z' } можно определить три единичных вектора s св i направлений на i -е радиоориентиры в соответствии с соотношением
sCBi = (cos ai cos ei, sin ai cos £i, sin £i), (1) где i = 1,2,3.
С учетом (1) косинусы плоских углов cos α ij при вершине M 0 треугольной пирамиды M 0 M 1 M 2 M 3 (см. рис. 1) можно определить в соответствии с соотношением
C°saj =(8св;, ScBj) = cos ^i COS Ejcos (a - а) + sin ^sin Ej, (2) где 1 ≤ i < j ≤ 3.
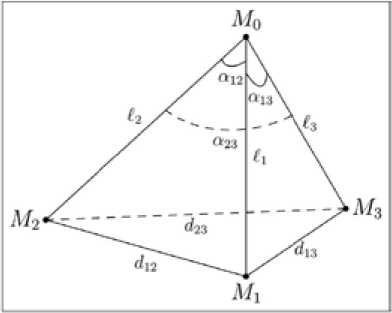
Рис. 1. Схема размещения в пространстве трех радиоориентиров и фазового центра БПА
Fig. 1. Spatial layout of three radio reference points and the onboard DF antenna phase center
Следует отметить, что длины d ij ребер MM основания M 1 M 2 M 3 треугольной пирамиды M 0 M 1 M 2 M 3 (см. рис. 1) являются априорно известными параметрами и определяются в соответствии с соотношением
2 22
dj
—
где 1 < i < j < 3.
С учетом известных значений вышеупомянутых параметров cos а 12, cos а 13, cos а 23, d 12, d 13 и d 23 для определения трех неизвестных значений длин £ , , £ 2 и £ 3 боковых ребер треугольной пирамиды MM 1 M 2 M 3 (см. рис. 1) получаем следующую систему из трех уравнений:
£2 + £2 - 2£,£ . cos^ . — d122;
Р2+£23 -2£1£ c- = d12з; (4)
22 2
'"2 + £3 - 2£2£.cos-.. = d23.
Как показали вычислительные эксперименты, система уравнений (4) относительно искомых значений параметров £ , , £ 2 и £ 3 может иметь от одного до четырех решений в каждой из двух областей пространства, находящихся симметрично относительно плоскости расположения трех радиоориентиров. Структура этих решений и правила выбора правильного (однозначного) решения будут описаны далее. Предположим, что однозначные значения параметров £ ъ £ 7, £з из системы уравнений (4) определены. Для неизвестных координат x , у и z точки 123
M 0 ( x , у, z ) расположения ФЦ БПА получаем следующую систему из трех уравнений:
г 2 2 2 2
( x - xj +( у -у,) + ( z - zj = £
й x - x 2 ) +(у - у 2 ) +( z - z 2 ) = £2; (5)l( x - x3)2 +(У - У3)2 +(z - z3)2 - £3-
Для решения системы уравнений (5) вычтем из второго и третьего уравнений первое уравнение и перенесем параметры, связанные с неизвестным значением z , в правые части уравнений, в результате чего относительно неизвестных значений координат x и у получаем следующую систему из двух уравнений:
-
2 x ( x - x 2 ) + 2 у ( у, - у 2 ) — £ 2 - £ х + x i - x 2 + у, - у 2 + z i - z 2 - 2 z ( z i - z 2 ) , (6)
-
12 x (x1 -x3)+2 у (у1- у 3)—£2- £2+x2 -x2+у-- у2+z1 -zl- 2z(Z1 - z3).
Согласно правилу Крамера решение системы уравнений (6) относительно координат x и у , зависящих от неизвестного значения координаты z , определяется соотношениями
x — VA(z) 2(у,-у2) у — V.,2(xi-x2) A(z), B(z) 2 (у1 у3) 2 (xi x3) B(z)
где
A (z)—12 - £2 + x, - x2 + у, - у2 + z; - z; -2 z (z,-z2);
B(z) — £2 - £2 + xi - x3 + у, - у3 + zi - z2 - 2z(zi - z3);
V – определитель системы уравнений (6), определяемый соотношением
V = 2
( x 1
( x 1
x 2 ) \ - x3 )
( y1 y 2 )
(y - У 3)
Для однозначной разрешимости системы уравнений (6) в соответствии с (7) требуется, чтобы определитель V системы уравнений (6) не был равен нулю, что с учетом (8) равносильно требованию того, чтобы точки M 1 ( xb yb z 1), M 2 ( x 2, y 2, z 2) и M 3 ( x 3, y 3, z 3) размещения радиоориентиров не находились на одной прямой, что напрямую вытекает из постановки задачи (см. рис. 1).
После подстановки соотношений (7) в одно из уравнений (5) получим квадратное уравнение относительно z . Полученное в результате решения вышеупомянутого квадратного уравнения значение координаты z точки M 0 ( x , y , z ) расположения ФЦ БПА используется в качестве известного параметра при решении системы их двух уравнений (6) в соответствии с соотношениями (7) относительно значений координат x и y точки M 0 ( x , y , z ) расположения ФЦ БПА.
После нахождения координат точки Mo (x, y, z) расположения ФЦ O БПА и вычисления в НЗСК Енз - {O, X, Y, Z} радиус-векторов r0 - (xо, yо, zо) и ri - (xi, yi, zi) можно определить три единичных вектора sнзпi направлений на i-е радиоориентиры относительно ФЦ O' БПА в НЗПСК !нзп - {O', X, Y, Z} в соответствии с соотношением s = S .5
нзп i нзп ix , нзп iy
r 0
r 0
rT
где S нзп ix , S нзп iy и S нзп iz — координаты i -го единичного вектора s^ i в НЗПСК 1 н., - { O' , X , Y, Z }; i - W.
Определим квадратную матрицу Sнзп размера 3×3 координат трех полученных по формуле (9) единичных векторов sнзп1, sнзп2 и sнзп3, записанных в столбцы, в соответствии с соотноше- нием тт
°нзп ( ’ нзпР э нзп2 ,
|
S нзп1 x |
s нзп2 x |
S нзп3 x |
|
s нзп1 y |
s нзп2 y |
s нзп3 y |
|
X S нзп1 z |
s нзп2 z |
S нзп3 z J |
где (∙)т – знак транспонирования.
По аналогии с (10) определим квадратную матрицу S св размера 3x3 координат трех полученных по формуле (1) единичных векторов S св1 , S св2 и S свз в связанной системе координат Есв - { O' , X' , Y' , Z' }, записанных в столбцы, в соответствии с соотношением
S ee = ( s Tei , » Тв2 . s T.3
Л cos«1 cos £1 sin a cos £
1 1
x sin £1
cos a cos £
sin a2 cos £2
cos a3 cos £3 Л
sin a 3 cos £ 3 . (11)
sin £2 sin £3
Квадратные матрицы Sнзп и Sсв размеров 3x3 связаны между собой матричным соотноше нием нзп
^ нзп Ч св ^св, нзп где qсв - квадратная матрица вращения размера 3*3 при переходе от связанной системы коор-
^Xг _ s—s ц;
-
■ z = sin Ц ;
^ YX = sin У cos ^ sin ц - cos S sin ^ ;
-
1 . у = cos S c O ^ ■ Sin S sin ^ Sin Ц ; (14)
'z =- Sin S cos ц ;
H z X = - sn S sin ^ - cos S cos ^ sin Ц ;
^ zY = sin S cos ^ - cos S sin ^ sin ц ;
^ zz = cosmos Ц .
По вычисленным значениям квадратных матриц S нзп и S св из формулы (12) получаем следующее соотношение для квадратной матрицы вращения ξ с н в зп размера 3×3:
Поскольку квадратная матрица вращения ξ нзп определена в соответствии с соотношением св
(15), то тем самым однозначно с использованием соотношений (15) определяют углы курса у, тангажа ц и крена 9 БПА. Например, угол тангажа ц определяют с использованием значения параметра 5 X z в виде ц = arcsin 5X - z , а углы курса у и крена 9 - с использованием значений параметров 5 хх , 5 xY , 5 v-z , 5 zz (если cos ц + 0) или значений параметров ^ v-z , 5 zх , 5 y'y , 5 zY (в противном случае).
Математические особенности определения пространственного положения БПА. Несмотря на внешнюю простоту системы уравнений (4), она имеет ряд особенностей, связанных с описанием всех ее решений относительно неизвестных значений параметров £1, £ 2 и £ 3 для разных случаев расположения в пространстве БПА и радиоориентиров, требующих обширного математического исследования. С прикладной точки зрения более практичным выглядит подход, заключающийся в разработке приближенного метода решения системы уравнений (4), учитывающего структуру возможных решений, полученную с использованием априорной информации относительно области возможных значений искомых параметров. Без понимания такой структуры возможных решений системы уравнений (4) гораздо сложнее разрабатывать – 297 – эффективные приближенные методы, позволяющие контролировать погрешности входных данных и промежуточных вычислений.
Систему трех уравнений (4) относительно трех неизвестных значений длин боковых ребер £ 1 , £ 2 и £ 3 треугольной пирамиды (см. рис. 1) можно свести в общем случае к уравнению четвертой степени относительно одной переменной. Для пояснения этой возможности необходимо указать на следующие свойства решений исходной системы уравнений (4).
Во-первых, если ( £ 1 , £ 2 , £ 3 ) - решение, то, очевидно, (- £ 1 , - £ 2 , - £ 3 ) тоже решение. Кроме того, хотя решение с отрицательными значениями ребер не «физично», оно оказывается связанным с аналогичной задачей для тех же точек Mb M 2, M 3 , но с набором углов а 12, a 13 и а 23 дающих те же значения по модулю косинусов. Например, если (- £ 1 , £ 2 , £ 3 ) - одно из решений для набора углов ( а 12 , а ц, а ) то ( „ £2, £ 3) - решение для углов ( , - а „, п - а 13 , а д).
Во-вторых, если считать все возможные решения, в том числе с нулевыми и отрицательными значениями длин боковых ребер £ 1 , £ 2 и £ 3, то их получится не более восьми. С учетом описанной выше симметрии количество положительных решений не превышает четырех.
В-третьих, каждое конкретное решение ( £ 1 , £ 2 , £ 3) непрерывно зависит от набора углов ( а 12 , а 13 , а 23 ).
В-четвертых, систему трех уравнений (4) относительно трех неизвестных значений длин боковых ребер £ 1 , £ 2 и £ 3 треугольной пирамиды M0M 1 M 2 M 3 (см. рис. 1) можно интерпретировать следующим образом. В каждой из боковых треугольных граней M0M i M j треугольной пирамиды MM 1 M 2 M 3 известна длина d j стороны MM треугольника и угол a ij , находящийся напротив указанной стороны MM , где 1 < i < j < 3. Следовательно, для каждой из боковых треугольных граней M-MM известен и соответствующий радиус R d окружности, описанной около боковой грани M 0 MM , причем отрезок MM , являющийся хордой окружности, делит окружность на две дуги, имеющие в общем случае разные длины. Искомая точка M о треугольной пирамиды M0M 1 M 2 M 3 (см. рис. 1) в зависимости от величины угла a ij , который может быть острым или тупым, может располагаться соответственно на большей или меньшей дуге окруж-
, - МММ и к ности, описанной около боковой грани MoMM. Для каждой из трех боковых треугольных граней M0MiMj вышепомянутая окружность не единственна и образует семейство окружностей, которое описывается как множество точек, находящихся на поверхности, образованной вращением окружности с радиусом R вокруг оси MiMj, лежащей в плоскости этой окружности dij i j и в отличие от обычного («открытого») тора пересекающей ее. При этом центр окружности, описанной около боковой грани M0MiMj, вращаемой вокруг оси MM, описывает окружность с центром в середине стороны MM основания MM2M3 треугольной пирамиды MM1M2Mз и d2
радиусом, меньшим, чем R d , и равным RR]-- i ^. Поэтому вышеупомянутая поверхность 4
представляет собой «закрытый» тор (тор без отверстия в центре), часть внешних границ которого, образованная вращением меньшей дуги окружности с радиусом Rd , располагается вну-ij три его внешних границ, образованных вращением большей дуги окружности с радиусом Rdj. Внешний вид «закрытого» тора, образованного вращением окружности с радиусом Rd вокруг оси MiMj, являющейся хордой окружности, представлен на рис. 2.
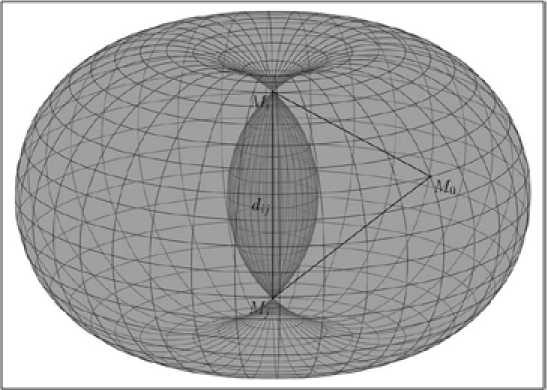
Рис. 2. Внешний вид «закрытого» тора, образованного вращением окружности вокруг ее хорды
Fig. 2. The external view of a “closed” torus formed by the rotation of a circle around its chord
Используя вышеупомянутую геометрическую интерпретацию особенностей описания возможных решений системы уравнений (4) относительно трех неизвестных значений длин боковых ребер £1, £2 и £3 треугольной пирамиды M0M1 M2M3 (см. рис. 1), можно составить эквивалентную системам уравнений (4) и (5) систему трех уравнений относительно трех неизвестных координат x, y и z точки M0 (x, y, z) расположения ФЦ БПА, обеспечивающую возможность определения координат ФЦ БПА без необходимости определения длин боковых ребер £1, £2 и £3 треугольной пирамиды. Для этого обозначим точками Mj (xj, yj, zj) середины ребер MM основания M1M2M3 треугольной пирамиды M0M1M2M3, координаты xij, yij и zij которых определяются в соответствии с соотношениями xij
+ x. y. + y. z. + z.
j ij ij
У; yj = 2; zj =
,
где 1 ≤ i < j ≤ 3.
Тогда систему трех уравнений относительно трех неизвестных координат x , y и z точки M 0 ( x , y , z ) расположения ФЦ БПА можно представить в виде
/ \2 / X2 / X2 d 12 I \2 / \2\ ,2 . 2
l( x - x,2 ) + ( y - y,2 ) + (z -Z12 )I -(( x - x12 ) +( y - y12 ) ) d12ctg «12 = 0;
2?
^ [ ( x - X 13 ) 2 + ( y - У 13 ) ’ + ( Z - Z 13 ) 2 - -4^ | - ( ( x - X 13 ) 2 + ( y - У 13 ) ’ ) d 12 ctg 2 « 13 = 0; (17)
-
2 A2
|l-x - -.^-y-'+'-z.)' - dr)-»----)"y-.nd 23-2--•
Для определения областей пространства, в которых совокупность расстояний £1, £2 и £3 от ФЦ БПА до трех радиоориентиров является однозначной, рассмотрим схему размещения в пространстве трех радиоориентиров и фазового центра БПА, приведенную на рис.1. Исходя из геометрического представления задачи нахождения трех неизвестных значений длин боковых ребер £1, £2 и £3 треугольной пирамиды M0M1M2M3, можно утверждать, что если каждый угол aij боковой грани M0MM больше соответствующего ему угла основания ЛM ,M kM j, 1 < k + i, j < 3, то решение единственно, а проекция точки M0 (x, y, z) расположения ФЦ БПА на плоскость треугольника M 1 M2M3 находится внутри треугольника основания M 1 M2M3. В случае, когда угол аи боковой грани MMMj оказывается равным соответствующему ему углу основа-
Jjuz i j нияЛ MiMkMj,возникает решение с нулевым ребром. При уменьшении угла aij боковой грани MoMiMj (например, при вертикальном подъеме БПА относительно плоскости треугольника MiM2Mз), в силу непрерывности, все значения боковых ребер £ь £ 2 и £ 3 треугольной пирамиды MMiM2M3 являются ненулевыми и положительными.
Особенности нахождения аналитического решения системы уравнений (4) относительно искомых значений параметров £ 1 , £ 2 и £ 3 продемонстрируем на основе частного случая, когда основание M1 M 2 M 3 треугольной пирамиды M 0 M 1 M 2 M 3 (см. рис. 1) представляет собой равносторонний треугольник со стороной d = d 12 = d 13 = d 23. Заметим, что используемые при этом приемы в целом применимы и для общего случая. При условии d = d 12 = d 13 = d 23 и замены переменных £ 2 = b £ 1 , £ 3 = С £ 1 (случай £ 1 = 0 следует рассмотреть отдельно) система уравнений (4) примет вид 222
£ 1 ( 1 2 b cos ^ 12 + b j — d ; , 2/ „ 2ч 2,
1 13 ; (Sl
(c2 - 2 bc cos^23+b2) — d2.
Если разделить первое уравнение системы (18) на второе, далее из суммы первого и второго уравнения вычесть третье уравнение системы (18) и, наконец, результат поделить на первое уравнение системы (18), то относительно двух неизвестных параметров b и c получим следующую систему из двух уравнений:
b2 - 2bcosa12 — c2 -2ccosa13; 2c(bcosа23 - cosa13) — b2 -1.
Из второго уравнения системы уравнений (19) выразим параметр c через неизвестный параметр b (случай b = ±1 требует отдельного рассмотрения), подставим полученное соотношение в первое уравнение системы уравнений (19) и относительно неизвестного параметра b получим уравнение
( 1 - 4cos2 а ) b 4 + 4cos a ( cos a + 2cos a , cos a ) b 3 - 2 ( 1 + 8cos a cos a cos a ) b 2 + ... ^ 23 23 23 12 23 12 13 23
^ ... + 4cos a 13 ( cos a 23 + 2cos a 12 cos a 13 ) b + 1 - 4cos2 a 13 — 0.
Для уравнения (20) значения угла а23, при которых cosа23 — 2, являются особыми. При таких значениях угла а23 порядок уравнения (20) понижается с четырех до трех. Кроме того, значения корня b = ±1 приводят к другим частным случаям. Эти обстоятельства не позволяют в общем случае использовать уравнение (20) для численного решения исходной системы уравне-– 300 – ний (18), поскольку при приближении к вышеупомянутым вырожденным случаям нарушается устойчивость искомых решений.
Следует отметить, что можно существенно упростить решение системы уравнений (5) путем введения локальной системы координат (ЛСК) Ел = {O", X" , Y”, Z" }, представляющей собой левую пространственную прямоугольную декартовую систему координат, начало O'' которой находится в точке пересечения медиан основания M 1 M 2 M 3 треугольной пирамиды M 0 M 1 M 2 M 3 , координаты xO", yO" и zO" которой в НЗСК Енз = { O , X , Y, Z } определяются соотношениями ось абсцисс OX которой, находящаяся в плоскости основания M 1 M2M 3 треугольной пирамиды M 0 M 1 M 2 M 3, проходит через точку M 1 размещения первого радиоориентира, ось аппликат O Z которой перпендикулярна плоскости основания M 1 M 2 M 3 с положительным направлением, образующим острый угол с осью аппликат OZ НЗСК !нз = {O , X , Y, Z }, а ось ординат O"Y" которой, находящаяся в плоскости основания M i M 2 M 3 треугольной пирамиды MMM 2 M з , дополняет систему до левой пространственной прямоугольной декартовой системы координат.
xO"
x + x 2 + x 3 _y , + y 2 + y 3
; ; yO- - ; ; zO"
z 1 + z 2 + z 3 3
Пусть r O- = ( x O‘ , yO " , zOA - радиус-вектор точки O" в НЗСК Енз = {O , X , Y, Z }, а вектор нормали n к плоскости треугольника M 1 M 2 M 3 определяется следующим образом:
n -( r 2 — r l )X( r 3 — r l )
s нз 1 s нз2 s нз3
x2 - Х1 У 2 - У1 z 2 - zl x3 — xl У 3 — У1 z3 — zl
где s нз1 = (1,0,0), S н з2 = (0,1,0), s нз3 = (0,0,1) - единичные орты в НЗСК. Если угол между положительными направлениями вектора нормали n и единичного орта s нз3 превышает 90°, то есть для скалярного произведения выполняется соотношение n • s нз3< 0, то вектор n заменяется на - n .
Определим единичные орты s л1, s л2 и s л3 ЛСК 1л = { O'\ X'' , Y'' , Z'' } в виде следующих соотношений:
s л1
JL-r^- s = s ”l х s лз s =Д I r . - Гс\ S л 2 Ьл! X s лз| ’ SЛ3 П .
Отметим, что порядок сомножителей в векторном произведении s × s , определяющем лл в соответствии с (23) единичный орт sл2, выбран таким образом, чтобы упорядоченная совокупность единичных ортов sл1, sл2 и sл3 ЛСК 1л = {O", X", Y", Z"} образовывала левую тройку векторов.
Пусть r - радиус вектор точки M0 расположения ФЦ БПА, имеющей координаты (x, y, z) в НЗСК и координаты (x'', y'', z'') в ЛСК. Тогда с учетом (21)-(23) справедливо векторное соотношение r - xSH3l + ySH32 + zSH33 - rO- + x''sл1 + y''sл2 + z''sл3" (24)
Из векторного соотношения (24) с учетом (21)-(23) можно получить следующие соотношения для определения координат ( x , y , z ) точки M 0 в НЗСК по полученным (заданным) значениям координат ( x" , y" , z" ) этой же точки в ЛСК:
|
X = хо. |
+ X " ( S л' |
■ S„1 ) + y" Ул 2 |
S H31 ) + z ''( s л3 |
S h3 ' ) ; |
|
y = Уо- |
+ s + X ( S л' |
S„ 2 ) + I’" ( S „2 |
S H32 ) + z ' ,( S л3 |
\ ■ S H32 ) |
|
. z = zo |
+ X - ( S л' |
S h33 ) + y '' ( S л2 |
S h33 ) + z" ( S л3 |
S h33 ) , |
и следующие соотношения для определения координат ( х'', y”, z” ) точки M 0 в ЛСК по полученным (заданным) значениям координат ( х , y, z ) этой же точки в НЗСК:
[ x " = ( X — x O -X ^ -' ) + ( y — У о -X S H32 - S "H z — Z O ^ S "33 ' S"
j y • = ( X - X ) ( S h S „ ) + ( y - Уо . ) ( S„2 - S „ ) + ( .- -^ ) ( S„ 3 ■ S ,2 ) ; (26) . Z ■ = ( X - X O ) ( Sh„ . S .3 ) + ( y - У о .) ( s„ 2 . s. ,3 ) + ( Z - Z o •) ( S„ 3 ■ S .3 ) .
Пространственное положение точек M i размещения i -х радиоориентиров в вышеупомянутой ЛСК Е л = {O", X”, Y" , Z" } будем характеризовать радиус-векторами r i = ( x", y", 0 ) , находящимися в плоскости основания M 1 M 2 M 3 треугольной пирамиды M 0 M 1 M 2 M 3, где i = 1,2,3. Тогда с учетом (25) и (26) и определенности выбора положительного направления оси абсцисс O"X" ЛСК Е л = {O", X", Y", Z" }, проходящего через точку M 1 размещения первого радиоориентира, при котором y . = 0 , система уравнений (5) для неизвестных координат х", y" и z" точки M 0 ( х", y'', z” ) расположения ФЦ БПА в ЛСК Е л = {O", X", У", Z" } может быть представлена в виде
( х ?x j+(, y 1 1 . < 2.
- ( x x 2) + ( y y2 .) + ( z ) ; (27 )
( X ■- X 3 ') 2 + ( y ■- y 3 ) 2 + ( z ) = < 2 .
При этом система из двух уравнений относительно неизвестных значений координат x'' и у точки M . расположения ФЦБПА в ЛСК O X, Г. Z- } полученная аналогичным об разом, как и система уравнений (6), с учетом (27) может быть представлена в виде
2 X ( х . - х 2 ) - 2 y"y 2 = 6 2 - 6 2 + () - ( х 2 ) 2 - ( y 2 ) 2 ;
2. X ( х .- х 3 ') - 2 y-y 3 = < 2 - < 2 + ( х . ) 2 - ( х 3 ) - ( y . ') 2 .
Согласно правилу Крамера решение системы уравнений (28) относительно координат х" и y" точки M0 расположения ФЦ БПА в ЛСК, в отличие от (7) не зависящее от неизвестного значения координаты z'', определяется соотношениями х"
A л - 2 y
_________ B л -2 y 3 __________. „
; y
2 ( y 2 ( X 1 - X 3 )- y 3 ( X 1 - X 2 ) )
2 ( х .- х 2 ) А .
______ 2 ( х .- х 3 ) B . (29) 2 ( y 2 ( х .- х , ■ ) - y 3 ( х .- X 2 ) ) , 2 ’
где
А л = < 2 - < 2 + ( X ,") 2 - ( X 2 ) 2 - ( y 2 ) 2, B л = 6 23 - 6 2 + ( X '- ) = - ( X 3 ) 2 - ( y 3- ) 2.
Из первого уравнения системы (27) с учетом полученных в соответствии с (29) значений x" и у" неизвестное значение координаты z" точки M 0 ( x" , у" , z" ) расположения ФЦ БПА в ЛСК !л = { O ", X", Y" , Z" } определяется в соответствии с соотношением
(z')2 = £2-( x'-x02-( у ) (30)
Определение координат ( x , у , z ) точки M 0 в НЗСК Енз = { O , X, Y, Z } по полученным в соответствии с (29) и (30) значениям координат ( x" , у" , z" ) этой же точки в ЛСК Е л = {O" , X'' , Y" , Z" } осуществляется в соответствии с соотношением (25).
Способы определения дальности до радиоориентиров по результатам их азимутально-угломестного радиопеленгования. Решение системы уравнений (4) относительно неизвестных значений длин £ 1 , £ 2 и £ 3 боковых ребер треугольной пирамиды M0M 1 M 2 M 3 (см. рис. 1), соответствующих дальностям от БПА до радиоориентиров, с помощью прямых аналитических методов, как было сказано ранее, сводится к поиску корней многочлена четвертой степени, один из вариантов которого определяется соотношением (20). Коэффициент при старшей степени может быть малым или даже вырождаться, что является причиной неустойчивости поиска корней вышеупомянутого многочлена. Поэтому более удобным с практической точки зрения представляется применение приближенного метода решения. Будем использовать метод Ньютона для нелинейных систем [20]. Этот метод наиболее эффективен в случае, когда имеется априорно известное начальное приближение для искомого решения. Обратная матрица, возникающая при реализации метода Ньютона, выписывается явно. Нет никаких других операций над данными, кроме арифметических, поскольку значения cos ау вычисляют в соответствии с соотношением (2) один раз по результатам измерений азимутов αi и углов места εi при одновременном азимутально-угломестном радиопеленговании i -х радиоориентиров с использованием БПА. Для получения требуемой точности вычислений искомых значений длин £,, £9 и £, достаточно сделать 5-6 итераций. Это обеспечивает прове- 12 3
дение расчетов в режиме реального времени. Решение системы уравнений (4), как было ранее отмечено, не является однозначным. Вместе с тем в условиях наличия априорно известной информации о ранее упомянутых закономерностях и условиях возникновения паразитных решений можно заранее рассчитать рекомендуемые области размещения БПА относительно радиоориентиров, чтобы метод Ньютона при решении системы уравнений (4) относительно неизвестных значений параметров £ 1 , £ 2 и £ 3 сходился к истинным значениям искомых параметров.
Для решения системы уравнений (4) методом Ньютона представим ее в векторной форме с использованием вектора F ( L ) в виде соотношения
Обозначим через DF ( L ) квадратную матрицу размера 3 х 3, элементами которой являются
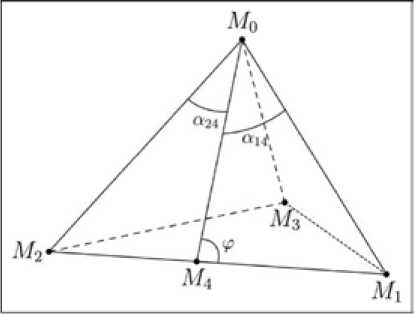
dF частные производные —- (где i = 1,2,3; j = 1,2,3) компонент Fi вектор-столбца F(L), определя-d емую с учетом (31) соотношением (А - t .cos a. 12 - t(cos «(2 0 ) DF(L) = 2 А( - А,cos«(, 0 А3 - А2^аи. (32) V 0 <2- А3cos«BА3 - <2cosa23 J Кроме того, обозначим через Lm) = (<(m) <(m) <(m) )твектор-столбец параметров Am>, <(2m>и Am>, соответствующих m-й итерации решения системы уравнений (4) методом Ньютона, где m = 0,1,2,^ - порядковый номер итерации. Тогда вектор-столбец L(m+(>=(l\m+(>,<2+(>, ^+(>)т дальностей от БПА до радиоориентиров <(m+(>, <2”+(>и I3m+(>, определяемых на (m + 1)-й итерации решения системы уравнений (4) методом Ньютона [20], с учетом (31) и (32) определяется соотношением -( L( -•“= L(- >-(DF (L( ->))F (L( ->), где (DF(L(m))) 1 - матрица, обратная матрице DF(L(m)), соответствующей m-й итерации решения системы уравнений (4), определяемая с учетом (32) соотношением - K 2 m> (m) K4 K(m) K4(m) K(m) - K<m>K(m> V 3 5 K(m) - K<m> K1(m)K5(m) K .., K4 .>, K(., Km > 2 3 / где K 1 1 2 (2 2 2 1 (2 K3m>= 2^3m>- 2^3m>cos a(3; K4m>= 2>- 2 <(m>cos a(3; K5m>= 2<(2->- 2 "> cosa,,; K6m>= 2<<m>- 2 m>cosa,,. При условии, что проекция ФЦ БПА на плоскость основания M1 M2M3 треугольной пирамиды M0M1M2M; находится внутри треугольника MiM2M3 и априорной неопределенности положения ФЦ БПА относительно радиоориентиров, в качестве «нулевой» итерации (m = 0) однозначного решения системы уравнений (4) методом Ньютона можно выбрать, например, вектор-столбец L(0>= р(0>, 1(0>, 1(0>) дальностей от точки O" пересечения медиан основания 123 M1 M2M3 треугольной пирамиды M0M1 M2M3 до точек M1 (x 1, у 1, z 1), M2 (x2, y2, z2) и M3 (x3, y3, z3) (0) размещения радиоориентиров, компоненты ti которого с учетом (21) определяются соотношением (0) 222 ^i = v(xi - xO') +(yi - yO") +(zi - zO") , (35) где i = 1,2,3. В последующем при периодически осуществляемом азимутально-угломестном радиопеленговании i-х радиоориентиров с использованием БПА и определением соответствующих i-м радиоориентирам азимутов ai и углов места Ei в качестве «нулевой» итерации (m = 0) одно-– 304 – значного решения системы уравнений (4) методом Ньютона в соответствии с соотношением (33) выбирается вектор-столбец L = ( 11,12,13)т дальностей от ФЦ БПА до точек M1(xbybz1), M2(x2,У2,z2) и M3(xз,У3,z3) размещения радиоориентиров, полученных по результатам предыдущего измерения азимутов αi и углов места εi радиоориентиров. Необходимо отметить, что при достижении определенной (критической) высоты h размещения ФЦ БПА относительно плоскости основания M1M2M3 треугольной пирамиды MM1M2M3 (см. рис. 1), зависящей от радиуса R окружности, описанной вокруг треугольника AM 1 M2M3, если проекция ФЦ БПА на плоскость основания M1M2M3 треугольной пирамиды M0M1M2M3 находится внутри треугольника AM1M2M3, появляется второе (ложное) решение системы уравнений (4), соответствующее расположению ФЦ БПА в одной из вершин треугольника AM1M2M3 (одно из значений длин боковых ребер £1, £ 2 и £ 3 треугольной пирамиды M0M1 M2M3 становится равным нулю). При дальнейшем увеличении высоты размещения ФЦ БПА относительно плоскости основания M1M2M3 треугольной пирамиды MM1M2M3 вышеупомянутое ложное решение системы уравнений (4) определяет положение ФЦ БПА, при котором высота размещения ФЦ БПА относительно плоскости основания M1M2M3 увеличивается, а проекция ФЦ БПА на плоскость основания M1M2M3 треугольной пирамиды MM1M2M3 находится вне треугольника AM1M2M3 и удаляется от вышеупомянутой вершины треугольника AM1M2M3. При достижении следующих критических высот появляются второе и третье аналогичные ложные решения системы уравнений (4), соответствующие положениям ФЦ БПА вблизи двух других вершин треугольника AM1 M2M3. При определенных симметриях вышеупомянутые ложные решения системы уравнений (4) могут появляться парой или даже тройкой. Это зависит от конфигурации треугольника AM1 M2M3, лежащего в основании треугольной пирамиды M0M1 M2M3, и г-ТТЛ траектории движения БПА. Необходимо отметить, что возможность однозначного решения системы уравнений (4) существует также и в случае, когда проекция ФЦ БПА на плоскость основания MiM2M3 треугольной пирамиды M0M1 M2M3 находится вне треугольника AM1 M2M3. Структура ложных решений системы уравнений (4), соответственно, также перестраивается. Задача полного описания решений системы уравнений (4) для всех возможных случаев представляется сложной и вряд ли реализуемой в наглядной и удобной для практического использования форме. Гораздо проще проводить расчеты по методике, предложенной выше, для заданной конфигурации размещения радиоориентиров и возможных траекторий движения БПА. Одним из других способов устранения неоднозначности решения системы уравнений (4) является использование результатов азимутально-угломестного радиопеленгования дополнительного четвертого радиоориентира. Размещение четвертого радиоориентира в произвольном положении относительно основания M1M2M3 треугольной пирамиды MаМ1M2M3 приводит к переопределенной системе уравнений относительно расстояний от ФЦ БПА до радиоориет-ниров. Фактически вместо одного треугольника в основании M1M2M3 треугольной пирамиды M0M1M2M3 при добавлении четвертого радиоориентира можно сформировать четыре треугольника. То есть можно определять неоднозначные решения от двух до четырех систем уравнений, аналогичных системе уравнений (4), и выбирать в качестве однозначного совместные решения. Однако с учетом погрешностей азимутально-угломестного радиопеленгования радиоориентиров этот вариант требует отдельного исследования. Вместе с тем, если дополнительный (чет-– 305 – вертый) радиоориентир будет располагаться на одном из ребер основания M1M2M3 треугольной пирамиды M0M1M2M3, то исходная задача однозначного решения системы уравнений (4) значительно упрощается – решение становится единственным и определяется в виде аналитических соотношений. Без ограничения общности будем считать, что точка M4(x4,y4,z4) с заданными известными координатами x4, y4 и z4 размещена на ребре M1M2 основания M1M2M3 треугольной пирамиды M0M1M2M3, что поясняется схемой точек M0, M1, M2, M3 и M4 размещения в пространстве соответственно фазового центра БПА и первого, второго, третьего и четвертого радиоориентиров, приведенной на рис. 3, где кроме ранее приведенных обозначений обозначено: a14 = ZM 1 M0M4 - плоский угол при вершине M0 между боковыми ребрами M0M1 и M0M4 треугольной пирамиды M0M1 M3M4; a24 = ZM2M0M4 - плоский угол при вершине M0 между боковыми ребрами M0M2 и M0M4 треугольной пирамиды M0M2M3M4; ф = ZMMm, - угол с вершиной в точке M4 между отрезками линий M4M0 и M4Mь раз-041 4 40 41 мещенными на боковой грани M0M1M2 треугольной пирамиды M0M1M2M3. Введем также обозначения отрезков d14 = M1M4 и d24 = M2M4 ребра M1M2 основания M1M2M3 треугольной пирамиды M0M1M2M3. Так как sin(π – φ) = sinφ, то из треугольников M0M4M1 и M0M4M2 по теореме синусов можно получить равенства 14 sin ai4 L d24 L —— и--24— = ——, из которых получаем следующее соотно-sin ф sin a24 sin ф шение: L1sin a14 _ L 2 sin a24 d = d 14 24 = sin Ф. Введем обозначение P = d24 sin ai4. d14sin a24 Тогда с учетом (36) и (37) получаем Рис. 3. Схема размещения в пространстве четырех радиоориентиров и фазового центра БПА Fig. 3. Spatial layout of four radio reference points and the onboard DF antenna phase center £ 2 = р£1. (38) В соответствии с теоремой косинусов для треугольника ΔM1M0M2 (см. рис. 1) получаем соотношение £2 - 2££2 cosа12 + £22 = d2. Из соотношения (39) с учетом (37) и (38) получаем следующую формулу для определения длины ребра £1 (см. рис. 1): £1 = d12 . 1 - 2pcosa7 + Р С использованием вычисленных по формулам (40) и (38) значений длин боковых ребер соответственно £1 и £2 треугольной пирамиды M0M1 M2M3 (см. рис. 1) для определения длины бокового ребра £ 3 треугольной пирамиды M0M1 M2M3 в системе уравнений (4) из третьего уравнения вычтем второе, в результате чего получаем следующее соотношение: £ 3 = 23 2 2 1 ^2 + w23 w13 2 (/1Cosa13 £ 2С0^а23) Анализ результатов исследования. Обоснование предложенных алгоритмов однозначного определения координат и угловой ориентации БПА, размещенной на подвижном объекте, по результатам азимутально-угломестного радиопеленгования минимально возможного числа радиоориентиров, равного трем, связано в первую очередь с необходимостью упрощения реализации размещения в пространстве системы радиоориентиров. При определении координат и угловой ориентации БПА, размещенной на подвижном объекте, по результатам азимутальноугломестного радиопеленгования более чем трех радиоориентиров в общем случае точность определения координат и угловой ориентации БПА повышается. Однако привлечение дополнительных радиоориентиров при решении поставленной задачи приводит к необходимости рассмотрения переопределенных несовместных нелинейных систем, что существенно усложняет поиск однозначного их решения относительно искомых параметров. Покажем, что небольшие погрешности измерений не приводят к несовместности системы уравнений (4). Это обстоятельство оказывается существенным, поскольку поставленную задачу решают в рамках детерминированной модели. Следовательно, можно обойтись без функционала ошибок, построение и изучение свойств которого в случае нелинейных систем является предметом дополнительного исследования. Для этого воспользуемся результатами, изложенными в пункте «Математические особенности определения пространственного положения БПА». На поверхности «закрытого» тора (см. рис. 2) один из плоских углов α12, α13 или α23 при вершине M0 треугольной пирамиды M0M1M2M3 (см. рис. 1) оказывается постоянным. Если перемещаться по линии пересечения двух таких «закрытых» торов, то два плоских угла при вершине M0 треугольной пирамиды M0M1M2M3 остаются постоянными, а третий меняется. Следовательно, имеется возможность построения пирамиды M0M1M2M3, соответствующей данным измерений плоских углов α12, α13 или α23 с малыми погрешностями путем поочередного изменения на небольшую величину измеряемых значений всех трех углов α12, α13 или α23 при вершине M0 треугольной пирамиды M0M1M2M3. Следовательно, си- стема уравнений (4) остается совместной, и для ее решения не требуется строить функционал ошибок. Когда число радиоориентиров больше трех и никакие три из них не находятся на одной прямой, с учетом полученных результатов исследования может быть предложена следующая процедура однозначного определения координат и угловой ориентации БПА, размещенной на подвижном объекте, по результатам азимутально-угломестного радиопеленгования радиоориентиров: во-первых, выбирют несколько троек радиоориентиров; во-вторых, для каждой выбранной тройки радиоориентиров решают систему уравнений (4) рассмотренными способами; в-третьих, полученные решения согласуют с помощью метода наименьших квадратов или простым усреднением. Построение процедуры «отбраковки» ложных решений, основанной на использовании дополнительной информации при одновременном азимутально-угломестном радиопеленговании более чем трех чисел радиоориентиров, требует дополнительного исследования. Более продуктивным выглядит подход, когда из имеющихся радиоориентиров в каждый момент времени для проведения измерений выбирают тройку радиоориентиров, пространственное положение которой относительно ФЦ БПА обеспечивает наибольшую точность измерений. При этом критерии оптимальности выбора тройки радиоориентиров следует формировать с учетом устойчивости проводимых расчетов. Для однозначного определения координат и угловой ориентации бортовой пеленгаторной антенны, размещенной на подвижном объекте, по результатам азимутально-угломестного радиопеленгования радиоориентиров предложена четырехэтапная процедура, включающая, во-первых, нахождение совокупности расстояний от фазового центра БПА до радиоориентиров; во-вторых, определение областей пространства, в которых совокупность расстояний от фазового центра БПА до радиоориентиров является однозначной; в-третьих, определение координат фазового центра БПА; в-четвертых, нахождение матрицы вращения и связанных с нею углов Эйлера, определяющих угловую ориентацию в пространстве БПА. Решение задачи нахождения совокупности расстояний от фазового центра БПА до радиоориентиров угломерным методом имеет сложную структуру. Аналитические методы определения совокупности расстояний от фазового центра БПА до радиоориентиров по результатам их азимутально-угломестного радиопеленгования с борта подвижного объекта возможны, но приводят к уравнениям высоких степеней с возможным вырождением порядков уравнений, что означает неустойчивость прямых методов их решения. По-видимому, возможно применение методов регуляризации, но это требует дополнительного математического обоснования. Поэтому предложен устойчивый численный метод решения задачи нахождения совокупности расстояний от фазового центра БПА до радиоориентиров угломерным методом, позволяющий в случае осуществления периодического азимутально-угломестного радиопеленгования с борта подвижного объекта трех радиоориентиров, расположенных в вершинах треугольника, однозначно определять координаты и угловую ориентацию бортовой пеленгаторной антенны, размещенной на подвижном объекте. Предложен вариант размещения в пространстве четырех радиоориентиров, три из них расположены на одной прямой, при котором решение задачи нахождения совокупности расстояний от фазового центра БПА до радиоориентиров на основе использования результатов их азимутально-угломестного радиопеленгования с борта подвижного объекта является единственным и определяется в виде аналитических соотношений.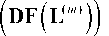
Список литературы Детерминированный подход к решению задачи определения координат и угловой ориентации бортовой пеленгаторной антенны по результатам радиопеленгования радиоориентиров
- Яценков В.С. Основы спутниковой навигации. Система GPS NAVSTAR и ГЛОНАСС. М.: Горячая линия - Телеком, 2005. 272 с.
- Тяпкин В.Н., Гарин Е.Н. Методы определения навигационных параметров подвижных средств с использованием спутниковой радионавигационной системы ГЛОНАСС: монография. Красноярск: Сибирский федеральный университет, 2012. 260 с.
- Пестряков В.Б. Радионавигационные угломерные системы. М.-Л.: Госэнергоиздат, 1955. 304 с.
- Перов А.И., Харисов В.Н. ГЛОНАСС. Принципы построения и функционирования. 4-е, перераб. и доп. изд-е. М.: Радиотехника, 2010. 800 с.
- Корнев В.В., Чмутин Н.Ф. Определение пространственной ориентации объекта в среде глобальных радионавигационных спутниковых систем. Ракетно-космическое приборостроение и информационные технологии. 2016. Сборник трудов VIII Всероссийской научно-технической конференции "Актуальные проблемы ракетно-космического приборостроения и информационных технологий" (1-3 июня 2016 г.). Под ред. д.т.н., профессора А.А. Романова. М.: АО РКС, 2016, с. 52-69.
- Белавин О.В. Основы радионавигации. Изд. 2-е, перераб. и доп. М.: Сов. радио, 1977. 320 с.
- Беляевский Л.С., Новиков В.С., Олянюк П.В. Основы радионавигации. М.: Транспорт, 1982. 288 с.
- Ярлыков М.С. Статистическая теория радионавигации. М.: Радио и связь, 1985. 344 с.
- Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации. М.: Радио и связь, 1992. 304 с.
- Бакулев П.А., Сосновский А.А. Радиолокационные и радионавигационные системы: М.: Радио и связь, 1994. 296 с.
- Бранец В.Н., Шмыглевский И.П. Введение в теорию бесплатформенных инерциальных навигационных систем. М.: Наука, 1992. 280 с.
- Алешин Б.С., Веремеенко К.К., Черноморский А.И. Ориентация и навигация подвижных объектов: современные информационные технологии. М.: ФИЗМАТЛИТ, 2006. 424 с.
- Виноградов А.Д., Востров А.Ю., Дмитриев И.С. Оценивание пространственной ориентации подвижного объекта по показаниям ортогональных акселерометра и магнитометра. Успехи современной радиоэлектроники, 2016, 7, 35-45.
- Чаплыгин А.А., Семенов Н.Н., Лукьянчиков В.Д., Медведев А.Б. Использование бортовых навигационных комплексов для решения задач в различных радиотехнических приложениях. Антенны, 2014, 9(208), 40-56.
- ГОСТ 22268-76 Геодезия. Термины и определения. M.: Издательство стандартов, 1977. 34 с.
- Виноградов А.Д., Востров А.Ю., Дмитриев И.С. Обобщенная структура радиопеленгатора и основные термины, используемые в теории радиопеленгования. Антенны, 2018, 5(249), 5-20.
- Ишлинский А.Ю. Ориентация, гироскопы и инерциальная навигация. М.: Наука, 1976. 622 с.
- ГОСТ Р 51794-2008. Глобальные навигационные спутниковые системы. Системы координат. Методы преобразования координат определяемых точек. M.: Стандартинформ, 2009. 16 с.
- ГОСТ 20058-80 Динамика летательных аппаратов в атмосфере. Термины, определения и обозначения. M.: Издательство стандартов, 1981. 56 с.
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.Г. Численные методы. Изд-е 8. М.: Лаборатория Базовых Знаний, 2000. 636 с.


