Development of a hydraulic damping device to protect a centrifugal pump

Бюллетень науки и практики / Bulletin of Science and Practice

UDC 62-752.2                                      

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №7. 2024

Hydraulic transmission exhibits superior characteristics, such as a high power density ratio and the ability to achieve endlessly variable speeds, when compared to mechanical transmission [1]. The hydraulic transmission device lacks intricate mechanical mechanisms, hence streamlining machinery design. Hydraulic devices have the ability to enhance the arrangement of the mechanical structure and enable the achievement of downsizing and the demands of contemporary mechanical design.

However, hydraulic technology itself is not without its share of challenges. Energy loss is the consequence of the stability and reliability of hydraulic transmission, which are the two primary elements of significance [2]. Hydraulic shock, also known as water hammer, occurs when there is a rapid and significant increase in liquid pressure within a hydraulic circuit. The maximum pressure frequently exceeds the standard operating pressure [3]. The presence of vibration and noise often coincides with incorrect action of certain hydraulic components, leading to equipment damage. This is commonly caused by loose hydraulic seals resulting in oil leakage, which hinders the proper functioning of the system. Additionally, the significant energy loss caused by vibration greatly impacts the stability, reliability, and economy of the system [4].

These issues are especially noticeable in large-scale industrial equipment. In the context of heavy industrial machinery, the intricate operational conditions lead to fluctuations in the load, which in turn generate significant variations in pressure inside the system. These pressure changes give rise to a substantial impact, ultimately leading to the instability of the entire system. Hence, accurately examining the hydraulic shock mechanism, mitigating the detrimental effects of hydraulic shock, and enhancing the hydraulic system's performance have significant importance [5].

The schematic diagram of the experimental setup is shown in Figure 1.

I

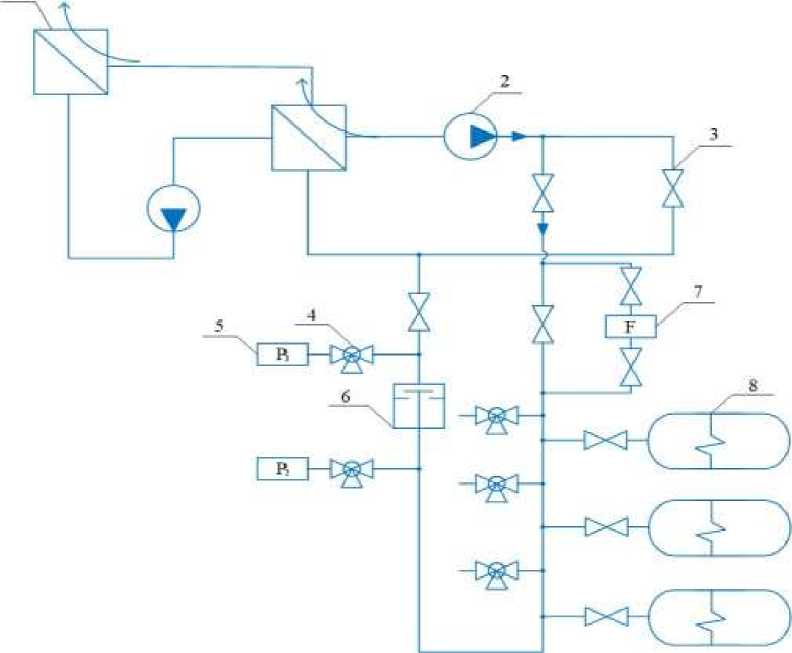
Figure 1. Scheme of the experimental setup. 1-Electric boiler Protherm (Proterm) SKAT 24K; 2-centrifugal pump; 3-check valve; 4-three-way valve; 5-pressure gauge; 6-shock valve; 7-flow meter;8-hudraulic accumulator

The water in the electric boiler flows into the pipeline via the valve. However, if the shock valve is abruptly closed, it can cause hydraulic shock across the entire experimental system. Currently, manipulate the valve located in front of the hydraulic buffer to either open or close it. By seeing and comparing the variations in pressure over time within the pipeline, you can effectively assess the hydraulic buffer's capacity to alleviate hydraulic shock.

The computer-linked sensors are utilized to retrieve the data from the pressure gauge and flow meter. Figure 2 displays the connecting diagram for the experimental setup.

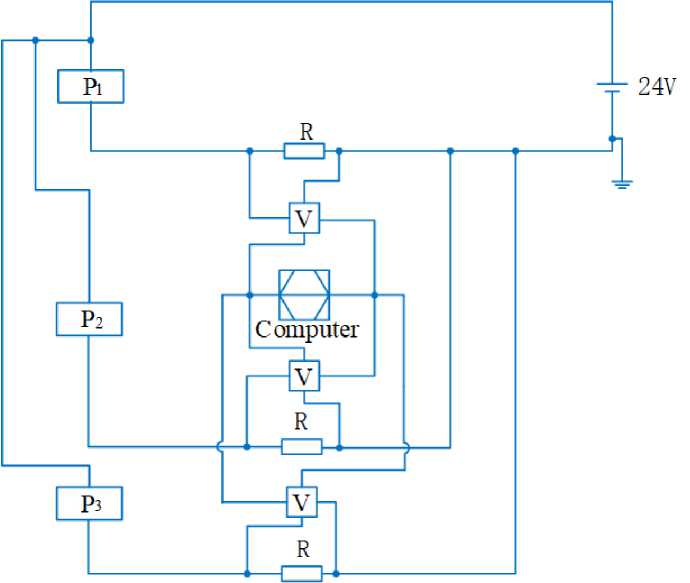
Figure 2. Sensors transmit and read experimental data

The experimental setup was established and investigated by placing the valve in front of the hydraulic accumulator in either the closed or open position. The experimental setup was checked to ensure that the experiment was implementable. The change in pressure over time was observed and recorded for various flow sizes utilizing the conducted experiment. The details regarding the experimental configuration are outlined below.

Experimental equipment information

Electric water heater, pump, hydraulic accumulators, digital to analog converter, pressure transmitter (transducer), flow meter were mainly used in the construction of the whole experiment.

The electric boiler is a wall-mounted, single circuit, electrically heated boiler for use in forced water circulation systems. Has an LCD display for showing temperature, operating mode and other parameters, as well as displaying fault codes. Cantilever pumps 80-50-200 (a) are designed for pumping water for industrial and technical purposes with pH from 6 to 9 (except for sea) and other liquids similar to water in density, viscosity and chemical activity in water supply, heating, and circulation systems. The size of solids is up to 0,2 mm with a volume concentration of no more than 0,1%. A digital-to-analog converter is an electronic circuit that converts any digital signal (such as a binary signal) into an analog signal (voltage or current). Designed for conversion of overpressure, overpressure-vacuum into standard (standardized) output signals of direct current or voltage in systems of automatic control, regulation and control of technological processes.

Specific information about the experimental equipment is shown in the Table 1-6 below:

EQUIPMENT INFORMATION ELECTRIC BOILER PROTHERM SKAT 24K

EQUIPMENT INFORMATION PUMPS-K 80-50-200A

Table 1

Installations	Number	Input Voltage/ V	F/ Hz	IP	Q/ kW	P/ kW	η	PMS/ bar	T max / т	V/ L
Electric boiler Protherm SKAT 24K	CC01320 741	3×230/400	50	40	24	23,9	99,50%	3	85	71

Table 2

Unit Name		K 80-50-200A
Nomin. Flow rate, m³/h	45
Nomin. Head, m	40
Work Area	Flow rate, m³/h	Head, m
	28...58	35... 44
Cavit. Stock, m	3.5
Electric motor**	stamp	Kw	rpm
	AIR 132M2	11	3000
	mm*
Overall dimensions of the unit	L	B	H
	990	440	425
	mm
Nozzle diameter, mm	entrance	exit
	80	50
Pump weight, kg*	56
Unit weight, kg*	172

• *    Dimensions and weights are for cast bed pumps. The dimensions and weight of the units on the welded frame differ to a lesser extent.

• * * The power of the electric motors for the energy-saving versions of the pumps is shown in parentheses, while the flow and head do not change.

  EQUIPMENT INFORMATION HYDRAULIC ACCUMULATORS

  
  

Table 3

Installations	Diamete r/ m	Pmax / bar	T max / °C	Scope	Weight/ kg	Volume/ L	Height / m	Connection
Diaphragm tank for hot water and solar systems WESTER Premium WDV 12 l 12 bar (stainless steel)	0,28	12	100	DHW, solar system s	2,39	12	0,307	Male thread 3/4"

Table 4

SPECIFICATIONS
ADC
Number of channels	16 differential or 32 with "common ground"
ADC Bit Depth	14 bit
Input Signal Measurement Sub-Ranges	±10 V; ±2,5 V; ±0,625 V; ±0,156V
Maximum Conversion Rate	400 kHz
Synchronization	1.Internal
2.From the sync signal,
3.By Analog Signal Level
Overload Immunity by Input Measurement Signal	±30 V (power on)
±10V (power off)
Cross-channel traversal	-78 dB (10 kHz sine wave)
Digital Signal Processor
Type	ADSP-2185M
Clock rate	48 MHz
Internal Data RAM	16 CZK
Internal RAM of programs	16 Kslov
FIFO Buffer ADC	512 - 12288 Words
FIFO DAC buffer	512 - 4032 Words
DAC (optional)
Number of Voltage Outputs with Common Ground	2
Bit width	12 bit
Establishment Time	8 μs
Output current, not more than	2 mA
Digital Inputs and Outputs
Number of inputs	16 (parallel, asynchronous)
Number of outputs	16 (parallel, asynchronous with common output resolution)
Logic type	TTL-Compatible
Digital Input Voltage Range	-0,2 to +0,6 V (logic zero)
+2,4...+5,0 V ("logical unit")
Voltage range at digital outputs	0...+0,4 V ("logical zero")
At least 2,4 V ("logical unit")
Output current per 1 TTL channel, max	±4 mA
Total power consumption from all outputs	0,5 W
(TTL, DAC, external power outputs), no more than
Powered by USB bus
Consumption current	Up to 400 mA
Dimensions: 140×96×30 mm. Weight: no more than 0,2 kg

DEVICE INFORMATION DIGITAL TO ANALOG CONVERTERS

Measured media: air, steam, liquids and other media neutral to the materials of the device in contact with the measured medium (stainless steel 12Kh18N10T, titanium alloy VT; sealing material-paronite for pressure up to 2,5 MPa, copper for pressure from 4 MPa and more; special rubber — for CRT 9 with an open membrane). Designed for conversion of overpressure, overpressure-vacuum into standard (standardized) output signals of direct current or voltage in systems of automatic control, regulation and control of technological processes.

DEVICE INFORMATION PRESSURE TRANSMITTER

Table 5

Insta llatio ns	Pressure   Basic    Out    Supply    Weight/ Enclosure   The temperature   Ambient air ranges/   error/ signal   voltage/      kg     protection of the measured is   temperature Mpa     %    / mA    DC A                        from/ °C        / °C
value	0-1,6    ±0,25;   4-20     9-30    not more    IP65;      -45°Cto+110°C         - ±0,5;                        than      IP67                         40°Cto+86 ±1                          0,175                                          °C

Table 6

EQUIPMENT INFORMATION - FLOW METERS

Installations	number	Q/ (m3/h)	P/ MPa	accurate
flow meter	015045114	0,020~5	1,6	0,2%-0,5%

Analysis and calculation of experimental data

The experiment was divided into two main parts. The first part is to close the valve in front of the hydraulic accumulator and observe the pressure changes before and after the impact valve at different flow rates (0,108 m3/h; 0,201 m3/h; 0,306 m3/h; 0,401 m3/h; 0,505 m3/h; 0,600 m3/h; 0,685 m3/h; 0,746 m3/h). The second part is to open the valve in front of the hydraulic accumulator, because the hydraulic accumulator has the ability to relieve the hydraulic shock, at this time to observe the pressure change before and after the shock valve at different flow rates (0,209 m3/h; 0,300 m3/h; 0,403 m3/h; 0,505 m3/h; 0,600 m3/h; 0,639 m3/h; 0,736 m3/h; 0,970 m3/h) (Figure 3).

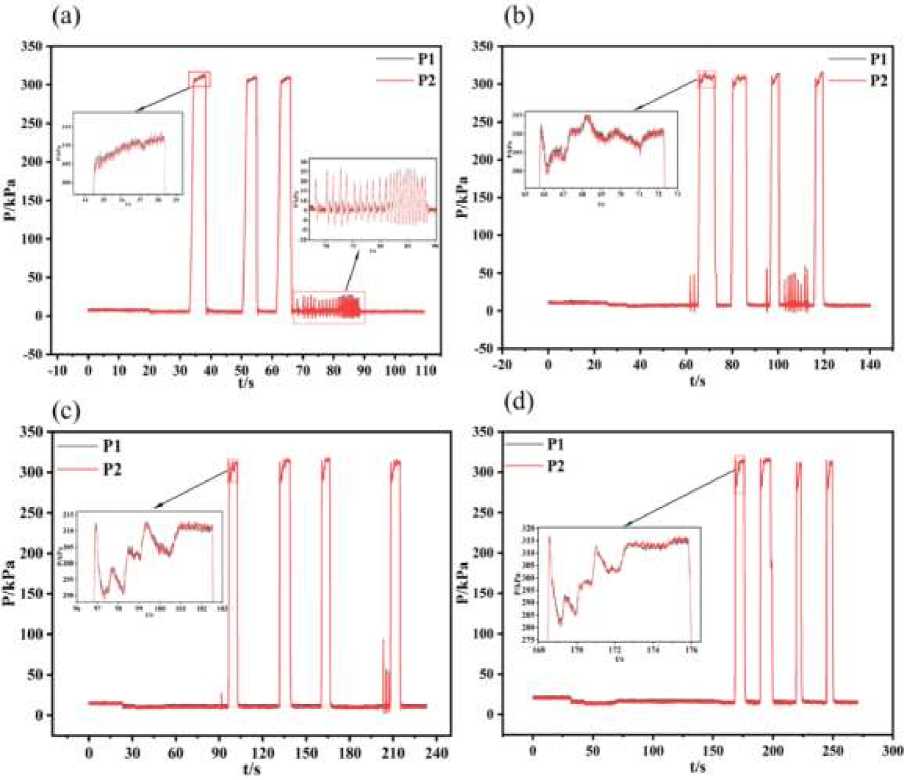
• Figure 3. Figure 3.

Figure 3 while the system is operating normally, abruptly closing the valve will result in a rapid and significant increase in pressure within the pipe, leading to a hydraulic shock. When the shock valve is closed for an extended duration, a rectangular picture will be observed in Figure 2 (a), accompanied by an increase in pressure amplitude. When the shock valve rapidly closes and then opens, it generates a disrupted signal known as a short wave. Upon observing the figure, it is evident that the pressure values at the front and back of the shock valve experience a substantial decrease when the break signal is detected. This indicates that the hydraulic shock that occurred earlier has been alleviated as a result of the valve opening correctly.

Figure 3 and Figure 4 Figure 4.d isplay superimposed fluctuations. The observed superimposed amplitudes in the pressure change images before and after the vibrating valve in a hydraulic shock are typically caused by the combined effects of the operational characteristics of the vibrating valve and the parameters of the oil line on the propagation of the pressure wave. The characteristics of shock valves, such as the duration of opening and shutting, as well as the force required to open them, have a direct impact on the shape and magnitude of the pressure wave. Simultaneously, the characteristics of the oil pipeline, including its length, pipe diameter, material, etc., will influence the pace at which pressure waves propagate, as well as their attenuation and reflection. Consequently, these factors will ultimately affect the amplitude of the pressure wave. Therefore, the presence of several pressure wave pictures with comparable amplitude can indicate the combined impact of the vibrating valve and the oil pipeline.

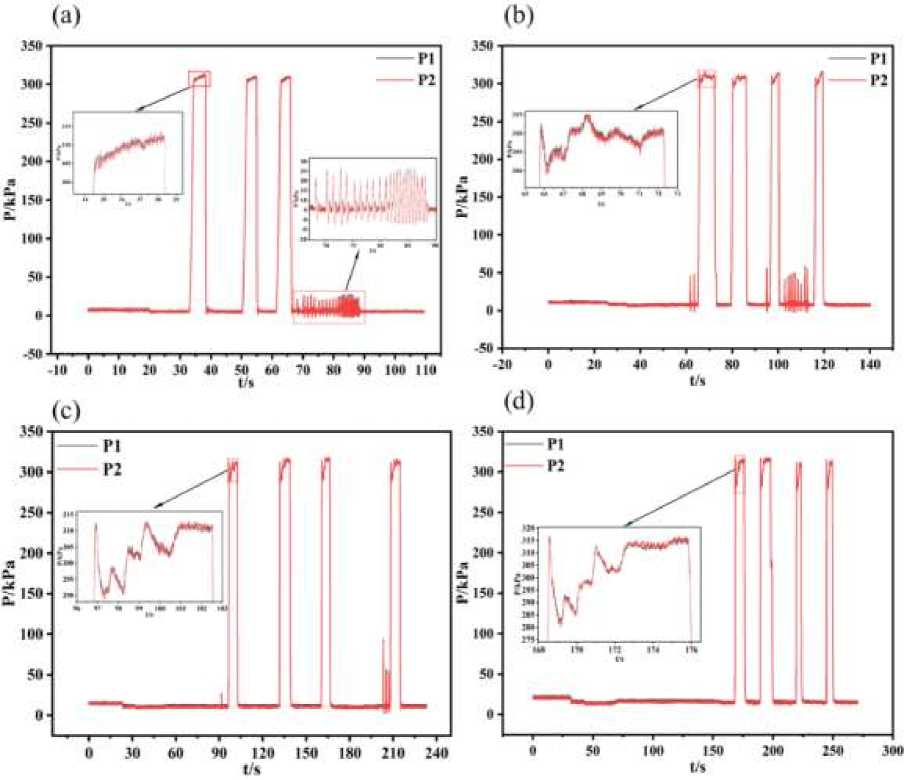
Figure 3. Trend of pressure change with time when the valve is suddenly closed. (a) Flow rate: 0,108 m3/h; (b) Flow rate: 0,201 m3/h; (c) Flow rate:0,306 m3/h; (d) Flow rate: 0,505 m3/h

Figure 3 and Figure 4 demonstrate that, aside from the overlaid variations, there is minimal disparity in pressure before and after the valve following certain duration subsequent to its abrupt closure. Despite the abrupt closure and subsequent reopening of the valve, the pressure differential before and after the valve remained minimal. This occurs due to the presence of inertia in the hydraulic system, which results in a relatively small pressure difference before and after the shock valve when it is abruptly closed or opened during a hydraulic shock. When a vibrating valve is abruptly shut, the fluid in the hydraulic system retains its inertia and generates a pressure wave that induces an immediate alteration in pressure as the wave spreads both ahead of and behind the valve.

By examining the localized enlargements in Figure 3 and Figure 4, it becomes evident that the oscillations in the top band of the chart exhibit a stepped pattern. The stepped peak band of the pressure wave is caused by the transient effect in the hydraulic system. When the shock valve is shut, the fluid in the hydraulic system generates a pressure wave that results in an immediate alteration in pressure. Due to the viscosity and inertia of the liquid, the pressure wave encounters resistance and reflection as it travels, leading to alterations in the form of the pressure wave.

As the wave travels from an area of high pressure to an area of low pressure, its speed drops, resulting in the waveform taking on an ascending step shape. As the wave travels from the area of low pressure to the area of high pressure, its velocity increases, resulting in the waveform taking on a descending step shape. Hence, the emergence of a step-like configuration in the pressure wave during a hydraulic shock is a result of a modification in the velocity at which the wave propagates.

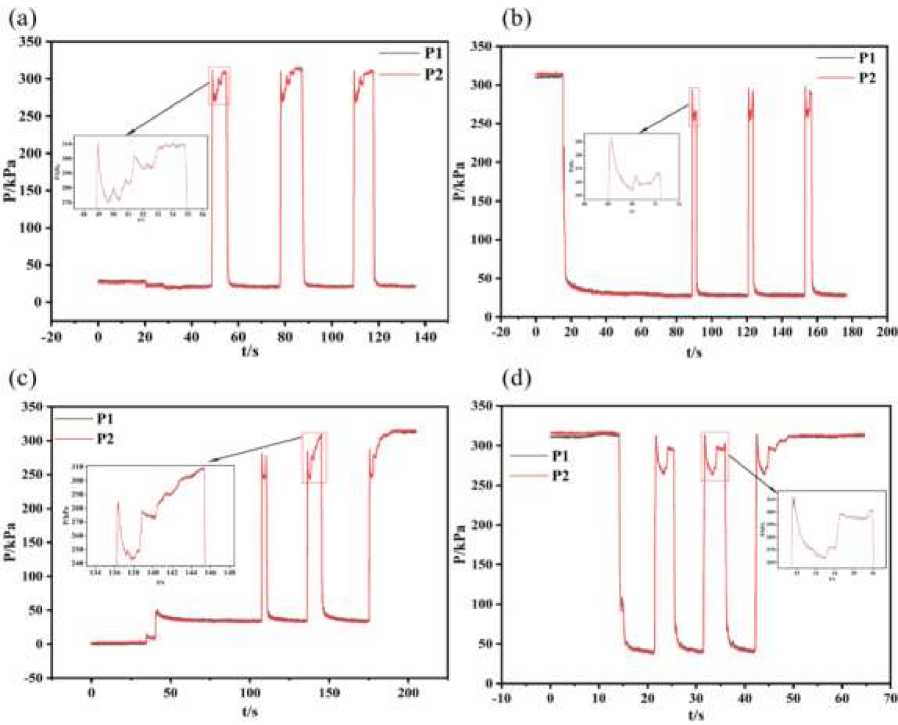
Figure 4. Trend of pressure change with time when the valve is suddenly closed. (a) Flow rate: 0,505 m3/h; (b) Flow rate: 0,600 m3/h; (c) Flow rate: 0,685 m3/h; (d) Flow rate: 0,746 m3/h

The experimental pipe is made of polypropylene and has an inner diameter of 16 mm and an outside diameter of 25 mm. During the analysis of the experimental data, it is necessary to determine the propagation speed of the hydraulic shock wave and draw a judgment regarding the required amount of damping. The shock propagation time is defined as the duration between the last pressure amplitude and the subsequent pressure amplitude. The velocity of propagation of the shock wave v [6]:

v = —( m/s )

Damping characteristic factor C [0] :

C = n dL ( pa • sm ²)

Damping factor D [7]:

D = CA ( N • s/m )                                        ⁽³⁾

Damping force F [0 -0] :

F = - Dv ( N )                                      (4)

Among them, L is the length of the pipe (m); t is the impact propagation time (s); h is the viscosity of the liquid, and the value taken here is 1,002×10^-3 Pa·s/m²; d is the inner diameter of the pipe (m), the nominal diameter of the Male thread 3/4” is DN20; A is the area of the effective surface of the action (m²).

Table 7

INITIAL CALCULATION PARAMETERS

Effective area/ m2	Fluid viscosity/ (Pa·s)	Length/ m	Inner diameter/ m	Effective damping coefficient C/ (Pa·s/m2)	Damping factor D/ (N·s/m)
0,0314	0,001	6	0,016	1869,775	58,71094

Observe the experimental data in the experimental process, select the valid data with small error for calculation can ensure the accuracy of the experiment [7].

The physical parameters of the fluid in the tube are shown in Table 7, combined with different flow rates in the tube and the transmission speed of the shock wave when the valve is suddenly closed, the damping value that needs to be increased when the valve is suddenly closed at different flow rates can be calculated. The following table shows the damping calculations for closing the valve at various flow rates:

Table 8

CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,108 m3/h

close-0,108	P1	P2
First maximum amplitude/ kPa	313,500	314,00
cyclicality/ s	16,440	16,030
velocity/ (m/s)	0,365	0,374
damping/ N	-21,429	-21,958
Second maximum amplitude/ kPa	311,000	311,500
cyclicality/ s	11,190	11,440
velocity/ (m/s)	0,536	0,524
damping/ N	-31,469	-30,765
Third maximum amplitude/ kPa	310,500	310,500

Table 9

CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,201 m3/h

close-0,201	P1	P2
First maximum amplitude/ kPa	315,000	315,500
cyclicality/ s	14,510	14,440
velocity/ (m/s)	0,414	0,416
damping/ N	-24,277	-24,395
Second maximum amplitude/ kPa	312,000	311,500
cyclicality/ s	16,880	17,030
velocity/ (m/s)	0,355	0,352
damping/ N	-20,869	-20,685
Third maximum amplitude/ kPa	314,000	314,500
Table 10 CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,306 m3/h
close-0,306	P1	P2
First maximum amplitude/ kPa	313,000	313,000
cyclicality/ s	36,740	36,830
velocity/ (m/s)	0,163	0,163
damping/ N	-9,588	-9,565
Second maximum amplitude/ kPa	316,000	317,000
cyclicality/ s	29,700	29,110
velocity/ (m/s)	0,202	0,206
damping/ N	-11,861	-12,101
Third maximum amplitude/ kPa	318,000	318,000
Table 11 CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,685 m3/h
close-0,685	P1	P2
First maximum amplitude/ kPa	281,500	281,500
cyclicality/ s	37,220	37,300
velocity/ (m/s)	0,161	0,161
damping/ N	-9,464	-9,444
Second maximum amplitude/ kPa	309,000	309,500
Table 12 CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,401 m3/h
close-0,401	P1	P2
First maximum amplitude/ kPa	317,000	317,000
cyclicality/ s	14,230	19,840
velocity/ (m/s)	0,422	0,302
damping/ N	-24,755	-17,755
Second maximum amplitude/ kPa	317,000	318,000
cyclicality/ s	55,270	54,010
velocity/ (m/s)	0,109	0,111
damping/ N	-6,374	-6,522
Third maximum amplitude/ kPa	314,500	314,500
Ifcc) ® Тип лицензии CC: Attribution 4.0 International (CC BY 4.0)		364

Бюллетень науки и практики / Bulletin of Science and Practice Т. 10. №7. 2024

Table 13

CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,505 m3/h

close-0,505	P1	P2
First maximum amplitude/ kPa	311,500	311,000
cyclicality/ s	35,660	30,900
velocity/ (m/s)	0,168	0,194
damping/ N	-9,878	-11,400
Second maximum amplitude/ kPa	314,500	315,500
cyclicality/ s	32,060	31,600
velocity/ (m/s)	0,187	0,190
damping/ N	-10,988	-11,148
Third maximum amplitude/ kPa	311,000	312,000
Table 14 CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,600 m3/h
close-0,600	P1	P2
First maximum amplitude/ kPa	294,000	291,000
cyclicality/ s	31,840	31,840
velocity/ (m/s)	0,188	0,188
damping/ N	-11,064	-11,064
Second maximum amplitude/ kPa	296,000	294,500
cyclicality/ s	32,460	32,460
velocity/ (m/s)	0,185	0,185
damping/ N	-10,852	-10,852
Third maximum amplitude/ kPa	298,000	296,000
Table 15 CALCULATION OF THE ADDITIONAL DAMPING REQUIRED FOR SUDDEN VALVE CLOSURE AT A FLOW RATE OF 0,746 m3/h
close-0,746	P1	P2
First maximum amplitude/ kPa	312,000	310,500
cyclicality/ s	10,040	10,140
velocity/ (m/s)	0,598	0,592
damping/ N	-35,086	-34,740
Second maximum amplitude/ kPa	313,000	310,500

By examining Tables 8-15 and comparing the damping values, it becomes evident that altering the flow rate in a hydraulic shock will impact both the timing of the pressure peak and the level of extra damping. As the velocity of flow increases, the greater inertia and kinetic energy lead to a reduced time for the pressure to reach its maximum, and also need higher damping to regulate the pressure peak. However, within a specific range, as the flow rate increases, the required quantity of damping does not necessarily increase proportionally, but rather exhibits a pattern of initially increasing and then decreasing. The reason for this is that when the flow rate increases, there is a corresponding rise in the inertia and kinetic energy of the fluid. This leads to an increase in the inertial damping of the fluid, which in turn results in better control of the pressure peak. Based on the analysis of the data provided, it is evident that the size and rise in damping in hydraulic impacts should be evaluated and computed individually for each specific scenario.

The necessary damping would differ across various conditions. The precise amount of additional damping needed depends on the matching flow rate, and the magnitude of the damping is displayed in Tables 8-15. It should be noted that the amplitudes used for the calculations vary based on the images generated from the experimental data. This is due to the fact that there is an instantaneous increase in pressure in front of the valve as the flow in the pipe continues to increase. Therefore, only two specific amplitudes were obtained for the calculations in Tables 14 and 15, which are now explained. It is evident that when the hydraulic accumulator is open, if the valve is abruptly closed while the hydraulic pressure is being relieved, the pressure in front of the valve (P2) will be higher than the pressure after the valve (P1). As the rate of flow in the tube increases, the difference in pressure between P2 and P1 also grows progressively. This phenomenon occurs when the valve is abruptly shut, causing the fluid in the pipeline to rapidly cease flowing and generate a backflow. This, in turn, triggers the formation of a pressure wave that travels towards the valve. The hydraulic accumulator's capacity to absorb energy causes the principal pressure wave to be directed towards it. Consequently, the pipe positioned before the hydraulic accumulator will experience high pressure, specifically in front of the valve.

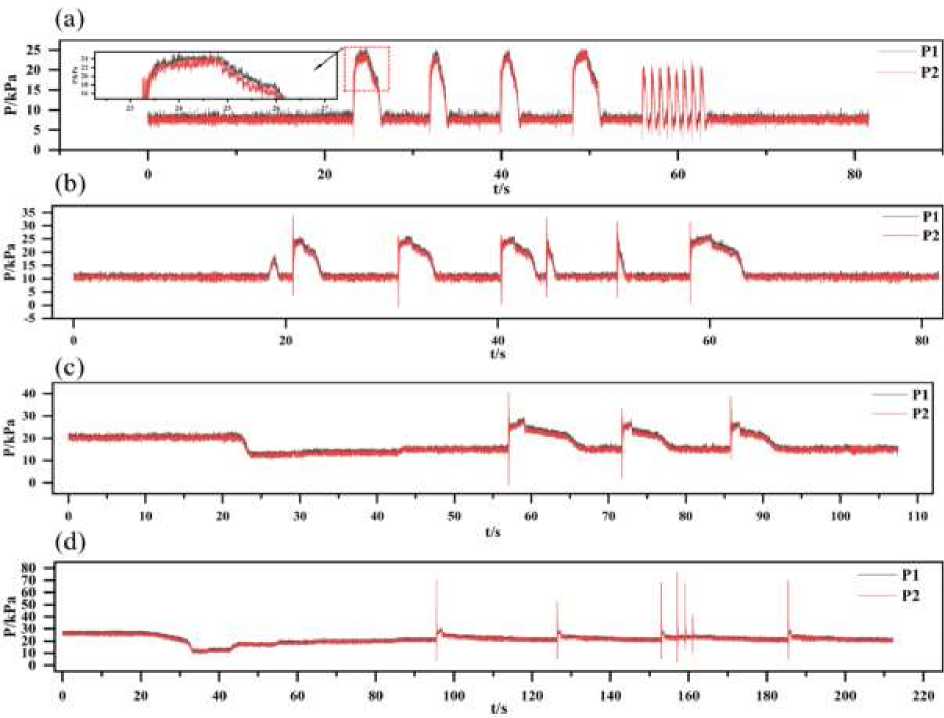
Figure 5. Trend of pressure with time when a hydraulic accumulator is opened and the valve is suddenly closed. (a) Flow rate: 0,209 m3/h; (b) Flow rate: 0,300 m3/h; (c) Flow rate: 0,403 m3/h; (d) Flow rate: 0,505 m3/h

However, when the flow rate in the tube increased to 0,970 m3/h, if the hydraulic accumulator is opened to release the hydraulic pressure and then the valve is abruptly closed, the pressure difference before and after the valve is not significant. This is because the hydraulic accumulator is able to absorb some of the energy. Here, the pressure wave generated by the reverse flow is directed towards the hydraulic accumulator upon valve closure.

The accumulator then absorbs this wave, resulting in a decrease in the pressure difference across the valve. Currently, the hydraulic accumulator is more effective in reducing pressure waves compared to inertia. When the flow rate reaches a certain level, the hydraulic accumulator can effectively mitigate most of the pressure wave, resulting in minimal pressure difference before and after the valve.

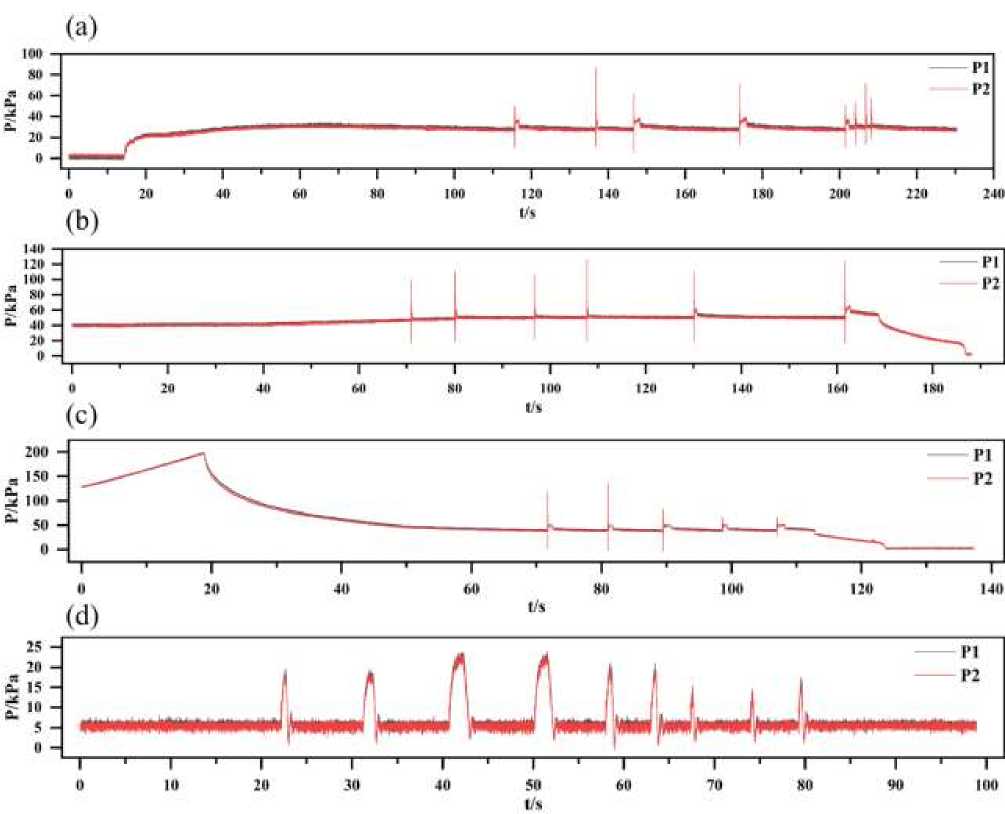
Figure 6. Trend of pressure with time when a hydraulic accumulator is opened and the valve is suddenly closed. (a) Flow rate is: 0,600 m3/h; (b) Flow rate is: 0,639 m3/h; (c) Flow rate is: 0,736 m3/h; (d) Flow rate is: 0,970 m3/h

Experiment results

Subsequent investigations confirmed that the utilization of hydraulic accumulators can effectively mitigate hydraulic shock in the system resulting from the inadvertent closure of the valve. During the analysis of the experimental data, it was discovered that the speed at which the hydraulic shock wave spreads is connected to the time interval between the last and next maximum amplitudes of the shock wave, when hydraulic buffers are not used. Nevertheless, there was no discernible association between the shock propagation time and the flow rate in the tube, even as the flow rate in the tube increased. This demonstrates that the speed at which a particular hydraulic shock wave spreads, when there is more resistance to its movement, must be evaluated individually for each situation.

The experimental data shows that the maximum damping force is 35,0864 N, and it occurs when the tube flow rate is 0,746 m3/h. Given that the overall maximum flow rate of the system is 0,746 m3/h, the hydraulic accumulator's capacity to reduce hydraulic pressure within the system is at least 35,0864 N, which meets the required criteria.

When the flow rate in the pipe changed between 0,108 m3/h and 0,403 m3/h, and 0,970 m3/h, the pressure without the hydraulic accumulator increased by approximately 270 kPa. This rise in pressure was aimed at safeguarding the system from hydraulic shocks. When the flow rate in the tube varied between 0,505 m3/h and 0,736 m3/h, the pressure without the hydraulic accumulator increased by approximately 100 kPa to 223 kPa.

Conclusion

The hydraulic accumulator in the hydraulic system continuously fills and discharges fluid to convert the pressure energy in the system and reduce hydraulic shock. The experiment's viability was verified through a literature review. During the hydraulic transmission trials, tests were conducted both with and without the inclusion of hydraulic accumulators in the hydraulic circuits. The purpose of this analysis is to determine the extent to which pressure increases in the absence of a damper at various costs, by manipulating the flow rate within the tube. In conclusion, this thesis confirms the efficacy of hydraulic accumulators in mitigating hydraulic shock by a comprehensive comparison and analysis of the gathered pressure response graphs. Hydraulic shock mitigation is more efficient at lower or higher flow rates. In the current hydraulic system, hydraulic shock is a frequently observed phenomenon. There are numerous theoretically possible solutions to address this issue. However, due to limitations in time and personal capabilities, it is necessary to have more comprehensive experimental equipment and facilities to validate these methods for mitigating hydraulic shock. Additionally, it is important to minimize the impact of external factors, such as environmental conditions, on the experimental results.