Development of a prototype hydraulic damping device for hot water heating circuit in pulse mode

Бюллетень науки и практики / Bulletin of Science and Practice

UDC 621.565.93/.95                                

The purpose of the course work is to describe the processes of hydraulics and heat transfer using differential equations[1-4].

To describe the processes, first an energy circuit is built, then equations are compiled, then the input and output through the black box are set, then the equations are calculated using the black box, equations for the image are written, then the complex resistance equation is compiled, the coefficients are distinguished, the frequency function for the energy circuit is written, the real and imaginary parts of the complex resistance are distinguished, with the help of which the amplitudefrequency and phase-frequency characteristics are calculated [5-8].

At the end, graphs are built based on the results of calculating the amplitude-frequency and phase-frequency characteristics, and conclusions are drawn from the graphs [9-12].

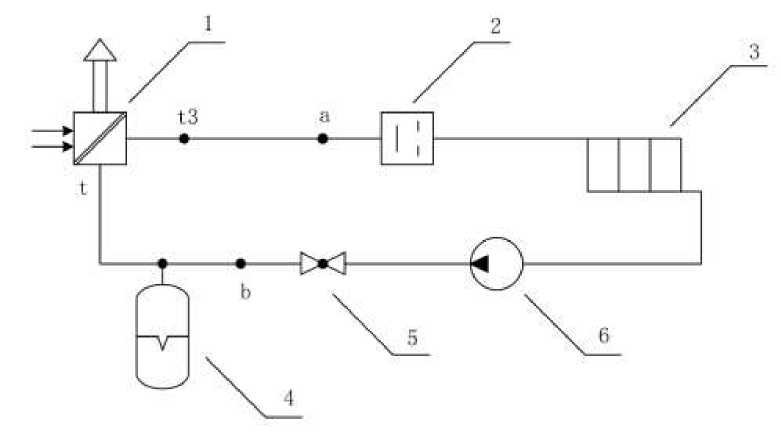
Figure 1. 1 - boiler; 2 – shock valve; 3 – heat exchanger; 4 – hydraulic accumulator; 5 –check valve; 6 – pump

Hot water or steam generated in the boiler 1 reaches the hydraulic accumulator 4 through the shock valve 2, heat exchanger 3, and water pump 6 and check valve 5. When the shock valve 2 is closed, the reverse wave of the water hammer will advance along the chain: hot water or steam first enters the hydraulic accumulator 4 and then reaches the check valve 5, water pump 6, heat exchanger 3 and pipe. At the same time, the pressure in the accumulator increases, and the kinetic energy is converted into an electric potential. The operation principle of the installed device is shown in Figure 1. The principle of heat transfer is shown in Figure 2.

In the course of the study, for a better understanding of the scheme, it was decided to study 2 characteristics of hydraulic and thermal, in order to better understand the nature of the forces arising and to more accurately determine the required parameters on the obtained model.

The hydraulic subsystem includes: 1 1 (which is compliance) taking into account the expansion of pipelines hear the valve; r 1 (active resistance) taking into account friction lesson in the pipe; m(water mass) in the pipeline and baseboard; r₂ (active resistance) taking into account friction lesson in the pipe; l₂ (compliance) taking into account the expansion of pipelines hear the valve.

In the first power circuit the hydraulic characteristics at the moment of closing of the shock valve is considered. This circuit contains 2 elements.

Figure 2. Hydraulic circuit

The circuit link equations:

(P = r1V12 + mV1 + r2Vl + P3

{ V = l 1 P + I 2 P 3 + V 2

Black box:

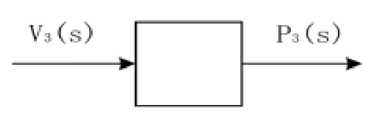
Figure 3. Black box for hydraulic energy circuit

Equations for P₃,V₂, V₂ ² :

Equations for P3,V2:

Equations for V 1 :

Equation for V 1 :

Equation for V 1² :

P 3 = P 30 + P 3

V 2 = V 20 + V 2

V 2² * V 220 + 2V 20 V 2

—

P 3 =P 3

—

V 2 = V 2

^V 1 = ^l 2 ^P 3 ^{+ V} 2 = ^l 2 ^P 3 ^{+ V} 20 ^{+ V} 2

V1 = I2P3 + V2

^V 2 = ^[l 2 ^P 3 ^{+ (V} 20 ^{+ V} 2 ^{)] 2} = ^V 220 ⁺ 2^l 2 ^V 20 ^P 3 ⁺ 2^V 20 ^V 2

Equation for P:

P = (Г1 + r2)(v220 + 2I2V20P3 + 2V20V2) + m(l2P3 + V2) + P30 + P3

= mV2 + 2V20(ri + r2)V2 + (Г1 + r2)V220 + ml2P3 + 2l2V20(ri + r2)P3 + P3 + P30

Equation for P :

P = mV₂ + 2У_2О(Г ! + r₂)V₂ + ml₂P₂ + 2/^0^ + r₂)P₃ + P 3 Equation for V:

V = l^mV + 2V20(ri + rJV + ml2P2 + 2^(4 + ^3 + P3]

+I2P3 + V20 + V2

= ml i V + 2l 1 V 2o (r i + ^ + V 2 + V 20 + ml i l 2 P 2 + 21 1^20^1 + ^3 + (l i + 1 2 )Р з = a i V 2 + CI2 V 2 + CI 3 V 2 + a₄V 20 + b iP'2 + Ь₂Р з + l^

Equation for images:

(a_is² + a₂s + a₃)V₃(s) = -(b_is³ + b₂s² + b₃s)P₃(s)

Complex resistance Z (s') :

a i s ² + a 2 s + а з Z⁽s) = —7—3—7—5—7— —b^³ — b₂s² — b₃s

Coefficients:

a_i = ml_i ^a 2 = ^2l i ^V 20 ^(r i ^{+ r} 2 ) ^a 3 = ¹ a₄ = 1 b_i = ml_il₂ ^b 2 = ^2l i ^l 2 ^V 20 ^(r i + ^r 2 ) b 3 = l i + l 2 Frequency function of the circuit: b 2

s ^ }&,j² = —1

Air

x

Water

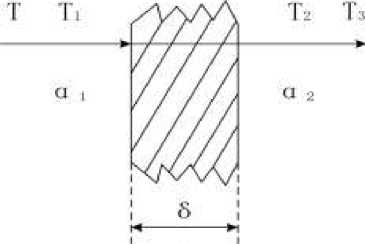
Figure 4. Part of the heat transfer plant: T - the temperature of hot water; T 1 ， T 2 - wall temperature; T 3 _-the temperature of the air; α_{1 -} convective heat transfer coefficient of water and left wall; α_{2 -} convective heat transfer coefficient of air and right wall; δ - the thickness of the wall surface; λ - Thermal conductivity of the wall

When the hot water flows through the wall, the convective heat transfer coefficient between the water and the left wall is h1, the temperature of the hot water is t, and the wall temperature rises to temperature t1. The heat is then transferred from the left wall to the right wall by heat conduction, where the wall thickness is δ, and the heat conduction coefficient is λ. When the temperature on the right wall rises to t2. The right wall is subjected to convective heat transfer with air, and the convective heat transfer coefficient is h2. Through convective heat transfer, heat is transferred to the air until the air temperature t3 reaches a stable state.

Figure 5. Heat transfer energy circuit

The circuit link equations:

Г t = Ы + Ы! + r₃q 2 + t₃

I q = C i t_x + C 2 t 2 + q 2

Black box:

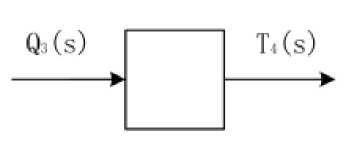
Figure 6. Black box for heat transfer

Equations for q_i :

^q 1 = ^C 2 ^t 2 ^{+ q} 2 = ^C 2 ^(r 3 ^q 2 ⁺ ^ з ) ^{+ q} 20 ^{+ q} 2 = ^C 2 ^r 3 ^q 2 ^{+ C} 2 ^t 3 ^{+ q} 20 ^{+ q} 2 Equations for t₂ :

^t 2 = ^r 3 q 2 ^+t 3

= ^r 3 ^q 20 ^{+ r} 3 ^q 2 ^{+ t} 30 ⁺ ^ 3

Equations for ti:

t i = r 2 q i + t 2

= ^r 2 (^C 2 ^r 3 ^q 2 ^{+ C} 2 ^t 3 ^{+ q} 20 ^{+ q} 2 ) ^{+ r} 3 ^q 20 ^{+ r} 3 ^q 2 ^{+ t} 30 ⁺ ^ 3

= C 2 r 2 r 3 ^q 2 + (r + r 3 )q 2 + (n + r 3 )q 20 + C 2 r 2 t 3 + t 3 + t 30 Equations for t 1 :

t i = C 2 r 2 r3q₂ + ⁽r 2 + r 3 )q 2 +C 2 r 2 t 3 + t 3

Equations for q :

q = C i t i + C₂t₂ + q 2

= ^C i ^[_^C 2 ^r 2 ^t 3 ^{+ t} 3 + ^C 2 ^r 2 ^r 3^q ₂ ^{+ (r} 2 ^{+ r} 3 ^)q 2 ^{] + C} 2 ^(r 3 ^q 2 ⁺ 4) + q 20 ^{+ q} 2

= C i C 2 r 2 r3q₂ + ⁽C i r 2 + C i r 3 + C 2 T 3~ )q 2 +q 2 + q 20 + C i C 2 r 2t3 + ⁽C i + C 2 )t 3 Equation for images:

(a i s² + 0 2 s + 0. 3 )7 3 (5) = -(b i s² + b 2 S + b3)Q 2 (s)

Complex resistance Z (s) :

—b_is² — b₂s — b₃ a_is² + a₂s + a₃

We derive the real part of the complex resistance:

—a i b i ^⁴ + (a₃b i — a₂b₂ + a^ti² — a₃b₃

Re(iQ) = --------------——---7—--------

(a3 — a^2)2 + a^2

We derive the imaginary part of the complex resistance:

Im(jQ') =

(a i b ^ —a ^ bi^+Ja ^ b ^ —a ^ b ^ )^ (a₃ — a₁Q.²)² + a^²

We obtain the amplitude-frequency function of the energy circuit:

A(j^) = ^Re(jQ)2 + Im(jO)2

Get the phase-frequency function of the energy circuit:

Im(j^) ^O^—arctg-Re^)

Construction of frequency characteristics of the circuit when changing at least three parameters (Table 1).

		CIRCUIT PARAMETERS				Table 1
m, kg	r^N/m • s	r2,N/m • s	l1,lit • s/kPa	l2,lit • s/kPa	P0,kPa	V0, lit/s	n0,kW
25.000	98.000	98.000	0.009	0.093	120.000	0.500	60.000
25.000	9800.000	9800.000	0.009	0.093	120.000	0.500	60.000
50.000	98.000	98.000	0.009	0.093	120.000	0.500	60.000

Dependency graphs are plotted based on the input values. For the best perception of graphs values are taken only those that affect the dependence. The values obtained for the first stage of the energy circuit are shown in Table 2.

Table 2 RECEIVED INFORMATION FOR HYDRAULIC

Ω	A i (jO)	ViW	A2m	V 2 (jW	A 3 (j®	V3W
1	16.902	1.525	10.811	1.570	13.639	1.521
2	5.425	1.543	5.405	1.571	5.923	1.544
3	3.859	1.553	3.604	1.571	7.005	1.557
4	3.516	1.559	2.703	1.571	19.464	1.563
5	3.752	1.562	2.162	1.571	15.267	1.566
6	4.666	1.564	1.802	1.571	5.278	1.568
7	7.307	1.566	1.545	1.571	3.192	1.569
8	23.803	1.567	1.352	1.571	2.302	1.569
9	15.585	1.568	1.201	1.571	1.811	1.570
10	5.640	1.569	1.081	1.571	1.500	1.570

Based on the results of the calculation, the graphs of the amplitude frequency response and phase-frequency response and frequency response of the circuit are constructed. Further in these graphs are under construction: For power circuits of the heat transfer calculations are conducted similarly and are written in Table 3.

In the process of modeling the hydraulic power circuit, it is found that with the increase of frequency, the frequency response of the hydraulic circuit first increases and then decreases, and finally becomes stable, and the amplitude gradually increases in this process. It can be found that after the parameter r is changed, the frequency response of the hydraulic circuit reaches a peak in advance, and then gradually decreases, while changing the water mass has little effect on this. The changes of parameters r and water mass have little effect on the amplitude, and both show a trend of gradual increase (Table 3, 4).

Table 3

RECEIVED INFORMATION FOR HEAT TRANSFER

n0, kW	r1, X/W	Ъ'С2 /W	Г 3 С2 /W	6, m	C 1 ,W /C2	C 2 ,W /°C2	A,W /(mC)	t o ,C
1.5	0.000385	0.0333	0.0333	0.002	0.0025	0.0025	150	70
1.5	0.0385	0.0333	0.0333	0.002	0.0025	0.0025	150	70
1.5	0.000385	0.0333	0.0333	0.002	0.25	0.25	150	70

Table 4

VALUE AMPLITUDE FREQUENCY RESPONSE FOR ENERGY CIRCUIT

Ω	Arm	ViW	A 2 (j^)	V2W	A3m	Фз№
1	0.067	0.000	0.105	0.000	0.067	0.004
2	0.067	0.000	0.105	0.000	0.067	0.008
3	0.067	0.000	0.105	0.000	0.067	0.013
4	0.067	0.000	0.105	0.001	0.067	0.017
5	0.067	0.000	0.105	0.001	0.067	0.021
6	0.067	0.000	0.105	0.001	0.067	0.025
7	0.067	0.000	0.105	0.001	0.067	0.030
8	0.067	0.000	0.105	0.001	0.067	0.034
9	0.067	0.000	0.105	0.001	0.067	0.038
10	0.067	0.000	0.105	0.002	0.067	0.042

The c1 and c2 parameters were most affected. When considering these graphs, a common feature can be distinguished, namely, the greater the difference between c1 and c2, the faster reaching the maximum frequency value. If the values of c1 and c2 are unchanged, then the system will be stable.

Conclusion

In the course of the work, the problems associated with this work and possible solutions are described. A constructive scheme of the experimental device is proposed and the principle of its operation is described in detail. The power circuit of the device is drawn up, each link is explained. Complex impedance, frequency function, amplitude-frequency characteristic and phase-frequency characteristic are obtained by mathematical transformation of the power circuit. The frequency response of the circuit is constructed.

Referances: