Диагностика двигателя внутреннего сгорания автомобиля по акустическому излучению двигателя

Современный автомобиль – это сложный технический аппарат, изготовленный из различных материалов с высокой точностью обработки деталей, но и снабженный современной электроникой. Первоначальные свойства, качество и параметры в процессе эксплуатации машин изменяются. Качество автомобиля обуславливается его динамичностью, топливной экономичностью, управляемость, проходимостью, приспосабливаемо-стью к техническому обслуживанию и ремонту. В настоящее время количество эксплуатируемых автомобилей в любой стране существенно превышает возможности их обслуживания и ремонта, в соответствии с рекомендациями производителей [1]. Выходом из сложившейся ситуации становится: во-первых, увеличение доли необслуживаемого оборудования, во-вторых, переход на ремонт машин и оборудования по фактическому состоянию. Но это возможно лишь при использовании методов и средств глубокой диагностики и долгосрочного прогноза состояния оборудования в процессе эксплуатации. Информация об изменении параметров двигателя непосредственно находится в акустическом сигнале, который генерирует двигатель в процессе работы[2,3].

Основная часть

Эффективность акустической диагностики не вызывает сомнения для любого механика. Хорошо известно из практики, что опытные механики, используя субъективное прослушивание машины, получают важную и достоверную информацию о её техническом состоянии, иногда даже с классификацией типа дефектов. Хорошо известны высказывания автогонщиков о том, что они чувствуют машину по рёву мотора. Однако существенную роль при этом играет наличие у одаренного механика опыта эксплуатации определённого типа машин, практически идеального слуха, хорошей памяти, интуиции и опыта системного анализа.

В массовом производстве, при обслуживании большого числа машин имеется явный дефицит механиков с изложенными выше качествами, поэтому стоит задача формализации процесса распознавания дефекта по акустическому сигналу, сравнимая по сложности с проблемой распознавания речи. Таким образом, акустическая диагностика представляет собой отрасль теории распознавания образов, а именно, образов, которые формируются на основе акустического сигнала. Для формирования этих образов могут подойти различные методы обработки сигналов. Но прежде чем рассматривать различные методы обработки сигналов надо выявить основные характеристики излучаемого двигателем акустического сигнала. Особенностью спектрального состава акустического излучения является наличие в спектре низкочастотных составляющих. Так, например, вращение коленчатого вала с круговой частотой 600 оборотов в минуту, соответствует 10 Гц, а частота взрыва смеси равна 40 Гц, соответственно вибрация корпуса двигателя будет составлять около 3 – 5 Гц, за счет возникновения стоячей вибрационной волны. Низкочастотные характеристики акустического сигнала несут основную информацию о работоспособности двигателя, поэтому существующие электронные приемники акустических сигналов для регистрации акустического излучения двигателя непригодны, так как они не принимают сигналы ниже 20 Гц.

Вторая особенность спектра акустического излучения двигателя заключается в том, что акустические сигналы от узлов и деталей находятся в узком спектральном диапазоне. Выделить некоторые спектральные составляющие, которые создает определенный узел или деталь не представляется возможным. Для того чтобы разделить сигналы, необходим параметр по которому можно произвести разделение сигналов. Таким параметром может служить амплитуда сигнала. Если рассматривать двигатель с данной позиции, то можно говорить, что одни узлы двигателя излучают акустические сигналы с большой амплитудой, другие со средней и малой амплитудой. Таким образом, если найти такой оператор, который сигналы с большой амплитудой переносил бы в область высоких частот, со средней амплитудой в область средних частот, а с малой амплитудой в область низких частот, то задача разделения сигналов была бы решена. Акустический сигнал двигателя представлял бы другой образ, но содержал в своем составе весь спектр генерируемых частот. Для решения такой задачи необходим нелинейный преобразователь.

Целью настоящей статьи является разработка приемника акустических сигналов в диапазоне 0,1Гц – 20 кГц, с нелинейным преобразованием входного сигнала и представлением выходного сигнала для автоматического распознавания образов.

Для решения поставленной задачи вначале разработаем математическую модель акустического излучения двигателя.

В самом общем смысле акустический сигнал, генерируемый ДВС, не является ни эргодическим, ни стационарным случайным процессом. Статистические характеристики акустического сигнала являются функцией двух переменных: элемента множества и текущего времени. В результате усреднения этих характеристик дважды - по множеству и по времени -можно получить статистические характеристики некоторого стационарного и эргодического процесса, названного «обобщенным» акустическим сигналом [4]

S (f )= SQL f2 +(f2 - f.)2 + f2 +(f2 + f1 )2

П где f - текущая частота; f1= 100,6 Гц; f2= 265,5 Гц; SQ =

T

- J ^{S2 (t} ) ^{dt   - эф-}

T ₀

фективное (среднеквадратическое) напряжение акустического сигнала.

Коэффициент корреляции обобщенного акустического сигнала будет иметь вид r Tt )=R(5) exP[- aT ]cos(^T)’

где a = 2 ^ 6 ; в = 2 n f ₂;   т = t — и.

Случайный процесс, заданный выражениями (1) и (2) может быть представлен в виде ряда некоррелированных случайных величин. При известном коэффициенте корреляции акустического сигнала такая задача сводится к решению линейного интегрального уравнения [5] T

J Pr ( t — и ) ф ( и ) ^Uu = ЛФ ( t );     — T <  t <  T,

— T

где Р - коэффициент, учитывающий среднеквадратическое значение акустического сигнала S(t); Ф(1), Л - соответственно собственные функции и собственные значения интегрального уравнения. С учетом результатов решения уравнения (3) акустический сигнал можно представить в виде

N

S ( t ) = li.m. \ Z ^{[ л} i C i ^С0Ф i t ⁺ V i ) ⁺ j ^Л i C 2 sin ( ^ it ⁺ V i ^)] .

N ^^ I i =1                                                                                    J

k - членная аппроксимация S(t) будет определяться выражением

k

^{S (} t ) = Е ^Л C ^{[ cos (Q} i t ⁺ V? ) + j ^{sin (Q} i t ⁺ V i ^)]

i =1

Обозначая Л₁.C_t = A , окончательно получим

k

S ⁽ t ) = Z ^{A [ cO}s ^(Q t + Ф и ) ⁺ j ^Sin ( ^Q t ⁺ V i )1

i =1

Выражение (6) описывает акустический сигнал с представлением в виде суммы частот. Спектр акустического сигнала представляет собой ли- нейчатый спектр, полностью соответствующий выражению (6).

Таким образом, разработанная математическая модель представления акустических сигналов может быть взята за основу при дальнейшем анализе и составлении модели для синтеза сигналов ДВС, которая представляет сумму ортогональных функций и может удовлетворять условиям эргодичности и стационарности.

Для преобразования акустического сигнала в удобный сигнал для преобразования в электрический сигнал может служить мембрана. Во-первых, она колеблется от низких частот и охватывает весь спектр акустических сигналов и во вторых технически реализуема.

С математической точки зрения мембрану можно рассматривать как мембрану с ограниченными размерами с центром тяжести и скоростью распространения акустических волн, определенной плотностью мембраны. В первом приближении в качестве ограничений примем условия: мембрана круглая и имеет центр тяжести в центре мембраны. При таком упрощении дифференциальное уравнение, с учетом начала координат в центре мембраны, описывающее отклонение точек мембраны U = U(r, φ , t) имеет вид [5]

д ² U    2 Г d ² U  1 d U   1 d ² U

----z— — a ----z--1----1--z--t" dt7      l d"2   r dr   r2 dp где r - радиус координата в полярной системе координат; p - угол в полярной системе координат; a — ^Т/р - натяжение мембраны; р - плотность мембраны.

Пусть на мембрану воздействует внешняя сила, подчиняющаяся синусоидальному закону Po sin tot, где Р0 -давление звуковой волны; to -круговая частота. В этом случае уравнение (7) представляется в виде неоднородного дифференциального уравнения в частных производных второго порядка д2 U  1 dU 1 д2U__^ d2U _  P0 sin rot dr2 + r дГ + r2 др2   a2 д2 "     T

с граничными условиями

U (0, p , t ) = 0,               U ( R , p , t ) = 0;                           (9)

и начальными условиями

U ( r , p ,0) = V ( r , p ,0),

∂ U

— = n ⁽ r , p ,⁰⁾, ∂ t

где R - радиус мембраны; V ( r , p ,0) - начальное смещение мембраны;

n (r , р ,0) - начальная скорость смещения мембраны.

Решение уравнения (8) будем искать в виде суммы

U ( r , р , t ) = U 1 ( r , р , t ) + U ₂( r , р , t ),                            (11)

где U^r, ф , t) - решение однородного уравнения (7); U₂(r, ф , t) - решение неоднородного уравнения (8).

Если время действия внешней силы значительно больше, чем время затухания основного тона t ₀ >>  т = 1 б , к моменту t o собственные колеба-

ния прекратятся и останутся только вынужденные.

Решение уравнения (8) будем искать в виде функции

U = P ( r , р ) sin ro t ,

где P ( r , р ) - функция, характеризующая амплитуду колебаний мембраны.

Подставляя (12) в (8), получим

д ² P  1 5 P   1 д ² P   го ² _n Р_о

--^- +--+ —т--Й---й" P + — д r ²    r д r   r ² др     a ²      T

Решение уравнения (13) будем искать в виде ряда Фурье по фундаментальным функциям колебаний мембраны

М 00

P ( r, ф) = ZZ Pmn ^- < r Ф(14)

m =0 n =0

P,( r .9) = ZZ Pomn V- (r ,9);(15)

m =0 n =0

cos — 9

^mn (r9) = Jm (k-nrX -     .(16)

sin — 9

R 2n где  Pmn = J J P(r. 9^mn (r. 9) rdrd9.

Проведем дифференцирование функций (15) и, подставив в выражение (13), получим решение дифференциального уравнения

U ( r . 9 . t )

М

E m 1 p

P_n J ^ (k r^s^cot __________ 0 mn m  mn   mn /       ___________

^ ^{2 J} m — ^ m n ^J m + 2 ⁺-- a ^{2 J} m ⁺-- mn a^J m + 1

rr

Из анализа выражения (17) следует, что частота колебаний мембраны в не граничных точках определяется вынужденной частотой колебаний.

При увеличении частоты to и при заданной амплитуде воздействующего сигнала существует линейная зависимость в поведении функции. При до- стижении граничной частоты

^ mn

= ^Ю < р

J m

2 ^ mn J,

—

2 m

r ^

a ² J -

—

^ mn

a m +1

r

.

возникает условие, при котором уравнение не имеет решения, и характер поведения функции становится неопределенным.

Таким образом, на поверхности мембраны возникает модальная структура. Моды между собой взаимно ортогональны и описываются ортогональными функциями (собственными функциями однородного дифференциального уравнения), амплитуда которых определяется амплитудой и частотой воздействующих сигналов и частотой собственных колебаний. Мембрана в данном случае работает как линейный элемент, преобразовывая акустические колебания в механические колебания мембраны.

При преобразовании механических колебаний в электрические целесообразно использовать метод голографической интерферометрии реального времени [6,7,8].

На рис. 1 приведена принципиальная схема измерения колебательного процесса центральной зоны мембраны. Здесь изображены: 1 – лазер. 2 -фокусирующая линза, 3 - регистрирующая среда (голограмма), 4 - мембрана, наклоненная под углом φ к голограмме, 5 – фотодетектор, 6 – компьютер.

Для возбуждения колебаний мембраны использовался акустическое излучение двигателя. Акустический сигнал воздействует на мембрану, которая начинает колебаться с учетом амплитуды входного сигнала. Лазерное излучение, попадая на мембрану, модулируется по фазе и попадает на фотодетектор. Второе излучение, которое попадает на фотодетектор, излучение дифракции с голограммы. Два этих излучения интерферируют и образуют интерференционную картину, преобразовывая фазовую модуляцию в амплитудную модуляцию светового излучения. Фотодетектор регистрирует амплитудные изменения и преобразует их в электрический сигнал, который поступает на аудио вход компьютера.

Рассмотрим применение метода голографической интерферометрии реального времени для измерения параметров колебаний центральной зоны мембраны, где в качестве информационной и опорной волны используется одна волна. На рис. 2, представлена эквивалентная оптическая схема измерения.

1                   2                        3  4         5

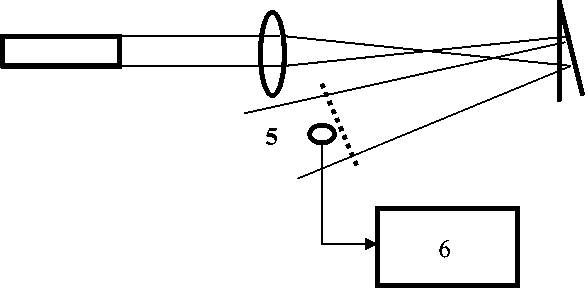
Рис.1. Оптическая схема однолучевого интерферометра реального времени. Здесь: 1 – лазер, 2 – фокусирующая линза, 3 – голограмма, 4 – мембрана, 5 –фотоприемник, 6 – компьютер.

На рисунке изображены: S 0 - точечный источник света, сфокусированный на поверхности исследуемого объекта , Г - голограмма, З -зеркало, S 1 - зеркальное изображение источника S 0 , R - расстояние от (.) S 0 до голограммы, L - расстояние от голограммы до зеркала по оптической оси,

α- угол наклона зеркала к голограмме.

На голограмме в исходном состоянии записывается изображение двух сферических волн a0

= a_c exp <  jk

R + —

2 R

;

a

= a_c exp <  jk

( R + L ) cos 2 a + L +

[ x - ( R + L ) sin2 a ] ² 2 [ ( R + L ) cos 2 a + L ]

где а с - амплитуда сферической волны на голограмме, приблизительно постоянная, при R>>x max и R>>L.

Предположим, что объект колеблется по гармоническому закону

Ar cos tot. При малом смещении [ — << 11 амплитуда сферической волны V R     / не изменится. В выбранной системе координат (.) S0 имеет координаты

( 0, - R ±A R + A r cos m t ) ,           а           (.)                      S i            -

[(R + AR + L -Ar cos mt )sin 2a, (R + AR + L - Ar cos mt )cos 2a + L ], где AR = R - R1I;-R1 - расстояние от точечного источника до голограммы на этапе измерения. Интенсивность интерференционного поля при смещении источника будет описываться выражением

I ( x ) = 2 a 2 + a 2 exp <  jk

- R - — + L + 2 R

[ x - ( R + L ) sin2 a ] ² 2 [ ( R + L ) cos 2 a + L ]

( R + L ) cos2 a-

I            2                    «7

- ^ + ^ac exp ^^- Jk

x ²

- R -   + ( R + L ) cos2 a + L +

2 R

[ x - ( R + L ) sin2 a ] ² - - 2 [ ( R + L ) cos 2 a + L ] •_-

При малых значениях угла α , будет справедливо неравенство

( R + L ) cos 2 a >>  ( R + L ) sin 2 a , тогда выражение (19) приводится к виду

J ( x ) = ² m ² J ( x ) - J  ( x )

m                     m —1           m — 2    ,

x или

= 2 ( m — 1 )

x

^Jm —1 ⁽ x )   ^Jm —2 ⁽ x )

^Jm ⁽ x )     ^Jm ⁽ x )

Из соотношений (23), (24) следует, если взять отношение амплитуд m-1 и m гармоник и вычесть отношение амплитуд m-2 и m гармоник, то полу- чим

A r = — / J n " ' ⁽ k^ tg [ k A R ( 1 + cos2 a ) ] — J " - 22 ⁽ k У) L                                (25)

2n 1 J" (kAr)   '    '          ,J   J" (kAr )J                                      V ’ n - четном;

— Il ^Jn —1 ^{( k A r} )

2 n [ J_n ( k A r )

Ctg

k A R ( 1 + cos 2 a ) —

^Jn —1 ( ^{k A r} ) ^Jn ^{( k A r} )

n - нечетном, при выполнении условия

^ ₌ —Arctg ⁽ 2 n — 2 ) 2 n ( 1 + cos 2 a ) ,

n - четном

^ ^ —ArcCtg ( 2 n — 2 ) 2 n ( 1 + cos 2 a )

n - нечетном.

Выражения (27) и (28) справедливы при условии Jn (kAr) ^ 0, что характеризует нелинейность преобразования, то есть в выражении (27) фазовый набег Л^ = kAr > п. При A^ < п выполняется условие нелинейного преобразования и

A r = - J , ( k A r ). п

Таким образом, известными параметрами являются: входное воздействие, функция преобразования светового излучения, спектр отклика на входное воздействие. Стоит задача - определить зависимость, отображающую функциональную деятельность оптико-голографического преобразования при воздействии входного сигнала.

Выходной сигнал можно представить в виде

S ( t ) = B ■ F [ A cos to t ],                                       (30)

где В - постоянный коэффициент, характеризующий линейный характер изменения функции преобразования светового излучения;

F - нелинейный оператор;

А - амплитуда входного воздействия, ω- частота входного воздей- ствия.

Предположим, что функция F(z) дифференцируемая и может быть разложена в степенной ряд с центральной точкой z=z0 , равной нулю. Тогда получим ряд Маклорена следующего вида [10]

F|(0)              F || (0)

F[A cos tot] = F(0) + —— A cos tot + —— A2 cos2 tot + — A3 cos3 tot 1!                      2!3!

F ^{| y} (0)    4     4             F ^{( n )} (0) n n

+-- A cos to t + ... +-- A cos to t + ...

4!

воспользовавшись соотношением [11]

cos a ■ cos в = ^ [cos(a - в)+ cos(a + в)], степенной ряд (32) можно представить в виде разложения в ряд по гармоническим составляющим го                               го го

s ( t ) = в ^ E a F ^{(2 i )} (°) + EE a F ^{(2 i + 2} n ) (°) cos 2 n to t +

I i =0

n =1 i =°

гого

+ EE a^F^{(2l +} 2n ^{- 1)}(°)sin ( 2 n - 1 ) to t } n =1 i =°

где

^a ° i

₌ ( 0,5 A ) 2 ^l , i ! i !

2 ( 0,5 A ) ^{2 1 + n} l ! ( i + n )

n - номер гармонической составляющей; i = 0,1, 2, ... и соответствует номеру коэффициентов при производных функции F*(0); n-ой гармонической составляющей, причем эти производные расположены так, что порядок производных возрастает.

Если предположить, что F(2i+n)(0) принимает поочередно значения 1

и -1, то выражение (31) сводится к виду

5 ( t ) = B ^ J_o ( A ) + 2 ^ J_2n ( A ) cos 2 n to t - 2 ^ J ₂„₊₁ ( A ) sin(2 n - 1 to t I .

n =1

Используя соотношения [7]

cos( z sin ф ) = J _o ( z ) + 2 ^ J₂ ((z )cos2 п ф ;

n =1

to

sin( z sin ф ) = 2 ^ J_{ln 4} ( z ) sin(2 n - 1) to t .

n =0

Вычтем из выражения (35) выражение (36)

cos(z sin ф) - sin(z sin ф) = Jo (z) + 2^ J2n (z)cos 2иф n =1

2 Z J 2 n -1 ⁽ z ^)sin(2 n ^- 1) ф

Сравнивая выражения (37) и (34) видим, что они полностью совпадают. Таким образом, передаточной функцией оптико-голографического преобразования является функция cos[A sin tot] - sin[A sin tot] = 0(t) .

При слабых сигналах входного воздействия частота колебаний выходного сигнала повторяет закон изменения акустического сигнала с увеличением амплитуды выходного сигнала. Превышение входного воздействия определенного порога осуществляется частотное кодирование амплитуды выходного сигнала, причем в этом случае будет подчиняться закону

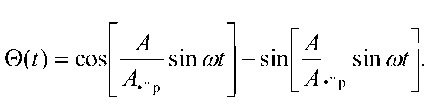
0 ( t ) = cos

A sin

A

A•”р sin tot

Полученные результаты свидетельствуют о том, что на этапе преобразования акустических сигналов оптико-голографический преобразователь выполняет роль нелинейного преобразователя интенсивности акустического сигнала в частоту и переносит сигналы с большой амплитудой в область высоких частот, со средней амплитудой в область средних частот, а с малой амплитудой усиливает сигнал и переносит в область низких частот.

Таким образом, теоретически и практически доказано, что реализация приемника акустических излучений двигателя по основным требованиям возможна и практически реализуема. Созданный приемник акустических сигналов на базе оптико-голографического преобразования акустических сигналов, регистрирует сигналы в диапазоне 0,1 Гц – 20 кГц и разносит сигналы по частотной оси по параметру амплитуды входного сигнала.

Экспериментальные исследования применения приемника акустических сигналов для диагностики ДВС проводилась на базе «Института безопасности дорожного движения». В качестве объекта исследования использовался бензиновый двигатель. Результаты экспериментальных исследований представлены в виде интегральных спектрограмм преобразованного акустического излучения двигателя, как исправного, так и с различными дефектами.

Бензиновый двигатель внутреннего сгорания в исправном состоянии генерирует акустические колебания, интегральный спектр которого представлен на рис. 3. (эталон). Интегрирование спектра проводилось в течение одной минуты. В дальнейшем интегральный спектр для всех акустических сигналов проводился в течении одной минуты.

Основные характеристики спектра исправного двигателя :

• 1.    Спектр охватывает диапазон частот от 86 Гц до 9 кГц.

• 2.    Более высокочастотные составляющие от 150 Гц до 9000 Гц убывают линейно.

Низкочастотный диапазон спектра можно условно разделить на 4 участка по амплитуде спектральных составляющих. Первый участок от 86 Гц до

190 Гц, второй участок от 190 Гц до 340 Гц, третий участок от 340 Гц до 690 Гц и четвертый участок от690 Гц до 1000 Гц. Спектр построен как бы ступеньками. Максимум амплитуды спектра приходится на диапазон частот от 1100 Гц до 1500 Гц. Этот диапазон частот можно назвать резонансным диапазоном для данного двигателя внутреннего сгорания.

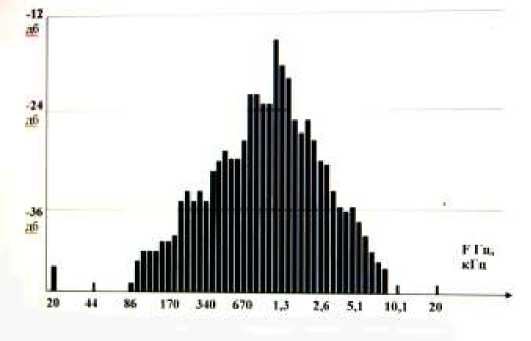
Рис. 3 Интегральный спектр акустического сигнала, генерируемого бензиновым двигателем внутреннего сгорания. Исходное состояние.

Изменения в спектре работающего двигателя будут характеризовать различные виды неисправностей в двигателе внутреннего сгорания. При выявлении отклонений от стандартного спектра акустического сигнала необходимо выявить причину возникновения неисправности, а так же какой элемент или узел приводит к искажению исходного спектра. Для решения данной проблемы можно идти двумя путями. Первый путь – это набор статистического материала, определение портрета неисправности и методом перебора выявлять характерную неисправность в двигателе. И второй путь – это набор ограниченного статистического материала и с уче- том характеристик излучения и нелинейного преобразования акустического сигнала диагностирующего прибора прогнозировать вероятность неисправности того или другого элемента или узла в двигателе внутреннего сгорания.

Второй путь требует дополнительных затрат на создание программного обеспечения, но является наиболее перспективным. Если представить интегральный спектр в виде элементарных геометрических фигур (рис. 3 а), то понятно, что программное обеспечение не потребует больших временных и материальных затрат [12]. Тем боле, что такие программы распознавания образов геометрических фигур уже имеются, осталось их модернизировать для данных целей. Такой путь развития диагностирующего оборудования позволяет использовать один прибор для диагностики практически всех двигателей внутреннего сгорания, независимо от их конструктивных решений.

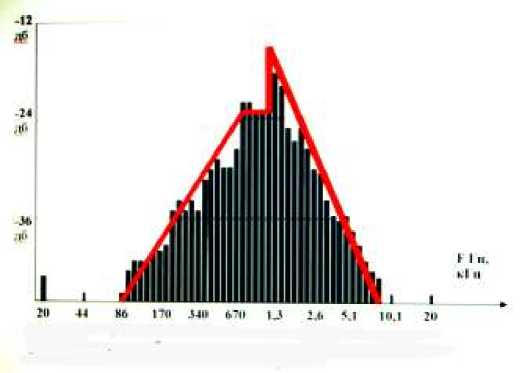
Рис. 3а. Интегральный спектр акустического сигнала, генерируемого бензиновым двигателем внутреннего сгорания. Представление спектра в виде геометрических фигур для машинного распознавания образов.

Представление интегрального спектра в виде элементарных геометрических фигур упрощает процесс распознавания и ускорят диагностирование ДВС.

Проведем анализ характерных неисправностей в двигателе внутрен- него сгорания. На рис 4 представлен интегральный спектр двигателя, в котором не работает 2-й цилиндр.

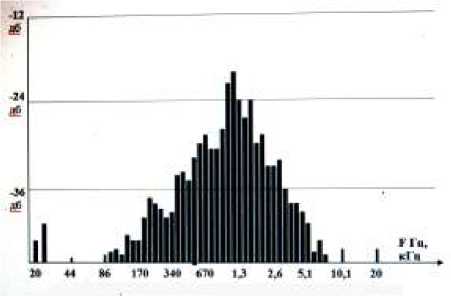
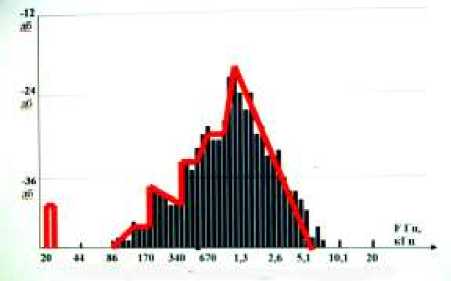
Рис. 4. Не работает 2-й цилиндр в двигателе внутреннего сгорания.

Характерной особенностью данного спектра является наличие дополнительного сигнала в области низких частот (20 Гц), что приводит к усилению колебательного процесса всей конструкции двигателя. Появление провалов в ступеньках на низких частотах и деление низкочастотной ступеньки на две. Кроме этого стоит отметить уменьшение амплитуды спектральных составляющих и смещение резонансной частоты в область 900 – 1200 Гц, а так же образование пяти ступенек в области верхних частот. Эти особенности характерны для случая, когда выйдет из строя не только 2-й цилиндр, а предположим 1-й, или 3-й, или 4-й цилиндр.

А теперь рассмотрим характер изменения спектра акустического сигнала, когда не работают два цилиндра. На рис. 5 представлен спектр сигнала, генерируемый двигателем, у которого две форсунки отключены, и горючая смесь не попадает в 3 и 4 цилиндры.

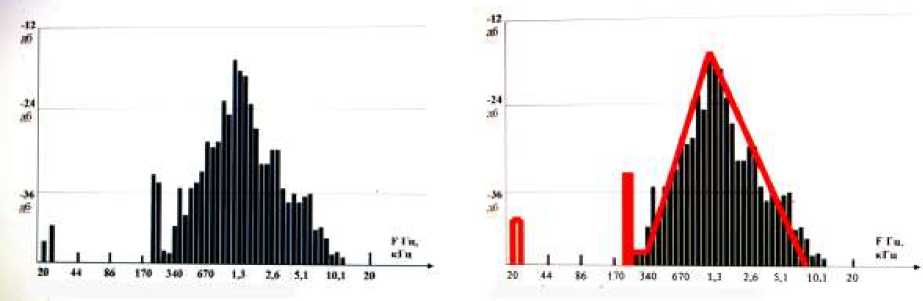
Рис. 5 . Две форсунки отключены, и горючая смесь не попадает в 3 и 4 цилиндры.

Как и в предыдущем случае, когда не работал один цилиндр, в области нижних частот образуется дополнительный сигнал, который характеризует дополнительную вибрацию всего двигателя. На низких частотах 230Гц, 260 Гц резко возрастают амплитуды спектральных составляющих. В то же время спектральные составляющие от 86 Гц до 290 Гц отсутствуют, зато в области верхних частот спектр расширяется до 10,1 кГц. Максимальные спектральные составляющие располагаются в диапазоне 1 – 1,6 кГц, то есть резонансная частота двигателя частично сместилась в область верхних частот. Что произойдет со спектром, если отключить 1 и 2 форсунки. Существенных изменений в спектре не произойдет. Амплитуды спектральных составляющих на частотах 230 и 260 Гц уменьшатся, а амплитуды частотах 290, 310 и 340 Гц вырастут, создав еще одну ступеньку.

Рассмотрим случай, когда не работают также 2 цилиндра 1 и 4, но в этом случае бензиновая смесь поступает в цилиндры, а вот поджога горючей смеси не происходит. На рис. 6 представлен интегральный спектр работающего двигателя с двумя цилиндрами.

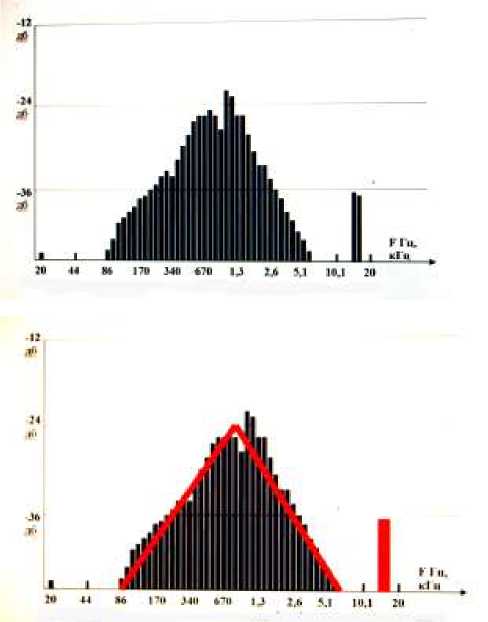
Рис. 6. Не работает катушка зажигания, 1 и 4 цилиндры отключены.

В этом случае мощность двигателя резко падает, вибрация двигателя уменьшается, что характеризует амплитуда спектральной составляющей на 20 Гц. Спектр акустического сигнала, становится похож на треугольник. В верхней области частот в районе 15 кГц появляются две спектральные составляющие, которые характеризуют сгорание топливной смеси за пределами цилиндра, что усиливает вибрацию двигателя, выравнивая ее по спектральным составляющим как в области нижних частот, так и верхних частот и одновременно уменьшает спектр в верхних частотах до 5,1 кГц.

Датчик давления воздуха не выдает в электронный блок управления корректный сигнал, на оборотах холостого хода электронный блок управления выдает команду по программе управления максимально близкой по характеристикам к эталонному образцу, спектр сместился в сторону высоких частот от 150 до 11000 Гц, на частоте 170-1300 Гц уменьшение амплитуды по сравнении с эталонным образцом, амплитуда резонансных частот снизилась, а диапазон увеличился от 1300 до 2000 Гц (рис.7).

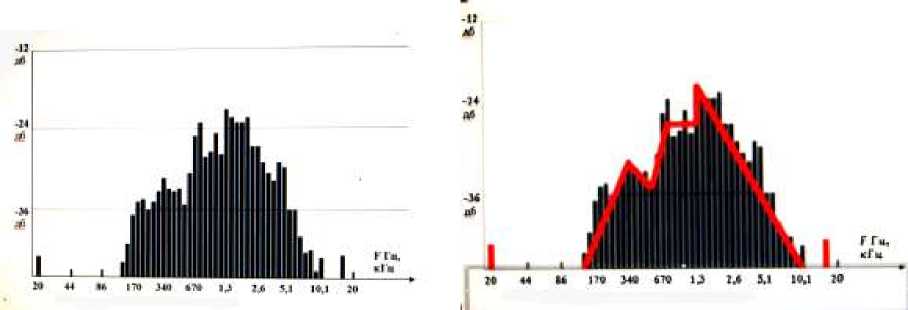
Рис. 7. Отключен датчик давления воздуха, частота вращения коленчатого вала 800 оборотов в минуту

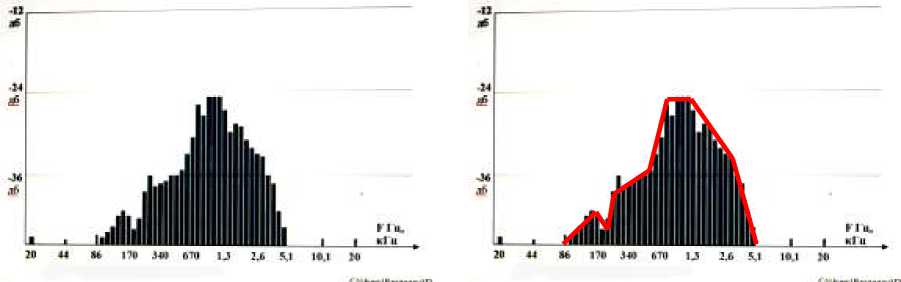
Рис. 8. Отключен датчик давления воздуха, частота вращения коленчатого вала 2000 оборотов в минуту

Электронный блок управления выдает команду на работу двигателя в защищенном режиме, но с учетом возросшей частоты коленчатого вала до 2000 оборотов в минуту, диапазон спектра уменьшился в области высоких частот, а на низких частотах наблюдаем провал амплитуды, резонансные частоты сместились в область низких частот (рис. 8).

Заключение

Проведенный анализ структуры интегрального спектра позволяет сделать вывод о целесообразности использования акустического метода диагностики работоспособности двигателей внутреннего сгорания. Полученные результаты показывают об однозначности структуры спектра и дефекта двигателя.

Таким образом, наиболее доступный физический параметр ДВС, а именно акустическое излучение двигателя, при определенных условиях обработки и создании портрета интегрального спектра акустических сигналов позволяет с высокой достоверностью осуществлять идентификацию рабочего состояния двигателя с указанием дефектов.

Полученные результаты позволяют утверждать о целесообразности введения в паспортные данные автомобиля интегрального акустического спектра (портрета) исходного состояния автомобиля. В дальнейшем этот портрет может лечь в основу диагностики двигателя, что существенно упростит процесс диагностики и сократит время ремонта автомобиля.