Диагностика КВ-радиоканала по данным возвратно-наклонного зондирования ионосферы непрерывным ЛЧМ-сигналом

Возвратно-наклонное зондирование (ВНЗ) прочно вошло в практику исследования ионосферы наряду с вертикальным (ВЗ) и наклонным (НЗ) зондированием начиная с 40-х гг. XX в., и имеется опыт по применению его для прогнозирования условий работы на линиях радиосвязи [Benner, 1949; Кабанов, Осетров, 1965; Чернов, 1971]. При ВНЗ сигнал подвергается влиянию тех же факторов, которые действуют на сигналы магистральных радиолиний. Поэтому естественно ожидать, что по параметрам сигнала ВНЗ и их изменениям можно предсказать условия распространения на линиях связи. Кроме того, сигнал ВНЗ несет в себе информацию о состоянии ионосферы на удалении несколько тысяч километров от места наблюдения в любом заданном направлении. Это существенно дополняет возможности, предоставляемые ионосферными станциями ВЗ в изучении ионосферы и прогнозирова- нии ее параметров. Существует несколько основных подходов к определению характеристик радиосвязи по данным ВНЗ. Наиболее широко распространенный подход связан с решением так называемых обратных задач, когда из данных ВНЗ ионосферы определяются ее количественные параметры. Как правило, в качестве измеряемых характеристик используются задержки зондирующего сигнала, соответствующие переднему фронту сигнала ВНЗ [Benito et al., 2008; Fridman et al., 2012; Norman et al., 2013; Zhu et al., 2015; Feng et al., 2016]. Использование таких методов обычно требует больших временных затрат на ЭВМ, что значительно снижает возможности использования средств ВНЗ для контроля условий работы на коротковолновых трассах.

Одним из возможных путей оперативного прогнозирования характеристик радиосвязи является метод прямой диагностики радиоканала, позволяющий по зондирующему сигналу определять характеристики радиоканала, минуя коррекцию параметров ионосферы [Куркин и др., 1993] . Данный подход применяется в случаях, когда диагностическая трасса НЗ совпадает с интересующей радиотрассой или лежит в секторе возвратно-наклонного зондирования. В настоящей работе излагается метод оперативной диагностики КВ-радиоканала по результатам автоматической обработки и интерпретации ионограмм возвратно-наклонного зондирования, полученных с помощью ЛЧМ-ионозонда, разработанного в ИСЗФ СО РАН [Brynko et al., 1988; Подлесный и др., 2013] . Результаты интерпретации сигналов ВНЗ и построения треков являются исходными данными для определения максимальных применимых частот (МПЧ) и дистанционно-частотных характеристик (ДЧХ) наклонного зондирования ионосферы на заданные дальности. В дальнейшем результаты оперативной диагностики КВ-радиоканала по текущим данным ВНЗ используются для восстановления параметров ионосферы в секторе зондирования.

МЕТОД ПРЯМОЙ

ДИАГНОСТИКИ РАДИОКАНАЛА

При моделировании характеристик сигналов наклонного и возвратно-наклонного зондирования и анализе экспериментальных данных были выявлены следующие слабо меняющиеся при вариациях параметров ионосферы соотношения [Куркин и др., 1993; Ponomarchuk et al., 2009, 2012] :

• •    отношение группового пути P m , соответствующего переднему фронту сигнала ВНЗ, к дальности до границы освещенной зоны D m ( P m / D m );

• •    ДЧХ мода наклонного распространения на относительной сетке частот β= f / f _m, где f _m — МПЧ мода для рассматриваемой дальности ( P (β));

• •    ДЧХ сигнала ВНЗ по переднему фронту на относительной сетке частот ν= f / f _m, где f _m — МПЧ для максимальной дальности распространения сигнала ВНЗ.

Данные соотношения позволяют решать следующие задачи оперативной диагностики декаметро-вого радиоканала:

• •    интерпретация модов распространения на экспериментальных ионограммах ВНЗ по точкам со значимой амплитудой, полученным в результате вторичной обработки;

• •    восстановление ионограмм ВНЗ по фрагментам треков, когда технические возможности ионозонда или условия на трассе распространения не позволяют получить частотные зависимости группового пути какого-либо мода;

• •    оперативное определение МПЧ и ДЧХ сигналов НЗ на заданной радиотрассе по данным ВНЗ.

Положение границы освещенной зоны находится с помощью ДЧХ сигналов ВНЗ по переднему фронту, поскольку максимум в амплитудном рельефе сигнала ВНЗ близок по групповому пути к границе переднего фронта [Dyson, 1991; Ponomarchuk et al., 2009] . Поэтому интерпретацию ионограмм ВНЗ можно проводить на основе расчета частотной зависимости минимального группового пути P _m( f ), соответствующего точке смыкания верхнего и нижнего лучей для сигналов НЗ [Ponomarchuk et al., 2016] . Рабочая частота f для соответствующей дальности D m ( f ) является максимальной применимой частотой радиосвязи. Моделирование характеристик сигналов ВНЗ и НЗ проводится в рамках волноводного подхода c использованием модели IRI [Ilyin et al., 1996; Bilitza, Reinisch, 2008; Ponomarchuk et al., 2009; Пономарчук и др., 2014] .

ОБРАБОТКА

И ИНТЕРПРЕТАЦИЯ ДАННЫХ

При оперативном прогнозировании характеристик радиосвязи определяющим фактором является автоматизация процесса вторичной обработки и анализа поступающей диагностической информации о состоянии КВ-радиоканала. Обработка ионограмм включает следующие этапы [Grozov et al., 2012; Ponomarchuk et al., 2012; Грозов и др., 2013] :

• а)    предобработка ионограмм для удаления шума с изображения и улучшения амплитудных характеристик;

• б)    сжатие данных, позволяющее провести значительное сокращение их объема без существенной потери полезной информации.

Предобработка ионограмм заключается в ее очистке от шумовых составляющих с целью выделения полезного сигнала, а также в удалении одиночных выбросов, по интенсивности сравнимых с полезным сигналом. Для исключения шума применяются локальные методы сглаживания, имеющие высокую вычислительную эффективность и возможность обработки изображений в реальном масштабе времени. Для удаления шума на изображении и восстановления отсчетов сигнала используется медианный фильтр, который позволяет сглаживать помехи и уменьшать размытие границ треков, а также восстанавливать значения в разрывах треков. При переходе между реализациями на соседних частотах низкая корреляция между шумовыми помехами приводит к тому, что помеха становится импульсной и лучше всего удаляется медианным фильтром.

Методика сжатия данных применяется для выделения точек со значимой амплитудой, физически соответствующих величинам — моментам прихода сигнала по переднему фронту сигнала или максимуму амплитудного рельефа. Для отсева одиночных артефактов, частичного восстановления данных и выявления первичного трека на ионограмме эффективен механизм клеточного автомата. Клеточные автоматы — это дискретные динамические системы, поведение которых полностью определяется локальными взаимными связями элементов этих систем. В результате такой обработки остаются точки на гребнях треков и незначительная часть шума. Реализованный алгоритм позволил достигнуть сжатия исходной информации в 5–10 раз в зависимости от уровня шума и диффузности.

На рис. 1 приведены ионограмма ВНЗ ( а ) и результаты вторичной обработки данных ( б ). Пункт излучения — Усолье-Сибирское (52.88° N, 103.26° E). Пункт приема — Торы (51.8° N, 103.0° E). Азимут излучения — 55°. Время регистрации — 08:40 UT 25.09.2005. Используемый ЛЧМ-ионозонд относится к маломощным системам с мощностью передатчика менее 1 кВт, поэтому в режиме ВНЗ он позволяет регистрировать рассеянные сигналы в пределах максимальной дальности одного скачка (~3000÷4000 км). На ионограмме на рис. 1 выделенные рассеянные сиг-

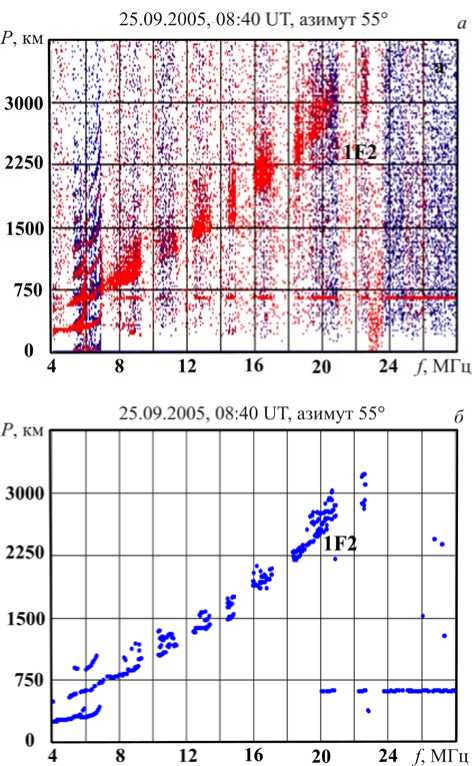
Рис. 1. Ионограмма ВНЗ ( а ) и результаты вторичной обработки ( б ) (25.09.2005, 08:40 UT)

The diagnostics of HF radio channel… налы ВНЗ соответствуют однократному отражению от слоя F2.

Алгоритм восстановления ДЧХ ВНЗ базируется на адиабатической зависимости минимального группового пути рассеянного земной поверхностью сигнала на относительной сетке частот ν= f / f _m при изменении параметров ионосферы. Для прогнозных параметров ионосферы на сетке частот проводится расчет ДЧХ сигналов ВНЗ по переднему фронту. Моделирование характеристик сигналов ВНЗ по переднему фронту проводится в рамках волноводного подхода с использованием модели IRI [Bilitza, Reinisch, 2008; Ponomarchuk et al., 2009] . Прогнозная ДЧХ сигнала ВНЗ пересчитывается на относительную сетку частот ν. В качестве частоты f _m выбирается МПЧ для максимальной дальности распространения сигнала. После вторичной обработки экспериментальной ионограммы ВНЗ имеется матрица экспериментальных точек, соответствующая двумерному массиву значений группового пути P_i на сетке частот f j для точек со значимой амплитудой. Экспериментальные точки также переводятся на относительную сетку частот ν. Алгоритм идентификации мода распространения на ионограмме ВНЗ в автоматическом режиме заключается в определении максимума гистограммы распределения числа экспериментальных точек, попадающих в модельную маску, построенную по долгосрочному прогнозу, при изменении частоты f _m на относительной сетке частот ν= f / f m .

На рис. 2 приведены результаты вторичной обработки и интерпретации ионограммы ВНЗ. Линиями 1 и 2 показаны результаты моделирования P _m и D _m по долгосрочному прогнозу, линией 3 — интерпретированная ДЧХ ВНЗ, черными точками — точки со значимой амплитудой сигнала ВНЗ.

ОПЕРАТИВНАЯ ДИАГНОСТИКА

Разработанные методы автоматической обработки и интерпретации ионограмм ВНЗ позволяют решать следующие задачи оперативной диагностики декаметрового радиоканала по текущим данным регистрации ионограмм ВНЗ:

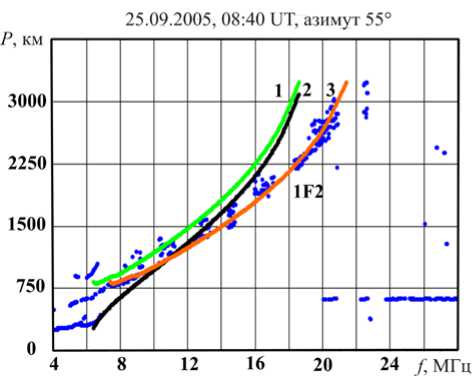
Рис. 2. Результаты вторичной обработки и интерпретации ионограммы ВНЗ, полученной 25.09.2005 в 08:40 UT: линия 1 — P _m, линия 2 — D _m, линия 3 — ДЧХ ВНЗ, черные точки — точки со значимой амплитудой сигнала ВНЗ

• •    оперативное определение МПЧ и ДЧХ сигналов НЗ для мода распространения 1F2 на заданной радиотрассе по данным ВНЗ;

• •    восстановление пространственного распределения электронной концентрации в секторе зондирования ионосферы ЛЧМ-ионозондом в режиме ВНЗ.

Расчет МПЧ сигнала НЗ при заданной длине радиотрассы по текущей ДЧХ сигналов ВНЗ базируется на адиабатическом соотношении P m / D m . На первом этапе для прогнозных параметров ионосферы рассчитываются дистанционно-частотные характеристики P _m( f ) и D _m( f ). Для заданной дальности D ₀ вычисляется отношение η= P m / D 0 . Далее на реальной ДЧХ ВНЗ по переднему фронту сигнала определяется частота, для которой групповой путь равен значению P =η D ₀. Рассчитанная таким образом частота будет являться реальной частотой f m для дальности D ₀. После определения МПЧ для заданной дальности по текущим данным ВНЗ можно рассчитать реальную ДЧХ НЗ соответствующего мода распространения. ДЧХ наклонного зондирования для дальности D 0 рассчитывается по долгосрочному прогнозу параметров ионосферы на относительной сетке частот β= f / f _m ^прогн . Реальная ДЧХ НЗ на текущий момент времени восстанавливается из прогнозной умножением β на f m [Куркин и др., 1993; Grozov et al., 2012] .

На рис. 3 приведены результаты пересчета прогнозных ДЧХ НЗ мода 1F2 в реальные задержки сигнала на сетке дальностей по МПЧ, восстановленным по текущей ДЧХ сигнала ВНЗ, приведенной на рис. 2. Время регистрации — 08:40 UT 25.09.2005. Геометрия сектора зондирования в данном эксперименте приведена на рис. 4. Центральный азимут сектора 55° совпадает с направлением на Магадан.

Для иллюстрации возможностей метода коррекции МПЧ по данным ВНЗ на рис. 5 приведены результаты сопоставления ДЧХ НЗ для односкачкового мода 1F2 на удалении 3000 км от пункта излучения с экспериментальной ионограммой НЗ, полученной на трассе Магадан—Торы (длина трассы ~3000 км) в 08:45 UT. Штриховой линией показаны результаты моделирования ДЧХ НЗ в рамках волноводного подхода с использованием модели IRI, сплошной — результаты восстановления.

На рис. 6 приведены временные вариации МПЧ односкачкового мода 1F2 для дальности 3000 км в направлении Магадана для 18 и 19 ноября 2005 г. Для корректировки МПЧ на заданную дальность использовались данные, полученные по результатам автоматической обработки и интерпретации ионограмм ВНЗ [Ponomarchuk et al., 2016] . Сплошной линией обозначены МПЧ, рассчитанные по результатам восстановления ДЧХ НЗ по текущим данным ВНЗ. Здесь же штриховой линией показаны экспериментальные значения максимальных наблюдаемых частот (МНЧ) на трассе наклонного зондирования Магадан—Торы в этот период наблюдений. Вариации МНЧ около 2 МГц с периодами 1– 2 ч обусловлены перемещающимися ионосферными

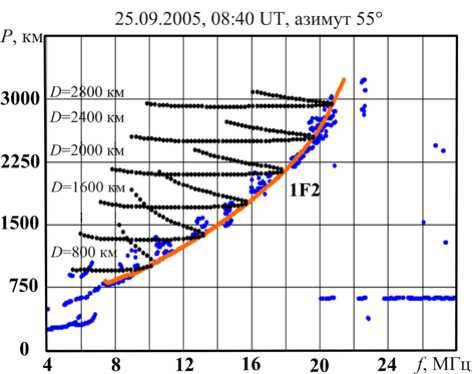
Рис. 3. Результаты вторичной обработки, интерпретации ионограммы ВНЗ (25.09.2005, 08:40 UT) и ДЧХ НЗ на сетке дальностей

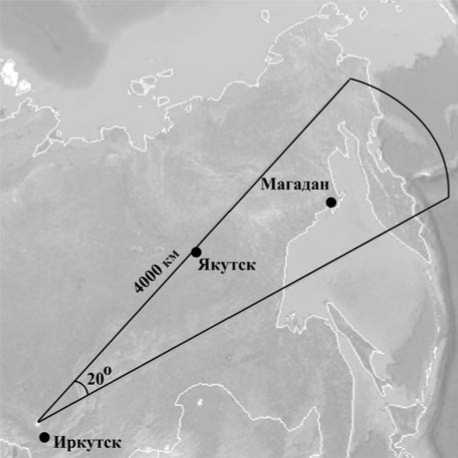
Рис. 4. Сектор зондирования с центральным азимутом 55°

Магадан-Торы

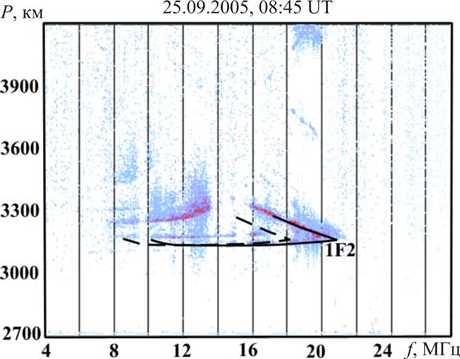
Рис. 5. Ионограмма НЗ (25.09.2005, 08:45 UT) и полученная ДЧХ НЗ для 08:40 UT того же дня: штриховая линия — по модели IRI; сплошная линия — в результате восстановления

18.11.2005

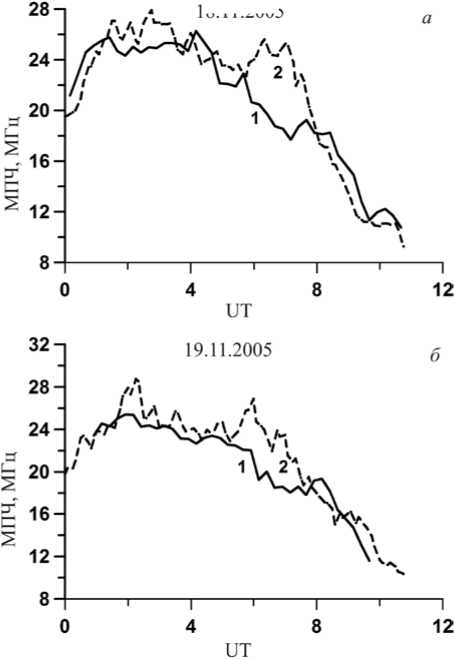
Рис. 6. Временные вариации реальных и восстановленных МПЧ на трассе Магадан—Торы: линия 1 — восстановленная МПЧ, 2 — реальная МНЧ

но-гиперболической аппроксимации монотонного высотного профиля электронной концентрации. В работе [Krasheninnikov, Liannoy, 1990] авторами для повышения точности восстановления профиля электронной концентрации была использована кусочно-квазипараболическая аппроксимация квадрата плазменной частоты. Для оперативного расчета параметров ионосферы в работе [Котович и др., 2006] предложена методика обращения ДЧХ наклонного зондирования в высотно-частотную характеристику (ВЧХ) вертикального зондирования вблизи средней точки трассы с использованием модифицированного метода Смита (метод кривых передачи). В рамках данной методики реализован алгоритм расчета ВЧХ в средних точках радиотрасс, расположенных в секторе ВНЗ, с последующим восстановлением профиля электронной концентрации [Михайлов, 2000] .

В модифицированном методе кривых передачи линейная связь между частотами вертикального f о и наклонного зондирования f H определяется выражением f _Н =kf _оsecφ, где φ — угол падения луча на слой, k — коэффициент Смита, учитывающий сферичность Земли. Угол падения φ луча на слой, согласно теореме эквивалентности, в модифицированном методе кривых передачи связан с действующей высотой h' следующей формулой:

ф = arctg

sin ( D / 2 R ) x - cos ( D / 2 R )

возмущениями (ПИВ) на трассе [Ivanova et al., 2011] . Рассчитанные по текущим данным ВНЗ МПЧ согласуются с экспериментальными МНЧ (рис. 6). Для коррекции МПЧ с учетом перемещающихся ионосферных возмущений в качестве входных данных необходимо выбирать на ионограмме ВНЗ семейство точек со значимой амплитудой, соответствующих моментам прихода рассеянных сигналов с различных направлений. Такая задача решается с использованием данных когерентных радаров SuperDARN. Характеристики принимаемого радаром SuperDARN сигнала ВНЗ используются для диагностики ПИВ среднего и крупного масштабов [Oinats et al., 2016] .

Таким образом, развитые методы прямой диагностики радиоканала по данным ВНЗ позволяют оперативно корректировать МПЧ и ДЧХ сигналов НЗ на заданной радиотрассе по текущим данным ВНЗ в секторе зондирования без восстановления параметров ионосферы.

Результаты оперативной диагностики радиоканала по данным ВНЗ — ДЧХ сигнала ВНЗ по переднему фронту Pm(f), восстановленные ДЧХ НЗ и МПЧ для заданной радиотрассы — могут быть использованы также в качестве входных параметров при решении обратной задачи определения параметров ионосферы по данным зондирования. Обратная задача определения параметров ионосферы по ДЧХ НЗ рассматривалась многими авторами. В работе [Smith, 1970] предложено ее решение путем сведения системы интегральных уравнений к системе нелинейных уравнений посредством кусоч- где

R + h'

x = R ’

R — радиус Земли. Групповой путь распространения декаметрового сигнала P при наклонном распространении определяется следующим образом:

P = 2 R

sin ( Q-ф ) sin ф

где Ω — arcsin( x sinφ). Ионограмма НЗ представляет собой зависимость группового времени распространения волны от частоты зондирования. Для каждой частоты f _H групповое время распространения сигнала зависит от высоты отражения. Для нахождения искомого значения h' , соответствующего задержке сигнала на частоте f _H на ионограмме НЗ при одно-скачковом распространении (мод 1F2), выполняется, начиная со значения 200 км, перебор с шагом 200 м действующих высот, по которым рассчитывается групповое время распространения. В результате находится значение группового пути, равное экспериментальному значению на выбранной частоте. Согласно закону секанса, по частоте f H наклонного зондирования рассчитывается значение частоты f о вертикального зондирования. Таким образом, проводится расчет ВЧХ ВЗ в средней точке трассы. Для реконструкции высотного профиля плазменной частоты f e ( h ) развит метод численного решения интегральных уравнений посредством модифицированного метода Джексона с повышением точности в областях максимумов слоев (прикритических частот) и долин [Михайлов, 2000] . По полученному f _e( h )-про-

Частота, МГц

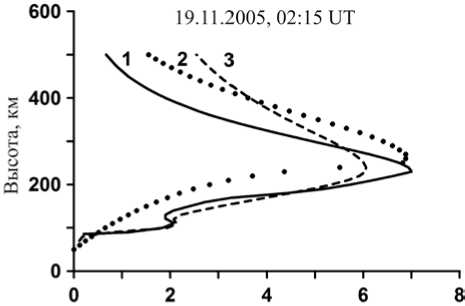
Рис. 7 . Профили плазменной частоты f _e( h ): 1 — реальный, 2 — восстановленный, 3 — по модели IRI

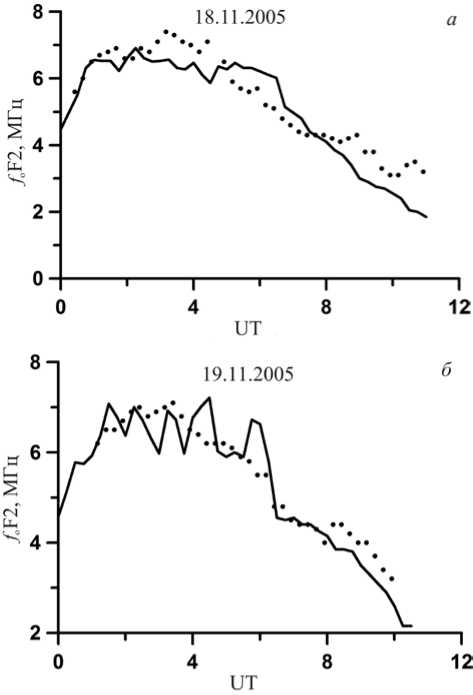
Рис. 8. Временные вариации критической частоты слоя F2 в средней точке трассы Магадан—Торы: сплошная линия — экспериментальные значения foF2 на ст. «Якутск», точки — восстановленные значения foF2 в средней точке трассы филю определяются ионосферные параметры слоя F2: критическая частота foF2 и высота максимума hmF2. Точностные характеристики метода расчета параметров ионосферы вблизи средней точки трассы по текущим данным НЗ приведены в работе [Ponom-archuk et al., 2015].

На рис. 7 в качестве примера приведены профили плазменной частоты fe(h), полученные на удалении 1500 км от пункта излучения в направлении зондирования 55°. Сплошной линией показан профиль fe(h), полученный по данным вертикального зонди- рования в Якутске (62° N, 129.7° E) для 02:15 UT 19.11.2005, штриховой линией — профиль fe(h), рассчитанный по модели IRI [Bilitza, Reinisch, 2008], точками — результаты расчета fe(h) по ВЧХ ВЗ, восстановленной из ДЧХ НЗ для дальности 3000 км. ДЧХ НЗ была рассчитана по текущим данным ВНЗ в этот период времени. Разница по широте станции ВЗ и средней точки трассы (58.2° N, 124.2° E) составляет почти 4°, и расстояние между точками примерно равно 500 км, поэтому данные ст. «Якутск» лишь частично могут быть контрольными при верификации методики диагностики параметров ионосферы.

Для иллюстрации метода диагностики параметров ионосферы по данным ВНЗ на рис. 8 приведены результаты определения критической частоты слоя F2 в средней точке радиотрассы Магадан—Торы по ДЧХ НЗ, восстановленной по текущим данным ВНЗ, полученными 18 и 19 ноября 2005 г. (см. рис. 6). Сплошной линией на рис. 8 показаны вариации критической частоты по данным станции ВЗ, расположенной в Якутске. Вариации f o F2 около 1 МГц и c периодами около 1 ч обусловлены наличием перемещающихся ионосферных возмущений над Якутском в эти дни [Куркин и др., 2014] . Значения критической частоты слоя F2, рассчитанные по ДЧХ НЗ, восстановленной из данных ВНЗ, согласуются с экспериментальными данными.

Отметим, что аналитические выражения для P m и D _m, полученные в сферически-симметричном волноводе с модельным квазипараболическим профилем электронной концентрации, позволяют определять критическую частоту и высоту максимума слоя F2 по текущим данным ВНЗ по переднему фронту сигнала [Li et al., 2013] .

ЗАКЛЮЧЕНИЕ

В работе излагается метод оперативной диагностики КВ-радиоканала по результатам автоматической обработки и интерпретации ионограмм возвратно-наклонного зондирования ионосферы, полученных с помощью ЛЧМ-ионозонда. Используются слабо меняющиеся в различных гелиогеофизи-ческих условиях соотношения частотных зависимостей групповых характеристик сигналов НЗ и ВНЗ. Интерпретация сигналов на ионограмме проводится по результатам расчета дистанционно-частотной характеристики ВНЗ по переднему фронту сигнала. Моделирование характеристик распространения радиоволн проводится в рамках волноводного подхода с использованием модели IRI. Результаты идентификации регистрируемых сигналов ВНЗ и построения треков являются исходными данными для определения МПЧ и ДЧХ односкачкового мода наклонного распространения 1F2 на радиотрассах в секторе зондирования, минуя коррекцию параметров ионосферы. Для оперативного восстановления параметров ионосферы реализован алгоритм на основе преобразования ДЧХ НЗ в ВЧХ ВЗ вблизи средней точки трассы с последующим восстановлением профиля электронной концентрации, тем самым решается обратная задача ВЗ. В дальнейшем предполагается провести дополнительные исследования по количественной оценки эффективности метода диагностики декаметрового радиоканала по текущим данным ВНЗ на базе автоматизированного программного комплекса обработки и интерпретации ионограмм.

Работа выполнена в рамках базового финансирования программы ФНИ II.12. Результаты получены с использованием оборудования Центра коллективного пользования «Ангара»,