Диагностика параметров магнитореологического гасителя колебаний приборов и станков

В статье представлена методика определения отклонений параметров магнитореологического гасителя колебаний от номинальных значений в реальных эксплуатационных условиях. Приведен расчетный пример определения отклонений параметров гасителя колебаний от номинальных значений.

Применяемые в настоящее время виброизолирующие устройства (ВИУ) предназначены для эксплуатации в ограниченном частотном диапазоне. Отклонения инерционных, жесткостных и диссипативных параметров ВИУ от номинальных значений приводят практически к неработоспособности таких устройств. Поэтому актуальной является задача определения отклонений параметров ВИУ от номинальных значений, т.е. задача диагностики параметров ВИУ. Диагностика параметров рассматривается на примере ВИУ, выполненного на основе магнитореологической суспензии (МРС), так называемого магнитореологического гасителя колебаний (МРГК). МРС относится к классу жидкостей с довольно крупными (10-7 – 10-5 м) частицами дисперсной ферромагнитной фазы. В магнитном поле ферромагнитные частицы, взаимодействуя между собой, образуют так называемые анизодиаметрические агрегаты, ориентированные вдоль силовых линий магнитного поля [1, 2]. При воздействии внешнего магнитного поля МРС изменяет свою намагниченность, что приводит к изменению ее вязкоупругих свойств.

В качестве реального объекта был изготовлен МРГК, представленный на рис. 1, в котором используется обмотка управления, расположенная на подвижном сердечнике. МРС помещается в зазор между подвижным сердечником и корпусом МРГК. При подаче сигнала на обмотку управления происходит изменение вязкоупругих свойств МРС.

Рис. 1. Магнитореологический гаситель колебаний:

1 – корпус, являющийся магнитопроводом;

2 – магнитореологическая суспензия;

3 – подвижный сердечник;

4 – обмотка управления;

5 – плоские пружины;

6 – пружина

МРГК, подверженный силовому вибрационному воздействию, является нормально функционирующим, если ни одна из компонент вектора вибрационного состояния (ВВС) виброизолированного объекта не выходит за пределы установленных допустимых значений, в противном случае МРГК считается неисправным. Диагностика проводится методом параметрического возмущения расчетной модели МРГК при помощи функций чувствительности (ФЧ) [3].

Для получения расчетных числовых значений в качестве ФЧ применяются приближенные стандартные формулы численного дифференцирования. Если для номинального значения параметра qk определить параметрическое возмущение dqk, то для компоненты ВВС zj можно вычислить изменение dzj, соответствующее параметрическому возмущению dqk.

На каждой итерации вычисления ФЧ необходимо решать систему линейных уравнений вида

[A][Z] = [P],                                          (1)

где [A] – матрица системы; [Z] – вектор вибрационного состояния; [P] – вектор внешнего возмущения.

Необходимость решения на каждой итерации уравнения (1)

характеризуется значительными вычислительными затратами, что требует поиска новых методов определения ФЧ, обеспечивающих минимум вычислительных затрат без снижения точности расчета. Только при этом условии возможно создание достаточно эффективного алгоритма диагностики, который рассматривается на основе линеаризованной модели МРГК вида • •                                 •

[M][X] + [B][X] + [C][X] = [P],                   (2)

где [M], [B], [C] – соответственно матрицы инерции, диссипации и жесткости МРГК; [X] – вектор виброперемещения.

Соответствие между векторами [X] и [Z] устанавливается следующими операторными формулами:

• ■

[X] * [Z],

[X] * [Z], [X] * [Z], s             s

где s=jω – комплексная переменная; j – мнимая единица; ω – угловая частота гармонического сигнала.

Подставляя выражения (3) в формулу (2), получаем:

'[M] + И + 1C1 )[Z] = [P],

• V ss

где часть выражения, записанная в скобках, представляет собой оператор матричного преобразования выражения (4) к виду уравнения (1):

• [A] =[M] + [B] + [C],

s s

A где символ = означает равенство по определению.

Дифференцируя уравнение (1) по отношению к параметру qk, получаем матрицу ФЧ ВВС по отношению к параметру qk:

[U Z ] = dZ = - [A] ^{- 1} dA^Z = - AHU A ][Z],   (6)

k   dqk           dqk                 k где введена так чувствительности

называемая матрица параметрической euaj=dA k   dqk

.

Особенность механических колебательных систем по сравнению с электрическими цепями заключается в том, что вектор вибрационного состояния является пространственным и характеризуется, в общем случае, шестью пространственными координатами, причем, как правило, только одна из них является наиболее информативной в отношении амплитуды вибрационного сигнала. Обозначим данную координату как f. Ее можно выделить из пространственного вибрационного сигнала при помощи линейного преобразования f = [D]T[Z],                                            (8)

где [D] – вектор, составленный из единицы и нулей; T – символ транспонирования.

Дифференцируя уравнение (8) по отношению к параметру qk, получаем следующее соотношение:

uf = -df- = [D]Td[Z = [D]T[UZ ].

k dqk        dqk

Подставляя в (9) выражение для ФЧ из уравнения (6), записываем:

Uqk =-[D]T[ArtuAk][Z].

Введем обозначение

[Y]T =-[D]T[A]-1.

Умножим левую и правую части соотношения (11) справа на матрицу [A]:

[Y]T[A] = -[D]T.

С учетом равенства (11) уравнение (10) принимает следующий вид:

uqk = [Y]T[UAk][Z]. (13)

После определения ФЧ несложно по измеренному отклонению амплитуды виброускорения от номинального значения определить отклонения необходимых параметров от номинальных значений, т.е. осуществить их диагностику.

В качестве расчетного примера рассмотрим диагностику параметров для МРГК, динамическая модель которого представлена на рис. 2.

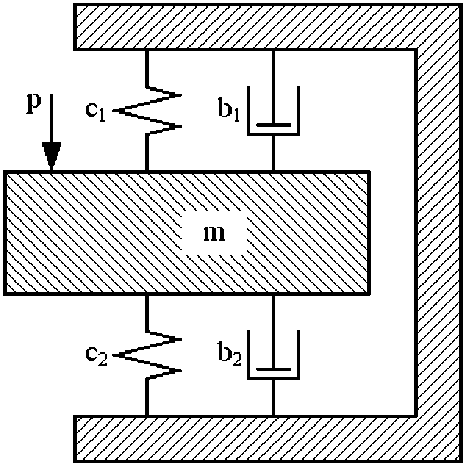
Рис. 2. Динамическая расчетная модель МРГК: m – масса подвижной части;

c1, c2 – коэффициенты жесткости;

b1, b2 – коэффициенты диссипации;

p – внешний гармонический сигнал

Уравнение движения МРГК имеет вид:

mX + bx + cx = p, где x – виброперемещение; b=b1+b2; c=c1+c2.

Запишем уравнение (14) в операторной форме:

• (    b   c)

m •    • , z = p,

• V     s s J

  
  
  
  

где z – виброускорение.

С использованием измеренных значений амплитуды и фазы виброускорения переменные z и p в комплексной форме раскладываются на две известные составляющие:

fz = Z1 + jz2,                                           (16)

.P = P1 + jP2-

На основе уравнения (15) с учетом соотношений подстановки s=jω получаем следующую систему уравнений:

to ²

-1

.to ²

to2m - c)z1 +tobz2 )= p1,

(16) и

to ²m - c ) z₂ -to bz 1 ) = p₂.

Систему уравнений (17) можно привести к виду (1), если ввести следующие обозначения:

[A] = A to2

[Z] =

z1z2

[P]=

to2m - c - tob

tob to2m - c

pp 1.

Lp2 J

Получим диагностические уравнения МРГК для следующих значений параметров номинального режима работы в относительных единицах: ω=1; m=1; c1=1; c2=2,136; b1=1; b2=3,985; p1=1; p2=3,124. Вычислим функции чувствительности компоненты вектора вибрационного сигнала z2 по отношению к параметрам c1 и b2. Матрица [A] уравнения (1) имеет следующий вид:

[A] = 1 2

121 -(1 + 2,136) -1(1 + 3,985)

1(1 + 3,985)

121 -(1 + 2,136)

- 2,136 4,985

- 4,985 - 2,136

Запишем уравнение (1) как "- 2,136 4,985 T Z1" _- 4,985 - 2,136j_z2 _

3,124

Уравнение (12) принимает вид:

[ У 1 У 2 ]

— 2,136

4,985

—I

— 4,985

— 2,136

Решая уравнения (22) [Z] и [Y], получаем:

и (23) относительно компонент векторов

—

[Z] =

[Y] =

—

0,602

0,057 ’

— 0,169

0,072

.

Запишем матрицы параметрической чувствительности для параметров c1

[<] =

[u A₂ ] =

и b2:
d[A] =	— 1	0
dc 1	_ 0	— 1
d[A] =	" 0	1 "
db2	_— 1	0

.

,

Подставим соотношения (24) – (27) в уравнение (13) для определения функций чувствительности компоненты z2 вектора [Z] по отношению к параметрам c1 и b2:

_Uz 2 c₁

— 1

= [Y]^T[U A ][Z] = [ — 0,169 0,072 ] 0

_Uz 2 b ₂

= [Y] T [U A 2 ][Z] = [ — 0,169 0,072 ]

—

0 "	"- 0,602 "
— 1	_— 0,057_
1 "	"- 0,602 "
1 0 _	[— 0,057_

= — 0,098, ⁽²⁸⁾

= 0,053. (29)

На основе результатов, полученных по выражениям (28) и (29), определяются параметрические изменения при измерении отклонений компоненты z2 вектора [Z] от номинального значения:

U Z ² =

c1

_Uz _b 2 ₂

dz2 dc1 dz2 db2

— 0,098,

= 0,053.

Из уравнений (30), (31) определяются отклонения параметров:

dc1 = —

0,098

dz2,

db2 =

0,053

dz2.