Диагностика сложных явлений на основе геометрического анализа изображений

Проблеме разделения изображения на морфологически различные составляющие в последнее время уделяют много внимания в научной среде в связи с её значимостью для важных приложений. Успешные методики для эффективного и точного решения этой задачи могут быть в действительности быть применены к гораздо более широкому кругу областей, в том числе к медицинской визуализации изображений для целей диагностики сложных явлений.

В данном исследовании авторы представили краткий обзор возможностей использования для решения задач диагностики и принятия решений так называемое шиарлет-преобразование (сдвиговое) пространственных данных наблюдений (изображений). Шиарлеты стали частью обширной исследовательской деятельности в течение последних лет для того, чтобы создать новый инструмент для анализа и обработки массивов многомерных данных, которые выходят за рамки традиционного Фурье и вейвлет-анализа [1–7].

Отметим, что хотя проблема разделения морфологических отличительных черт кажется неразрешимой (она неопределенна), так как имеем только одни известные данные (изображения) и два или более неизвестных, в последние годы проведены обширные исследования на эту тему. В монографии [8] положено начало разработке метода разложения изображений, в частности, с применением вариационных методов. Несколько лет спустя, в работе [9] предложен «морфологический анализ компонентов», где показано, что задача разложения может быть разрешима, если есть информация о типе особенностей, которые должны быть извлечены при условии, что морфологические различия между ними достаточно сильны.

Для разделения точки и криволинейной особенности в последнее время теоретически доказано в [2], что ℓ 1 -минимизация решает эту задачу со сколь угодно высокой точностью, предлагая комбинированный набор вейвлетов и кёрвлетов. Вейвлеты обеспечивают оптимально редкое разложение для точечных структур, а кёрвлеты обеспечивают оптимально редкое разложение для криволинейных структур. Следовательно, ℓ 1 -минимизация, применяемая к разложению коэффициентов исходного изображения, преобразует точечные структуры в вейвлеты, а криволинейные структуры в кёрвлеты, таким образом, автоматически разделяя изображение.

Сравнительно недавно появилась новая система представлений, так называемая шиарлет-система (преобразование), она обеспечивает единую обработку непрерывных моделей (изображений), а также цифровых моделей [10–12]. Шиарлет-системы – это системы преобразований, порожденные параболическим масштабированием, сдвигом и оператором параллельного переноса к исходным пространственным данным наблюдений. Это те же вейвлет-системы, имеющие двоичное масштабирование и параллельный перенос функции, однако также включающие в себя характеристику направленности, имея дополнительную «сдвиговою» операцию (анизотропное масштабирование). Эта операция, фактически, дает более удобный подход для анализа направлений, обеспечивая тем самым единую обработку данных, дискретных и непрерывных областей изучаемого изображения [1].

Таким образом, шиарлет является функцией, которая похожа на вейвлет вдоль одной оси и выпукла по другой оси. Шиарлет-преобразование требуют комбинации следующих операторов: оператор масштабирования для создания элементов в различных масштабах; ортогональный оператор, чтобы изменить направление; оператор переноса для перемещения этих элементов в 2D плоскости.

В большинстве многомерных задач важные особенности изучаемых данных сосредоточены в многообразиях малых размерностей. Например, при обработке изображений край – это одноразмерная кривая, на которой интенсивность изображения резко меняется. В последнее время новый подход – система шиар-летов [11–12] предоставила эффективные инструменты для анализа внутренних геометрических черт пространственного сигнала, использующие анизотропные и направленные оконные функции. При таком подходе, направленность достигается за счет применения целых степеней матриц сдвига, а эти операции сохраняют структуру целочисленной решетки, что имеет решающее значение для цифровой реализации. По сути это ключевая идея приводит к единому анализу, как в непрерывной, так и в дискретной области, обеспечивая при этом оптимально редкие приближения анизотропных характеристик.

Как уже упоминалось, шиарлет-системы порождены параболическим масштабированием, сдвигом и оператором параллельного переноса, примененным к исходной пространственной функции (изображению). В работе [10–12] предоставлено описание теории ши-арлет-систем с компактным носителем, то есть систем с отличным пространственным расположением. Следует также отметить, в [11] показано, что большой класс шиарлет-систем с компактным носителем обеспечивает оптимально редкое приближение изображений, управляемое криволинейными структурами. Для шиарлет-преобразования используется дискретное шиарлет-преобразование, реализованное с помощью 2D-свертки с дискретизированными шиарлетами с компактным носителем, алгоритмы представлены в работе [11].

В работе [9] представлен метод разделения изображений «анализ морфологических компонентов», который базируется на редких представлениях изображений. В этом подходе предполагается, что каждое из изображений является линейной комбинацией из нескольких компонентов, которые морфологически различны, например, точки, кривые и текстуры. Успех этого метода основывается на предположении, что каждый из компонентов редко представлен в определенной системе представлений. Основная идея состоит в следующем: в том случае, если такие системы определены, использование алгоритма поиска для редких представлений изображения по отношению к набору, объединяющему все специальные системы представления, приведет к желаемому разделению.

Различные экспериментальные результаты [9] свидетельствуют об эффективности этого метода для разделения изображения без сопутствующего математического обоснования. Математическую основу этого подхода недавно разработали в [2], в которой понятие успешного разделения строго определяется и может быть математически доказано в случае разделения точечных и криволинейных структур, который они назвали геометрическим разделением. Одним из ключевых моментов их анализа является рассмотрение кластерных свойств разреженности, определяемой так называемой кластерной согласованностью.

Результаты аппроксимации, подтверждают, что криволинейные особенности могут быть «разряжено» отображены с помощью шиарлетов. С другой стороны, известно, что вейвлеты дают оптимально разряженную аппроксимацию всюду гладких, кроме сингулярных точек, функций. Следовательно, выбираем полную систему, в которой будем разлагать исходный пространственный сигнал на комбинацию двух следующих систем: ортонормированные вейвлеты Мейера, вейвлеты с ограниченной полосой пропускания, которые задают ортонормированный базис изотропных порождающих элементов; шиарлеты с ограниченной полосой пропускания, направленная и анизотропно плотная система, порожденная шиарлетами с ограниченной полосой пропускания.

Таким образом, теория, изложенная в указанных работах, свидетельствует о том, что задача геометрического разделения может быть успешно решена с помощью комбинированного набора вейвлетов и шиарлетов, с постановкой и решением соответствующей задачи ℓ 1 –минимизации.

В рамках среды Матлаб, разработана вычислительная методика, позволяющая решать задачу обработки сложных медицинских изображений на основе шиар-лет-преобразования (рис. 1, а , б ). Далее приведены результаты обработки данных диагностики уролитиаза.

В диагностике уролитиаза до недавнего времени рентгенологический метод исследования являлся единственным. Однако с внедрением современных технологий лечения пределы возможностей рентгенологического исследования и достаточно частые ошибочные заключения, заставляют искать другие методы диагностики. На сегодняшний день недостаточно только выявить локализацию конкремента, но необходимо определить его плотность и конфигурацию конкремента, оценить функциональное состояние мочевых путей выше и ниже обструкции [13–15].

У больных с уролитиазом, при первичном обследовании у которых не удалось выявить камни в мочевых путях с помощью рутинных методов визуализации, только МСКТ с мультипланарными реконструкциями, позволяет точно определить их локализацию, даже при рентгенонегативных камнях, без применения контрастных веществ [16–17].

Использование современных методов диагностики значительно улучшило результаты лечения больных МКБ. Это связано с уточнением прогностических критериев (локализация, размеры, структура, плотность камня, функциональное состояние верхних мочевых путей и т. д.) в предоперационном периоде. Использование современных методов КТ (СКТ, МСКТ) позволяет детализировать показания и прогнозировать эффективность различных методов лече- ния [14; 18–19]. Например, длительное стояние конкремента в мочеточнике приводит развитию уретери-та с наличием гипергрануляций уретелия. Проведение уретероскопии и контактной литотрипсии в данной ситуации, вследствие инфильтрации тканей и плохой визуализации, чревато высоким риском повреждения стенки мочеточника.

МСКТ с использованием дискретного шиарлет-преобразования путем детализации изображения позволяет выявить рентгенологические признаки этих изменений. Использование лазера при уретерите, наличии грануляций дает возможность производить их коагуляцию, повышая визуализацию конкремента. С помощью гольмиевого лазера удалось раздробить 12 камней, «вколоченных» в устье и 14 камней в средней трети мочеточника. Конкременты небольших размеров (диаметром 0,6–0,7 см) фрагментировались методом холодного дробления. По мере накопления опыта пришли к выводу, что твердые камни лучше дробить с использованием лазерной установки.

Для сокращения длительности операции разработана оригинальная техника дробления крупных конкрементов: в центре конкремента формировалось углубление в виде воронки, диаметр которой должен быть достаточно большим, что обеспечивает лучшую ирригацию, а также предохраняет стенку мочеточника от повреждения. После формирования воронки проводим «холодное» дробление, прикладывая шток ли-тотриптора по направлению от центра к периферии, и производим откалывание небольших фрагментов – диаметром до 0,3 см, которые самостоятельно отходили во время операции или в послеоперационном периоде.

На рис. 2–6 представлены примеры обработки сложных медицинских изображений на основе разработанной методики.

б

Рис. 1. Вид соответствующих окон для выполнения расчетов

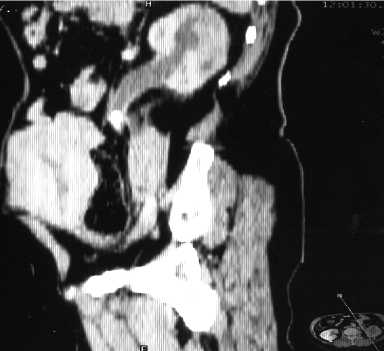
Рис. 2. Решение задачи шумоподавления на снимке

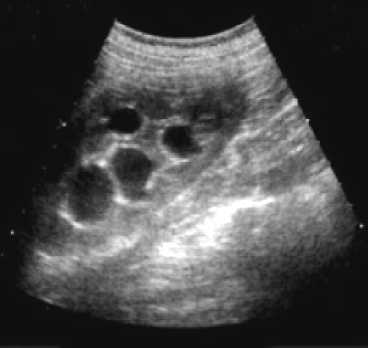
Рис. 3. Ультрасонограмма левой почки: резкое расширение чашечек на фоне обструкции мочеточника

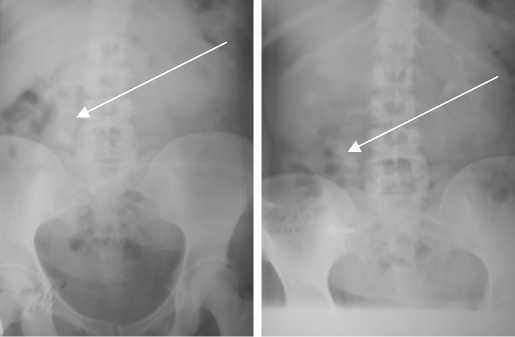
Рис. 4. Обзорная и экскреторная урограмма мочевых путей: тень конкремента на уровне межпозвоночной щели L4 –L5 справа

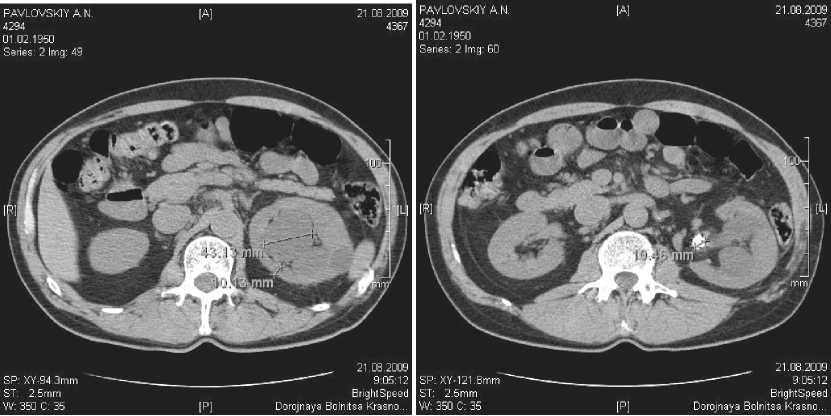
Рис. 5. СКТ: паренхима почки слева однородная с четкими ровными контурами, справа ЧЛС расширена: лоханка до 4,3 см, чашечки до 2,5 см, паренхима неоднородная местами толщиной до 0,5 см., в просвете в/3 правого мочеточника определяется тень конкремента размером 1,5 см, плотностью 1163 HU

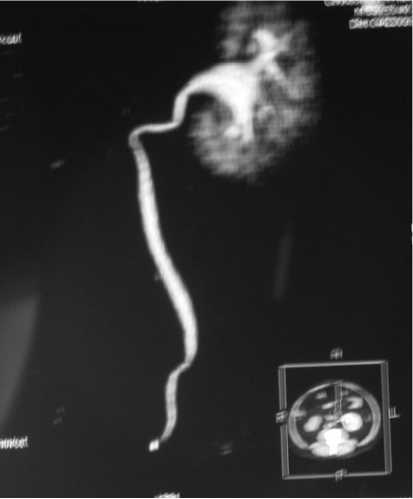
Рис. 6. МСКТ с контрастированием и 3 D визуализацией. Паренхима почки слева однородная, ЧЛС расширена: лоханка до 4,3 см, чашечки до 2,5 см, в просвете н/3 левого мочеточника определяется тень конкремента размером 0,8 см, плотностью 1264 HU

Шиарлет-преобразование позволяет работать с криволинейными сингулярностями, учитывать анизотропные свойства исследуемой среды, причем математический аппарат, применяемый для анализа сложных сигналов тот же для различных физических сред и моделей. Шиарлет-преобразование хорошо применимо для фиксации регулярности изображения в анизотропных средах, учитывает масштаб, пространство и направление. Шиарлет-преобразование эффективный инструмент для анализа внутренних геометрических черт изображения, использующий анизотропные и направленные оконные функции.

В среде Матлаб, на основе разработанной методики, показаны возможности шиарлет-преобразования медицинских изображений для анализа сложных явлений в изучаемой предметной области. МСКТ с использованием дискретного шиарлет-преобразования путем детализации изображения позволяет выявить рентгенологические признаки инфильтрации стенки мочеточника и гипергрануляции уротелия.