Диагностика состояния и реконфигурация управления в механических системах с избыточными силовыми гироскопическими связями

Проблема обеспечения отказоустойчивости и динамической надежности является актуальной для обширного класса механических систем в составе объектов машиностроения, энергетики, аэрокосмической техники и т.д. В отличие от неопределенности либо медленного изменения параметров, полный отказ какой-либо аппаратуры в основном контуре управления принципиально изменяет структуру системы и может привести к возникновению и развитию в ней аварийной ситуации, а далее, если не предусмотрены меры для оперативного блокирования такой ситуации – к катастрофическому поведению системы. В статье представляются методы логико-динамического моделирования управляемых механических систем с возможным нарушением структуры, критерии диагностирования состояния, методы принятия решения об отказе, приемы блокирования развития аварийной ситуации и реконфигурации управления. Приводятся некоторые результаты динамического анализа гиросиловых отказоустойчивых систем управления движением космических аппаратов.

Моделирование логико-динамического управляемого объекта

Обобщенный нелинейный управляемый объект O с вектором состояния

x( t ) ∈ H ⊂ R^{n ν} принимается [1] в виде D ⁺ x( t ) = F ^o (x( t ), u , p ( t ,x), γ _ν ^f ( t )),

• x( t ₀) = x₀; t ∈ T _{t 0} ≡ [ t ₀, ∞ )       (1)

y( t ) = ψ ^o (x( t ), γ _ν ^f ( t ));

z ^o ( t ) =φ ^o (x( t ),y( t ), p ( t ,x)),       (2)

где _D ⁺ – символ правой производной по времени; x₀ ∈ H ₀ ⊂ H ; y( t ) ∈ R ^{r ν s} – вектор измерения состояния объекта, используемый также и для диагностики; вектор-функция z ^o ( t ) ∈ R ^{r ν f} описывает условия возникновения отказов и последующего развития аварийной ситуации; u = { u_j } ∈ U ⊂ R ^{r ν c} является вектором управления, а p ( t , x) ∈ P – век-тор-функцией параметрических возмущений в классе P . Вектор логических переменных γ _ν ^f ( t ) ∈ B ^m ≡ B × B × ⋅⋅⋅ × B , B = (0,1) является выходом асинхронного логического автомата (АЛА) A ^f с памятью для генерации возможных отказов

γ _ν ^f = δ ^f ( κ _ν ^f , l _ν ^f ) ;

f       f ff f f       f f

κ _{ν+ 1} = λ ( κ _ν , l _ν ), κ _ν ≡ κ ( ν ), κ ₀ = κ (0);

l ν ^f ≡ l^f ( ν ) = g^f (z ^o ( t ν ^f )),        (3)

где tνf – моменты времени возникновения отказа и развития аварийной ситуации, причем автоматное время ν ∈ N0 ≡ [0,1,2,...) связано с непрерывным временем t соотноше-f f f       f f ff нием t = tν + (τ    tν ) ; τ ∈ τν ≡ [tν ,tν+1) , вектор lνf (t) = const ∀t ∈ τνf и изменение логического вектора γνf в общем случае приводит к изменению размерностей векторов x(t) и y(t) в моменты времени t = tνf при нелинейных непрерывных отображениях f  xf    f  yf

x( t _ν+ ) = P _ν (x( t _{ν -} )) и y( t _{ν +} ) = P _ν (y( t _ν- )) .

Задачи диагностикии реконфигурации управления

Пусть заданы фиксированные кратные периоды дискретизации T_u , T_q ≤ T_u и T_r ≥ T_u соответственно управления, измерения и реконфигурации. Будем использовать обозначения x _k = x( t_k ); t_k = kT_u ; t_s = sT_q ; t _µ = µ T_r и x^f _k = F _{T u} (x _s ), x _µ ^f = F _{T r} (x _k ), где x^f _k является значением переменной x _s , измеренной с периодом дискретизации T_q и отфильтрованной к моменту времени t_k , а F T_y ( ⋅ ) – оператором цифровой фильтрации с периодом дискретности T_y , y = u,r . Пусть также заданы подсистемы дискретного измерения состояния управляемого объекта O и цифровой фильтрации доступных измерений:

• _•    для диагностики состояния объект а y ^d s =ψ ^d (y s );z k ^{d f} = F T_u (y s ^d),

k , s ∈ N₀;                (4)

• _•    для формирования управления и его реконфигурации

y ^u _s =ψ ^u (y _s );      y^f k = F T_u (y s ^u);

z^f µ = F T_r (z k ^{d f}),            µ , k , s ∈ N₀ .    (5)

Основные задачи диагностики и реконфигурации управления состоят в синтезе:

• _•    синхронного логического автомата (СЛА) A d с памятью для диагностики объект а

γ k ^d =δ ^d ( κ k ^d , l k ^d );         κ k ^d + 1 =λ ^d ( κ k ^d , l k ^d ),

κ 0 ^d = κ ^d ( t 0 ) ,                    (6)

с логическими векторами состояния κ _k ^d , входа l_k^d = g^d (z _k ^{d f})и выхода γ _k ^d ;

• _•    синхронного логического автомата A ^r реконфигурации, также с памятью, для описания процессов блокирования аварийной ситуации и реконфигурации контура управления

r r rr        r     r rr

γ _µ =δ ( κ _µ , l _µ );       κ _{µ+ 1} =λ ( κ _µ , l _µ ),

κ 0 ^r = κ ^r ( t 0 ) ,                  (7)

при логических векторах состояния κµr , вхо-r r f df        df             d                      r да lµ =g (zk,γµ ) с γµ =FTr(zk) и выхода γµ;

• _•    нелинейного закона управления

u k = ^{U (x}e k ,y^f k ,У о k ^, Y^ );

x ek+1 = Fe(x ek,yfk ,У o, uk , Y 4 , Y^ ), xeO = xe(t0), Ц, k e N0,           (8)

где yfek =FTu(ψeu(yes)); yes =ψeo(xes,γkd)и вектор xes ∈ Rnµe является вектором состояния упрощенной дискретной модели объекта xes+1 = Fe(xes,uk,γkd,γµr) ;

x_e0 = x_e( t ₀),                 (9)

вектор x , = x (t,) e Rnм представляет его ek      e k оценку, размерность nµe ≤ n = max{nν } и вектор yok представляет программное движение по выходу, с его реконфигурациями в соответствии с выходными сигналами СЛА Ar .

Замкнутые логико-динамические контуры (4) – (9) предназначены для отказоустойчивого управления объектом (1) – (3).

Синтез логическихавтоматов диагностики

В наиболее совершенных механических управляемых системах, например в системах управления движением (СУД) космических аппаратов (КА) информационного назначе- ния – связи, навигации, наблюдения за объектами на поверхности Земли, применяется трехуровневая логическая система, реализованная с помощью бортовой вычислительной техники:

• 1.    на нижнем уровне – СЛА A_d ^d , встроенные непосредственно в бортовые приборы для автоматического мониторинга их состояния на основе измерения и оценки физических переменных (токов, напряжений, механических перемещений, скоростей и т.д.);

• 2.    на среднем уровне – СЛА A_c ^d для диагностики состояния каналов управления (рыскания, крена, тангажа, контура управления панелями солнечных батарей и т.д.);

• 3.    на высшем “системном” уровне – СЛА A ^d для глобальной диагностики СУД КА.

На двух последних уровнях функциональная диагностика выполняется на основе сравнения выходных сигналов моделей нормального и фактического функционирования с использованием эталонных моделей [2].

Результаты анализа процесса диагностики состояния СУД, проводимого специалистами центра управления полетом КА, указывают на высокую эффективность методов, основанных на использовании детальной информации о приборах, алгоритмах управления, законах движения КА и множестве других элементов процесса его функционирования, а также некоторых инвариантных соотношений между переменными состояния системы. Неисправность СУД проявляется в рассогласовании характеристик процессов управления реальной системы и ее эталонной модели на величину, превышающую априорно известные ошибки измерений датчиков и отработки управляющих воздействий исполнительными органами. Характер и значения указанных рассогласований позволяют выдвинуть конечное число гипотез, объясняющих неисправность с глубиной, достаточной для принятия решения по управлению резервами. Каждой гипотезе соответствует определенная ветвь АЛА Af (3), описывающая возникновение отказа и развития аварийной ситуации в объекте (1), (2). Для каждой такой ветви сначала с помощью инженерных методов разрабатывается логическая таблица истинности процесса контроля, на основе которой далее стандартными компьютерными методами синтезируется соответствующий СЛА диагностики. Конкретный пример построения простейшего СЛА диагностики состояния СУД КА в виде логической функции выбора представлен в [3].

Диагностика с использованием критерия Вальда

Для реализации схемы локализации отказов СУД на программном уровне в БЦВМ необходимо решить задачу выбора информативных параметров. Очевидно, что с уменьшением числа контролируемых параметров процесс диагностики упрощается. Алгоритм диагностики СУД по ее эталонной модели, работает в фоновом режиме, т.е. в процессе управления движением КА. При этом аномальная ситуация выявляется посредством вычисления вектора невязок между измеренными (X) и модельными (Хm) параметрами:

Поведение параметров контроля ej, j=1, 2, во времени можно рассматривать как случайный процесс, характеристики которого зависят от множества факторов. К ним, в частности, относятся, ошибки измерения; погрешности отработки управляющих воздействий; погрешности моделирования динамики движения вследствие упрощения модели; неточности знания конструктивных параметров КА, возмущающих воздействий и т.д. В этом случае следует проводить классификацию не мгновенных значений невязок ejk, а некоторого случайного процесса, представленного дискретной последовательностью значений ejk n, где k=1, 2…n. Каждое из этих значений предъявляется для анализа в соответствующие моменты времени tk . Классификация такого случайного процесса может быть осуществлена с помощью математического аппарата последовательной проверки гипотез, в частности, на основе последовательного критерия отношения вероятностей Вальда (ПКОВ) [4, 5], который обладает важ- ными свойствами:

сходимостью с вероятностью 1, следовательно выбором пороговых значений α и β можно обеспечить любой априорно заданный уровень погрешности классификации;

не требует независимости и равенства распределений вероятностей классифицируемых случайных векторов;

обеспечивает минимизацию среднего числа наблюдений, необходимых для достижения заданного уровня достоверности оценки, и минимизацию среднего объема хранимой в процессе классификации информации, что значительно упрощает его реализацию в бортовом программном обеспечении СУД.

Процедура анализа с помощью критерия Вальда реализуется следующим образом. Для каждого значения невязки параметров вычисляется вектор логарифмического отношения правдоподобия:

λ j_k = – ln (P(ej_k/ W₁) / (P(ej_k/W₂)), (11) где ej_k – значение вектора ej на k-ом шаге вычислений; P(ej_k/W_j) – функция условной плотности вероятностей ej_k при фиксированном событии, состоящем в том, что ej_k принадлежит классу j=1, 2. Величина λ j_k также является случайной. Поэтому для независимого распределения ej вектор суммарного логарифмического правдоподобия после n наблюдений с учетом (10) и (11) равен:

L= – ln{P[(e11,e12...e1n)/ W1]/

P[(e21,e22...e2n)/W2]} = nn =-∑ln { P[(e1k)/W1] / P[(e2k)/W2]} =∑λjk, 11

(12) где k=1,2,…n – номер шага контроля; W₁ и W₂ – классы состояния системы (соответственно “норма” и “не норма”). Решающее правило ПКОВ состоит в покомпонентном сравнении вектора L (12) с фиксированными границами α и β этого критерия и имеет вид:

L ≤ α → е_1n ∈ W1 ,

α << L <<  β ??? (обработку измерений продолжать)

β ≤ L → е _2n ∈ W2 .

Синтез логического автомата реконфигурации управления

Процесс восстановления работоспособности СУД КА включает следующую последовательность действий:

• 1.    исключение неисправного прибора из контура управления;

• 2.    анализ наличия резерва у отказавшего прибора, в том числе функционального в отношении СУД;

• 3.    подготовка и включение резервного прибора в контур управления или реконфигурация СУД в случае применения функционального резерва;

• 4.    восстановление ориентации КА;

• 5.    формирование информации о готовности СУД к выполнению целевых задач КА.

Результаты определения неисправного прибора поступают в блок управления восстановлением работоспособности в виде СЛА A ^r реконфигурации. Набор стратегий восстановлением работоспособности СУД (переключение на структурный или функциональный резерв, последовательность изменения режимов работы, восстановление ориентации и т. п.), соответствующих возможным отказам приборов СУД, реализуется на программном уровне в БЦВМ. Выбор алгоритмов реконфигурации осуществляется на основе инженерных методов и, как правило, индивидуален для конкретного класса КА. Для каждого вида отказов приборов СУД и их комбинаций составляются логические таблицы истинности, а затем компьютерными методами синтезируется СЛА A ^r реконфигурации.

Отказоустойчивое гиросиловое управление ориентацией КА

Возможности обеспечения отказоустойчивости гиросиловых СУД с избыточным числом гиродинов фактически определяются на этапе проектирования. Здесь важную роль играет выбор схемы силового гироскопического комплекса (СГК) и его расположения относительного строительных осей КА. В СГК класса 2-SPE на рис. 1 на основе четырех гиродинов один гиродин (№4) находится в “холодном” резерве, все

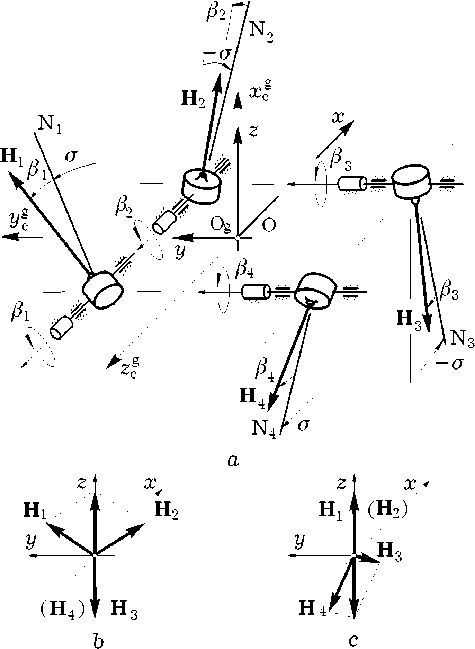
Рис.1. Схемы силового гироскопического комплекса

гиродины имеют возможность изменять положение вектора собственного кинетического момента H _p в диапазоне ± 90 ° от базового направления N _p , p = 1:4, см. рис. 1 a . При отказе любого одного гиродина в этой схеме соответствующая реконфигурация СГК полностью нейтрализует такую аварийную ситуацию, см. рис. 1 b и рис. 1 c . [6]

Большой степенью отказоустойчивости обладает схема СГК типа 3-SPE на основе шести гиродинов, распределенных в три пары (рис. 2). Данная схема не имеет “холодного” резерва, но остается работоспособной при отказе любых трех гиродинов [7]. Рис. 3 демонстрирует зависимость динамических свойств СГК класса 2-SPE на рис. 1 от его расположения на корпусе КА, а именно переходные процессы по углу тангажа при отказе ГД №3, рис. 3 a и 3 b – при совпадении оси x _c^g СГК со строительными осями КА Oz и Oy соответственно [6].

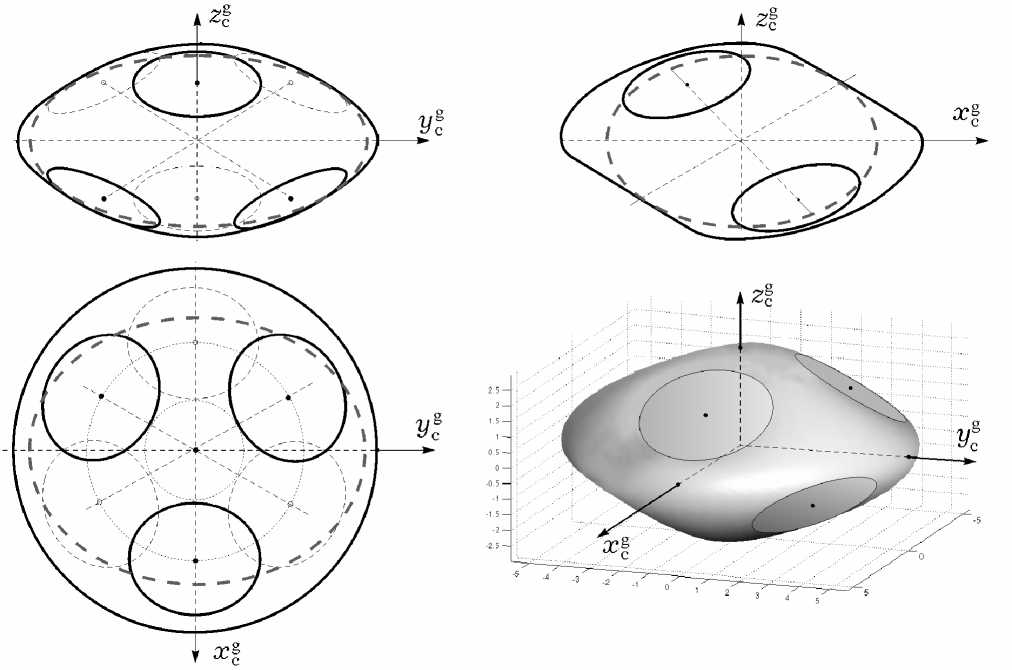
Рис. 2. Область вариации вектора кинетического момента схемы 3-SPE

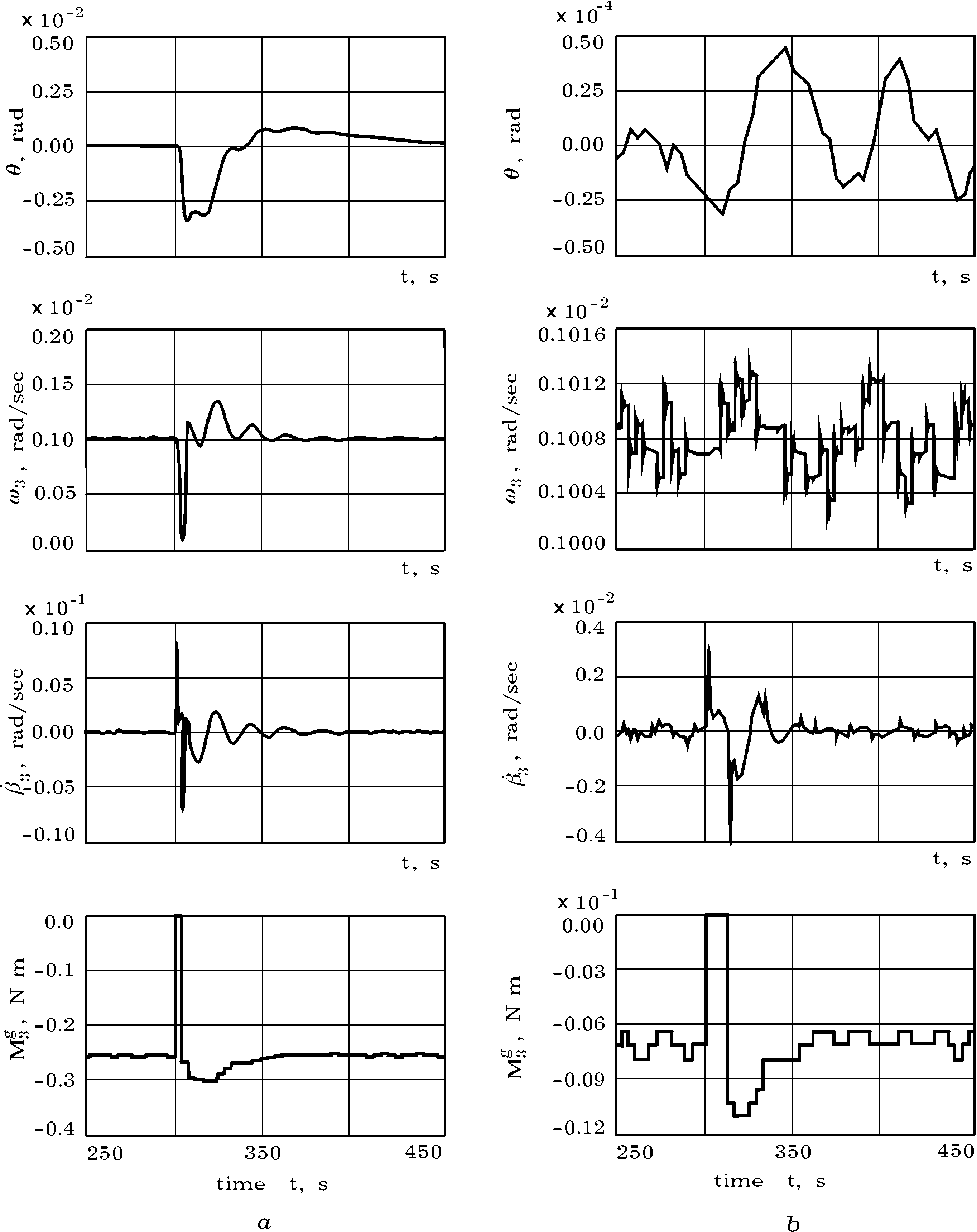
Рис. 3. Переходные процессы при отказе гиродина №3 в схеме 2-SPE

Заключение

Представлены приемы логико-динамического моделирования развития аварийных ситуаций, критерии диагностирования состояния, методы последовательной классифика- ции отказов приборов в контуре управления и реконфигурации управления в механических системах с избыточными гироскопическими связями. Приводятся некоторые результаты анализа гиросиловых отказоустойчивых систем управления ориентацией космических аппаратов. Полученные результаты эффективно использованы практически при создании гиросиловых отказоустойчивых систем управления ориентацией многих российских космических аппаратов [1], [8-10].

Работа поддержана РФФИ (04-01-96501 и 05-08-18175), Президиумом РАН (программа фундаментальных исследований 22) и Отделением энергетики, механики, машиностроения и процессов управления РАН (программы 16 и 18).