Диагностика стохастического ионосферного канала в декаметровом диапазоне радиоволн

Для обеспечения надежности и помехоустойчивости ионосферного радиоканала важно иметь априорные сведения о его физических параметрах и свойствах [Благовещенский, Жеребцов, 1987; Rawer,

1993; Благовещенский, 2011]. При распространении сигналов в реальной случайно-неоднородной ионосфере эти сведения известны с определенной долей вероятности. С другой стороны флуктуации характеристик пробного сигнала, прошедшего через ионосферный канал, несут в себе информацию о случай- ных неоднородностях среды. Поэтому для надежного использования ионосферного канала полезна диагностика ожидаемых характеристик основного сигнала, направленного в пункт назначения, по данным измерений характеристик встречного пробного сигнала, принятого в пункте излучения основного сигнала. Одним из вариантов решения этих вопросов является подход, базирующийся на прямой диагностике ионосферного радиоканала, когда параметры пробного зондирующего сигнала пересчитываются в характеристики основного передаваемого сигнала [Куркин и др., 1993]. При этом получены важные результаты, касающиеся прогнозирования максимальноприменимых частот и дистанционно-частотных характеристик декаметрового сигнала в различных геофизических условиях. Точность оперативного прогноза, основанного на прямой диагностике радиоканала, во многом зависит от строгости функциональных соотношений, связывающих характеристики пробного и передаваемого сигналов. В основном такие соотношения получают для регулярной среды без учета ее тонкой хаотической структуры, поэтому интерес представляет вывод подобных соотношений в задаче распространения сигнала в случайнонеоднородной ионосфере.

В общем случае декаметровый ионосферный радиоканал представляет собой сложную многосвязную систему [Mitra, 1947; Davies, 1990]. Вследствие существенной анизотропии ионосферы, многомас-штабности неоднородностей и особенностей механизмов распространения радиоволн диагностика ионосферного канала представляет большую проблему и весьма актуальна [Казанцев и др., 1967; Благовещенский, Жеребцов, 1987; Куркин и др., 1993; Алимов и др., 1997; Крюковский и др., 2012, 2016; Ипатов и др., 2014; Бова и др., 2019]. В частности, при оценке статистических характеристик декаметрового сигнала встает вопрос о форме спектра случайных неоднородностей канала. Нет полной ясности о пространственном распределении неоднородностей по всей толще ионосферы. Между тем, решение задачи оценки статистических характеристик декаметрового сигнала в ионосферном радиоканале возможно с использованием модели случайнонеоднородной ионосферы с обобщенными (интегральными) свойствами. В данном направлении были получены важные результаты благодаря введению представлений об эффективном корреляционном эллипсоиде, приближенно описывающем случайные неоднородности среды [Гусев, Овчинникова, 1980; Вологдин и др., 2007, 2012; Афанасьев и др., 2009] и позволяющем существенно упростить аналитические расчеты статистических моментов сигнала. Несмотря на то, что ионосфера является многомасштабной случайно-неоднородной средой и характеризуется степенным спектром неоднородностей, в ряде случаев при расчетах низших моментов траекторных характеристик сигнала можно использовать гауссов корреляционный эллипсоид неоднородностей с эффективными параметрами. В частности, исследования [Алимов и др., 1997; Афанасьев и др., 2009; Afanasiev et al., 2010] показали, что при расчетах дисперсии фазы декаметрового радиосигнала в многомасштабной случайно-неоднородной среде можно использовать гауссову модель корреляционного эллипсоида, если в качестве пространственного масштаба неоднородностей считать внешний масштаб ионосферной турбулентности, заданной степенным спектром. Связано это с тем, что высокочастотная часть спектра неоднородностей в большей степени оказывает влияние на амплитуду сигнала и в меньшей степени на его фазу [Ishimaru, 1999].

В работе [Агеева и др., 2020] была рассмотрена возможность оценки статистических характеристик сигнала в двумерном информационном канале по данным измерений траекторных моментов пробного сигнала. В настоящей работе этот подход развит на трехмерный случай и применяется для расчета ожидаемых статистических характеристик декаметровых сигналов на односкачковых ионосферных трассах.

ОСНОВНЫЕ ТЕОРЕТИЧЕСКИЕ СООТНОШЕНИЯ

Пусть в пункте I₀, расположенном на поверхности Земли (рис. 1), находится источник квазимоно-хроматического декаметрового сигнала. Оценим ожидаемые статистические траекторные характеристики сигнала на заданной ионосферной трассе I 0 P 0 , (длина трассы x к ) С этой целью из некоторого пункта I v , расположенного в окрестности P 0 , направим пробный сигнал в направлении на источник основного сигнала. Будем считать, что траекторные характеристики пробного сигнала могут быть измерены в пункте P v , совпадающим с I 0 . Получим приближенные аналитические соотношения, связывающие статистические траекторные характеристики сигналов на основной трассе I 0 P 0 и вспомогательной трассе I_vP_v (длина трассы x _p) Рассмотрим случай распространения сигналов в случайно-неоднородной ионосфере без учета магнитного поля Земли и кривизны земной поверхности. Эти упрощения нам необходимы, чтобы на первом этапе решения поставленной общей задачи более наглядно и явно продемонстрировать потенциальные возможности предлагаемого приближенного метода оценки ожидаемых статистических характеристик сигнала на одно-скачковой трассе средней протяженности.

В качестве измеряемых характеристик пробного декаметрового сигнала, излученного из пункта I v и принятого в пункте излучения основного сигнала I 0 , будем использовать вторые статистические моменты фазы, групповой задержки и доплеровского смещения частоты. Для восстановления параметров корреляционного эллипсоида неоднородностей ионосферы по данным измерений характеристик пробного сигнала на вспомогательной трассе I v P v получим связы-

Рис. 1. Схема диагностики ионосферной трассы I0P0 по данным измерений на трассе IvPv вающие их функциональные соотношения с учетом граничных условий в пунктах приема и излучения. В лучевом приближении [Кравцов, Орлов, 1980] для флуктуаций фазы, групповой задержки и допле-

ровского сдвига частоты сигнала, распространяющегося в изотропной трехмерно-неоднородной ионосфере, в декартовой системе координат имеем [Гершман и др., 1984]

xp

2n f            ( dy 1    ( dz 1

Ф = —— Ve 1 + 1 I + 1— I dx,(1)

c О         V dx) V dx )

( dy Y ( dz Y

+I I +I I dx,(2)

V dx ) V dx )

xp t—J 4 J1

^x p      22

f д            ( dy 1    ( dz 1

A f — —            e 1 +I I +I I dx ,         (3)

c дт      у   V dx ) V dx )

функция ε₀ описывает среднюю диэлектрическую проницаемость радиоканала; ε 1 характеризует пространственно-временные случайные неоднородности ионосферы.

Из практики декаметровой связи известно, что в спокойных геофизических условиях при наклонном зондировании ионосферы радиоволны обычно распространяются в плоскости дуги большого круга [Rawer, 1993] . Поэтому будем полагать, что волновое поле более регулярно в поперечной плоскости, чем в вертикальной. Для простоты рассмотрим среднюю траекторию луча, лежащую в плоскости дуги большого круга (в нашем случае в плоскости XOZ (α₀=0, y ₀=0)). Подставляя разложения (5) в (1)–(4) и выполняя вычисления с учетом граничных условий в пунктах приема и излучения, получаем по-

рождающие уравнения

где ε=ε( x , y , z , τ) — пространственно-временная случайная функция диэлектрической проницаемости; τ — время; f — рабочая частота; c — скорость света; x _p — дальность вспомогательной трассы, а интегрирование проводится вдоль случайных лучевых траекторий, соединяющих пункты излучения и приема пробного сигнала. Хорошо известны различные способы построения лучевых траекторий [Казанцев и др., 1967; Кравцов, Орлов, 1980; Кляцкин, 2008; Крюковский и др., 2012] . Для расчета лучей мы используем систему дифференциальных уравнений в эйлеровой форме с независимой переменной элемента дальности dx [Терещенко, 1971]

dz

— ^— ctg ^e dx

dy

— — tga dx

^x p 2

^{2n f}             ( d^z o I

Фо —-----IV8oA 1 + It- I dx, c о         V dx )

x p 2

t0 — i -^.1 + 1 d-° I dx,

Оо С^о V V dx )

af ———Ap VeTa 1 + (dz°-1 dx — 0(8)

о                     о I dx I c * о и уравнения для флуктуаций

Ф1—n—    -d^ •(9)

c ₀ ε ₀ sinβ ₀

x p

d e    i /      _{2    2} \ ( д ve        д ve 1

— — —/=(1 + sin вtg a) ----ctge--I dx Ve                V дx        дz )

t ₁

c Ve e smp_o ^д z о

F p C x)     д Б!

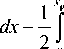
dx ,

^{ε 1}       dx , (10)

c ε₀ε₀sinβ₀

d a     1 /         2        ₂ \

— — —/=(1 + cos a ctg в ) dx ε

(Vе

V ^д У

д ve

^— —tg^a д x

a f — — — I         д Б 1

где x , y , z — текущие координаты луча; α, β — углы рефракции в азимутальной и угломестной плоскостях. По сравнению с лучевыми уравнениями в гамильтоновой форме [Агеева и др., 2020] , где независимой переменной является элемент групповой задержки, эйлерова форма позволяет более компактно и наглядно представлять результаты расчетов характеристик наклонного распространения радиоволн в случайно-неоднородной ионосфере.

Статистические моменты траекторных характеристик пробного сигнала на вспомогательной трассе I v P v определим в приближении метода малого параметра [Арнольд, 1989] . Для функций, входящих в уравнения (1)–(4) используем разложения

где

^F p⁽ x ) ^— F 1p⁽ x ) ^{+ F} 2p⁽ x ),

F 1p ( x ) —

с

2sinβ_p R _1p( x _p)

R 2p ( x ) P 1p ( x ),

^F 2p ⁽ x ) ^—

с

2sinβ_p R _1p( x _p)

R 1p ( x ) P 2p ( x ),

x

P4 x ) — J

sin в _о д е _о

ε ₀

^д z о

R 1p ^{( x} )

dx c ε0

P 2p ( x ) — x p s ⁱ nA’ I^е! R 2_P ( x ) - d L,           (16)

^J:   ^еО    ^д z О         c 4о

^{e — e}0^{( z} ) ^{+ e}1^{( x} , У , ^z , ^т)

Ф ^— Ф о ⁺ Ф 1 , t ^— t 0 ⁺ t 1

‘Af — Af0 +A f z — z о + z 1, У — У о + У1 ,P — во + в1, a — ao + ap

R i — -^ ^{Z o}- ( x ),    R₂ — А^о_ ( x — x )

^1p    д в _р          ^2p    д в _р    ^p

фундамен-

где y ₀, z ₀, α₀, β₀, φ₀, t ₀, Δ f ₀, y ₁, z ₁, α₁, β₁, φ₁, t ₁, Δ f ₁ — средние и флуктуационные характеристики сигнала;

тальные решения краевой траекторной задачи для пробного источника; β p — угол входа пробного сигнала в канал (отсчитывается от вертикали), индекс p характеризует пробную трассу. Интегрирование в (6)–(11), (15), (16) проводится по средней траектории, являющейся решением системы уравнений

{ ^ = ctg в о , d = - 4- '               (17)

L dx          dx     Je ₀ о z ₀

с начальными условиями z 0 ( x p )=0, β 0 ( x p )=β p .

На основе (9)–(11) получим статистические моменты траекторных характеристик пробного сигнала на вспомогательной трассе протяженностью x p . Рассмотрим условия квазиоднородного случайного поля неоднородностей канала. Функцию корреляции флуктуаций диэлектрической проницаемости ионосферы зададим в виде [Гершман и др., 1984]

N ^- (^£1 ( x 1 , У 1 , ^Z 1 ^,T1 ) ^£1 ^{( X} 2 , У 2 , ^Z 2 ^,T2 )) = N 1 N 0 , ⁽¹⁸⁾ где N 0 — однородная часть корреляционной функции. Функция N 1 характеризует статистическую неоднородность случайного поля неоднородностей и учитывает непостоянство параметров неоднородностей в канале, причем функция N 1 изменяется более медленно, чем N 0 . В качестве функции N 1 рассмотрим зависимость N ₁ =μ²(1–ε₀)², где μ² — интенсивность случайных неоднородностей электронной концентрации ионосферы. Движение неоднородностей учтем в рамках гипотезы о замороженном переносе:

N о = exp I- -1 2- [ ( X - x 2 ) 2 + ( У 1 - y 2 ) 2 +

^V a                                  (19)

^{+ ( Z} 1 — ^Z 2 — ^{V ( T}1 — ^T2 ) ) ] ) ,

где

2     ^x p

J 1 - y® f

⁴ c sin ^ep о

^J 2 ^-

^J 3 ^-

где a — масштаб неоднородностей; V

— скорость

движения случайного поля неоднородностей. Составляя из (9)–(11) статистические моменты и проводя аналитические преобразования, для выбранной модели функции корреляции неоднородностей по-

лучаем интегральные выражения для траекторных характеристик сигнала

дисперсий

σ ² φp

x p

- f

ли ² a ц ² (1 — £₀ ) ² dx 4 c ² ε₀sinβ_p

2 f p

x p

- f

f ² PP V 2 Ц^{2 (1 —} E o^{) 2} sin ^в

2 a

c ²ε₀

⁰ dx

° A Z p

x p

₊ x ^p УП a ц ^{2 (1 —} £ о ) ^f 4 c ^{2   £} 0 sin^

² Ц ² (1 — £₀ ) 2 . 2 _o 7П ,

2 • _n sin ^Sp    dx^{X +}

ε ² ₀sinβ₀          ac ²

⁾ dx ,

где ω=2π f . Решая уравнения (20)–(22) относительно неизвестных параметров корреляционного эллипсоида, получаем

ц ² - * J °

—

3 σ ²φp

a -

А Z p

—

φp

2 , 3φp

(1 — £ ₀ )² dx

,

ε ₀

V -. --------:

J 4( J 1σ

σ f p J 1 J 2

А Z p

2 , 3φp

2sinβ _p π c ²

π 4 c ² sinβ

x p f 0

x p

f

(1 — £ 0 )² F p ² dx

ε 3₀          ,

(1 — £ ₀ )² dx

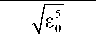
J =   f ²УП ^{x p} sin² в 0 (1 — £ 0 )² dx

⁴   2 c ² sin ^ep ^f         7Ё 0

.

Важно отметить, что интегралы J ₁, J ₂, J ₃, J ₄ не зависят от параметров корреляционного эллипсоида неоднородностей и формируются только средними траекторными характеристиками пробного сигнала на трассе I v P v , зависящими от свойств диэлектрической проницаемости усредненной ионосферы ε 0 .

Определив параметры эллипсоида на вспомогательной трассе I_vP_v, можно рассчитать ожидаемые статистические характеристики основного сигнала на заданной трассе I 0 P 0 . Используя тот же математический аппарат, что и выше, для моментов траекторных характеристик основного сигнала на трассе I 0 P 0 получаем

φ

x к \nw aц (1 — £0) d

0    4 c   ε₀sinβ_n^,

° f ^-

I

f²PV V ²ц ^{2 (1 — £} 0 ^{) 2 si}n^e 0

2 a

c ² ε₀

dx ,

° 2 , ^{- 2} J [ ^{F ( x} ) ] ^{2 Ц (1} • ^£_R⁰ ) sin ^{2 e} n -^4 ^{dx +} ₀          ε₀ ² sinβ₀          ac ²

+ ^x jA . Ц211-Е,)² dx ,

₀ 4 c ² ε ³ ₀sinβ₀

где

F ( x ) - F 1 ( x ) + F 2 ( x ),                                (33)

с —              P (vA P(yA	(34)
F ( x )                       2 ( x ) F ( x )’ 2sm e n R 1 ( x k ) с
	(35)
F ,( x ) - 2sinp . 1Ц xK ) R 1( x ) P 2 (x )’ P 1 ( x ) - ( iin-S i ^£0 R H x , 00   £0    5 z 0 c ^£ 0
	(36)
p 2 ( x ) - x k iin-B i ^ R 2i x i dx. Jx   £0    5 z 0 c ^£ 0	(37)

^ - —-(x), R - —-(x — x) — фундаменталь-1 ав„ 2 apn к ные решения краевой траекторной задачи для основного источника, βn —угол входа основного сигнала в канал, индекс n характеризует заданную трассу. Интегрирование в (30)–(32), (36), (37) про-

водится по средней траектории, являющейся решением системы уравнений (17), с начальными условиями z 0 (0)=0, β 0 (0)=β n .

Подставляя найденные параметры корреляционного эллипсоида (23)–(25) в (30)–(32) и проводя аналитические преобразования, имеем:

σ φ2	G 1   2 T О ФР , J 1			(38)
σ2 f	G 4  2 — r 0 f p , J 4			(39)
о Д t	— GT- О Д t p + о фр I J 2	' G L . J i	- G 2 J 3 ) J 2 J 1 J	(40)

где

_  ^_M 2 x к (1 - £ 0 )² dx

G^{1 —} 4 ^ 2^ in₽ r J ^/^,

G 2 =

2 sin p _n 7Л x ? (1 — £ 0 ) 2 F 2 dx

^J                           ,

G 3 =

Vn     x ? (1 - £ ₀ )² dx

4 c ² sin P_n ^J     _A/Z5

n 0         ε ₀

G 4 =

f ² π ^xк

² c 2 sin P n ^J 0

sin² p _o (1 - £ ₀ )² dx

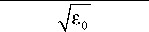
Здесь интегралы G 1 , G 2 , G 3 , G 4 зависят только от свойств диэлектрической проницаемости ε 0 и формируются траекторными характеристиками основного сигнала на трассе I 0 P 0 в усредненной ионосфере.

Соотношения (38)–(40) определяют явную связь статистических характеристик основного и пробного сигналов на трассах наклонного зондирования ионосферы. Проводя измерения о ф_р , o f , о Д пробного сигнала на вспомогательной трассе I_vP_v и задавая средний высотный профиль диэлектрической проницаемости ионосферы ε 0 , формулы (38)–(40) можно использовать для расчетов ожидаемых статистических траекторных характеристик сигнала на заданной трассе I 0 P 0 .

АЛГОРИТМИЗАЦИЯ РАСЧЕТНЫХ ФОРМУЛ

Для количественных оценок о ф , o f , о Д t на основе (38)–(40) необходимо вычислить интегральные коэффициенты (26)–(29), (41)–(44). Непосредственный численный расчет достаточно сложен, поскольку необходимо знать все подынтегральные функции, включая фундаментальные решения, вдоль средних траекторий на основной и вспомогательной трассах. Между тем, полагая верхние пределы интегралов (26)–(29), (41)–(44) переменными и дифференцируя интегралы по этим пределам, получим дифференциальные уравнения, которые можно численно проинтегрировать совместно с системой уравнений (17). Проводя указанные преобразования, для расчета (26)–(29), (41)–(44) имеем следующие дифференци-

альные уравнения:
dJ 1	Vnto2	(1 - £ 0 )2	(45)
dx	4 c 2 sinβ p	ε 0 ,
dJ 2 dx	2sin P p д/Л (1 - £ 0 )2 F p 2 —      c 2                    ’ ε 0		(46)
dJ 3	π	(1 - £ 0 )2	(47)
dx	4 c 2 sinβ p	ε50 ,
dJ 4	— f2 ^	si n2 P 0 (1 - £0 ) 2	(48)
dx	2 c 2 sinβ p	ε0           ,
dG 1	— Vnto2	(1 - £ 0 )2	(49)
dx	4 c 2 sinβ n	ε0 ,
dG 2	2sinβ n	П (1 - £ 0 )2 F2	(50)
dx	—      c 2	ε30          ,
dG 3	π	(1 - £ 0 ) 2	(51)
dx	4 c 2 sin β n	ε50 ,
dG 4	— f 2 7л	si n2 P 0 (1 - £0 ) 2	(52)
dx	2 c 2 sin β n	ε 0

c начальными условиями:

J 1 ( x p ) = 0, J 2 ( x p ) = 0, J з ( x p ) = 0, J 4 ( x p ) = 0,

G 1 (0) = 0, G 2 (0) = 0, G 3 (0) = 0, G 4 (0) = 0.

В уравнения (46), (50) входят функции Fp(x), F(x), которые определяются формулами (12), (33). В свою очередь, в (12), (33) входят интегралы (15), (16), (36), (37), которые также можно путем дифференцирования по переменному пределу x свести к дифференциальным уравнениям. С учетом закона Снеллиуса [Кравцов, Орлов, 1980] имеем dPip — sin Pp d£0 Rip (x) dx     e 0   dzc dP2p _ sin Pp d£0 R2p (x)

------ — —----::--- dx e2   dzc dPi — sin Pn d£0 Ri (x)

dx     £0   dzc dP2 = sin Pn de0 R2 (x)

dx e0   dzc

Соответствующие начальные условия для (53)– (56) имеют вид P1p(xp)=0, P2p(0)=0, P1(0)=0, P2(xк)=0. Наконец, фундаментальные решения R1(x), R2(x), R1p(x), R2p(x), входящие в (13)–(16), (34)–(37), можно определить, интегрируя системы уравнений, полученные путем поочередного дифференцирования лучевых уравнений (17) по параметрам βn и βp, dR1 dx dR2 dx

ε Q dQ

-^y²-,   - — WR 1

sin² β_n dx

ε Q dQ

⁰7 ,    2- — WR 2

sin β_n dx

где

', = - ^0 Qip   dQip dx     sin2 β dx

p dR ε Q dQ

2p          0 2p        2p dx      sin2 β    dx

p

W =

d a z о

-А /с d\ ъ0

Л

к

Q i = ah *), ^d P n

Q 2 А * к - * ), Q ip =| в ° ( * ), Q 2p =Ц° ( * p — * ).

^d P n                  a P p             a ^ep

Начальные условия для (57), (58) имеют вид R 1 (0)=0, Q 1 (0)=1, R 2 ( x к )=0, Q 2 ( x к )=1, R 1p ( x p )=0, Q 1p ( x p )=1, R 2p (0)=0, Q 2p (0)=1.

Группируя уравнения (17), (45)–(58) для основного и пробного источников, имеем две независимые системы дифференциальных уравнений для расчета интегральных коэффициентов на заданной и вспомогательной трассах.

РЕЗУЛЬТАТЫ ЧИСЛЕННЫХ ЭКСПЕРИМЕНТОВ

Апробация методики прямой диагностики стохастического ионосферного канала была выполнена путем постановки численных экспериментов. Для оценок ожидаемых дисперсий траекторных характе-

ристик на заданных односкачковых трассах в каче-

стве входных данных использовались результаты расчетов траекторных моментов пробного сигнала на вспомогательной трассе, полученные при известных параметрах ионосферных неоднородностей. Ключевым вопросом в реализации предложенной методики является правильный выбор вспомогательной трассы для расчета характеристик сигнала на основной трассе. Как уже было сказано выше, пункт излучения пробного сигнала должен нахо-

слоев E и F2 соответственно. Параметры модели: z _mE= 150 км, z _m=320 км, у _mE=35 км, у _m= 120 км, f _крЕ=4 МГц, f _кр=8 МГц. Рабочая частота f =15 МГц. Траектории рассчитаны в секторе углов входа в канал 60°–80° с шагом 0.3°. Из рис. 2 видно, что, например, для основной трассы х к =1600 км (мода F2), подобными можно назвать трассы в интервале x p =1500–2000 км (мода F2), условно проходящие в той же области ионосферы, что и главная трасса. Между тем, подобными заданной трассе х _к= 1600 км не являются трассы в интервале x p =1500–2000 км, на которых происходит смена моды распространения (мода E). Также подобными заданной не являются трассы, проходящие через главный максимум ионизации слоя F2 и выходящие из ионосферы.

Для апробации методики диагностики рассматривались две трассы основного источника х к = 1600 км и х _к=1800 км (мода F2). В качестве вспомогательной была выбрана трасса, протяженностью x p =1700 км (мода F2).

Были взяты следующие параметры корреляционного эллипсоида с обобщенными свойствами поля случайных неоднородностей на вспомогательной трассе: μ²=0.0004 (соответствует возмущению электронной концентрации 2 % от фоновой ионосферы), a =10 км, V =100 м/с. Для выбранных параметров на основе (20)–(22) были рассчитаны дисперсии траекторных характеристик пробного сигнала на рабочей частоте f =15 МГц. Полученные значения составили c 2_p = (90)² (среднеквадратичное отклонение

фазового пути о = ^ = 286 м), ^ = 0.04 Гц^{2 ф}    2п f              f ^p

диться на некотором расстоянии от пункта приема основного сигнала, а пункт приема встречного пробного сигнала совпадает с пунктом излучения основного сигнала. Общие представления о возможных пробных трассах для оценки статистических характеристик сигнала на основной трассе в типичной ионосфере можно получить с помощью моделирования регулярной траекторной картины на основе уравнений (17). Анализ выполненных расчетов показал, что в зависимости от вида среднего профиля диэлектрической проницаемости ионосферы для заданной наклонной трассы можно найти ряд подобных трасс. В качестве примера на рис. 2 приведены траектории декаметрового сигнала в двухслойной ионосфере, заданной аналитической моделью

(о f p =0.2 Гц), О д , p = 2.04 мкс² (среднеквадратичное отклонение группового пути σ Δ L p = c σ Δ t p =428 м). Найденные величины дисперсий использовались в (38)–(40) для определения ожидаемых статистических характеристик сигналов на трассах основного источника. Интегральные коэффициенты, входящие в (38)–(40), рассчитывались путем совместного численного интегрирования систем уравнений для основного источника ((17), (49)–(52), (55)–(57)) и для пробного ((17), (45)–(48), (53), (54), (58)) с соответствующими начальными условиями. Полученные значения статистических характеристик приведены в табл. 1.

Таблица 1

Результаты пересчета статистических траекторных характеристик пробного сигнала в характеристики передаваемых сигналов ( x _p= 1700 км, f = 15 МГц)

х к , км	σ Φ , м	σ f , Гц	σ Δ L , м
1600	296	0.21	593
1800	281	0.19	652

f ²

^e0⁽ z 0 ) = ^{1 -} -p-ET exp

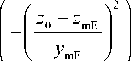
f ²

кp f2 p

-

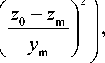
где z mE , z m , y mE , y m , f крЕ , f кр — высоты максимумов ионизации, полутолщины и критические частоты

Также был рассмотрен случай, когда трассы основного источника составляли x к =1600 км и x _к= 1700 км, а дальность вспомогательной трассы х _р=1800 км. Параметры корреляционного эллипсоида неоднородностей на вспомогательной трассе были взяты: μ²=0.0001 (возмущение электронной, концентрации 1 % от фоновой ионосферы), а =20 км V = 150 м/с. Дисперсии траекторных характеристик пробного сигнала в результате расчетов на основе

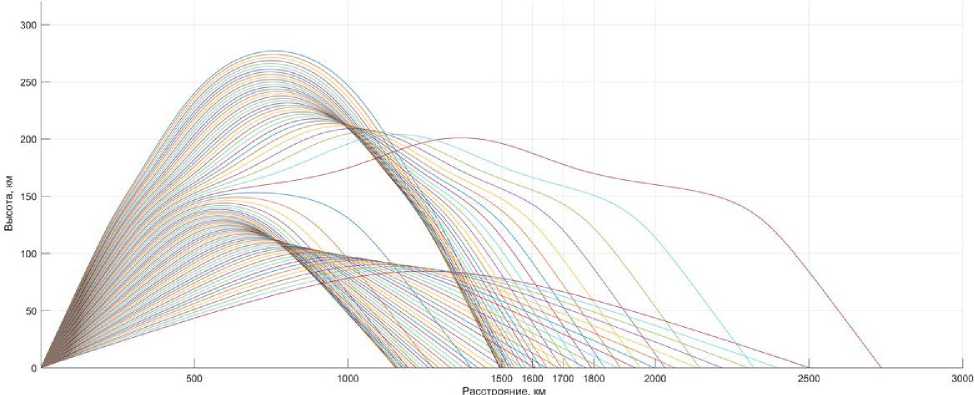
Рис. 2. Типичная лучевая картина в двухслойной ионосфере

(20)-(22) составили: о ф_р = (64)² (о_фр=203 м), o f = 0.0121 Гц² (о fp =0.11 Гц), о ² t p = 1.02 мкс² (σ_{Δ L p}=303 м). Статистические моменты пробного сигнала и рассчитанные интегральные коэффициенты (26)–(29), (41)–(44) использовались в (38)–(40) для определения дисперсий траекторных характеристик сигналов на заданных трассах. Результаты расчетов представлены в табл. 2.

Таблица 2

Статистические траекторные характеристики сигналов на заданных односкачковых трассах ( x _p= 1800 км, f = 15 МГц)

х к , км	σ Φ , м	σ f , Гц	σ Δ L , м
1600	214	0.13	332
1700	206	0.12	221

Из табл. 1, 2 следует, что рассчитанные ожидаемые флуктуации фазы, доплеровского смещения частоты и групповой задержки сигналов на односкачковых трассах находятся в соответствии с известными физическими представлениями о процессе рассеяния декаметровых радиоволн на ионосферных неоднородностях, превышающих размер первой зоны Френеля [Рытов и др., 1978]. Вместе с тем, при расположении пункта приема основного сигнала или пункта излучения пробного сигнала в окрестностях точек фокусировки поля основного источника полученные выше соотношения требуют модификации. В этих точках фундаментальные решения z0 , z0 обра щаются в нуль [Кравцов, Орлов, 1980], и в формулах (13), (14), (34), (35) возникают особенности, связанные с ветвлением решений краевых траекторных задач для основного и пробного источников.

ЗАКЛЮЧЕНИЕ

Предложена методика прямой диагностики статистических траекторных характеристик декаметро-вого сигнала на трассе наклонного зондирования ионосферы по данным измерений характеристик пробного сигнала, принятого в пункте излучения основного сигнала. При реализации методики используется модель средней диэлектрической проницаемости ионосферы. Такая модель может быть задана аналитическим профилем, наиболее соответствующим геофизической обстановке. Также допускается использование современных глобальных моделей, которые определяют электронную концентрацию ионосферы в виде дискретных данных. Применяя бикубическую сплайн-интерполяцию дискретных профилей электронной концентрации, можно обеспечить непрерывность производных первого и второго порядка, что требуется при расчетах. Результаты поставленных численных экспериментов показали работоспособность используемого математического аппарата для оценки ожидаемых вторых статистических моментов фазы, групповой задержки и доплеровского сдвига частоты декаметрового сигнала на односкачковых трассах средней протяженности в условиях, когда наземные пункты излучения и приема основного и пробного сигналов находятся вне окрестностей точек фокусировки волнового поля. Предложенная методика прямой диагностики стохастического радиоканала может быть использована в многочастотном режиме, исключая окрестность максимально применимой частоты. Для повышения качества диагностики возможно введение модели анизотропного корреляционного эллипсоида неоднородностей, ориентированного относительно радиотрассы. Параметры этого эллипсоида можно определить по характеристикам пробного сигнала на вспомогательной трассе с учетом априорной информации о типичных свойствах неоднородностей (например, их вытянутости вдоль силовых линий геомагнитного поля).