Диагональные контракции унитарных алгебр малой размерности

Основной сложностью создания квантовых компьютеров является быстрая декогеренция квантовых состояний открытых систем [1-3]. Диссипативные процессы в открытых квантовых системах с точки зрения контракций анализируются в работах [4-7]. Возможность сохранения когерентности открытых систем, по-видимому, демонстрирует нам природа на примере явлений фотосинтеза [8-11]. В данной работе мы приводим пример эволюции кубита, взаимодействующего с открытой системой, но сохраняющего когерентность. Все коммутаторы алгебры наблюдаемых при этом обнуляются, демонстрируя классическое поведение.

Известно, что диссипативная эволюция матрицы плотности кубита

I / J - в — гу А ~ 2 \ ^х + iy 1 — 5 )

описывается уравнением Линдблада [1,2,5]

+е6'^~5№^}У <2>

к                                '

или для наблюдаемых оу

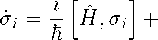
।                                                              (3)

к                                     '

Двухуровневая система в тепловом поле

Квантовая двухуровневая система [1] характеризуется наблюдаемыми ст_Ж1ст_У1ст_г с коммутационными соотношениями

[<7Ж, <7у] = 2/07,   [<7у,<7г] = 2г<тж,

[07, с®] = 2г<Ту, (4) образующими алгебру sm(2).

Рассмотрим двухуровневую систему в тепловом поле [6,12]. Обозначим оператор перехода из основного состояния |0) в возбужденное |1) как Л+ = <7+ = 11)(0|, а оператор перехода из верхнего состояния в основное — через Л = <т_ = |0) (11.

Пусть уравнение Линдблада содержит только диссипативную часть (Я = 0, У = Л), тогда вместо (2) имеем

|(п+ 1)(2<т_д<т+ - {<7+<т_,д}) +

7гг /                           \

+ -у ^2<т_+/э<т_ -     <т₊, р} j , (5)

где

Е .              1

2           ехр(^)-1

Здесь Ншо - разность уровней энергии основного и возбужденного состояний, 7 - константа взаимодействия, Т -температура окружающей среды.

Переписывая уравнение (5) в терминах переменных ж, у, z, получаем систему уравнений

.       / 1\ ж = —7 I п I ж,

. 2 = -7(1 + (2«+ аа^

решения которой имеют вид

' ж(Г) = е^^Ко,

( y(t) = е-^Ео,

Ак = е"⁷^²^⁴ L + —

.                     \     1 + 2гг/

где z_s = — (1 + 2n)^-1. С учетом (6), имеем z_s = — 1 при нулевой температуре Т = 0 окружающей среды, что соответствует основному состоянию системы |0) с матрицей плотности р = |0) (0| = ^ q 1 ^ • При возрастании температуры Т —i оо получаем z_s -а

0, что соответствует полностью смешанному состоянию системы р = |(|0>(0| + 11)(1|) = I ^ q ^ ^ •

Формулы (8) при Г —i оо описывают эволюцию кубита. Поскольку в процессе эволюции ж и у —i 0, то матрица плотности (1) диагонализируется, что соответствует потере кубитом когерентности. Траектории эволюции кубита изображены на рис.1.

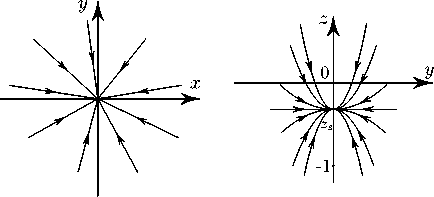
Рис. 1. Траектории эволюции кубита (8) в плоскостях (ж, у) и (y,z).

Fig. 1. Evolution trajectories of a qubit (8) in the planes (x,y) and (y,z).

Что касается наблюдаемых системы, то уравнение (3) перепишется

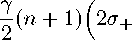
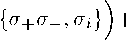
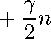
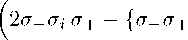
Для наблюдаемых ст_ж, ст_у, а_г оно принимает вид

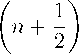
А 7 I + 2 ) ’

<7% = —7I — 7(2п + 1)<тг и имеет решения оАА = е”7^)4^, стуА = e-^+^tTy,                   (11)

= е-7(1+2пЕ<т3 + ——

V              V 1 + 2пУ 1 + 2п с коммутационными соотношениями

• <7 1 — 2г Г<т Ч- с-'⁷²" ^{1 1}

[<7у, <7z]t = 2ге-7<<7ж,   [<7Z, сгж]4 = 2ге-74сгу. (12)

Переобозначая <7₃ —><73 + ₁₊^z_2n в пределе t —> оо имеем алгебру Гейзенберга.

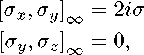
Таким образом, в результате теплового взаимодействия кубита с окружающей средой первоначально некоммутирующие квантовые наблюдаемые 07,07,07 (4) в процессе эволюции частично приобретают классические черты, что проявляется в изменении (контракции) их коммутационных соотношений до алгебры Гейзенберга.

Двухуровневая система в тепловом и электромагнитном полях

Добавим теперь в правую часть уравнения (5) гамильтониан взаимодействия с когерентным электромагнитным полем

Hj = hvx.(14)

Уравнение Линдблада (2) преобразуется в систему уравнений

./ 1\ ж = —7 I п + — I ж,

• < .         ((15)

y=-7l«+-ly - Zhz, z = -7(1 + (2п + 1)г) + 2/гу.

Эта система имеет предельную точку типа узел с координатами ж8 = 0,

4/17

2/8 = 72(2n + I)2 + 8/г2 ’           (16)

_      7²(2п + 1)

⁸ ^(Zn + I)² + 8/г²

Решения системы (15) описываются формулами

ж(/) = e-7(n+^Ko,

?/(i) = (//о - y_s) (Сфе^-* - С_е^-Х+^ +

+  .                        _ e-A+t) + у 72 (п + |)2 — 167г2

z(t) = (г₀ - z_s) (С^е^-^⁴ - С_е^-Х-^ +

+2/г(уо ^— Уз) (е ^X+t — е 4- %₈₁    (17)

где

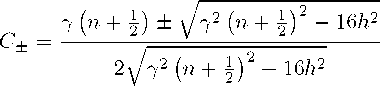
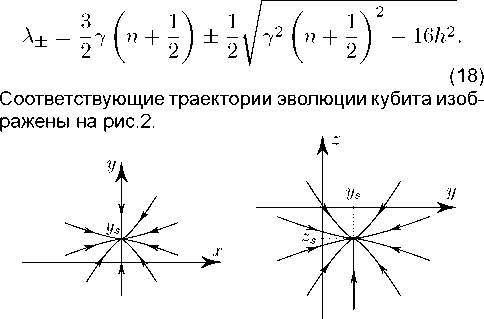
Рис. 2. Траектории эволюции кубита (15) в плоскостях (ж, у) и (у, z).

Fig.2. Evolution trajectories of a qubit (15) in the planes (т,у) and (y,z).

Уравнения для наблюдаемых в этом случае имеют вид

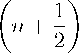
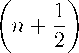
о у — 2ао4,

dz = —7(1 + (2n + 1)04) + 2acry, а решения даются выражениями тх^ = е"^п^КЖ1

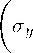
72(2и + I)2 + 8/г2 , х (Сфе^-* - С_е"х+^ + у 72 (п+ |)2 — 16/г2

72(2п+1) Л f.

72(2п+1)2 + 8/г2 Р

7²(2п + I)² + 8/г²

/ \ А         72(2п +1)\

Х х (С+е-А+‘-С_е-А-‘) +

/            4/г7\

+2/г I <ту     —— • —у •    „ 1 I х

\     72(2гг + I)2 + 8/г2 / х (e-x+t - е-^^ -

7²(2п + 1)

--—----------1.           (20) 7²(2п + I)² + 8/г²

В пределе t ^ оо алгебра наблюдаемых становится абелевой

[^^yloc = [^yj^zloc = ^,<7^^ = 0.    (21)

Таким образом, в результате теплового и электромагнитного взаимодействия двухуровневой квантовой системы с окружающей средой первоначально некоммутирующие квантовые наблюдаемые <т_ж, (7_y,a_z (4) в процессе эволюции теряют квантовые свойства и становятся чисто классическими коммутирующими наблюдаемыми. Однако система при этом сохраняет свойство когерентности.