Диаграмма состояния системы CaO-MgO-MnO

Автор: Макровец Лариса Александровна, Самойлова Ольга Владимировна

Журнал: Вестник Южно-Уральского государственного университета. Серия: Металлургия @vestnik-susu-metallurgy

Рубрика: Физическая химия и физика металлургических систем

Статья в выпуске: 1 т.21, 2021 года.

Бесплатный доступ

Построение диаграмм состояния многокомпонентных систем является одной из фундаментальных задач не только в области материаловедения, но и для металлургических технологий. Термодинамическое моделирование при этом является одним из базовых инструментов исследователя, особенно при ограниченном количестве достоверных литературных экспериментальных данных или при значительных сложностях, сопровождающих постановку эксперимента. Термодинамический расчет обычно основывается на таких физико-химических данных, как изменение энергии Гиббса при осуществлении фазовых переходов, термодинамических характеристиках составляющих исследуемую систему веществ и значениях активностей компонентов равновесных фаз (расплава, твердых растворов и т. д.). В настоящей работе было проведено термодинамическое моделирование диаграмм состояния систем MgO-CaO, MnO-CaO и CaO-MgO-MnO. Для определения активностей компонентов оксидного расплава в указанных выше системах использовалась теория субрегулярных ионных растворов. Активности компонентов твердых растворов в системах MgO-CaO и MnO-CaO определялись с использованием теории регулярных ионных растворов, а в системе CaO-MgO-MnO - с использованием теории субрегулярных ионных растворов. В ходе расчетов были уточнены границы фазовых равновесий и положения линий ликвидус и солидус в двойных оксидных системах, а также координаты проекции поверхности ликвидус в исследуемой тройной оксидной системе. Показано, что при значительных концентрациях оксида марганца в системе CaO-MgO-MnO два твердых раствора (на основе оксида магния и на основе оксида кальция) объединяются в один твердый раствор |CaO, MgO, MnO|тв.р. Полученные результаты согласуются с немногочисленными экспериментальными данными по исследуемым системам.

Еще

Термодинамическое моделирование, фазовые равновесия, теория субрегулярных ионных растворов, система CaO–MgO–MnO, диаграмма состояния

Короткий адрес: https://sciup.org/147233976

IDR: 147233976 | DOI: 10.14529/met210101

Текст научной статьи Диаграмма состояния системы CaO-MgO-MnO

Диаграммы состояния систем – фундаментальная основа металлургических технологий. Так диаграммы состояния оксидных систем позволяют определять свойства шлаковых систем, например, зависимость температуры плавления от состава, что является ключевым моментом при прогнозировании оптимальных композиций шлака для того или иного этапа металлургического процесса.

Система CaO–MgO–MnO является одной из основных при рассмотрении шлаков сталеплавильного производства. Информация, представленная в литературе [1–3] о виде данной диаграммы состояния, несколько ограничена и не дает представления о полной проекции поверхности ликвидус. В справоч-

нике [1] обобщены данные по исследованию E. Woermann и A. Muan [2], где приведено только одно изотермическое сечение при 1500 °С для давления в 10–9 атм, и данные по работе H. Schenck и др. [3], где фазовая диаграмма CaO–MgO–MnO приведена в виде схематически представленных изотермических разрезов для температур 2000, 2200 и 2400 °С.

С другой стороны, моделирование – универсальный инструмент для прогнозирования хода технологических процессов. Как известно, можно производить расчет не только технологических параметров, но и реализующихся в ходе металлургического производства фазовых равновесий в металлических и шлаковых системах [4].

Цель настоящей работы – термодинамическое моделирование диаграмм состояния двойных и тройной оксидных систем, принадлежащих к системе CaO–MgO–MnO. В данном исследовании рассмотрены диаграммы состояния систем MgO–CaO, MnO–CaO и CaO–MgO–MnO. Ранее нами была построена диаграмма состояния системы MnO–MgO [5], которая представляет собой систему с неограниченной растворимостью компонентов как в жидком, так и в твердом состоянии.

Для моделирования линий ликвидус двойных оксидных систем MgO–CaO и MnO–CaO в данной работе использовали теорию субрегулярных ионных растворов [4]. Активности компонентов в оксидном расплаве для двойной оксидной системы могут быть рассчитаны по фор- мулам:

1g о , = 1g x , +

³ x i ^X 2 Q iii2 ⁺ x i ^X 2 ( ^{2 3} x i ) Q ii22 ⁺ ^X 2 ( 1 ³ x i ) Q i222 .

2,3026 RT

1g a 2 = 1g X 2 +

xi (i 3X2 )Qiii2 + xi X2 (2 3X2 )Qii22 + 3xi X2Qi222 2,3026RT где xi – ионные доли катионов компонентов оксидного расплава; Qijkl – энергетические параметры теории, Дж/моль; R – универсальная газовая постоянная, R = 8,314 Дж/(моль·К); Т – температура, К.

Для моделирования поверхности ликвидус тройной оксидной системы CaO–MgO–MnO также использовали теорию субрегулярных ионных растворов [4]. Активности компонентов в оксидном расплаве тройной оксидной системы могут быть рассчитаны по формулам:

^Xi ⁽ ^{i 3} ^X 2 ) Q iii2 ⁺ x i ^X 2 ⁽ ^{2 3} ^X 2 ) Q ii22 ⁺

1g a ₂ = v₂1g x₂ + v₂

⁺ ³ x i ^X 2 ⁽ ⁱ - ^X 2 ) Q i222 - ³ ^X 3 ^X 3 Q iii3 -

-3 X i² X 2 (2-3 X i ) Q ii33 -3 X i X 3Q333 +

+ ³ ^X 2 ^X 3 ⁽ⁱ ^- ^X 2 ) Q 2223 ⁺ ^X 2 ^X 3 ⁽ ² ^- ³ ^X 2 ) ^Q 2233 ⁺+ X 3³ (i - 3 X 2 ) Q 2333 + X 2 X 3 (i - 3 X 2 ) Q ii23 + _⁺ ^X i ^X 2 ^X 3 ⁽² ^- ³ ^X 2 ) Q i223 ⁺ ^X i ^X 3 ⁽ⁱ ^- ³ ^X 2 ) Q i233 .

/2,3026 RT ;

	³ x i ^X 2 Q iii2 ⁺ x i ^X 2 ⁽ ^{2 3} x i ) Q ii22 ⁺ ^X 2 ⁽ ^{i 3} x i ) Q i222 ⁺
	+3 X i² x 3 (i - X i ) Q iii3 + X i x 3² (2 - 3 x ) Q hjj +
1g a i = v , 1g X i + V i	⁺ ^X 3 ⁽ ⁱ - ³ x i ) Q i333 - ³ ^X 2 ^X 3⁽ⁱ - x i ) Q 2223 - ³ ^X 2 ^X 3 Q 2233 - ^— ³ x 2 x 3 ⁽ⁱ ^- 3 ^X i ) Q 2333 ⁺ x i ^X 2 ^X 3 ⁽² ^- ³ x i ) Q ii23 ⁺	/2,3026 RT ;	(3)
	⁺ ^X 2 ^X 3 ⁽ⁱ - ³ x i ) Q i223 ⁺ ^X 2 ^X 3 ⁽ⁱ - ³ x i ) Q i233

	³ ^X i3 ^X 2 Q iii2 ³ ^X i2 ^X 2 Q ii22 ³ ^X i ^X 2 Q i222 ⁺
	+ X 3 (i - 3 X 3 ) Q iii3 + x i² x 3 (2 - 3 X 3 ) Q_n 33 +
1g a 3 = V 3 1g x 3 + V 3	⁺ ³ ^X i ^X 3 ⁽ ⁱ ^- ^X 3 ) ^Q i333 + x 2 ⁽ⁱ ^- ³ x 3 ) ^Q 2223 ⁺ ⁺ ^X 2 ^X 3 ⁽² ^- ³ ^X 3 ) Q 2233 ⁺ ³ ^X 2 ^X 3 ⁽ⁱ ^- ^X i ) Q 2333 ⁺ ⁺ ^X i ^X 2 ⁽ⁱ ^- ³ ^X 3 ) ^Q ii23 ⁺ ^X i ^X 2 ^X 3 ⁽² ^- ³ ^X 2 ) ^Q i223 ⁺	/2,3026 RT .	(5)
	_+ X i X 3² (i - 3 X 2 ) Q i233 .

Для моделирования линий солидус в двойных оксидных системах MgO–CaO и MnO–CaO использовали теорию регулярных ионных растворов [4], активности компонентов в твердом растворе могут быть рассчитаны по формулам:

1g ti l = 1g X 1 +

x 2² Q 12 ;

2,3026 RT

1g ti 2 = 1g X 2 +

x 1² Q 12

2,3026 RT ,

где Q ₁₂ – энергетический параметр теории, Дж/моль.

Для проведения расчетов необходимы были данные по температурам и энтальпиям плавления оксидов кальция, магния и марганца: 2613 [6], 2825 [7], 1875 °С [7] и 52 300 [3], 77 400 [7], 54 395 [8] Дж/моль соответственно.

Диаграмма состояния системы MgO–CaO изучалась в работах [9–14]. В работе 1916 года авторами G.A. Rankin и H.E. Merwin [9] диаграмма состояния системы MgO–CaO представлена как диаграмма с простой эвтектикой, без твердых растворов. В работе M.Yu. Lavrentiev и др. [10] области твердых растворов на основе оксида магния или оксида кальция практически не различимы и взаимная растворимость оксидов не превышает 1 ат. %. В расчетных работах [11–13] растворимость MgO в CaO колеблется от 15 до 20 ат. %, а CaO в MgO от 5 до 10 ат. %. В работе же R.C. Doman и др. [14] приводятся экспериментальные данные и построена диаграмма состояния системы; при моделировании мы опирались прежде всего именно на эти экспериментальные данные.

В монографии [4] подробно описана методика моделирования диаграмм состояния оксидных систем с соединением (на примере системы FeO–Al2O3) и диаграмм состояния оксидных систем c расслоением (на примере системы FeO–SiO2). Методика же расчета диаграмм состояния оксидных систем, в которых присутствуют твердые растворы с ограниченной растворимостью (таких как система MgO–CaO), отличается, поэтому кратко остановимся на ней.

Согласно формулам (1), (2), (6), (7) необходимо было определить три энергетических параметра Q_ijkl для оксидного расплава и по одному энергетическому параметру для двух твердых растворов (для раствора CaO в MgO – Q 12 , для раствора MgO в CaO – Q 22 ). Энергетические параметры используемых теорий для расчета диаграммы состояния системы MgO–CaO определяли по характерным точкам диаграммы (из литературных данных). Для оксидного расплава в качестве характерной точки рассматривалась точка эвтектики. Для твердых растворов в качестве характерных точек выступали точки предельной концентрации в твердых растворах.

Следует отметить, что при расчете возникла необходимость рассмотрения дополнительных точек на линиях ликвидус и солидус для приведения в соответствие количества уравнений и количества неизвестных. Для этой же цели при моделировании в качестве неизвестного была выбрана энтальпия плавления оксида CaO, которая заранее известна (52 300 Дж/моль [3]), и при дальнейшем расчете мы находили ее с точностью до 0,001 Дж/моль.

Таким образом, при моделировании были рассмотрены следующие фазовые равновесия (рис. 1):

1) кристаллизация из оксидного расплава твердого раствора оксидов |MgO, CaO| тв.р. на основе MgO, входящего в эвтектику I (точки I и II);
2) кристаллизация из оксидного расплава твердого раствора оксидов |MgO, CaO| тв.р. на основе CaO, входящего в эвтектику I (точки I и III);
3) кристаллизация из оксидного расплава твердого раствора оксидов |MgO, CaO| тв.р. на основе MgO (точки IV и V).

При проведении расчетов диаграммы использовали следующие данные (см. рис. 1):

– координаты точки эвтектики (точка I):

tI = 2370 °С (TI = 2643 К); (MgO)I = 33,0 мас. %; (CaO)I = 67,0 мас. % или x1I = 0,4066; x2I = 0,5934;

– координаты точки II:

tII = 2370 °С (TII = 2643 К); (MgO)II = 92,2 мас. %; (CaO)II = 7,8 мас. % или x1II = 0,9427; x2II = 0,0573;

– координаты точки III:

tIII = 2370 °С (TIII = 2643 К); (MgO)III = 17,0 мас. %; (CaO)III = 83,0 мас. % или x1III = 0,2218; x2III= 0,7782;

– координаты точки IV:

tIV = 2600 °C (TIV = 2873 К); (MgO)IV = 55,5 мас. %; (CaO)IV = 44,5 мас. % или x1IV = 0,6344; x2IV = 0,3656;

– координаты точки V:

tV = 2600 °C (TV = 2873 К); (MgO)V = 94,71 мас. %; (CaO)V = 5,29 мас. % или x1V = 0,9634; x2V = 0,0366.

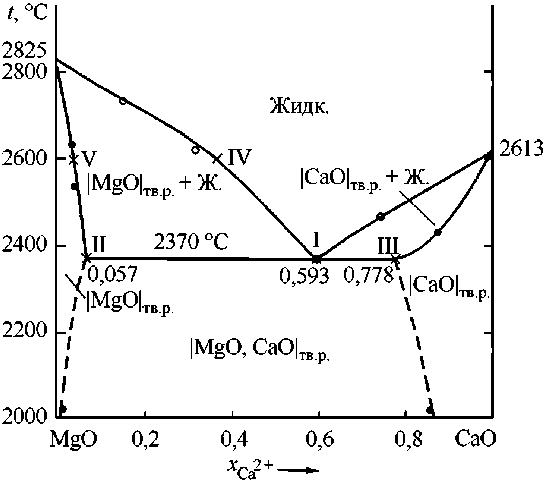
Рис. 1. Диаграмма состояния системы MgO–CaO:

, , Χ – расчет; ○, • – экспериментальные данные R.C. Doman и др. [14]

При составлении системы уравнений совместно использовали уравнения (1) и (6) для оксидного расплава и твердого раствора на основе оксида магния MgO или (2) и (7) для оксидного расплава и твердого раствора на основе оксида кальция CaO. Для каждого из трех рассматриваемых равновесий записывали по два уравнения. Следовательно, для определения энергетических параметров используемых теорий необходимо было решить систему из шести уравнений:

2,3026 RT 1 1g x I + 3 ( x I ) 2 ( x 2 ) 2 Q_m 2 + x I ( x 2 ) 2 ( 2 - 3 x I ) Q_U22 + ( x 2 ) 3 ( 1 - 3 x I ) Q i ₂₂₂ -

-2,3026RT111g x” -(x 2I )2 Q12 = —A mH;. (MgO)+ T’ A mH° (MgO);(8)

Tm Tm (MgO)

2,3026 RT 1 1g x 2 + ( x ? ) 3 ( 1 - 3 x 2 ) Q _ni2 + ( x ? ) 2 x 2 ( 2 - 3 x 2 ) Q 1122 + 3 ( x l ) 2 ( x 2 ) 2 Q 1222 -

-2,3026RT111g x ” -(x” )2 Q12 = -A mH;„ (CaO)+ TI A mH° (CaO);(9)

Tm Tm (CaO)

2,3026 RT 1 1g x I + 3 ( x I ) 2 ( x 2 ) 2 Q 1112 + x I ( x 2 ) 2 ( 2 - 3 x I ) Q_U22 + ( x 2 ) 3 ( 1 - 3 x I ) Q 1222 -

-2,3026RT1111g x|II -(x 2II )2 Q 22 = -A mH;. (MgO)+ T’ A mH° (MgO);(10)

Tm Tm (MgO)

2,3026 RT 1 1g x 2 + ( x ? ) 3 ( 1 - 3 x 2 ) Q 1112 + ( x ? ) 2 x 2 ( 2 - 3 x 2 ) Q_m 2 + 3 ( x ? ) 2 ( x 2 ) 2 Q 1222 -

-2,3026RT1111g x 211 - (< )2 Q22 = -A mH° (CaO) + TI A mH° (CaO);(11)

x Tm Tm (CaO)

IV IV IV IV IV IVIV

^2,3026 RT lg x i + ³ ( x i ) ( x 2 ) Q 1112 + ^X 1 ( ^x 2 ) ( ² - ³ ^X 1 ) Q 1122 +

+ ( x 2V ) ³ ( 1 - 3 X 1IV ) Q 1222 - 2,3 0 26 RT ^V lg X V - ( x 2V ) ² Q 12 =

=-AmH;. (MgO) + AmH-r (MgO);(12)

Tm Tm (MgO)

IV IV IV 3 IV IV 2 IVIV

^2,3026 RT ^lg x 2 + ( x i ) ( ^{1 3} x 2 ) Q 1112 ⁺( ^X1 ) ^x 2 ( ^{2 3} ^x 2 ) Q 1122 ⁺

+ 3 ( x |^V ) ² ( X 2V ) ² Q 1222 - 2,3 026 RT ^V lg X V - ( x V ) ² Q 12 =

=-ЛmH.. (CaO) + —— ЛmH.. (CaO).(13)

Tm Tm (CaO)

Согласно расчетам были получены следующие значения (Дж/моль): Q 1112 = 34 913; Q 1122 = = 23 919; Q 1222 = 31 326; Q 12 = 67 425; Q 22 = 52 869; A _mH⁰ ( CaO ) = 52 300.

Используя полученные значения энергетических параметров, рассчитали диаграмму состояния системы MgO–CaO (см. рис. 1). Проведенный нами расчет по теории субрегулярных ионных растворов (для оксидного расплава) и теории регулярных ионных растворов (для твердых растворов оксидов) согласуется с экспериментальными данными работы [14].

Диаграмма состояния системы MnO–CaO изучалась в работах [3, 15]. Данная диаграмма представляет собой линзу с неограниченной растворимостью компонентов, как в жидком, так и в твердом состоянии. В работе K.R. Poeppelmeier и др. [15] исследовалась только низкотемпературная часть диаграммы, а в работе авторов H. Schenck и др. [3] – только высокотемпературная (выше 1750 °С) часть диаграммы.

Активности компонентов оксидного расплава и твердого раствора в системе MnO–CaO также рассчитывали по формулам (1), (2), (6), (7). Для оксидного расплава получили энергетические параметры теории (Дж/моль): Q ₁₁₁₂ = +15 535; Q ₁₁₂₂ = +708; Q ₁₂₂₂ =+6993. Для твердого раствора оксидов энергетический параметр оказался равен Q 12 = +7765 Дж/моль.

На рис. 2 приведена диаграмма состояния системы MnO–CaO, рассчитанная в данной работе, и экспериментальные данные работы [3]. Видно, что расчетная линия хорошо согласуется с экспериментальными данными.

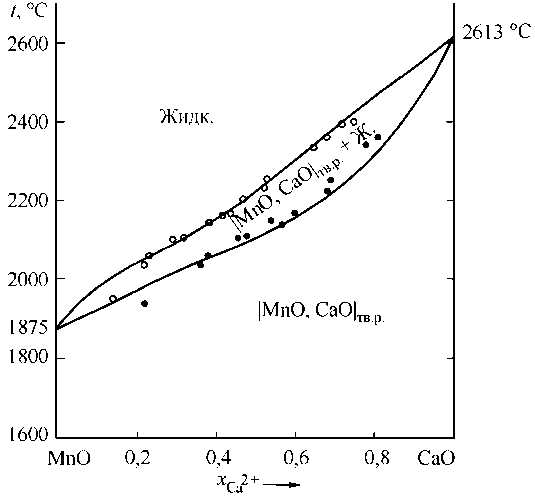
Рис. 2. Диаграмма состояния системы MnO–CaO:

– расчет, ○, • – экспериментальные данные H. Schenck и др. [3]

Энергетические параметры Q ijkl теории субрегулярных ионных растворов для расчета твердых растворов на основе CaO или MgO и оксидного расплава (CaO, MgO, MnO)

Система	Q ijkl , Дж/моль
Твердый раствор на основе CaO
CaO–MgO	+52 869	+105 738	+52 869
CaO–MnO	+7765	+15 530	+7765
MgO–MnO	–43 919	–88 669	–43 919
CaO–MgO–MnO	+70 000	+200 000	–20 000
Твердый раствор на основе MgO
CaO–MgO	+67 425	+134 850	+67 425
CaO–MnO	+7765	+15530	+7765
MgO–MnO	–43 919	–88 669	–43 919
CaO–MgO–MnO	+106 461	+54 777	–4883
Оксидный расплав
CaO–MgO	+31 326	+23 919	+34 913
CaO–MnO	+6993	+708	+15 535
MgO–MnO	–25 072	–88 669	–35 635
CaO–MgO–MnO	+13 288	–16 725	–41 541

При рас че те д и а гр а ммы с ос тоян и я с и с темы CaO–MgO–MnO ак тив н ос ти к омп он е н тов о к с и д н о го р а с п ла ва и тве рд ых ра с тв ор ов о кси д ов ра сс чи тыв а ли п о т еори и с у б ре гу лярн ых и он н ых ра с тв оров . При ра сче те тр ой н ой о ксидной системы необходимо учи тыв а ть э н ерг е ти че ск и е п а р а ме тры , п од об ра н ные и д ля дв ойн ы х ок с ид н ых с и с т ем. В с е н е об ход и м ые для ра с че та д и а гр а ммы с ос тоян и я с и с те м ы CaO–MgO–MnO э н ерге т и че с к и е п а ра м е тр ы

теории субрегулярных ионных растворов приведены в таблице.

На рис. 3 приведена расчетная диаграмма состояния системы CaO–MgO–MnO в интервале температур от 1900 до 2800 °С с шагом в 100 градусов. На диаграмме имеются две обширные области твердых растворов (на основе CaO и на основе MgO), в каждом из которых растворяется оксид марганца. Линия a – b разделяет области фазовых равновесий с каж-

(1875) MnO

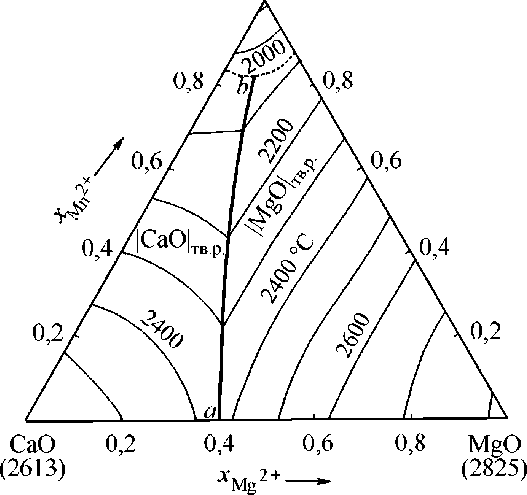
Рис. 3. Расчетная диаграмма состояния системы CaO–MgO–MnO

дым из этих твердых растворов на поверхности ликвидус и соответствует линии трехфазного равновесия «оксидный расплав – твердый раствор на основе оксида кальция – твердый раствор на основе оксида магния». Следует отметить, что при значительных концентрациях оксида марганца в системе два твердых раствора объединяются в один твердый раствор |CaO, MgO, MnO| тв.р , концентрационные границы которого обозначены на поверхности ликвидус штриховой линией. Такой расчет фазовых равновесий основывается на экспериментальных данных работы авторов H. Schenck и др. [3].

Согласно рис. 3 увеличение концентраций CaO и MgO приводит к значительному повышению температуры плавления всей системы CaO–MgO–MnO. Таким образом, для снижения температуры плавления подобной шлаковой системы необходимо введение дополнительных легкоплавких компонентов.

Выводы

Проведено термодинамическое моделирование диаграмм состояния оксидных сис-

тем MgO–CaO, MnO–CaO и CaO–MgO–MnO. Подобраны энергетические параметры теорий субрегулярных ионных растворов и регулярных ионных растворов, используемых при расчете. Определен алгоритм для термодинамического моделирования фазовых равновесий в диаграммах с ограниченной растворимостью компонентов (в твердых растворах). Полученные расчетные положения линий ликвидус и солидус, а также поверхности ликвидус согласуются с имеющимися в литературе данными по диаграммам состояния исследуемых систем. Согласно проведенному моделированию система CaO–MgO–MnO характеризуется достаточно высокими температурами плавления. Таким образом, для снижения температуры плавления подобной шлаковой системы необходимо введение дополнительных легкоплавких компонентов.

Работа выполнена при поддержке Правительства РФ (Постановление № 211 от 16.03.2013 г.), соглашение № 02.A03.21.0011.

Список литературы Диаграмма состояния системы CaO-MgO-MnO

Slag Atlas. 2nd Edition. Edited by Verein Deutscher Eisenhüttenleute (VDEh). – Düsseldorf: Verlag Stahleisen GmbH, 1995. – P. 133.
Woermann, E. Derivation of approximate activity-composition relations in MgO–MnO solid solutions / E. Woermann, A. Muan // Materials Research Bulletin. – 1970. – Vol. 5, no. 10. – P. 779–788. DOI: 10.1016/0025-5408(70)90092-9
Schenck, H. Das System MnO(–FeO)–MgO(–CaO) und seine Verteilungsgleichgewichte mit flüssigem Mangan und Eisen-Mangan-Legierungen / H. Schenck, M.G. Frohberg, R. Nünninghoff // Archiv Für Das Eisenhüttenwesen. – 1964. – Vol. 35, no. 4. – P. 269–277. DOI: 10.1002/srin.196402318
Михайлов, Г.Г. Термодинамика металлургических процессов и систем / Г.Г. Михайлов, Б.И. Леонович, Ю.С. Кузнецов. – М.: Издат. Дом МИСиС, 2009. – 520 с.
Михайлов, Г.Г. Термодинамическое моделирование диаграмм состояния двойных и тройных оксидных систем, принадлежащих к системе FeO–MgO–MnO–Al2O3 / Г.Г. Михайлов, Л.А. Макровец, О.В. Самойлова // Новые огнеупоры. – 2020. – № 6. – С. 47–50. DOI: 10.17073/1683-4518-2020-6-47-50
Wriedt, H.A. The Ca–O (Calcium–Oxygen) System / H.A. Wriedt // Bulletin of Alloy Phase Diagrams. – 1985. – Vol. 6, no. 4. – P. 337–342. DOI: 10.1007/BF02880517
Kubaschewski, O. Metallurgical Thermochemistry / O. Kubaschewski, C.B. Alcock. – Oxford: Pergamon Press Ltd Publ., 1979. – 392 p.
Wicks, C.E. Thermodynamic properties of 65 elements: their oxides, halides, carbides, and nitrides / C.E. Wicks, F.E. Block // U.S. Dep. of the Interior. Bureau of Mines. Bulletin. – 1963. – Vol. 605. – 146 p.
Rankin, G.A. The ternary system CaO–Al2O3–MgO / G.A. Rankin, H.E. Merwin // Journal of the American Chemical Society. – 1916. – Vol. 38, no. 3. – P. 568–588. DOI: 10.1021/ja02260a006
Ab Initio Calculation of Phase Diagrams of Oxides / M.Yu. Lavrentiev, N.L. Allan, G.D. Barrera, J.A. Purton // J. Phys. Chem. B. – 2001. – Vol. 105. – P. 3594–3599. DOI: 10.1021/jp004124
Hillert, M. Thermodynamic calculation of the CaO–MgO system / M. Hillert, W. Xizhen // Calphad. – 1989. – Vol. 13, no. 3. – P. 267–271. DOI: 10.1016/0364-5916(89)90006-0
Yin, Y. The phase diagrams and thermodynamics of the ZrO2–CaO–MgO and MgO–CaO systems / Y. Yin, B. Argent //Journal of Phase Equilibria. – 1993. – Vol. 14, no. 5. – P. 588–600. DOI: 10.1007/BF02669140
Zhang S. Effects of CaO and Al2O3 Added to MgO–C Refractories on MgO–C Reaction / S. Zhang, A. Yamaguchi // Journal of the Ceramic Society of Japan. – 1996. – Vol. 104, no. 2. – P. 84–88. DOI: 10.2109/jcersj.104.84
Phase Equilibria in the System CaO–MgO / R.C. Doman, J B. Barr, R.N. McNally, A.M. Alper // Journal of the American Ceramic Society. – 1963. – Vol. 46, no. 7. – P. 313–316. DOI: 10.1111/j.1151-2916.1963.tb11737.x
Poeppelmeier, K.R. Oxide solid solutions derived from homogeneous carbonate precursors: The CaO–MnO solid solution. / K.R. Poeppelmeier, H.S. Horowitz, J.M. Longo // Journal of the Less Common Metals. – 1986. – Vol. 116, no. 1. – P. 219–227. DOI: 10.1016/0022-5088(86)90231-6

Еще

Статья научная