Диаграммы-изохроны высокопрочного модифицированного бетона

Экспериментальные исследования по изучению свойств высокопрочных бетонов, модифицированных на органоминеральной основе, проведенные в последние годы Н. И. Карпенко, С. С. Каприеловым, И. М. Безгодовым, Е. Н. Кузнецовым, А. А. Андриановым, Д. С. Ромкиным и другими, подтвердили установленные ранее закономерности нелинейной ползучести бетона: инвариантность быстронатекающих деформаций относительно возраста бетона в момент за-гружения и противоречие принципу наложения воздействий. Эти обстоятельства создают существенные трудности при решении задач ползучести на базе общих нелинейных теорий, в частности двухкомпонентной модели [1]. Указанных противоречий при решении задач длительного деформирования можно избежать, если использовать так называемый диаграммный подход с представлением диаграмм деформирования бетона в виде диаграмм-изохрон.

Диаграммой-изохроной деформирования бетона называется кривая в координатах деформации-напряжения, все точки которой достигаются за равный промежуток времени – время нагружения. В общем случае при построении диаграмм-изохрон различают три условных ре-

жима нагружения: при действии постоянных напряжений, при линейном росте напряжений и при линейном росте деформаций. Поведение бетона при действии постоянных напряжений изучено наиболее полно, однако в реальных конструкциях такой режим практически не встречается. Второй режим существенно ближе к условиям реального нагружения, но сложен технически при проведении экспериментов. Последний режим нагружения, технически наиболее сложный, позволяет получить исчерпывающие данные о деформативных свойствах материала и выйти на нисходящую ветвь диаграммы деформирования.

Если длительность действия нагрузки не превышает одних суток, диаграммы-изохроны всех трех режимов практически совпадают с диаграммой кратковременного загружения. В дальнейшем, с увеличением времени нагружения, зависимость диаграммы-изохроны от режима изменения напряжений становится более существенной, однако после примерно 100 суток нагружения эта разница практически исчерпывается. Учитывая практическую направленность задачи, предлагаемые в настоящей работе зависимости предполагают постоянство дейст-

вующих напряжений в течение всего времени нагружения, при этом теоретически допускается возможность работы бетона на нисходящей ветви диаграммы.

Связь между напряжениями и относительными деформациями бетона, выраженная через коэффициент секущего модуля, в наиболее общем виде предложена Н. И. Карпенко [2]. Для диаграмм-изохрон эта зависимость приобретает вид

^ ( t , т ) =------------,

⁷   E_b ( t , т >_ь ( t - т )

где t – текущее время, τ – возраст бетона в момент загружения, ( t – τ ) – время нагружения.

Коэффициент секущего модуля определяется по формуле

b ^{( (} t ^{- T} ) = v ⁽ t^{, T} ) ± [ ^v 0 ^{- V} b ⁽ t , ^T ) ]7 ^{1 -} ® i⁽ t ^{, T} ) S ^{- ю} 2 ⁽ t ^{, T} ) n 2 , ⁽²⁾

где n = о _ь ( т ) / R_b ( t , т ) - уровень напряжений в момент времени t .

Знак «плюс» соответствует восходящей, а «минус» – нисходящей ветви диаграммы-изохроны. Кроме этого, требуется соблюдение очевидного равенства

® 1 (t , т ) + ст ₂( t , т ) = 1 .

Коэффициент секущего модуля в вершине диаграммы-изохроны vь(t,т) = Rb (t,т)/ Еь(t,т )еь о( t,т),          (3)

где £ _{ь 0} ( t , т ) - абсцисса вершины.

Ордината вершины диаграммы-изохроны определяется по эмпирической формуле, учитывающей экспериментально установленное снижение прочности бетона в условиях длительного нагружения

R b ⁽ t ^{, т} ) = [ k ^{+ (1 -} k ^{) ф (} t ^{- т} ) ] R b ^{( т} ) ,        (4)

где k – коэффициент, отражающий экспериментально установленные пределы снижения прочности бетона при длительном нагружении и изменяющийся от 0,9 до 0,75. При практическом проектировании рекомендуется принимать к = 0,85; Ф ( t - т ) - эмпирическая функция.

Анализ экспериментальных данных показал, что в диапазоне изменения времени нагружения от 1 мин и практически до бесконечности функция ф ( t - т ) может быть аппроксимирована простой зависимостью, линейной относительно логарифма времени нагружения

ф ( t - т ) = 1,46 - 0,122ln( t - т ) ,          (5)

где ( t – τ ) – время нагружения в минутах.

На функцию (5) накладывается ограничение ф ( t - т ) <  1 .

В условиях длительного загружения полные деформации бетона складываются из двух составляющих – линейно-упругой и нелинейной. Линейно-упругая незначительно снижается в соответствии со снижением R_b ( t , т ) , а нелинейная нарастает в результате ползучести бетона. Приращение нелинейной составляющей существенно превосходит соответствующее снижение линейно-упругой во всех практически важных для расчета случаях (нарушение этого соотношения возможно только при очень высоких скоростях нагружения). Такой характер деформирования позволяет предложить для описания роста абсциссы вершины диаграммы-изохроны простую зависимость, аналогичную (4):

£ ь о ⁽ t , т ) = £ ьо ⁽ т ) V ⁽ t ^- т ) ,               (6)

где ^ ( t - т ) = 0,76 + 0,059ln( t - т ) .                (7)

Параметры формулы (2), определяющие форму ветвей диаграммы-изохроны, также выражаются через функции, линейные относительно логарифма времени нагружения: для восходящей ветви

ст , ( t , т ) =

1,25 - 0,1 ^{R b} (t, ^т )- ,        , _{R o}

[0,67 + 0,081 ln ( t - т )] <  2 , (8)

для нисходящей ветви

ст , ( t , т ) =

0,35 + 0,22

R i C t , ! ) R o

[1,2 + 0,048 ln ( t -т )] <  2 , (9)

где R_o = 9,8 МПа.

Зависимости (1)–(9) использованы для построения диаграмм-изохрон высокопрочного модифицированного бетона, реологические свойства которого были экспериментально исследованы в лаборатории проблем прочности и качества в строительстве НИИСФ РААСН. Для изготовления образцов-призм 100 × 100 × 400 мм использовалась бетонная смесь с содержанием цемента 497 кг / куб. м и водоцементным отношением 0,128. Содержание песка и щебня двух фракций составило 707 и 1000 кг / куб. м соответственно. Бетонная смесь модифицировалась введением добавки МБ 10–30С в количестве 109 кг / куб. м. Гидроизолированные образцы-близнецы из бетона одного замеса в возрасте

Физико-механические характеристики бетона

Параметр	R , МПа	Rb , МПа	B *, МПа	Rbn , МПа	Eb , МПа	ε bo ∙ 103
По данным [3]	120	90	94	–	46 670	2,54 ∙ 10–3
По СП 63.13330.2012	–	–	94	70	42 750	2,60 ∙ 10–3

Примечание. * – расчетное значение при коэффициенте вариации 0,135.

Диаграммы-изохроны высокопрочного модифицированного бетона

28 сут. после определения призменной прочности были загружены длительной нагрузкой при двух уровнях напряжений 0,3 и 0,6 от призменной прочности. Прочностные и деформативные характеристики бетона приведены в таблице.

На рисунке показаны расчетно-экспериментальные, по зависимостям (1)–(9), диаграммы-изохроны для трех режимов загружения: 1 – при t – τ = 60 мин, 2 – при t – τ = 100 сут. и 3 – при t – τ = 360 сут. Опытные точки 4 получены путем суммирования линейно-упругих деформаций и деформаций ползучести по данным [3]. Для бетона проектируемых конструкций расчетные диаграммы-изохроны могут быть построены по зависимостям (1)–(9) с использованием нормативных данных СП 63.13330.2012, которые приведены в таблице. В координатах ε – η эти диаграммы практически совпадают с кривыми, полученными расчетно-экспериментальным путем.

Соотношение теоретических и опытных данных показывает, что диаграммы-изохроны, построенные по предлагаемым зависимостям, с достаточной для практических расчетов точностью описывают действительный нелинейный характер деформирования высокопрочного бетона и могут быть рекомендованы в качестве расчетного аппарата при проектировании железобетонных конструкций.

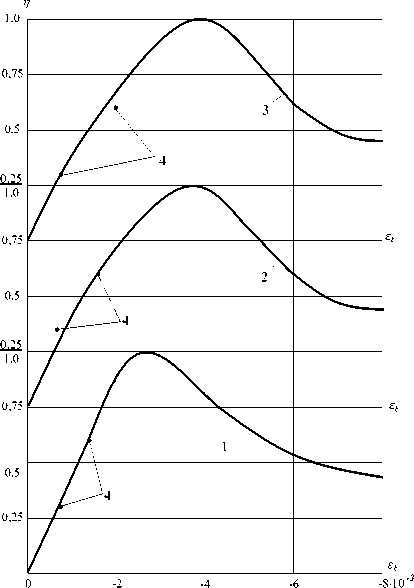
Расчетные диаграммы-изохроны

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.