Диамагнитные структуры - основа квазистационарного медленного солнечного ветра

Квазистационарный и спорадический солнечный ветер (СВ) — это потоки СВ, для которых время жизни источников на Солнце соответственно больше (или много больше) и меньше суток. Квазистацио-нарный медленный СВ в отсутствие спорадических потоков на орбите Земли характеризуется повышенной концентрацией плазмы N >(10±2) см^–3 и относительно небольшой скоростью V ≈250–450 км/с по сравнению с квазистационарным быстрым СВ, истекающим из корональных дыр, максимальная скорость которого V ≈450–800 км/с [Borrini et al., 1981; Eselevich, Fainshtein, 1991, 1992] . Источниками медленного СВ на Солнце являются пояс стримеров [Svalgaard et al., 1974] и цепочки стримеров [Eselevich et al., 1999, 2007] , или псевдостримеры [Wang et al., 2007] . Механизм возникновения медленного СВ до сих пор остается неясным. Спорадический СВ связан с корональными выбросами массы (КВМ), природа которых также находится в стадии изучения.

В работе [Stansby, Horbury, 2018] на расстояниях, меньших или равных 0.5 а.е. от Солнца, по данным космического аппарата Helios в медленном СВ были зарегистрированы локальные концентрации плазмы N > 50 % с одновременным уменьшением магнитного поля В (number density structures). Были проведены статистические исследования 140 таких структур. Они показали, что их пространственный размер составляет ≈ 50÷2000 Мм, что при средней скорости СВ V ≈ 400 км/с соответствует временным масштабам ≈ 2÷80 мин. При этом полное давление (газокинетическое + магнитное) внутри и вне структур сохраняется, что обеспечивает их устойчивость.

В работах [Karlsson et al., 2012, 2015] на расстояниях 1 а. е. от Солнца в медленном СВ были зарегистрированы неоднородности плотности, названные авторами «диамагнитными плазмоидами СВ». Они идентифицировались как локальные повышения концентрации плазмы N > 50 % при одновременном уменьшении модуля магнитного поля В и постоянной скорости V на масштабе (0.1÷10) R E ( R E — радиус Земли). Название «диамагнитный плазмоид СВ» обусловлено антикорреляцией поведения N и В . Постоянство скорости внутри и вне плазмоидов означает, что они сносятся медленным СВ. Временной размер диамагнитных плазмоидов составляет около 5–10 мин [Karlsson et al., 2015] , т. е. примерно согласуется с временными масштабами number density structures, зарегистрированных на расстояниях ≤0.5 а.е. и отмеченных выше [Stansby, Horbury, 2018] .

В работе [Пархомов и др., 2017; Parkhomov et al., 2018] было введено понятие диамагнитных структур (ДС) для квазистационарного медленного СВ, текущего в поясе и цепочках стримеров. Оно имеет более широкий смысл, чем понятие диамагнитных плазмоидов. Основой введения этого определения послужили результаты статей [Еселевич, Еселевич, 2006а, б], в которых было показано, что пояс стримеров представляет собой последовательность лучей повышенной яркости (концентрации плазмы). В каждом из лучей наблюдаются повышение концентрации плазмы N и понижение модуля магнитного поля В, т. е. имеет место диамагнетизм лучей. Лучи сохраняют свой угловой размер ≈2–3° вплоть до 1 а.е. Внутри лучей были зарегистрированы диамагнитные структуры меньших угловых размеров.

Главной задачей настоящей работы является проведение сравнительного анализа, основанного на результатах этого обзора, с целью выяснения природы происхождения термина «диамагнитный плазмоид СВ», который появился в последнее десятилетие в ряде статей.

СТРУКТУРА ПОЯСАИ ЦЕПОЧЕК СТРИМЕРОВОТ СОЛНЦА ДО ОРБИТЫ ЗЕМЛИ

Пояс и цепочки стримеров в белом свете видны как последовательность радиально ориентированных корональных лучей повышенной яркости. Это хорошо видно на рис. 1, где приведены типичные примеры распределений яркости белой короны с вычтенным фоном Π(Λ, R )= Р (Λ, R )– Р S (Λ, R ), построен-

Рис. 1. Распределения яркости с вычтенным фоном П( Л , R )=Р( Л , R )- Р^Л, R ), представляющее собой усреднение Р ( Л , R ) по угловому размеру 5Л=5 ° в полярных координатах ( Л , R ) в двух наиболее простых и характерных ситуациях: верхняя и средняя панели — участки пояса стримеров соответственно в северном и южном полушариях Солнца, расположенные почти в плоскости неба (12 декабря 2000 г., 20:31 UT), W -лимб; нижняя панель — участок пояса, перпендикулярный плоскости неба (5 мая 1996 г., 11:06 UT), W- лимб. Данные LASCO C2

ных по данным коронографа LASCO C2/SOHO для двух предельных наиболее простых случаев: 1) участок пояса стримеров вытянут вдоль широты Λ и расположен, практически, в картинной плоскости (рис. 1, верхняя и средняя панели, соответствующие северному и южному полушариям Солнца, для 12.01.2000); 2) участок пояса стримеров перпендикулярен картинной плоскости (нижнее изображение для 05.05.1996). В этих примерах фоновая яркость Р S (Λ, R ) представляет собой усреднение яркости Р (Λ, R ) по угловому интервалу δΛ=5°.

Особенности структуры пояса и цепочек стримеров от Солнца до Земли, основанные, в том числе, на анализе данных инструмента LASCO С2, представлены на рис. 2 и сводятся к следующему.

• 1.    Пояс стримеров на расстояниях R >3 R _@ ( R _@ — радиус Солнца) от центра Солнца (т. е. выше вершины шлема, отмеченной как helmet apex на нижней панели) в отсутствие КВМ представляет собой последовательность пар лучей (точнее, два близко расположенных ряда лучей) повышенной яркости. Угловой размер всех лучей примерно одина-

  
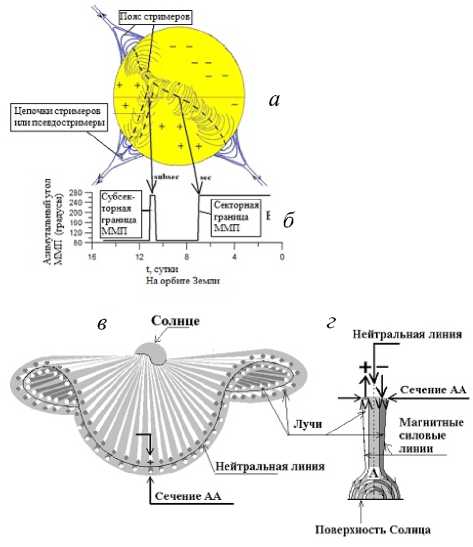
• Рис. 2. — Cхема силовых линий магнитного поля в основаниях пояса и цепочек корональных стримеров, разделяющих области на поверхности Солнца соответственно с противоположной и одинаковой направленностью радиальной компоненты глобального магнитного поля Солнца (а). Одиночная штриховая линия — нейтральная линия (НЛ) радиальной компоненты магнитного поля, проходящая по вершинам арок, двойная штриховая линия — две нейтральные линии вдоль сдвоенных арок магнитного поля в основании цепочек стримеров; б — cхема распределения азимутального угла межпланетного магнитного поля (ММП) на орбите Земли при вращении Солнца вдоль горизонтальной линии (эклиптики) (см. а); в — лучевая структура пояса корональ-ных стримеров в пространстве; г — поперечное сечение (АА) пояса стримеров. В светлых лучах c темным поперечным сечением ряда выше НЛ пояса стримеров магнитное поле направлено от Солнца (+), в темных лучах с темным сечением ряда ниже НЛ — к Солнцу (–). Сплошная линия — нейтральная линия между лучами.

• 2.    Радиальность лучей на расстояниях 10 R _@ > R >(4 + 5) R _@ сохраняется с точностью ± 1.5°. Время жизни наиболее долгоживущих лучей может превышать 10 сут [Eselevich et al., 2001] . Квази-стационарная, т. е. усредненная по колебаниям яркости белой короны с периодами менее суток, лучевая структура пояса стримеров существует всегда: она иногда разрушается под действием КВМ и восстанавливается после этого в течение 1–2 сут [Illing, Hundhausen, 1986] . В поясе стримеров формируется и распространяется от Солнца квазистационарный медленный СВ.

• 3.    Внутри пояса стримеров концентрация плазмы в лучах может превышать концентрацию плазмы между лучами на десятки процентов. В поперечном к плоскости пояса стримеров направлении N может падать в несколько раз [Howard et al., 1975] .

• 4.    Изображения белой короны из-за ограниченности пространственного разрешения современных коронографов не позволяют наблюдать внутреннюю структуру лучей повышенной яркости. Однако методом радиопросвечивания на расстояниях (14+77) R _@ внутри луча пояса стримеров с угловым размером 1.8 ° были обнаружены мелкомасштабные структуры размером до нескольких угловых минут [Woo et al., 1995] .

• 5.    Пояс стримеров охватывает все Солнце в виде волнообразной поверхности (юбки) (рис. 2, в ). В минимуме активности поверхность пояса близка к плоскости солнечного экватора и имеет с ним несколько точек пересечения (две или четыре).

• 6.    Цепочки стримеров (или псевдостримеры) в короне в белом свете выглядят, подобно поясу стримеров, как последовательность пар лучей повышенной яркости (плотности). В них медленный СВ имеет примерно те же свойства, что и в поясе стримеров. Однако цепочки отличаются от пояса тем, что разделяют в короне области с открытыми магнитными силовыми линиями, имеющими одинаковую полярность поля. Поэтому поперечное сечение шлема, расположенного в основании цепочек стримеров, представляет собой две арки (в общем случае — четное число арок) [Eselevich et al., 1999] . Последовательности вершин этих пар арок показаны двумя параллельными пунктирными кривыми на рис. 2, а .

• 7.    На орбите Земли цепочки стримеров регистрируются в виде участков с повышенной концентрацией плазмы, содержащих внутри себя четное число изменений знака ММП, которые называют субсекторными границами (показано стрелкой с надписью subsec на рис. 2, а , б ) [Ivanov et al., 2002] .

• 8.    В ГПС сохраняются угловые размеры и относительные изменения концентрации, наблюдаемые вблизи Солнца в лучевых структурах пояса стримеров [Еселевич, Еселевич, 2006а, б] . На орбите Земли ГПС характеризуется следующими параметрами и особенностями [Borrini et al., 1981; Еселевич, Еселевич, 2006б] :

ков и составляет d ® 2-3°, расстояние между лучами вдоль пояса стримеров — 5–10° [Еселевич, Еселевич, 2006а; Eselevich, Eselevich, 2006] . Здесь и далее угловой размер дается в гелиоцентрической системе координат. Последовательность этих лучей видна на верхней и средней панелях, а поперечное сечение этих двух рядов (Ray+ и Ray–), огибающих шлем с двух сторон на расстояниях R < 3 R 0 , — на нижней панели. Магнитное поле вдоль границы шлема представляет собой арку, два основания которой укоренены на фотосфере [Eselevich et al., 1999] . Яркости лучей в каждой паре в общем случае могут различаться, а направление магнитного поля в них противоположно. Это означает, что нейтральная линия (НЛ) радиальной компоненты глобального магнитного поля Солнца проходит по вершинам шлема вдоль пояса между лучами каждой из пар этих двух рядов. На рис. 2, а шлем показан последовательностью одиночных арок магнитного поля, по вершинам которых проходит НЛ. В общем случае поперечное сечение шлема может состоять из нечетного количества арок магнитного поля (одной или трех).

Продолжение пояса стримеров в гелиосферу (медленный СВ) еще называют гелиосферным плазменным слоем (ГПС) [Winterhalter et al., 1994]. НЛ пояса стримеров внутри ГПС на орбите Земли проявляется в виде секторной границы ММП (показано стрелкой c надписью sec от рис. 2, а к б), разделяющей протяженные области (порядка десятков градусов в гелиоцентрической системе координат или, соответственно, нескольких суток) СВ с противопо- ложными знаками ММП [Korzhov, 1977]. Положительное направление от Солнца соответствует значениям азимутального угла Ф<180°, отрицательное — Ф>180°. Поэтому число изменений знака ММП (если оно больше единицы) в структуре секторной границы является нечетным.

• •    относительно небольшая и почти постоянная по слою скорость СВ V ≈(250÷450) км/с;

• •    пониженная протонная температура T p <10⁵ K;

• •    повышенная концентрация плазмы с максимальными значениями N max >(10±2) см^–3;

• •    антикорреляция изменения плотности N ( t ) и модуля магнитного поля B ( t ) на временных масштабах, по крайней мере, порядка часов и менее;

• •    наличие одного или нескольких изменений знака ММП, являющихся проявлением секторной границы или ее структуры (в случае цепочек стримеров число изменений знака ММП четное, т. е. секторная граница на орбите Земли отсутствует).

Присутствие всех этих признаков обязательно для однозначного определения медленного СВ, текущего в ГПС на орбите Земли.

Поскольку ГПС является квазистационарной структурой, вращающейся вместе с Солнцем, на орбите Земли для нее имеет место следующая связь времени и угловых размеров: 1 сут = 13.3 ° .

По аналогии с [Еселевич, Еселевич, 2006б] введем понятие горизонтального и наклонного участка ГПС. Оно определяется по величине угла наклона X соответствующего ему вблизи Солнца участка НЛ радиальной компоненты глобального магнитного поля относительно линии солнечного экватора. Для построения профиля НЛ, рассчитанной в потенциальном приближении на расстоянии R=2.5R@ от центра Солнца, использовались данные []. Участок ГПС, составляю- щий с плоскостью эклиптики угол X <10°, назовем горизонтальным, а с X>10° — наклонным. Горизонтальный участок ГПС испытывает минимальные искажения при движении составляющего его медленного СВ от Солнца к Земле, так как он не сталкивается с быстрым СВ, истекающим из корональ-ных дыр. В то же время наклонный участок ГПС из-за столкновения с быстрым СВ часто бывает подвержен дополнительному сжатию (в нем усиливается концентрация плазмы и магнитное поле), тем более сильному, чем больше X [Eselevich, Fainshtein, 1991].

Изложенная картина соответствия участков ГПС на 1 а.е. их источникам на Солнце более детально была рассмотрена в [Eselevich et al., 1999; Еселевич, Еселевич, 2006а, б] . Это дает возможность перехода к обоснованию ДС как основы медленного СВ. С этой целью проведем анализ пространственной структуры ГПС на орбите Земли с использованием данных с высоким временным разрешением, полученных на двух космических аппаратах: Wind и IMP-8. При измерении ММП на Wind оно составляет ≈ 3 с, на IMP-8 — ≈12 с .

МЕТОДИКА РАСЧЕТА ВРЕМЕНИ ПРИХОДА НА ОРБИТУ ЗЕМЛИ СТРУКТУР ПОЯСА СТРИМЕРОВ

Момент времени T orb прихода на орбиту Земли данного участка пояса стримеров вблизи Солнца, если этот участок наблюдается на западном лимбе в момент времени Т _W или на восточном лимбе в момент времени Т _Е, определялся по формулам

T orb = т W — 7 сут + A T ; T _хЬ= Т е +7 сут + A T ,     (1)

где

Т W – 7 сут ≈ Т Е + 7 сут                      (2)

— момент времени, когда данный участок пояса стимеров проходит через центральный меридиан.

Здесь 7 сут — это время движения рассматриваемого участка от лимба до центрального меридиана (или наоборот).

Величина A T [Еселевич, Еселевич, 2006б] , определяемая формулой

A T (ч) = (4.640 4 ) / V (км/с),                  (3)

есть время пролета медленного СВ от Солнца до орбиты Земли, V — скорость СВ на орбите Земли. Для V = 350 км/с A T = 5.5 сут. За 1996-1999 гг. было проанализировано около четырех десятков участков квазистационарного медленного СВ, которые на орбите Земли характеризовались параметрами и особенностями, перечисленными выше. Для всех V =350 км/с с точностью до нескольких десятков км/с. Поэтому при расчетах T orb везде полагалось A T = 5.5 сут.

ВЫБОР И АНАЛИЗ СОБЫТИЙ НА РАЗЛИЧНЫХ ВРЕМЕННЫХ (ПРОСТРАНСТВЕННЫХ) МАСШТАБАХ

В качестве исследуемых событий по данным измерений параметров СВ на орбите Земли в соответ- ствии с требованиями, перечисленными выше, выбирались участки ГПС в отсутствие спорадических потоков СВ. Соответствие выбранного участка ГПС поясу стримеров у поверхности Солнца на E- или W-лимбах находилось с помощью формул (1)–(3) в предположении, что параметры СВ рассматриваемого участка пояса стримеров мало меняются в течение ≈12–14 сут.

Событие 4 сентября 1996 г. (день 248)

Этому участку вблизи Солнца соответствует наклонный участок пояса стримеров с X >10 ° . На рис. 3 показаны концентрация N ( t ) и скорость V ( t ) плазмы СВ, параметры ММП, усредненные за 60 с: модуль B ( t ), его компоненты B x ( t ), B y ( t) , B z ( t ) и азимутальный угол Ф ( t ). На профиле Ф ( t ) в момент t ≈ 9 ч видна простая секторная граница, соответствующая изменению угла Ф от =135° до =315°, что равносильно изменению знака радиальной компоненты ММП от «+» (от Солнца) к «–» (к Солнцу). В общем случае секторная граница может быть сложной и состоять из нечетного количества изменений знака ММП.

Возникает вопрос: здесь имеют место колебания N и B во времени или регистрируются квази-статические движущиеся пространственные структуры? Прежде всего, заметим, что в замагниченной плазме возможны колебания магнитного поля двух основных типов, которые при развитии неустойчивости уносят большую часть энергии: альфвеновские

Diamagnetic structures as a basis of the quasi-stationary и магнитозвуковые. В альфвеновских колебаниях N =const, B изменяется, в магнитозвуковых N ( t ) коррелирует с B ( t ). На профиле N ( t ) просматриваются два горба плотности (участки АВ и CD на верхней панели рис. 3 с различными максимальными значениями N , имеющие угловой размер d ≈ 1.5°–1.8°. Они имеют внутреннюю более мелкомасштабную структуру. На границах этих горбов (показаны вертикальными штриховыми линиями) модуль B резко возрастает, а N уменьшается. Наблюдается антикорреляция B ( t ) и N ( t ). Коэффициент антикорреляции на временном интервале 2.5–10.8 ч составляет K ≈–0.81. Не просматривается какая-либо заметная корреляция или антикорреляция между N ( t ) и B x ( t ), B_y ( t ), B_z ( t ). Скорость V практически постоянна (с точностью не хуже, чем ± 10 % на рассматриваемом отрезке времени).

В косых волнах ситуация промежуточная. Так как в нашем случае N ( t ) антикоррелирует с B ( t ), это не колебания замагниченной плазмы, а распространяющиеся от Солнца пространственные структуры.

Прямым доказательством может служить сравнение одновременных измерений на двух разнесенных в пространстве КА Wind и IMP-8 (рис. 4). Для рассматриваемого события 4 сентября 1996 г. средние координаты (в единицах радиуса Земли) КА относительно центра Земли были следующие: для Wind x ≈100, y ≈0; z ≈24; для IMP-8 x ≈24, y ≈–27, z ≈–6. Сравнение проведем для первого пика N (участок АВ

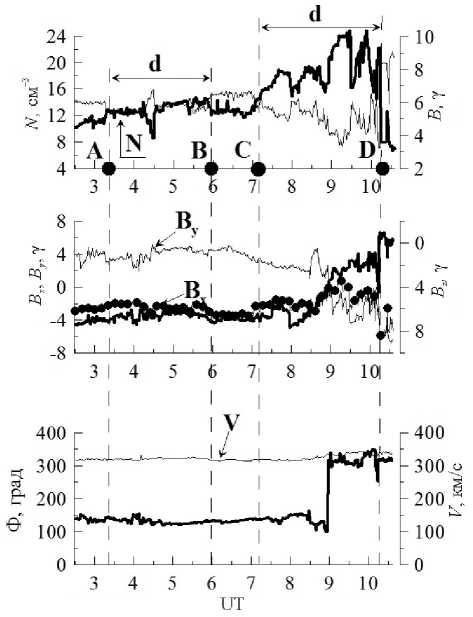
Рис. 3. Параметры солнечного ветра в зависимости от времени 4 сентября 1996 г. (день 248) по данным космического аппарата Wind. Верхняя панель — концентрация плазмы N ( t ) (жирная кривая), модуль ММП B (тонкая кривая); средняя панель — B_x , B_y , B_z ; нижняя панель — азимутальный угол ММП Ф (жирная кривая), скорость плазмы солнечного ветра V _. N , V и B даны примерно с минутным разрешением

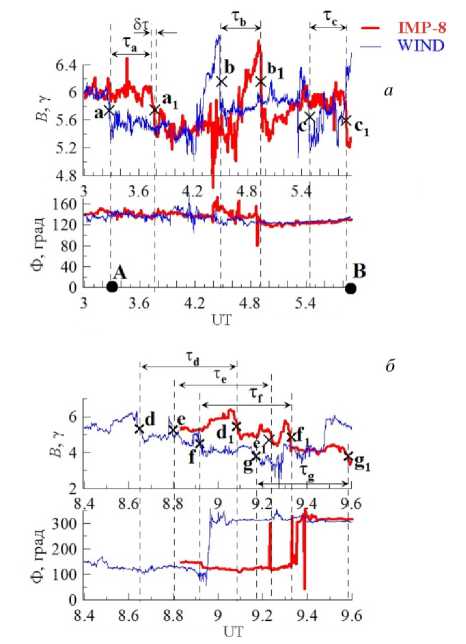
Рис. 4. Модуль В (верхние панели) и азимутальный угол Ф (нижние панели) магнитного поля по измерениям 4 сентября 1996 г. (день 248) двух разнесенных в пространстве космических аппаратов Wind (тонкие кривые) и IМP8 (толстые кривые): а — для участка АВ на рис. 1; б — для части участка CD на рис. 3

на рис. 3) и части второго пика N (части участка СD, так как не для всего СD есть данные IMP-8) на примере магнитного поля В , поскольку оно регистрируется с наилучшим временным разрешением (на Wind ≈ 3 с, на IMP-8 ≈ 12 с). В качестве характерных точек, по которым исследуется движение структур между двумя КА, выберем средние точки токовых слоев (скачков магнитного поля): а и а 1 , b и b 1 , c и c 1 , d и d 1 (рис. 4, а , верхняя панель) и е и e 1 , f и f 1 , g и g₁ (рис. 4, б , верхняя панель). Появление этих слоев в сигнале IMP-8 задерживается по отношению к моменту времени регистрации на Wind на τ ≈25–28 мин. Значения азимутального угла Ф на участках, следующих за каждым из слоев, практически не меняются при движении от КА Wind к IMP-8 (рис. 4, а , б , нижние панели). При этом характерные временные масштабы δτ рассматриваемых скачков магнитного поля (показано на рис. 4, а , верхняя панель), минимальный размер которых может достигать доли минуты, мало меняются за время t >> δτ , т. е. мы имеем дело с распространением квазистатических структур. Поскольку токовые слои ограничивают участки с повышенной плотностью и пониженным магнитным полем (см., например, участки d на рис. 3), мы имеем дело с магнитными трубками: диамагнитный ток на их поверхности приводит к понижению поля внутри трубок. Это согласуется с выводами о том [Еселевич, Еселевич, 2006а, б] , что структуры внутри ГПС являются проявлением лучей повышенной яркости (магнитных трубок) пояса корональных стримеров вблизи Солнца. При этом угловой размер лучевых структур пояса стримеров при движении от Солнца до орбиты Земли сохраняется, что говорит об их квазистационарности на участке пути ≈150 млн. км.

Антикорреляция N ( t ) и B ( t ) при отсутствии заметной антикорреляции N ( t ) с отдельными компонентами ММП в ГПС свидетельствует в пользу того, что эти магнитные трубки вытянуты вдоль направления В . Как отмечалось выше, ослабление поля В внутри трубок является отражением диамагнетизма высокопроводящей замагниченной плазмы с неоднородными границами [Франк-Каменецкий, 1968] . Причина диамагнетизма — диамагнитный (или дрейфовый) ток на граничных поверхностях трубок, который уменьшает поле В внутри трубки. В случае равновесия в направлении, перпендикулярном В , должно сохраняться полное давление Р = N ( T e + T p )+ B ²/8 π . Сохранение полного давления в ГПС ранее уже отмечалось в работе [Winterhalter и др., 1994] . Как будет показано далее, в большинстве случаев на различных участках ГПС это условие выполняется (для рассматриваемого события нет данных о T e ).

В то же время, согласно [Schwenn, March, 1991], в ГПС имеет место развитая альфвеновская турбулентность. Существование квазистатических структур при ее наличии, по-видимому, можно объяснить тем, что уровень турбулентных альфве-новских колебаний (∆В/В)Т много меньше модуля магнитного поля в квазистатических структурах ГПС (∆В/В)К ~ 150–200 %. Турбулентные колебания, возможно, играют роль слабых эффективных соуда- рений, не оказывающих существенного влияния на квазистатические структуры.

Удивительным свойством магнитных трубок в ГПС является наличие внутри них тонкой структуры на нескольких пространственных масштабах.

Действительно, рассмотрим магнитную трубку АВ (обозначение см. на рис. 3) с угловым размером d ≈ 1.5° на более растянутой шкале времени (рис. 5, верхняя панель). Она, в свою очередь, состоит из двух трубок с угловым размером d ₁ ≈ 0.5°–0.7° и одной трубки с d 2 ≈ 0.23°. Последняя трубка состоит из двух трубок с d ₃ ≈ 0.07°. Такая же антикорреляция между N ( t ) и B ( t ) просматривается и на еще меньшем масштабе d ₄ ≈ 0.03° (рис. 5, верхняя панель). Аналогичная ситуация имеет место и на участке CD (рис. 5, нижняя панель). На нем трубка с d ≈ 1.5° содержит внутри четыре трубки с d 2 ≈0.2°–0.3°. При этом, по крайней мере, одна из них (последняя с d 2 ≈0.2°) состоит из трех трубок с d ₃≈0.05°–0.07°. Как показано выше, перечисленные трубки различных масштабов распространяются от Солнца с примерно одинаковыми скоростями, составляя единую структуру ГПС.

Таким образом, проведенный анализ свидетельствует о явлении самоподобия (о подобии геометрии трубок см. ниже), присущего фрактальным образованиям [Milovanov, Zelenyi, 1994, 1999] , а именно, свойства магнитных силовых трубок, соответствующих минимальному угловому размеру d 4 ≈ 0.03° (рис. 5, верхнияя панель), такие же, как и для трубок с масштабом d ≈1.5°–1.8°, т. е. они сохраняются при изменении масштаба примерно в 50–60 раз.

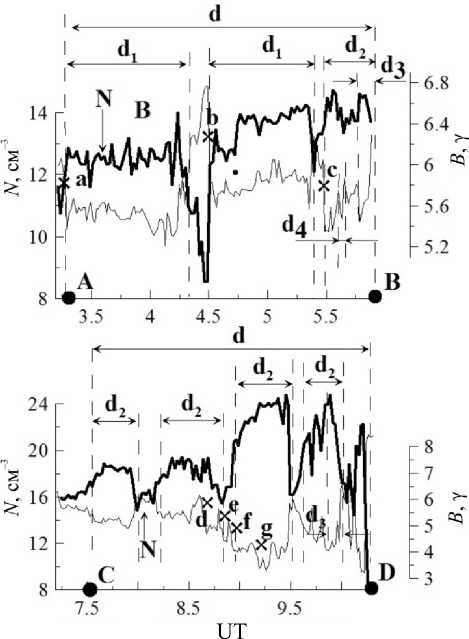
Рис. 5. Те же данные, что на рис. 3 (верхняя панель) для участков дня 4 сентября 1996 гг. (день 248) на более растянутой шкале времени: вверху — участок АВ, внизу — участок CD. Временное разрешение 3 с

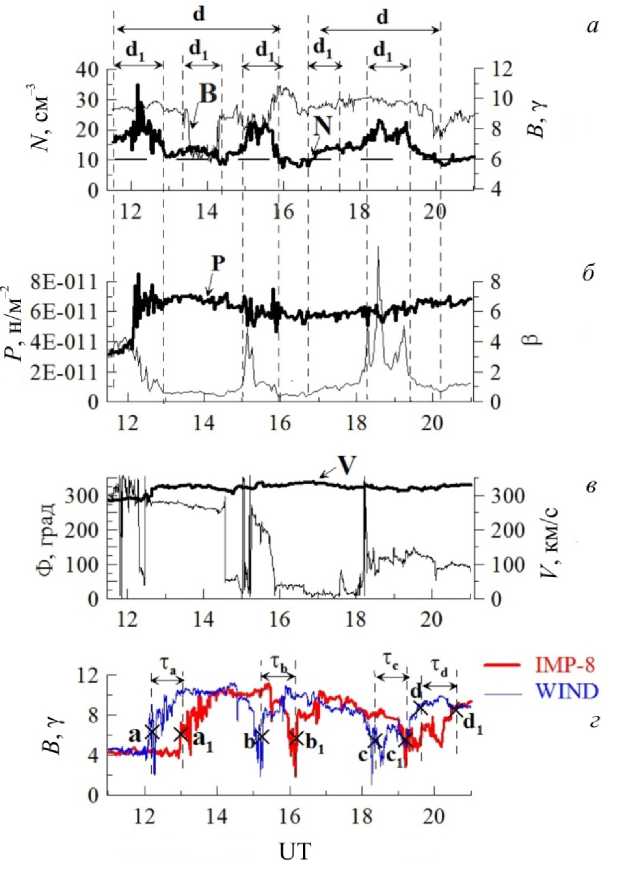
Рис. 6. Параметры СВ в зависимости от времени 15 июня 1999 г. (день 166): а — концентрация плазмы N ( t ) (жирная кривая), модуль В (тонкая кривая) с временным разрешением ≈ 1 мин; б — полное давление Р = N ( T _e+ T _p) + B ²/8 π (жирная кривая) и β = 8 π [ N ( T _e+ T _p )] / B ² (тонкая кривая) с временным разрешением ≈2.5 мин; в — азимутальный угол Ф (тонкая кривая) и скорость СВ V (сплошные кружки) с временным разрешением ≈ 1 мин по данным КА Wind; г ) — модуль магнитного поля В по измерениям на двух разнесенных в пространстве космических аппаратах Wind (тонкая кривая, разрешение ≈ 3 с) и IМP-8 (жирная кривая, разрешение ≈ 15 с)

При этом под свойствами трубок на различных пространственных масштабах понимаются (на примере 4 сентября 1996 г.) следующие:

• •    диамагнетизм (антикорреляция между возрастанием N ( t ) и уменьшением B ( t ));

• •    квазистатичность, по крайней мере, в течение времени их движения между КА Wind и IMP-8;

• •    примерное сохранение в направлении, перпендикулярном В , полного давления Р = N ( T e + T p )+ + B ²/(8 π ).

• •    повышенное значение β =8 π N ( T _e+ T _p)/ B ² внутри трубок по сравнению с окружающей их плазмой.

Для 4 сентября 1996 г. два последних свойства невозможно проверить из-за отсутствия данных по электронной температуре Т е .

Поэтому рассмотрим участок ГПС на орбите Земли во второй половине 15 июня 1999 г. (день 166), для которого есть данные о Те. Этому событию вблизи Солнца соответствует участок пояса стримеров, пересекающий плоскость эклиптики почти вертикально (см. нейтральную линию на синоптической карте CR 1950 [] на долготе 210°–220° (9–10 июня 1999 г.)). На рис. 6, а, видно, что B(t) и N(t) изменяются в противофазе (K ≈ –0.8). Наблюдаются две области повышенной концентрации Nmax >10 см–3 с угловыми размерами d≈ 2.5° и d≈ 1.7°. Между областями проходит сложная (с несколькими изменениями знаков ММП) секторная граница в конце 15 июня (рис. 6, в). B(t) и N(t) изменяются в противофазе (коэффициент антикорреляции K ≈ –0.8). Скорость V (черные кружки) практически постоянна на всем рассматриваемом интервале. Внутри этих областей просматривается более мелкомасштабная структура (пики Nmax>10 см–3) с характерным угловым размером d1 ≈ 0.6°–0.8°. Внутри пиков с размером d1 наблюдаются пики с d2 ≈ 0.15°–0.20°,

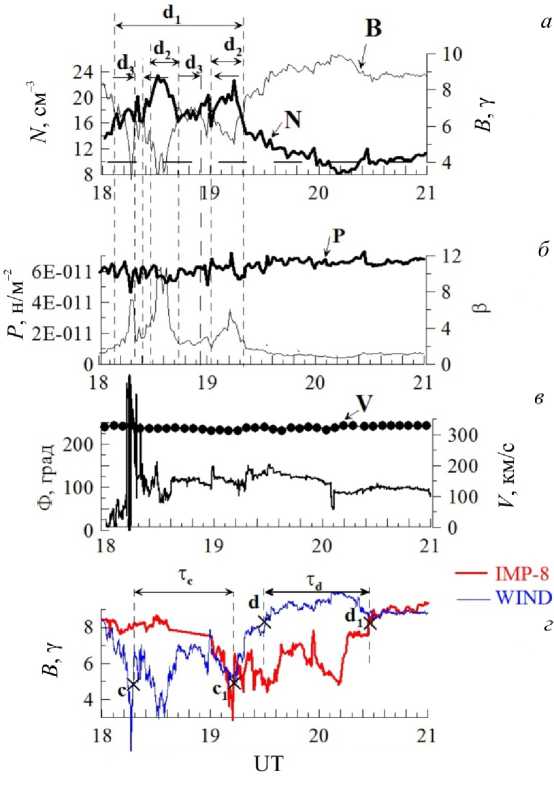
Рис. 7. Те же данные, что на рис. 6, для части дня 15 июня 1999 г. (день 166) на более растянутом временном масштабе. Данные на панелях а , б и скорости V на ( в ) нанесены с временным разрешением ≈1 мин, все остальные — с разрешением ≈15 с

а внутри последних — пики с d ₃ ≈ 0.03°–0.04°. Это следует из рис. 7, а , на котором область с d ≈1.7° дана на более растянутом временном масштабе. Для каждого из пиков любого указанного углового размера d n B ( t ) и N ( t ) изменяются в противофазе (рис. 6, а и 7, а ), величина β в области пиков N заметно, а часто в разы превышает его значения вне пиков (рис. 6, б и 7, б , тонкая линия).

Полное давление Р = N ( T e + T p ) + B ²/(8 π ), усредненное по колебаниям с периодом τ ≤ 10 мин, внутри и вне пиков мало меняется (рис. 6, б и 7, б , жирная кривая). На всем рассматриваемом интервале на масштабе пиков с угловым размером d ≈ 1.7°–2.5° полное давление также сохраняется с точностью, не хуже, чем ± 15 %.

Токовые слои, связанные с границами наиболее крупных пиков Nmax>10 см–3, обозначены буквами а, b, c, d и а1, b1, c1, d1 при регистрации на КА Wind и IMP-8 соответственно (рис. 6, г и 7, г). Времена задержки прохождения этих структур между КА τa ≈ 58 мин, τb ≈53 мин, τc ≈54 мин, τd≈52 мин, т. е. близки по величине. Это означает, что весь набор структур движется как единое образование примерно с одной скоростью. Все это свидетельствует о том, что пики Nmax>10 см–3 с угловыми размерами d, d1, d2, d3 и т. д. являются диамагнитными трубками, причем трубки меньшего размера заполняют трубки большего размера.

Выделенные на приведенных двух примерах характерные особенности поведения параметров ГПС на орбите Земли обнаруживаются, в той или иной степени, на любом участке ГПС в отсутствие спорадических потоков. Этот вывод сделан по результатам рассмотрения около 40 событий 1996–1999 гг. Здесь следует отметить, что для понятия фракталь-ности важным является самоподобие вложенных диамагнитных трубок. Покажем это для исследованных участков ГПС путем следующих рассуждений .

Пусть большая диамагнитная трубка заполнена диамагнитными трубками меньших поперечных размеров. Большую и маленькие трубки можно считать самоподобными, если их поперечные сечения по форме одинаковы и близки кругу. В пользу того, что в нашем случае это должно быть так, свидетельствуют следующие положения.

• 1.    Углы наклона в 40 исследованных участках ГПС по отношению к плоскости эклиптики были разными. Это означает, что магнитные трубки пересека-

  

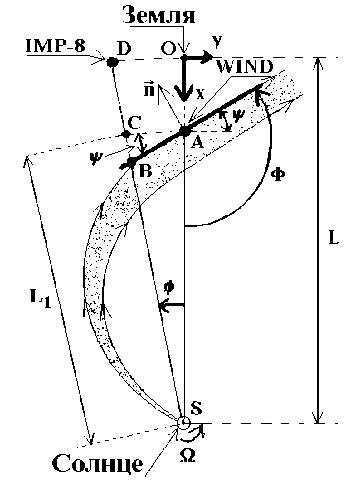
  Рис. 8. Сечение плоскостью эклиптики пояса стримеров и его продолжения в гелиосфер

  
  

• 2.    Общие физические соображения: маловероятно, чтобы сечения диамагнитных трубок были в виде эллипса или любой другой фигуры.

лись КА под разными произвольными углами. И все они дали примерно один и тот же результат: угловые размеры вложенных друг в друга магнитных трубок меняются от d ≈ 1.5°–3.0° до минимальных размеров d ≈ 0.03°–0.06° (рис. 5, верхняя панель). Это означает, что поперечные сечения трубок близки кругу.

СХЕМА ПОЛОЖЕНИЯ ДИАМАГНИТНЫХ ТРУБОК В ГЕЛИОСФЕРЕ И ОПРЕДЕЛЕНИЕ СКОРОСТИ ИХ ДВИЖЕНИЯ ОТ СОЛНЦА

На основании изложенного в предыдущем параграфе cечение пояса стримеров и его продолжения в гелиосфере плоскостью эклиптики схематично может быть представлено в виде сечения плоскостью эклиптики диамагнитной трубки, содержащей движущуюся плазму повышенной по отношению к окружающей плазме концентрации. Вблизи Солнца трубка ориентирована радиально, а по мере удаления от него постепенно изгибается в направлении против вращения Солнца. Ее угловой размер d остается примерно постоянным на всем протяжении от Солнца до Земли. Очевидно, что на любом расстоянии от Солнца трубка ориентирована вдоль силовых линий ММП, которые ее образуют (кривые линии со стрелками, ограничивающие область с точками на рис. 8). Поэтому на орбите Земли угол наклона оси трубки к направлению оси ОX, так же как линия ее переднего фронта (жирная линия АВ на рис. 8), будет равен азимутальному углу Φ линий ММП. Из-за повышенной концентрации плазмы внутри трубка представляет собой пространственную неоднородность по отношению к окружающей ее плазме. При этом плазма СВ движется радиально везде в плоско- сти эклиптики как в области неоднородности, так и вне ее. Квазистационарная картина такого радиального течения СВ с пространственными неоднородностями в распределении концентрации плазмы в плоскости эклиптики вращается вместе с Солнцем и имеет на орбите Земли линейную скорость V0=2nL/T =2n215R JT = 405 км/с, T =27 сут. Учитывая наличие этих двух независимых движений в плоскости эклиптики, получим формулы для вычисления угла ΦC наклона фронта АВ трубки с плазмой медленного СВ, имеющего на орбите Земли скорость V, и время задержки τС прохождения фронтом АВ КА Wind (точка А) и IMP-8 (точка D), указанных на рис. 8.

Пусть в момент времени t 0 =0 источник плазмы медленного СВ находился на центральном меридиане Солнца ( ϕ =0°). Частицы плазмы, вылетающие из источника в этот момент, будут двигаться радиально вдоль линии SA (или OX). В момент времени t << T из-за вращения Солнца источник медленного СВ будет располагаться относительно центрального меридиана под углом ϕ <<360°. Испускаемые им частицы будут двигаться радиально вдоль линии SВ. Из геометрии картины на рис. 8 следует, что

τ _C

φ T L - L y - y x - x

+        ¹ ≈        ¹ +        ¹

2π V      V _O V

Здесь было учтено, что Φ=2π( y – y 1 )/ L , где x , y и x 1 , y 1 — координаты (c учетом знака) положений КА IMP-8 (точка D) и Wind (точка А) соответственно.

Угол ψ наклона фронта АВ относительно линии АС (рис. 8) с учетом неравенства L – L 1 << L определяется формулой:

CB φ TV 2π V tgψ =≈= .

CA  2πφ L V ₀

Искомый азимутальный угол Φ _C связан с углом

ψ соотношениями

Φ C = 90° + ψ , если Φ C < 180°, (3)

Φ C = 270° + ψ , если Φ C > 180°. (4)

Поскольку для ГПС на орбите Земли V ≈350 км/с ± 50 км/с, для квазистационарной диамагнитной трубки угол Φ _C≈130° ± 5°, либо Φ _C≈310° ± 5°.

Для проверки изложенной выше картины сопоставим рассчитанные величины τ _С, Φ _C с измеренными τ _m, Φ _m. Проведем это сравнение на примере уже рассмотренного события 4 сентября 1996 г.

Измеренные значения Φ _m (для токового слоя а Φ _m= Φ _а, для токового слоя b Φ _m= Φ _b и т. д.) находились по формуле Φ _m=( Φ + Φ ₁) /2, где Φ и Φ ₁ — усредненные значения азимутального угла по интервалу времени 3 мин непосредственно перед прибытием токового слоя на КА Wind и IMP-8 соответственно. Обычно Φ и Φ 1 близки по величине. На верхних панелях рис. 4, а , б местоположения токовых слоев отмечены крестиками с соответствующей буквой. Время движения слоя между двумя КА обозначены τ с индексом, соответствующим букве слоя. В качестве V бралась средняя величина скорости СВ на пути движения каждого из слоев между двумя КА. Измеренные V , τ _m, Φ _m приведены в столбцах 9, 10, 12 таблицы. Результаты рассчитанных значений τ _С, Φ _C по формулам (1)–(4) для средних точек токовых слоев (скачков магнитного поля), регистрируемых последовательно на Wind и IMP-8 (с индексом 1): а и а 1 , b и b 1 , c и c 1 , d и d 1 , е и e 1 , f и f 1 , g и g 1 на рис. 4, а , б приведены в столбцах 11 и 13 таблицы.

Для рассматриваемого интервала времени координаты Wind (столбцы 3–5 таблицы) и IMP-8 (столбцы 6–8) были соответственно

Wind: x ≈ 100 R E , y ≈ 0, z ≈–3 R E ;

IMP-8: x ≈ 24 R E , y ≈ –27 R E , z ≈–6 R E , Φ m = Φ а .

Подставляя координаты спутников и значения V и V 0 для точек a–g в формулы (1)–(4), находим рассчитанные значения τ С и Φ C для рассматриваемых слоев, приведенные в столбцах 11 ( τ С ) и 13 ( Φ C ). Результаты хорошо согласуются с наблюдаемыми значениями. При этом среднее время задержки для всех семи слоев τ a ≈ 25 ± 1.3 мин. Таким образом, с точностью ≈5 % скорость всех слоев оказывается одинаковой, т. е. вся фрактальная структура распространяется как единое образование.

Аналогичным способом исследовано 18 событий (см. таблицу). Отношения τ m / τ c в зависимости от нормированного расстояния между КА I / R E показаны на рис. 9.

Средние арифметические отклонения от линий τ _m / τ =1 и Φ _m / Φ _c=1 составляют соответственно ≈15 % и ≈5 %. Таким образом, предложенная выше картина распространения квазистационарной диамагнитной трубки с плазмой в СВ неплохо согласуется с экспериментом.

АНАЛИЗ УСТОЙЧИВОСТИ ТОКА НА ГРАНИЦАХ ДИАМАГНИТНЫХ ТРУБОК

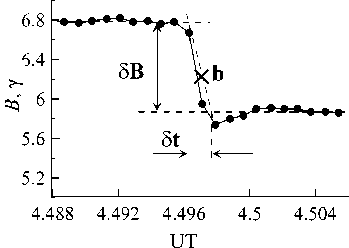
Как уже отмечалось выше, на границах диамагнитных трубок существует скачок модуля магнит- ного поля δВ на пространственном масштабе ∆, а значит существует связанный с ним диамагнитный (или дрейфовый) ток. На рис. 10 показаны два примера таких скачков для двух различных событий: 4 сентября 1996 и 18 июня 1998 г.

Остановимся более подробно на последнем событии, для которого известны все необходимые параметры в области скачка (точка С): V ≈ 350 км/с, Φ ≈300°, ψ ≈30°, T e ≈1.4·10⁵K, Т р ≈3·10⁴K, N ≈30 см^–3, B ≈11 γ = 1.1·10^–4 G. Прежде всего, оценим толщину токового слоя ∆ , зная его временную ширину δ t .

Величина ∆ ≈ V cos ψδ t ≈912 км. Сравним ∆ с величиной ионного ларморовского радиуса ρ i ≈ v tp / ω hp .

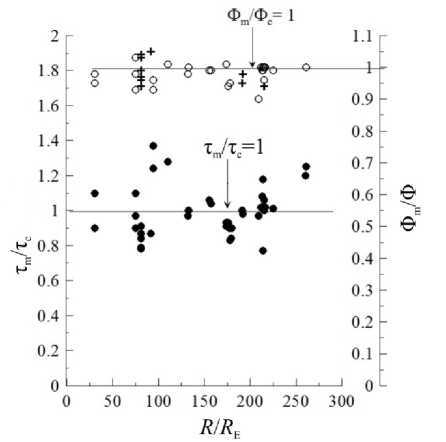
Pис. 9. Отношения τ _m / τ _c (сплошные кружки) и Φ _m/ Φ _c (светлые кружки — для Φ m > 180°, крестики — для Φ m <180 ° ) в зависимости от нормированного расстояния I / R _E между КА

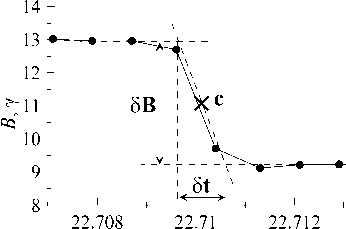
UT

Рис. 10. Примеры скачков магнитного поля В с максимальным временным разрешением (точки на графике нанесены с интервалом три секунды) для двух событий на орбите Земли по данным Wind: 4 сентября (день 248) 1996 г. (вверху); 18 июня (день 169) 1998 г. (внизу)

День	t 0 ,	Координаты местоположения КА						V ,	τ m ,	τ c ,	Φ m ,	Φ C ,
	часы	Wind			IMP-8			км/с	мин	мин	град	град
		x / R E	y / R E	z / R E	x / R E	y / R E	z / R E
19.05.1996	7.50	102	–34	4	–21	10	–16	327	27	28	307	309
(день 140)	7.96							327	28	28	310	309
15.07.1996	13.50	195	13	–4	25	–18	5	380	47	57	300	315
(день 197)	14.70								48	57
	16.75								51	57
04. 09.1996	3.30	100	0	24	24	–27	–6	320	28	31	134	128
(день 248)	4.50							320	27	31	132	128
	5.47							320	24	31	127	128
	8.64							340	26	30	122	130
	8.80							340	26	30	125	130
	8.92							340	26	30	125	130
	9.16							340	25	30	125	318
03.11.1996 (день 308)	19.4	114	–32	5	6	–27	–16	325	46	36	317	308
04.11.1996	1.44	110	–26	6	20	–15	–18	360	31	25	300	312
(день 309)	2.41							375	33	24	290	313
04.04.1997	0.50	220	5		13	–23	18	410	60	62	286	314
(день 94)
03.09.1997 (день 246)	15.60	80	33	0	23	–25	–15	390	21.6	27.8	131	135
23.02.1997	9.74	210	15		–10	–30	–15	480	61	60	315	318
(день 54)
02.03.1998	6.60							400	66	55	315	–
(день 61)	8.15							420	64	51	316	315
10.03.1998	5.30	233	–21	–23	24	15	14	320	71	60	–	–
(день 69)	8.50							370	54	51	120	127
	12.00							430	51	51	305	317
21.03.1998	11.4	232	–24	–15	20	0	–15	400	54	50	310	315
(день 80)	12.55							420	36	47	316	316
16.04.1998	20.25	223	–13	13	32	0	15	350	55	55	125	131
(день 106)	21.20							350	54	55	128	131
18.06.1998	4.0	77	62	14	35	0	–15	340	29	30	325	317
(день 169)	9.4							340	33	30	300	317
	22.7							340	27	30	310	317
10.07.1998 (день 191)	22.85	80	15	3	0	–28	16	325	33	37	135	129
01.06.1999	13.60	178	–21	–12	23	–23	2	350	50	47	311	315
(день 152)	15.10							350	49	47	311	315
08.06.1999	1.65	195	–21	–10	–11	31	–11	345	51	50	310	310
(день 159)	5.60							360	51	50	310	312
	8.05							360	51	50	132	132
	10.20							365	51	50	132	132
15.06.1999	12.50	205	–21	–8	33	–13	16	290	58	62	310	306
(день 166)	15.90							330	53	58
	20.20							330	54	58	120	128
	22.30							330	52	58
26.09.1999	15.00	61	13	3	33	4	–5	400	8	10	300	315
(день 269)	20.25							460	10	9	310	317

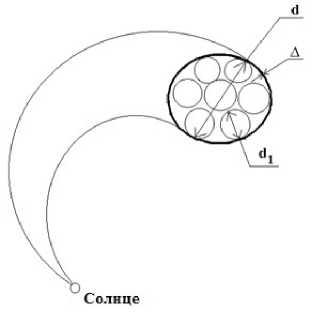
Рис. 11 . Схема фрактальной структуры диамагнитной трубки в СВ по результатам исследований данной работы

Найдем v tp ≈25 км/с — тепловую скорость протонов и ω hp ≈1.1 с^–1 — ларморовскую частоту протонов. Отсюда ρ i ≈23 км. Таким образом, ∆ ≈40 ρ i . Однако это значение следует считать верхней границей значения ∆ , поскольку наблюдаемая минимальная временная ширина скачка δ t ограничена временным разрешением метода измерений ~3 с, а значит истинное значение δ t должно быть меньше.

Сделаем анализ устойчивости дрейфового тока на границе трубки. Известно, что развитие бунема-новской неустойчивости становится возможным, если выполняется условие [Михайловский, 1970] :

v d > v tp                                                 (5)

Величину v d оценим из соотношения:

δBc vd ≈       ≈0.54 км/с,                        (6)

4πe∆ где с=3·105 км/с, e=4.8·10–10 ед. CGSE, δВ≈3·10–5 G. Отсюда vd≈0.54 км/с << vtp≈25 км/с.

Таким образом, наблюдаемые дрейфовые токи на границах трубок устойчивы по отношению к раскачке различного типа электростатических и электромагнитных колебаний. Этим, возможно, и объясняется существование в СВ перемещающихся в пространстве квазистационарных диамагнитных трубок с плазмой повышенной плотности.

Схематично фрактальная структура диамагнитных трубок СВ показана на рис. 11. Аналогичная структура для СВ была теоретически получена в работе [Mi-lovanov, Zelenyi, 1994, 1999] .

При дальнейшем изложении вместо выражения диамагнитные трубки будем использовать более общий термин — диамагнитные структуры (ДС). Он был введен и использован при анализе взаимодействия участков ГПС с магнитосферой Земли в статье [Parkhomov et al., 2018] .

СРАВНЕНИЕ НАБЛЮДЕНИЙ ДИАМАГНИТНОГО ПЛАЗМОИДА СВ И ДИАМАГНИТНЫХ

СТРУКТУР ГПС

Перейдем к рассмотрению главной задачи приведенного выше обзора работ по структуре медленного СВ, решение которой до сих пор оставалось неяс-

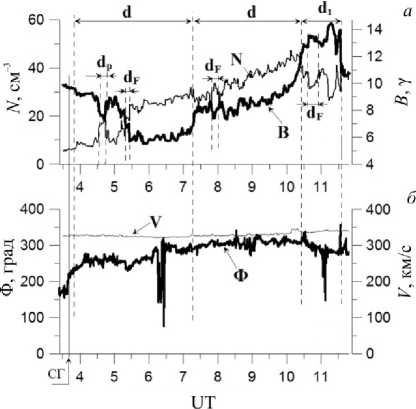
Рис. 12. Параметры СВ в зависимости от времени 5 апреля 2006 г.: а — концентрация плазмы N(t) (жирная кривая), модуль В (тонкая кривая) с временным разрешением ≈1 мин; б — азимутальный угол Ф (жирная кривая) и скорость солнечного ветра V (тонкая кривая) с временным разрешением ≈1 мин. Данные КА Wind. Положение секторной границы слева показано вертикальной линией со стрелкой внизу и отметкой СГ ным. Она касается понимания морфологии и природы происхождения в медленном СВ ранее обнаруженных особенностей: локальных повышений плотности (number density structures) на временных масштабах Δt≈2÷80 мин [Stansby, Horbury, 2018] и диамагнитных плазмоидов СВ (diamagnetic plasmoid SW) на Δt≈5÷10 мин [Karlsson et al., 2015]. Как уже отмечалось во введении, number density structures, регистровались на расстояниях ≤0.5 а.е. [Stansby, Horbury, 2018]. Они, также как диамагнитные плазмоиды СВ были диамагнитны, имели близкий к ним временной размер и регистрировались в медленном СВ. Поэтому в дальнейшем при анализе оба типа структур будем называть диамагнитными плазмоидами СВ.

Рассмотрим типичный участок ГПС на орбите Земли 5 апреля 2006 г. (день 96) в 04:35–04:55 UT.

Как видно из рис. 12, а , профили B ( t ) и N ( t ) изменяются в противофазе ( K ≈–0.8). Весь участок ГПС складывается из трех диамагнитных структур повышенной концентрации N max >(10±2) см^–3, две из которых имеют угловой размер d ≈2°, а одна d 1 ≈0.7°. Секторная граница располагается в начале первого участка d в момент времени 3.7 ч 5 июня ( б ). Скорость V практически не меняется на всем рассматриваемом интервале. Внутри этих трех диамагнитных структур наблюдаются усиления плотности (внутренние ДС) различных меньших масштабов, отражающие фрактальность ДС медленного СВ. Несколько из этих ДС показаны горизонтальными стрелками и обозначены d F на рис. 12, а . Диамагнитный плазмоид СВ, исследованный в статье [Karlsson et al., 2015] и отмеченный как d F , очевидно, является одним из этих внутренних элементов фрак-тальности диамагнитной структуры с угловым размером d ≈2° рассматриваемого участка ГПС.

Аналогичный сравнительный анализ, проведенный еще для двух диамагнитных плазмоидов СВ из статьи [Karlsson et al., 2015] для дат 04.04.2004 и 11.03.2003, приводит также к подобному выводу.

Таким образом, можно достаточно уверенно утверждать, что в отсутствие спорадических потоков диамагнитные плазмоиды СВ, исследованные в статье [Karlsson et al., 2015] , являются внутренними элементами фрактальных диамагнитных структур медленного СВ.

ВЫВОДЫ

• 1.    Источником медленного квазистационарного СВ на Солнце являются пояс и цепочки стримеров. Пояс стримеров охватывает все Солнце в виде волнообразной поверхности (юбки) и представляет собой последовательность пар лучей повышенной яркости (концентрации плазмы) или два близко расположенных ряда лучей. Нейтральная линия радиальной компоненты глобального магнитного поля Солнца проходит между лучами каждой из пар вдоль пояса. Продолжением пояса стримеров в гелиосферу является гелиосферный плазменный слой (ГПС).

• 2.    Лучи повышенной яркости пояса стримеров на орбите Земли, т. е. в ГПС, являются диамагнитными трубками с плазмой повышенной концентрации плазмы ( N _max>(10±2) см^–3) и пониженным значением межпланетного магнитного поля. Они так же обладают тонкой структурой на нескольких пространственных масштабах (фрактальностью), начиная примерно с 1.5°–3.0° и кончая минимальным масштабом ≈0.03°–0.06°, т. е. угловой размер вложенных друг в друга трубок меняется почти на два порядка.

• 3.    Магнитные трубки на каждом наблюдаемом пространственном масштабе диамагнитны, т. е. на их поверхности течет диамагнитный ток, уменьшающий магнитное поле внутри трубки и увеличивающий его вне ее. При этом величина β =8 π [ N ( T _e+ T _p)]/ B ² внутри трубки превышает значение β вне ее.

• 4.    Во многих случаях полное давление Р = N ( T e + T p )+ B ²/(8 π ) практически постоянно в трубках и вне их на любом из указанных выше масштабов.

• 5.    Магнитные трубки являются квазистатиче-скими структурами и практически не меняются при движении ГПС между двумя разнесенными в пространстве КА. Сохранение трубками ГПС углового размера при движении от Солнца до орбиты Земли свидетельствует об их квазистационарности на всем этом пути.

• 6.    Дрейфовый (или диамагнитный) ток на границе трубок устойчив по отношению к раскачке хаотических колебаний в замагниченной плазме. Все это позволяет ввести более общее название этих трубок — диамагнитные структуры (ДС), составляющие основу медленного СВ или ГПС на орбите Земли.

• 7.    Обнаруженные и исследованные ранее в статьях [Karlsson et al., 2015; Stansby, Horbury, 2018] диамагнитные плазмоиды СВ являются мелкомасштабной (по времени и пространству) составляющей фрактальных диамагнитных структур медленного СВ.

Эти шесть выводов отражают основы современного понимания природы и структуры медленного СВ на всем протяжении от Солнца до орбиты Земли. Проведенный в конце данной статьи сравнительный анализ, основанный на этих выводах, позволил выяснить морфологию и природу происхождения нового термина «диамагнитные плазмоиды» СВ (или локальные повышения плотности), который появился в ряде статей за последнее десятилетие. Полученный при этом новый результат сформулирован в выводе 7.

Автор выражает благодарность Ю.И. Ермолаеву, по инициативе которого была подготовлена данная статья. Автор благодарит также команды LASCO/ SOHO, Wind, IМP8, данные которых использовались в работе.

Работа выполнена в рамках Государственного задания № 007-00163-18-00 от 12.01.2018.