Диаметр светового пятна в ближней зоне бинарного дифракционного микроаксикона

Известно, что с помощью аксикона можно сформировать на определенном участке оптической оси лазерный бездифракционный пучок Бесселя. Интерес к таким пучкам не ослабевает. В [1] с помощью световода диаметром 30 мкм с кольцевым сечением из плавленого кварца (толщина кольца 3 мкм), на конце которого была помещена линза с радиусом кривизны 70 мкм, сформирован Бесселев пучок диаметром 20 мкм и протяженностью 500 мкм (длина волны λ = 1,55 мкм). В [2] FDTD-методом моделировался 2D фотонный кристалл из прямоугольной сетки диэлектрических стержней в форме аксикона: основание 20a, высота аксикона 10a, показатель преломления стержней n = 3,13, радиус стержней 0,22a, длина волны λ = a/0,36, a – период решетки стержней. Показано, что на расстоянии z < 30a формируется расходящийся Бесселев пучок с диаметром по полуспаду интенсивности FWHM = 1,5λ. В [3] экспериментально с помощью радиально-поляризованного лазерного пучка (λ = 532 нм), конического аксикона и иммерсионной микролинзы с числовой апертурой NA = 1,25 в серебряной пленке толщиной 50 нм (с диэлектрической проницаемостью ε = -10,1786 - i 0,8238) сформирована поверхностная плазмонная волна в виде концентрических колец, описываемых функцией Бесселя первого порядка. Диаметр центрального осевого кольца – 278 нм, толщина – 250 нм ≈ 0,5 λ. Картина поверхностного плазмона наблюдалась в микроскопе ближнего поля Veeco Aurora 3 с разрешением 50 – 100 нм. Аналогично в [4] с помощью He-Ne лазера (λ = 632, 8 нм), излучающего радиально-поляризованный свет, аксикона и иммерсионной линзы с NA = 1,4 в пленке золота толщиной 44 нм (ε = 0,3 + i 3,089) формировался поверхностный плазмон с фокусной точкой в центре диаметром FWHM = 0,22 мкм=0,35 λ. Плазмон наблюдался с помощью латексного шара диаметром 175 нм.

В [5,6] исследовалась фокусировка лазерного света вблизи кольцевой структуры на металле. В [5] FDTD-методом проведено моделирование фокусировки зонной пластинки с радиусом колец rn2 = 2nf λ + n2λ2, f = 1 мкм, λ = 633 нм, выполненной в тонких пленках серебра (50 нм) и золота (50 нм), напыленных на кварце. Диаметр кольцевой структуры 13 мкм. Показано, что на расстоянии z = 1,5 мкм от пластины возникает фокальное пятно диаметром по полуспаду FWHM = 0,3 λ (полная ширина пятна – 0,7 λ). В [6] экспериментально исследованы аналогичные кольцевые структуры (диаметр 8 мкм) в пленке золота (100 нм). В микроскоп ближнего поля NTEGRA (NT-MDT) с разрешением 100 нм на расстоянии z = 1,6 мкм наблюдалось фокальное пятно диаметром по полуспаду интенсивности FWHM = 1,7 λ (полный диаметр 5λ), λ = 633 нм, хотя теория предсказывает размер фокального пятна FWHM = 0,5λ. В [7] с помощью 8 отверстий, выполненных симметрично по кругу диаметром 200 нм (диаметр круга 1 мкм) в PMMA резисте на стекле, в некогерентном свете с длиной волны λ = 650 нм на расстоянии 500 нм от поверхности зарегистрировано фокальное пятно диаметром FWHM = 0,4 λ (полный диаметр 1,2 λ). В [8] на пленке аморфного кремния толщиной 120 нм реализована линза Френеля с фокусным расстоянием f = 5 мкм и диаметром 50 мкм для длины волны λ = 575 нм (26% пропускания). В иммерсии линза имела числовую апертуру NA = 1,55 и фокусировала свет в фокальное пятно диаметром FWHM = 0,9 λ. Интересно, что измерено это пятно было с помощью флуоресцентной сферы с диаметром 0,5 мкм.

Известны также работы, в которых теоретически [9] и экспериментально [10] исследовалась фокусировка света в ближнее поле с помощью бинарного дифракционного аксикона. В [9] была разработана приближенная теория, которая хорошо описывает дифракционный аксикон с периодом колец T < 5 λ. В этом случае бинарный аксикон можно рассматривать как дифракционную решетку, если центральную часть аксикона закрыть непрозрачным диском. Показано, что для аксикона с периодом T = 5 λ, радиусом 40 λ на расстоянии 40 λ от поверхности аксикона диаметр фокального пятна будет равен FWHM = 0,88 λ. В [10] экспериментально исследовался бинарный акси-кон (диаметр 30 мм) с периодом T = 33 мкм (он соответствует коническому аксикону из стекла с углом при вершине 88°), выполненный на резисте ZEP520A (показатель преломления n = 1,46). Было показано, что диаметр лазерного пучка не зависит от длины волны и что на расстоянии от 0 до z = 50 мм радиус Бесселева пучка растет от 1,2 мкм (λ = 532 нм) до 12,5 мкм и далее от z = 50 мм до z = 100 мм сохраняет этот радиус.

В данной работе исследовались бинарные аксико-ны с периодом 4, 6 и 8 микрометров, изготовленные по технологии фотолитографии с разрешением 1 мкм, глубиной 500 нм и диаметром 4 мм. Экспериментально показано, что в ближней зоне дифракции вдоль оптической оси на расстоянии до 40 мкм от ак-сикона появляются фокальные пятна с диаметром от 3,5 λ до 4,5 λ (для аксикона с периодом T = 4 мкм) и от 5 λ до 8λ (для аксикона с периодом 8 мкм), λ – длина волны света (λ = 0,532 мкм). Причем первый фокус возникает на расстоянии 2 мкм ( T = 4 мкм), а фокальные пятна появляются с периодом 2 мкм (для T = 4 мкм) и 4 мкм (для T = 8 мкм). Осуществлено также моделирование дифракции плоской и расходящейся линейно-поляризованных световых волн с помощью программ FullWAVE (RSoft) и оригинальной программы R-FDTD, реализующих разностные методы решения 3D уравнений Максвелла в декартовой и цилиндрической системе координат. Полученные численные значения диаметров фокальных пятен на оптической оси в ближней зоне дифракции для ак-сикона с периодом T = 4 мкм согласуются с экспериментальными данными.

Для анализа поля вблизи оптической оси и вблизи аксикона нельзя воспользоваться электромагнитной теорией [9], т.к. в центральной части аксикон нельзя считать дифракционной решеткой.

Пусть на аксикон падает плоская волна с линейной поляризацией, тогда в начальной плоскости z = 0, совпадающей с выходной поверхностью аксикона в приближении транспаранта, составляющая электрического поля для бинарного аксикона будет иметь вид:

E y o ( r ) = ( 1 - e ^ф ) ^H) n circl ⁽ - I ,             (1)

n = 0             к rn J где rn=(n+1)r0, n – целое число, rn – радиусы скачков бинарного рельефа аксикона вдоль радиальной координаты r, φ – задержка фазы, к которой приводят выступ ы рельефа аксикона по отношению к впадинам рельефа, N – число скачков рельефа аксикона. Амплитуда спектра плоских волн для начального поля (1) находится из выражения:

k 2          N -1      ”      ( r ^

^ ( P ) = — ( 1 ^- e i ) E ^{( - 1)} n f ^cicrl I   I J 0⁽ kr P ) ^r dr =

^{2 П}          n =0      0       к r n J

N -1

= ( 1 - e ’ ) k ² г ^ ( - 1) ⁿ ( n + 1) 2 n =0

J 1 [ ^k P ^{( n + 1) r}0 ] [ k p ( n + 1) Г о ]

где ρ – безразмерная переменная.

Тогда амплитуду y -ой составляющей электрического поля на любой плоскости z найдем из выражения:

N -1

E y ( r , z ) = ( 1 - e ^ф ) k ² Г о² 5 ( - 1) n ( n + 1) 2

n =0

J J 1 [ kr o ( n + 1) p ] J [ ^kr o⁽ n ^{+ 1)} p ]

J ₀ ( k p r ) ek^^{1 p} p d p .

Задача нахождения амплитуды светового поля вблизи бинарного аксикона (3) свелась к вычислению интеграла:

J

I = J J 1 ( a x ) J ₀ ( p x ) e ^Y ^-x d x ,

где α, β, γ – постоянные числа. Интеграл (4) не удалось найти в справочной литературе, поэтому будем вычислять его в предельных случаях. Пусть γ = kz << 1 – мы хотим найти поле вблизи аксикона. Тогда, раскладывая в ряд Тейлора экспоненту, вместо (4) получим, сохранив только два члена ряда:

J

I - J J 1 ( a x ) J о ( в x ) d x +

j

+ i y J V1 - x²J 1 ( a x ) J ₀ ( в x )d x .

Первый интеграл можно найти в справочнике [11]:

J                    I 1Д, a > p,

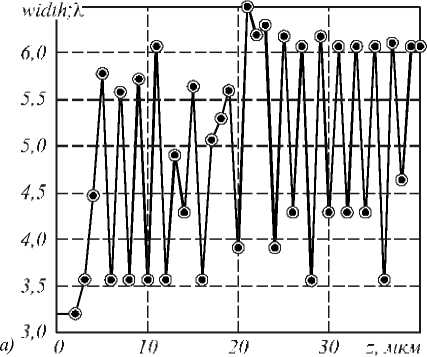
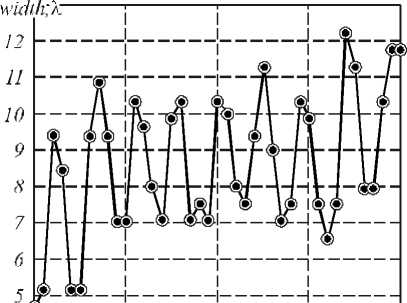
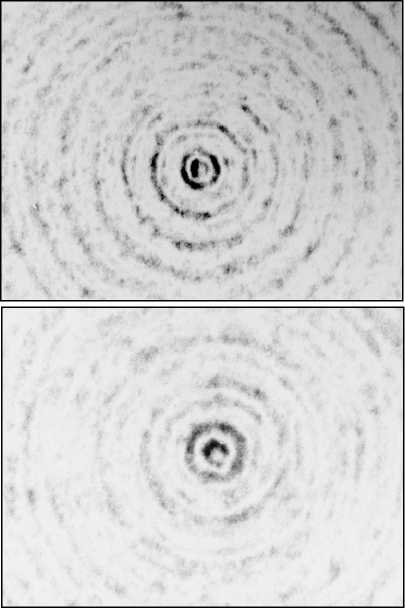
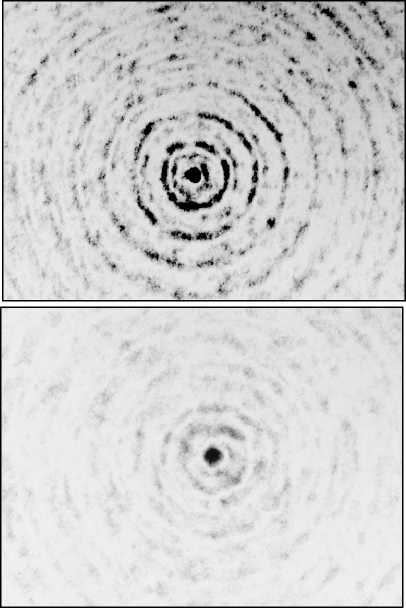
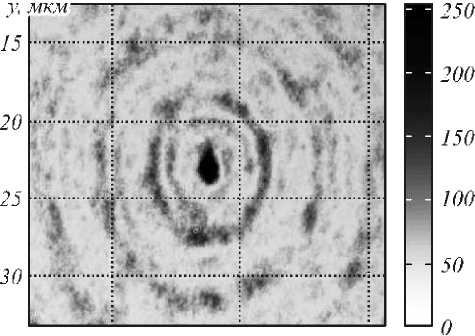
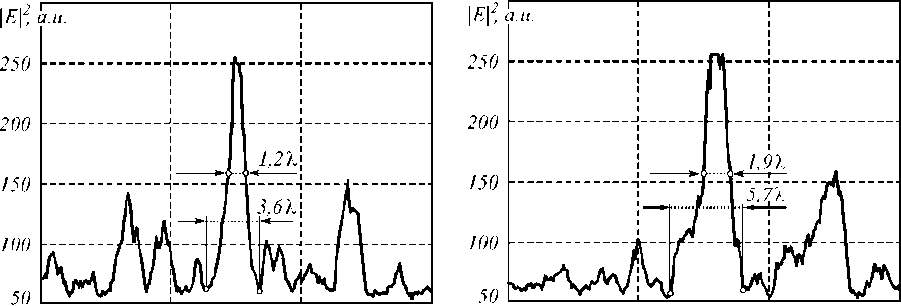
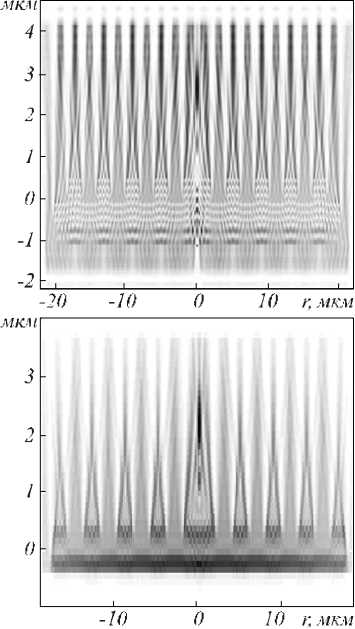
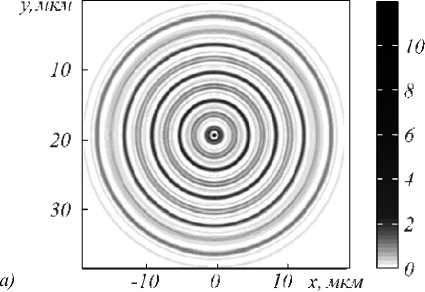
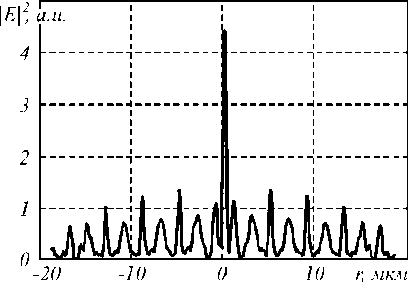
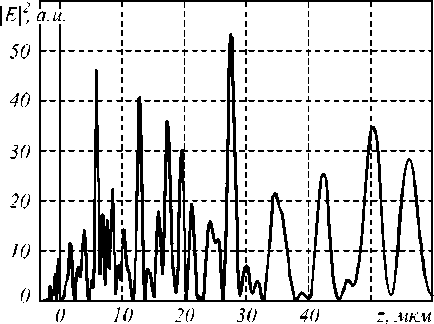
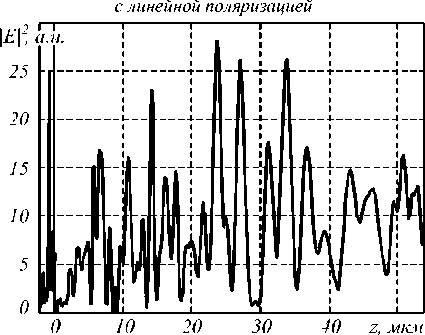
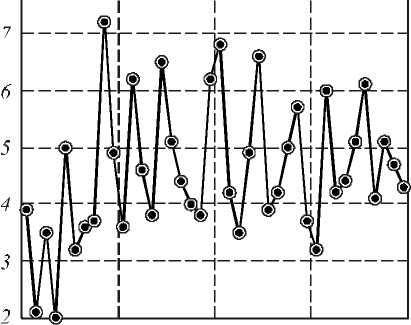
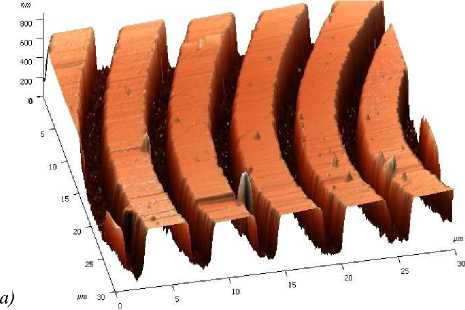
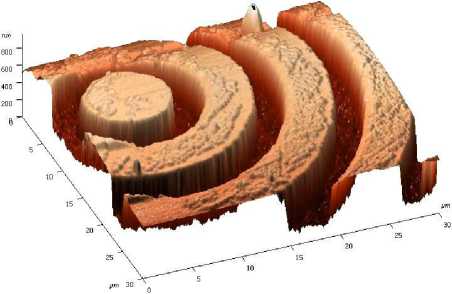
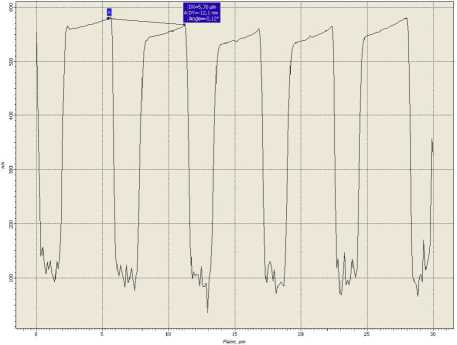
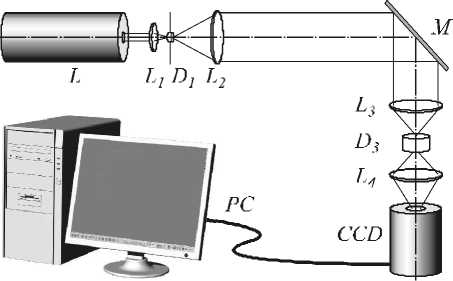
J J 1 ( a x ) J ₀ ( P x ) d x = < '^a о                   [ 0, a

.

В нашем сл учае: α = kr0 (n+1), β = kr. Второй интеграл в (5) найдем вблизи оптической оси, предположив, что радиальная координата r много меньше радиуса первого скачка рельефа аксикона r0: r<< r0, тогда функцию Бесселя нулевого порядка можно за-

, , . . fx У менить ее квадратной зависимостью: J0(x) -1 -1 — I при x << 1. Тогда для вычисления второго интеграла в (5) можно использовать справочный интеграл [11]:

J xa^-1(1 - x²) ^b-1Jn (cx )d x = 0

Чтобы проверить выражение (11), оценим диаметр центрального максимума интенсивности поля из други х соображений.

1.1. Параксиальная оценка диаметра осевого пучка

В [10] на основе скалярной параксиальной теории показано, что так как аксикон формирует пучок Бесселя, то диаметр пучка Бесселя можно оценить из выражения:

cn            I 2 J_x

²n⁺¹г fb+'J r( n+1)

I 2 J

J₀²(k sin 6- r) = 0 .

Тогда получим

„ n + a n + a ,    _ x F, -----,--+ b, n +1,

^{1 2}2 , 2         ’       ’

-

4 ,

2.4% n sin 6

где ₁F₂(a, b, c, x) – гипергеометрическая функция.

Тогда для второго интеграла в (5) можно записать выражение:

J V1- x²Ji(ox)dx -

- x²J1 (ax) dx =

-

kr H F I 1 - 1 1F2 I 1,^,1, 6 JI I 2

-

y²

-

(krL F ^f 2 — 2

, ,,

10 ^{1 2}1 2

-

y²lr,

kr где y = ^20-.

Замена бесконечных пределов интегрирования в (5) на конечные пределы интегрирования в (8) является обычной в таки х случаях процедурой, суть которой заключается в том, что пренебрегается вкладом в амплитуду затухающих неоднородных волн.

С учетом (6) и (8) получим для поля вблизи оптической оси и вблизи аксикона (kz<< 1, r<< r0):

Ey (r, _Z) - 1- + ikz (kr⁰) 1F2 kr₀        6

1,⁵,2, 2

-

y²

-

-

kt Ff2

, ,,

10 ^{1 2}1 2

-

y²

.

Из (9) можно получить выражение для оценки диаметра центрального максимума светового поля вблизи оптической оси:

2 r = k^-1

101F2 f1,|,2, - У² ,F2 ^f2,_?²,^-У²J

,

из которого можно получить числовую оценку диаметра фокуса:

2r - 0,6% .

Из (11) следует, что диаметр центрального максимума светового поля вблизи аксикона не зависит от его периода T = 2r0 и почти равен дифракционному пределу (FWHM = 0,51λ).

где θ – половина угла при вершине конической волны, которую формирует аксикон.

Для бинарного аксикона, рассматривая его как дифракционную ре шетку [9], можно считать, что угол θ конической волны в то же время является углом дифракционной решетки с периодом T:

%^m

Sin 6_m = — ,                             (14)

где m – номер порядка дифракции.

С учетом (13) и (14) получим окончательные выражения для оценки диаметра светового поля акси-кона на оптической оси:

2.4 TT

2 r = -,--- 0,774 — .(15)

n mm

Из (15) видно, что для бинарного аксикона диаметр Бесселева пучка не зависит от длины волны [10], а определяется только периодом аксикона и номером дифракционного порядка. Из (15) следует, что так как в точку на оптической оси вблизи аксикона будут приходить разные порядки дифракции от разных точек аксикона, то вблизи аксикона при z< z₀, где z₀=( R—/2%) - расстояние, после которого световое поле формирует только один порядок дифракции ак-сикона, R – радиус аксикона, будет формироваться световое поле, диаметр которого на оптической оси будет сложным образом меняться при 0 < z< z0.

Из (15) следует, что при z ≥ z0 диаметр осевого пучка будет равен 2r = 6,2λ для аксикона с периодом T = 4 мкм = 8λ.

1.2. Оценка диаметра осевого пучка как моды волновода

T

Вблизи аксикона при r< r₀ = — и z< — диаметр светового поля на оптической оси можно оценить из теории волноводов, так как глубина рельефа акси-кона H = —-—=% при n = 1,5 - показатель пре-2( n-1)

ломления, а центральную часть аксикона можно рассматривать как участок круглого волокна с радиусом сердечника равным r0 = T/2.

Число мод круглого волокна со ст упенчатым по-

казателем преломления рассчитывается на основе дисперсионного уравнения [12]:

uJ₀(u)wI₀ (w) ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^g              ^^^^^^* ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^_

J₁(u)       I₁(w)

где J0, J1, I0, I1 – обычные и модифицированные функции Бесселя нулевых и первых порядков, и² + w² = V², V = kr₀ ^n2 - n2 , где n₁и n₂- показатели

мое, то результат такой многолучевой интерференции предсказать будет трудно. Единственное, что можно сказать, это то, что при z<< R уравнение (19) сводится к уравнению (18), а из последнего следует, что вблизи поверхности аксикона минимальный период колебаний осевой интенсивности равен λ.

преломления сердечника и оболочки волокна,

r0 - его радиус.

Максимальный корень уравнения (16) для моды меньше числа отсечки umax<V, поэтому мода волновода с минимальным диаметром имеет амплитуду пропорциональную функции Бесселя: J0 (Vr)r₀),

r< r0. Тогда диаметр моды с максимальным номером будет равен (n = 1,5):

2 r = 2

2,4r0 V

2,4% пn2 -1

= 0,7%

Интересно, что оценка диаметра (17) также не зависит от периода аксикона T, как и оценка (11).

1.3. Непараксиальные выражения для осевой интенсивности

Зависимость диаметра центрального максимума светового поля от расстояния до аксикона должна коррелировать с зависимостью осевой интенсивности от расстояния до аксикона. Действительно, если на оси имеет место световое кольцо, то диаметр его больше по сравнению с диаметром в фокусе, а осевая интенсивность, наоборот, в случае фокуса достигает локального максимума, а в случае кольца – минимума. Поэтому получим выражение для осевой интенсивности света для бинарного аксикона. Известно выражение для осевой амплитуды скалярного непараксиального поля от круглого отверстия радиуса R в зависимости от продольной координаты [13]:

ik^R² + z^{2 z}

Ey (z) = ek - . . (18) V R² + z²

Для бинарного аксикона с пропусканием (1) можно аналогично найти выражение для амплитуды электрического вектора на оптической оси:

Были изготовлены три бинарных дифракционных аксикона с периодом 4, 6 и 8 мкм и диаметром 4 мм. Для их изготовления на кварцевую подложку (толщиной 1 мм, диаметром 30 мм) с показателем преломления n = 1,46 был напылён слой хрома толщиной 100 нм с помощью установки УВМ2М1. На такой пластинке с хромом записывался фотошаблон на круговой лазерной записывающей системе CLWS–200 с минимальным диаметром лазерного пятна 0,8 мкм и точностью позиционирования 20 нм. Запись фотошаблона представляла собой создание защитной оксидной пленки на поверхности хрома путем ее засвечивания сфокусированным пучком аргонового лазера с длиной волны 500 нм. После этого фото шаблон подвергался плазмохимическому травлению. Процесс травления осуществлялся на установке УТП ПДЭ-125-009, позволяющей получить детали рельефа, горизонтальный размер которых не менее 100 нм. Параметры травления кварца: мощность тока высокой частоты 800 Вт, предварительный вакуум 2,1×10^-2Па, ток электромагнита, локализующего плазму, 0,8 А. Травление проводилось в атмосфере фреона-12 в течение 21 минуты. Скорость травления кварцевой подложки была равна 20-25 нм в минуту. Таким образом были изготовлены три аксикона диаметром по 4 мм каждый с периодами 4 мкм, 6 мкм и 8 мкм.

На рис. 1 показан вид сверху бинарного аксикона на кварце с периодом 4 мкм, полученный с помощью растрового электронного микроскопа SUPRA-25-30-85 с увеличением в 1000 раз. На рис. 2 также вид сверху, но бинарного аксикона с периодом 8 мкм, полученный с помощью микроскопа на атомных силах Solver Pro.

Ey (z) = ei'

^ik^r2 N+1 ⁺z² ikz ze

e —i      =

.      V r2 N+1 ^{+ z}

2N

+ (e*-1) zZ m =1

ik r² + z²

m e— (-i)m r„2 + z z

,

где rm = mr0 – радиус скачка рельефа бинарного ак-сикона, r0= T/2 – половина периода аксикона.

Из (19) следует, что при ф = п в любую точку на оси z будут делать вклад сферические волны, исходящие как от вторичных источников от каждой точки скачков рельефа (то есть через полпериода акси-кона). Поскольку таких точек будет 2N + 1 слагае-

Рис. 1. Вид сверху бинарного аксикона с периодом 4мкм, полученный на растровом электронном микроскопе “Supra-25-30-85” с увеличением 1000

На рис. 3 показаны картины рельефа бинарных аксиконов, снятых с помощью микроскопа Solver

Pro под углом: периферийная часть аксикона с периодом 6 мкм (а) и центральная часть аксикона с периодом 8 мкм (б).

Рис. 2. Вид сверху бинарного аксикона с периодом 8мкм, полученный с помощью микроскопа на атомных силах Solver Pro

б)

Рис. 3. Вид под углом периферийной части бинарного аксикона с периодом 6 мкм (а) и центральной части аксикона с периодом 8 мкм (б), полученный с помощью микроскопа Solver Pro

На рис. 4 показано радиальное сечение периферийной части рельефа бинарного аксикона с периодом 6 мкм (рис. 3а), из которого видно, что глубина рельефа составляет 450-500 нм. Все три аксикона рассчитывались для длины волны 532 нм, поэтому расчетная глубина рельефа должна быть h = λ ≈ 578 нм.                       (20)

2(n-1)

Рис. 4. Сечение (профиль) рельефа бинарного аксикона с периодом 6 мкм, показанного на рис. 3а, полученное с помощью микроскопа Solver Pro

Поэтому о шибка в высоте травления рельефа (недотрав) составляет около 20%. Из рис. 4 также видно, что верхние грани рельефа имеют наклон около 1/150 радиана, на дне рельефа видны шероховатости с амплитудой 30 нм. Также имеет место трапецевидность бинарного рельефа: отношение длины «верха» ступеньки к длине «низа» ступеньки составляет 3:4. Кроме того, на рис. 2 хорошо заметно, что ширина ступеньки больше расстояния между соседними ступеньками (соотношение составляет приблизительно 2:1).

• 3.    Экспериментальные результаты

Целью эксперимента было исследование величины диаметра центрального пятна в зависимости от расстояния вдоль оптической оси. Изготовленные бинарные аксиконы помещались поочередно в оптическую схему на рис. 5, и с помощью ПЗС камеры измерялись картины дифракции в ближней зоне на разных расстояниях при освещении аксиконов коллимированным лазерным светом с длиной волны 532 нм.

Луч твердотельного лазера λ = 532 нм диаметром 1,4 мм фокусировался микрообъективом L1 в точечную диафрагму диаметром 15 мкм. После прохождения этой диафрагмы формировалось ровное световое пятно, центральная часть которого коллимировалась линзой L2. Сформированный пучок представлял собой почти плоскую волну с ограниченной апертурой. Центральная часть этого пучка вводилась в оптическую систему микроскопа Биолам-М, где фокусировалась микрообъективом L3 таким образом, чтобы диаметр лазерного пучка был равен диаметру акси-кона D3 (согласование диаметров светового пучка и аксикона выполнялось с целью уменьшения энергетических потерь). Получившаяся картина дифракции фиксировалась на CCD камеру через микрообъектив L4. При этом, смещая аксикон D3, можно было полу- чать картины дифракции на разных расстояниях от элемента. За точку отсчета принималась плоскость впадин микрорельефа. Эта плоскость определялась путем получения резкого изображения впадин микрорельефа в белом свете. Аксикон D3 смещался микрометрическим винтом с ценой деления 1 мкм. Разрешение CCD камеры составляло 2048×1536 пикселей с размером пикселя 6,9 мкм.

Рис. 5. Оптическая схема измерения картины дифракции в ближней зоне для бинарных аксиконов: L - лазер, L1 – микрообъектив (20×, NA = 0,4), D1 – точечная диафрагма (диаметр=15 мкм), L2 – коллимирующая линза (f = 100мм), M – поворотное зеркало, L3 – фокусирующий микрообъектив (8×, NA = 0,2), L4 – изображающий микрообъектив (20×, NA = 0,4), D3 – бинарный аксикон

На рис. 6 показано распределение диаметра центрального максимума (по одной из поперечных декартовых координат) от расстояния до поверхности аксиконов с периодом 4 мкм (а) и 8 мкм (б).

Из рис. 6 следует, что на расстоянии от 0 до 40 мкм диаметр центрального максимума интенсивности меняется квазипериодически с примерным периодом колебаний 2 мкм (рис. 6а) и 4 мкм (рис. 6б). Причем значения диаметров больше 5λ (рис. 6а) и 9λ (рис. 6б) соответствуют диаметру кольцевого распределения интенсивности на оси (т.е. в этом случае интенсивность на оси имеет локальный минимум), а значения диаметров меньше 4,5λ (рис. 6а) и 8λ (рис. 6б) соответствуют диамет- рам локальных максимумов (фокальных точек). Анализ рис. 6 позволяет заключить, что диаметр осевых фокальных пятен в ближней зоне (на расстоянии до 40 мкм) меняется от 3,5λ до 4,5λ (рис. 6а) с ошибкой 0,4λ и от 5λ до 8λ (рис. 6б) – с о шибкой 0,5λ, соответственно для аксиконов с периодом 4 мкм и 8 мкм.

На рис. 7 показаны зарегистрированные картины дифракции лазерного света на бинарных аксиконах с периодом 4 мкм (а, б) и 8 мкм (в, г) на расстояниях 5 мкм (а), 8 мкм (б), 16 мкм (в) и 18 мкм (г). Из рис. 7 видно, что кольцевое распределение интенсивности на оптической оси (а, в) сменяется формированием фокального пятна (центрального максимума) через 2-3 мкм на расстояниях, меньших 40 мкм. Масштаб картин дифракции на рис. 7 одинаковый (75×55 мкм), поэтому можно видеть, что диаметры кольца и фокуса для аксикона с периодом 8 мкм в 1,5 раза боль ше, чем для аксикона с периодом 4 мкм.

На рис. 8 показана картина дифракции на акси-коне с периодом 4 мкм, зарегистрированная на расстоянии 2 мкм от его поверхности (а), и ее сечения по осям x (б) и y (в). Из рис. 8 можно видеть, что при небольших расстояниях z<5 мкм (на рис. 7 эллиптичность уже не обнаруживается) в картине дифракции можно наблюдать эллиптичность фокального пятна (эксцентриситет ε = 0,63), связанную с линейной поляризацией падающего на аксикон лазерного света (электрический вектор падающего пучка направлен вдоль оси y на рис. 8).

• 4.    Результаты моделирования

Моделирование дифракции линейно-поляризованной плоской волны на бинарных дифракционных аксиконах проводилось двумя близкими, но разными методами: методом R-FDTD, реализующим в среде Matlab алгоритм разностного решения системы уравнений Максвелла в цилиндрических координатах [14], и 3D-FDTD методом, реализованным в программе FullWAVE (фирма RSoft, США).

Рис. 6. Зависимость диаметра пятна интенсивности на оптической оси (в длинах волн) от расстояния до бинарных аксиконов с периодом 4 мкм (а) и 8 мкм (б)

4 I_____________________________I______________________________I_____________________________I______________________________

б)    0        10       20       30 z, mkai

Рис. 7. Зарегистрированные ПЗС камерой картины дифракции для аксиконов с периодом 4 мкм (а, б) и 8 мкм (в, г) на разных расстояниях: 5 мкм (а), 8 мкм(б), 16 мкм(в) и 18 мкм(г)

а)           20           30 х, Л1км

• б)    20          25           30 х, мкм в)    15          20           25 у, мкм

Рис. 8. Распределение интенсивности, зарегистрированное на расстоянии 2 мкм от бинарного аксикона с периодом 4 мкм (а), и его сечения по осям x (б) и y (в)

На рис. 9 показаны распределения квадрата модуля электрического вектора в плоскости XZ линейно-поляризованной плоской волны, прошедшей бинарный аксикон с периодом 4 мкм, рассчитанные двумя разными методами. Из рис. 9 видно, что качественно обе картины дифракции согласуются, так как на обеих картинах видно, что каждый выступ рельефа аксикона фокусирует свет в локальные фокусы на расстоянии 2 мкм (рис. 9а) и 1,7 мкм (рис. 9б) от поверхности аксикона. Эти значения согласуются с оценкой, которая следует из (18). Из (18) в параксиальном случае следует, что интенсивность вдоль оптической оси будет меняться пропорционально cos (kR2/4z) с периодом z₀= R²/4λ = 1,9 мкм при T = 4 мкм.

На рис. 10 показаны картины дифракции в плоскости XY на расстоянии z = 1,7 мкм (в плоскости локального фокуса) (а) и ее радиальное сечение (б); для сравнения показано распределение интенсивности в плоскости XY на расстоянии z = 0,3 мкм (в), где на оптической оси формируется световое кольцо.

Из рис. 10а, б можно оценить диаметр локального максимума, который равен 1,25 λ (λ = 532 нм). Если сравнить это значение с диаметром экспериментально зарегистрированного локального фокусного пятна на рис. 8 (диаметр по оси x равен 3,6 λ), то оно окажется почти в 3 раза меньше.

а)

б)

Рис. 9. Рассчитанное распределение интенсивности в плоскости XZ при дифракции линейно-поляризованной плоской волны (электрический вектор направлен вдоль оси Y) на бинарном аксиконе с периодом 4 мкм: Matlab2008a (а) FullWAVE (RSoft) (б)

Рис. 10. Рассчитанное с помощью программы FullWAVE (RSoft) распределение интенсивности в поперечной плоскости XY на расстоянии 1,7 мкм (а) и его сечение (б) и на расстоянии 0,3 мкм (в) для бинарного аксикона с периодом 4 мкм

На рис. 11 показано рассчитанное с помощь ю R-FDTD метода осевое распределение интенсивности для аксикона радиусом 28 мкм и с периодом 4 мкм, освещенного плоской волной с линейной поляризацией.

Из рис. 11 следует, что локальные экстремумы вдоль оптической оси сменяют друг друга квазипе-риодическим образом. Расстояние между соседними максимумами растет от 2 мкм до 8 мкм на расстоянии z< 60 мкм.

На рис. 12 показано распределение интенсивности света (в произвольных единицах) вдоль оптической оси для бинарного аксикона с периодом 4 мкм и радиусом 28 мкм. В отличие от рис. 11 в данном случае (рис. 12) аксикон освещался расходящимся гауссовым пучком с линейной поляризацией с амплитудой электрического вектора в виде:

f r²    kr²)

Ey (r, z = 0) = exP I^-2 + i— I, V w    ² f )

где w = 2 мм – ра ди ус перетяжки гаус со ва п учка, f = 2,5 w – фокусное расстояние параболической линзы.

Рис. 11. Рассчитанное с помощью R-FDTD метода осевое распределение интенсивности для аксикона с периодом 4 мкм, освещаемого плоской волной

Рис. 12. Распределение интенсивности вдоль оптической оси, рассчитанное с помощью R-FDTD метода для аксикона с периодом 4 мкм, радиус аксикона – 28 мкм, освещаемого расходящимся гауссовым пучком с линейной поляризацией

Расходящийся пучок (в отличие от плоского, который исследовался до сих пор) был использован, чтобы лучше согласовать расчеты с экспериментальными результатами, полученными по схеме на рис. 5. В схеме на рис. 5 бинарный аксикон D₃ с диаметром 4 мм освещался расходящимся лазерным светом после микрообъектива L3. Расходящийся пучок света был использован, чтобы согласовать диаметр освещаю щего с ветового пятна с диаметром аксикона D3. На рис. 12 расстояние между соседними максимумами интенсивности растет с 2 мкм до 4 мкм при z< 50 мкм. Из сравнения рис. 11 и 12 ви дно, что при 0 < z< 30 мкм период колебаний интенси вно сти п риме рно одинаков, а в области 30 < z< 50 микрон период колебаний интенсивности на рис. 12 меньше.

На рис. 13 показаны рассчитанные R-FDTD методом диаметры центральных пятен картины ди- фракции расходящейся волны (20) на аксиконе с периодом T = 4 мкм в зависимости от расстояния до аксикона.

На рис. 13 локальные максимумы соответствуют кольцевому распределению интенсивности в центральном пятне картины дифракции, а локальные минимумы – фокальным пятнам на оптической оси.

Из рис. 13 также видно, что диаметр фокальных пятен на оптической оси для бинарного аксикона с периодом 4 мкм в ближней зоне (z< 40 мкм) меняется в пределах от 2λ до 4,3λ с продольным периодом примерно 3 мкм (на 40 мкм имеется 12 локальных минимумов на рис. 13). Из сравнения экспериментальной кривой диаметров центральных пятен картин дифракции (рис. 6а) с расчетной кривой диаметров центральных пятен (рис. 13) следует, что имеет место согласование по диаметру фокальных пятен на расстоянии до 40 мкм: от 3,5λ до 4,5λ (рис. 6а) и от 2λ до 4,3λ (рис. 13). Хотя продольный период изменения диаметра фокальных пятен на рис. 13 составил 3 мкм, а в эксперименте был 2 мкм.

width',7~

0        10       20       30 z, лиси

Рис. 13. Рассчитанное с помощью R-FDTD метода распределение полной ширины (диаметр вдоль оси x в длинах волн) центрального макисмума интенсивности в картине дифракции расходящегося лазерного пучка на бинарном аксиконе с периодом 4 мкм

Из сравнения рис. 12 и 13 видно, что имеет место согласование числа локальных фокусов (минимум на рис. 13) и локальных максимумов интенсивности (рис. 12): в промежутке между 30 мкм < z<40 мкм на рис. 13 имеется 4 минимума, а на рис. 12 – 4 максимума; в промежутке между 20 мкм < z<30 мкм на рис. 13 всего 2 минимума, а на рис. 12 – два больших максимума.

Из уравнения (15) следует, что диаметр фокального пятна для аксикона с периодом 4 мкм будет равен: 2r = 0,774T =3,1 мкм=6λ, при m = 1 и 3λ при m =2. Сравнивая эти числа с экспериментом (рис. 6а) и расчетом (рис. 13), можно заключить, что в ближней зоне дифракции вклад в формирование фокусов вдоль оптической оси делают первый и второй порядки дифракции бинарного аксикона.

Были получены следую щие рез ультаты:

– Показано, что расчет непараксиальной комплексной амплитуды светового поля дифракции плоской волны на бинарном аксиконе сводится к расчету интеграла от произведения двух функций Бесселя нулевого и первого порядков (уравнения (3), (4)).

– На основе приближенного вычисления при z<< λ показано, что диаметр центрального максимума светового поля не зависит от периода аксикона и равен дифракционному пределу 0,6 λ (ура внение (11)). Эта оценка диаметра фокального пятна вблизи поверхности аксикона согласуется с оценкой минимального диаметра модуляции светового поля (0,7λ), состоящего из пространственных мод ступенчатого волновода, диаметр которого равен периоду аксикона (уравнение (17)).

– Получено выражение для комплексной амплитуды на оптической оси светового поля при дифракции плоской волны на бинарном аксиконе (уравнение (19)), из которого следует, что вблизи поверхности аксикона минимальный период колебаний осевой интенсивности равен λ.

– С помощью лазерной записывающей системы CLWS-200 и плазмохимического травления были изготовлены на кварце (n = 1,46) бинарные аксиконы с периодом 4 мкм, 6 мкм и 8 мкм, диаметром 4 мм и глубиной 500 нм. Анализ поверхности аксиконов с помощью микроскопа Solver Pro показал, что глубина рельефа аксикона отличается от проектной на 20%. Верхние грани рельефа имеют наклон около 0,01 радиана, ступеньки бинарного рельефа имеют трапецевидность 3:4, и на дне рельефа имеется шероховатость с амплитудой 30 нм.

– Получены экспериментальные зависимости изменения диаметра фокальных пятен вдоль оптической оси в ближней зоне бинарных аксиконов (z<40 мкм) и показано, что для аксикона с периодом 4 мкм диаметр фокальных пятен меняется от 3,5λ до 4,5λ с периодом 2 мкм, а для аксикона с периодом 8 мкм – от 5λ до 8λ с периодом 4 мкм (рис. 6).

– Минимальный диаметр эллиптического фокального пятна был равен 3,6λ мкм (FWHM = 1,2 λ) на расстоянии 2 мкм от аксикона с периодом 4 мкм (рис. 8). Этот согласуется в работами [2,6].

– Экспериментально показано, что на небольши х расстояниях от поверхности аксикона (z<5 мкм) наблюдается эллиптичность фокальных пятен (эксцентриситет эллипса 0,63), которые вытянуты вдоль вектора линейной поляризации падающей на акси-кон световой волны.

– Проведено сравнительное моделирование дифракции плоской линейно-поляризованной волны на бинарном аксиконе с периодом 4 мкм и диаметром 40 мкм с помощью программы FullWAVE (фирма RSoft), реализующей 3D-FDTD метод решения уравнений Максвелла в декартовых координатах, и с помощью разработанной ранее программы R-FDTD, реализующей разностный метод решения уравнений Максвелла в цилиндрической системе координат для элементов микрооптики с радиальной симметрией. Обе рассчитанные картины дифракции показывают, что первый фокус для аксикона появляется на расстоянии около 1,7-2 мкм от его поверхности (рис. 9).

– Показано, что расчетная зависимость изменения диаметра центрального пятна картины дифракции расходящейся линейно-поляризованной волны на бинарном аксиконе с периодом 4 мкм согласуется с аналогичной экспериментальной кривой (рис. 6а и 13): на расстоянии 0< z<40 мкм диаметр фокальных пятен на оптической оси лежит в диапазоне от 3,5λ до 4,5λ (эксперимент) и от 2λ до 4,3λ (расчет), при этом локальные фокусы на оси появляются через 2 мкм (эксперимент) и 3 мкм (расчет).

Работа выполнена при поддержке грантов Президента РФ НШ-7414.2010.9 и МД-8026.2010.2.