Дифференциации работников по заработной плате: методология ранжирования на примере регионов России

Актуальность

Различные аспекты проблем, связанных с неравенством распределения доходов, рассматриваются в работах Аткинсона А.Б. и Бургиньона Ф. (2000), Айвазяна С. А. (2012), Кобхэма А. и Самнера А. (2013), Клейбера С. и Коца С. (2003), Кузнеца С. (1955), Лившица В. Н. (2018), Пальмы (2006), Шевякова А. и Кируты А. (2009), Стиглица Дж. (2012) и других. Для количественной оценки расслоения населения по доходам используются различные показатели. Однако все эти показатели лишь частично характеризуют степень расслоения населения по доходам. Целью исследования является совершенствование методологии ранжирования регионов на основе использования некоторых новых показателей структурной дифференциации населения по доходам. Для проверки предложенного нами подхода мы использовали данные Федеральной службы государственной статистики о среднемесячной заработной плате в 10-процентных группах работников организаций в 85 субъектах Российской Федерации в апреле 2019 года (Росстат, 2020 год). Эта информация используется для построения функции Лоренца. Для расчета показателей структурной дифференциации используется подход, при котором все сотрудники исследуемых организаций, ранжированные по заработной плате, делятся на две или три группы. Рассматриваются подразделения сотрудников в пропорциях 40-50-10, 40-40-20, 50-50. В дополнение к традиционным критериям оценки дифференциации мы используем критерии, отражающие структурное неравенство, такие как соотношение средних значений некоторых двух групп сотрудников, разделенных на три группы в определенной пропорции.

Постановка задачи

Информация о распределении средств, выделяемых на оплату труда, по децильным группам работников 85 субъектов Российской Федерации приведена в табличной форме. Здесь у нас есть названия федеральных округов и субъектов Российской Федерации, а также ^ - значения средней заработной платы сотрудников к -го дециля ( к = 1, 2, ..., 10). Этой информации достаточно, чтобы получить представление о степени дифференциации работников в разных регионах страны по уровню заработной платы и выполнить ранжирование субъектов Российской Федерации по степени неравенства в распределении средств, выделяемых на оплату труда.

В дальнейшем для каждого конкретного региона (федерального округа, субъекта федерации и т.д.) Российской Федерации используются следующие обозначения:

D_k - к -тая децильная группа (дециль), к = 1, 2,..., 10;

том 17 № 4 (53), 2021, ст. 1

• y - совокупная доля сотрудников;

• z - совокупная доля средств, выделяемых на оплату труда, в децилях с первого по k, ( z_Y0 = 1);

• d - доля средств, полученных работниками k -го дециля;

• µ - средняя заработная плата сотрудников (тыс. руб.);

• x - заработная плата (тысячи рублей).

Для вывода формул расчета различных показателей дифференциации на основе статистических данных ( к , ц ) , где к = 1, 2,..., 10 используются функция распределения сотрудников по заработной плате у = F ( x ) и функция Лоренца z = L ( у ) . Эти функции связаны соотношением

• L‘(У) = НУ)/ Ц

где ф ( у ) - обратная функция функции распределения , у = F ( x ) , ц - средняя заработная плата работников конкретного региона.

Важно, чтобы L (0) = 0 , L (1) = 1 , поскольку

1 у1

• L(У) = - J Ф(t)dt, Ц = J ИУ)dy.

Ц 00

Предположение о том, что функция Лоренца кусочно-линейна, позволяет нам обосновать следующие приближенные формулы. Величина средней заработной платы: 1

• Ц=ТО §Цк'

Доля средств, полученных работниками к -го дециля ( к = 1,...,10 ), в общей сумме средств, выделенных на оплату труда:

dk = Цк /(10ц) .(4)

Значения табличной функции Лоренца { у₃ ; z_} }, где : z₅ = L ( у ,):

• У0 = 0, у, = j/10; z0 = 0, zy=fbdk; j = 1,...,10.

к =1

Значения µ и расчетные значения z функции Лоренца позволяют построить кусочно-линейную функцию Лоренца, а также рассчитать значения большинства показателей дифференциации населения по доходам, используемых на практике (рис. 1).

том 17 № 4 (53), 2021, ст. 1

На рисунке 1 показаны кривые Лоренца для Республики Тыва (линия 2), Ярославской области (линия 3) и Москвы (линия 4), построенные с использованием описанного алгоритма. Кривые Лоренца для других субъектов федерации расположены между строками 2 и 4, так как в Москве самый высокий коэффициент Джини (0,429), а в Республике Тыва — самый низкий (0,288).

Давайте выпишем формулы для расчета некоторых показателей дифференциации населения по доходам, которые используются на практике.

Децильные и квинтильные коэффициенты (децильные и квинтильные коэффициенты доли доходов):

KF = М 10 / M l ,   KF 2 = ( M s + М 10^)/( М 1 + М 2 ) .                                          (6)

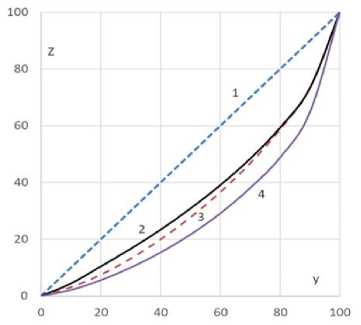
Рис. 1. Уравнительная линия (1) и кривые Лоренца для трех субъектов Российской Федерации: линия 2 - Республика Тыва, линия 3 - Ярославская область, линия 4 - Москва. Источник: расчеты авторов на основе данных Росстата за 2020 г.

Коэффициент Джини:

KG = 0,9 - 0,2 ]T z_j .                                                               (7)

j = 1

Индекс Пальмы:

KP = M io^/( M 1 + М 2 + М з + М д ) .                                                       ⁽⁸⁾

Коэффициенты (6) и (8) могут быть выражены с помощью функции таблицы Лоренца:

KF = (1 - z 9 )/ z i , KF ^ = (1 - z ₈ )/ z 2 , KP = (1 - z 9 )/ z ₄.

Рейтинг регионов России по степени дифференциации работников по заработной плате

На рисунке 2 показаны три набора точек { IG ; KF_X V} { IG_} ; KF ₂2_у } и { IG_} ; Kp } на

IG - U плоскости для 85 субъектов федерации (j = 1,2,...,85), описывающие взаимосвязь www.rypravlenie.ru

том 17 № 4 (53), 2021, ст. 1

между индексом Джини IGj = 100 • KGj , децильным и квинтильным коэффициентами (6) и индексом Пальмы (8). Эти точки сгруппированы рядом с линиями 1, 2 и 3 соответственно.

Как вы можете видеть, для подавляющего большинства субъектов индекс Джини ниже 35. Восемь субъектов федерации имеют больше этого значения: Москва - 42,9, Сахалинская область - 39,3, Астраханская область - 37,7, Тюменская область (кроме Ханты-Мансийского автономного округа–Югры и Ямало-Ненецкого автономного округа) - 37,4, Красноярский край - 36,7, Санкт-Петербург - 37,0, Московская область - 36,1 и Магаданская область - 35,2.

Давайте предположим, что  KFn  это соотношение средних доходов двух противоположных групп населения: нижняя состоит из m децилей D + D2 +... + Dm, а верхняя из n децилей D10 + D9 + ...+ Dn п . Итак, если m = n = 1 или m = n = 2 и тогда у нас есть уравнения (6). Следовательно, коэффициент KFn является обобщением децильных и квинтильных коэффициентов. Давайте напишем формулу для расчета обобщенного коэффициента дифференцирования:

KF m ⁿ

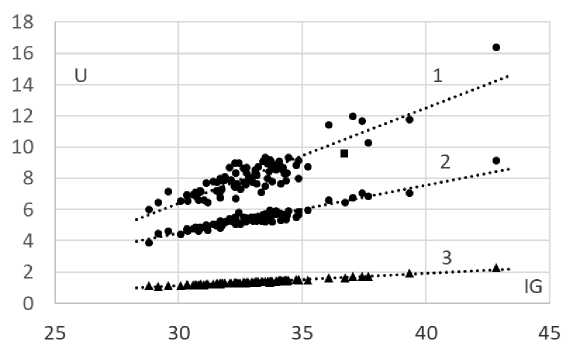
Рис. 2. Корреляция децильного коэффициента, квинтильного коэффициента и индекса Пальмы с коэффициентом Джини для 85 субъектов Российской Федерации (соответствующие точки сгруппированы вблизи линий 1, 2 и 3 на плоскости соответственно).

Источник: расчеты авторов на основе данных Росстата за 2020 г.

m ¹ - z 10 - n

n

m

Если m = 4, n = 1 , то KF 1 = 4 • (1 - z ₉) / z ₄ = 4 • KP .

Таким образом, коэффициент Пальмы в четыре раза меньше, чем соотношение средних доходов двух противоположных групп (нижняя состоит из четырех децилей D + D ₂ + D ₃ + D ₄, а верхняя - из одного дециля D_{x 0}).

На рисунке 3 точки { IG ; z₄ .} , { IG ;( z ₉ - z ₄) .} и { IG ; (1 - z ₉).} нанесены для 85 субъектов федерации ( j = 1, 2,...,85), описание распределения заработной платы по группам, разделенным в пропорции 40-50-10. Эти точки сгруппированы рядом с линиями 1, 2 и 3 соответственно. Как видите, доля средств, получаемых сотрудниками первой группы (1-4 дециля), составляет около 20% для большинства субъектов, и эта доля уменьшается с ростом коэффициента Джини. Доля средств, полученных работниками второй группы (5-9 децилей), находится в диапазоне от 48% до 56%. Из этого следует, что гипотеза Пальмы о распределении работников по заработной плате выполняется не во всех субъектах Российской Федерации. Напомним, что согласно гипотезе Пальмы, «население в децилях 5-9 удерживает относительно стабильную половину валового национального дохода» (Кобхэм А. и Самнер А., 2013; Пальма, 2013). В то же время доля средств, получаемых работниками десятого дециля, увеличивается с ростом коэффициента Джини. Это означает, что увеличение неравенства в первую очередь связано с увеличением доли средств, получаемых работниками десятого дециля.

Подход, использованный Пальмой (2013) для разделения населения на три части (в частности, в пропорции 40-50-10), устраняет ограничения традиционного подхода, связанные с использованием децильных и квинтильных коэффициентов при анализе дифференциации населения по доходам.

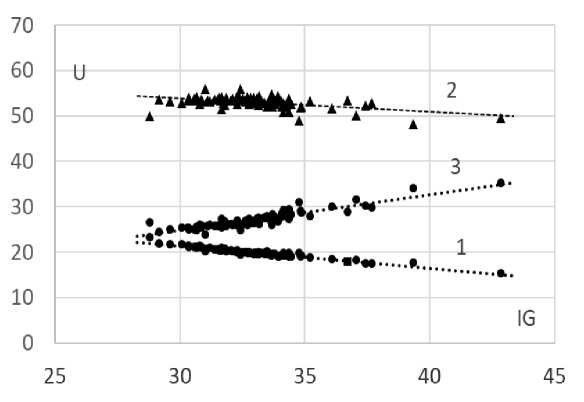
Рис. 3. Соотношение долей средств (в процентах), полученных сотрудниками первой, второй и третьей групп подразделения Palma 40-50-10, с коэффициентом Джини (соответствующие точки сгруппированы возле линий 1, 2 и 3 на плоскости соответственно).

Источник: расчеты авторов на основе данных Росстата за 2020 г.

Например, при использовании квинтильного коэффициента мы можем говорить о разделении населения в пропорции 20-60-20. В этой связи отметим, что разделение населения по доходам на три группы уже давно используется на практике. Так, в Отчете о глобальной заработной плате (2015 г.) при выполнении оценок неравенства между

«верхним» и «нижним» децилями, а также внутри «среднего класса» население фактически разделено на три группы в пропорции 30-40-30. В этом случае неравенство среднего класса измеряется как соотношение ^ (0.7) / ^ (0.3) . Это предполагает заданную функцию распределения населения по доходам.

В таблице 1 приведена средняя заработная плата различных групп работников в федеральных округах Российской Федерации. В частности, в третьем столбце показаны значения средней заработной платы в целом по округу; в четвертом, пятом и шестом столбцах содержатся значения средней заработной платы в трех группах с разделением на 40-50-10 соответственно; седьмое и восьмое значения заработной платы в нижней и верхней половинах работников; в девятом столбце значения заработной платы в группах по четыре дециля.

Таблица 1. Средняя заработная плата различных групп работников в федеральных округах

Российской Федерации (тыс. руб.)

	М	4 M i	9 M 5	M 10	M 1	10 М б	M 8
1                     2	3	4	5	6	7	8	9
Российская Федерация	47.7	19.7	48.1	157.2	22.1	73.2	42.1
Федеральный округ
1    Центральный	59.7	21.7	57.6	222.8	24.6	94.8	49.9
2    Северо-Западный	55.4	24.9	57.7	166.5	27.9	83.0	51.4
3   Южный	34.1	16.6	36.2	93.7	18.5	49.7	32.6
4    Северокавказский	27.5	13.6	29.0	75.2	14.9	40.0	25.9
5   Приволжский	35.3	17.3	37.3	97.0	19.2	51.3	33.6
6    Уральский	52.2	22.6	54.7	158.4	25.3	79.1	47.9
7    Сибирский	41.7	19.6	44.0	118.8	21.7	61.8	39.1
8    Дальневосточный	57.2	25.9	60.4	166.6	29.0	85.5	53.8
Источник: расчеты авторов на основе данных Росстата за 2020 г.

Для сравнения значений средней заработной платы в двух группах работников мы предлагаем использовать следующий структурный показатель дифференциации:

М ⁹

_Sp ^{- 9}       .                                                                                          (11)

m - n      n

M m

Здесь первая группа работников состоит из децилей Dm + Dm+х+... + Dn, а вторая группа состоит из децилей  Dp + Dp+,+... + D.. Использование этого показателя одновременно с традиционными показателями позволяет получить дополнительную информацию о расслоении населения по доходам.

Таблица 2. Индикаторы дифференциации работников федеральных округов РФ по заработной плате

		KF 1	KF 2	IG	KF 4 1	5 - 9 S 1 - 4	S 16 -- 510	5 - 8 S 1 - 4
1	2	3	4	5	6	7	8	9
	Российская Федерация	13.0	7.7	40.0	8.0	2.4	3.3	2.1
Федеральный округ
1	Центральный	17.7	9.8	44.5	10.3	2.7	3.8	2.3
2	Уральский	11.8	7.2	38.0	7.0	2.4	3.1	2.1
3	Северо-Западный	11.0	6.6	36.7	6.7	2.3	3.0	2.1
4	Дальневосточный	10.1	6.4	36.1	6.4	2.3	3.0	2.1
5	Сибирский	9.1	5.9	35.1	6.1	2.2	2.8	2.0
6	Южный	8.7	5.7	33.6	5.7	2.2	2.7	2.0
7	Приволжский	8.6	5.5	33.4	5.6	2.1	2.7	1.9
8	Северокавказский	7.6	5.3	33.3	5.5	2.1	2.7	1.9

Источник: расчеты авторов на основе данных Росстата за 2020 г.

В то же время наибольшее расслоение работников по уровню заработной платы происходит в Центральном федеральном округе. Здесь индекс Джини составляет 44,5, а соотношение средней заработной платы в 10-м дециле более чем в 10 раз превышает среднюю заработную плату работников в первых четырех децилях (колонка 6). Если исключить из рассмотрения 20% сотрудников с самым высоким заработком, то заработная плата 80% остальных сотрудников распределяется более равномерно. Об этом свидетельствуют и показатели S ^{6 - 10} и S ^{5 - 8} . Например, показатель S ^{6 - 10} = 3,8 в Центральном федеральном округе. Это означает, что средняя заработная плата сотрудников, получающих зарплату выше и ниже медианы, отличается почти в 4 раза. В то же время разрыв между средней зарплатой 80% сотрудников (децили с первого по восьмой), деленной на медиану, ϕ (0.4) составляет S ^{5 - 8} = 2, 3 . Тот факт, что значение показателя S ^{5 - 8} не сильно отличается от 2 во всех округах, указывает на значительное влияние десятого дециля заработной платы работников на дифференциацию в распределении заработной платы.

Давайте теперь рассмотрим 18 субъектов федерации Центрального федерального округа, для которых характерно наибольшее расслоение работников. В таблице 3 приведены значения средней заработной платы различных групп работников этих субъектов, сгруппированные по аналогии с группировкой работников в таблице 1. Из таблицы видно, что, например, у половины москвичей средняя зарплата составляет 41,7 тысячи рублей (колонка 8), а у другой половины средняя зарплата составляет 150,4 тысячи рублей. С другой стороны, если мы возьмем 80% москвичей с более низкой зарплатой, то половина этого часть москвичей (децили 1, 2, 3 и 4) имеют среднюю зарплату 36,9 тысячи рублей (графа 4), а другая половина (децили 5, 6, 7 и 8) – 80,4 тысячи рублей. В то же время средняя зарплата www.rypravlenie.ru

том 17 № 4 (53), 2021, ст. 1

50% московских сотрудников (децили 5, 6, 7, 8 и 9) составляет 95 тысяч рублей, и это соответствует гипотезе Пальмы.

Таблица 3. Средняя заработная плата различных групп работников 18 субъектов федерации Центрального федерального округа (тыс. руб.)

	Субъекты федерации	µ	4 µ 1	9 µ 5	10 µ 5	µ 10	µ 1 5	9 µ 6
1	2	3	4	5	6	7	8	9
1	Белгородская область	35.0	19.1	37.3	45.7	87.4	20.9	39.6
2	Брянская область	30.0	15.0	32.3	40.0	78.2	16.6	34.7
3	Владимирская область	33.5	17.4	35.8	44.2	86.4	19.2	38.1
4	Воронежская область	34.9	17.4	36.9	46.6	95.1	19.2	39.5
5	Ивановская область	27.8	14.7	29.9	36.6	70.5	16.1	31.9
6	Калужская область	41.1	20.2	43.4	55.1	113.3	22.4	46.5
7	Костромская область	29.9	14.9	31.4	39.9	82.5	16.4	33.6
8	Курская область	32.0	16.9	34.2	42.1	81.4	18.5	36.5
9	Липецкая область	35.2	17.4	37.5	47.0	94.6	19.3	40.2
10	Московская область	56.7	26.0	58.6	77.2	170.1	29.3	62.7
11	Орловская область	27.8	14.9	29.7	36.5	70.4	16.2	31.6
12	Рязанская область	34.0	17.2	36.7	45.2	87.7	19.1	39.3
13	Смоленская область	32.4	15.9	35.0	43.4	85.5	17.7	37.4
14	Тамбовская область	29.1	15.3	31.1	38.2	74.2	16.9	33.1
15	Тверская область	33.8	16.1	36.7	45.7	90.4	18.0	39.5
16	Тульская область	38.5	19.6	40.5	51.1	104.1	21.7	43.2
17	Ярославская область	36.0	18.0	38.4	48.1	96.3	20.0	41.0
18	Москва	96.0	36.9	95.0	135.5	337.8	41.7	103.6

Источник: расчеты авторов на основе данных Росстата за 2020 г.

Значения структурных показателей дифференциации населения, приведенные в таблице 4, рассчитаны с использованием простого алгоритма построения табличной функции Лоренца на основе информации о распределении средств по 10-процентным (децильным) группам работников организаций. Эти значения структурных показателей свидетельствуют о том, что основной причиной дифференциации работников по заработной плате являются высокие значения доли доходов в девятой и, особенно, в десятой децильных группах.

Несмотря на ясность полученных результатов, используемый подход не позволяет решить задачу построения функции распределения сотрудников по заработной плате и соответствующей обратной функции и функции плотности распределения. По-видимому, один из подходов к углублению анализа численности населения дифференциация по доходу - это использование методов вычислительной математики (например, метода сплайновой аппроксимации), который позволяет решить не только эти задачи, но и построить функцию эластичности кривой Лоренца u = yL ′ ( y ) / y .

Заключение

Существующие показатели дифференциации населения по доходам (индексы

Кузнеца, Гувера, Пальмы и др.) лишь частично характеризуют степень расслоения населения по денежным доходам. В статье используется подход, при котором все сотрудники в регионе, ранжированные по заработной плате, делятся на две или три группы в пропорциях 50-50, 40-50-10, 40-40-20. Для построения функций Лоренца используется метод кусочнолинейной аппроксимации табличных данных. Установлено, что в субъектах Российской Федерации доля средств, получаемых средней группой работников, разделенных в пропорции 40-50-10, лежит в диапазоне от 48% до 56%. Таким образом, гипотеза Пальмы при рассмотрении распределения работников по заработной плате выполняется не во всех субъектах Российской Федерации. Также было установлено, что индекс Джини имеет значение выше 35 только в 8 регионах Российской Федерации, а выше 40 только в Москве. Для углубления анализа структурной дифференциации населения по доходам на практике используются различные варианты разделения населения на группы. В этом случае возникает проблема расчета коэффициента типа, характеризующего неравенство «среднего класса» (в данном случае средней 40-процентной группы населения, разделенной на три группы в пропорции 30-40-30).

Чтобы рассчитать показатели, связанные с функцией, нам нужно построить функцию распределения сотрудников по заработной плате. Одним из подходов к решению этой проблемы является использование методов вычислительной математики (например, метод сплайновой аппроксимации). Такой подход позволяет построить непрерывную функцию Лоренца и другие функции, в том числе функцию эластичности кривой Лоренца, на основе данных о распределении доходов по децильным или квинтильным группам, а также получить количественные оценки большинства показателей, используемых на практике для анализа дифференциации населения по доходам.

При разработке методологии оценки потенциала сглаживания дифференциации социально-экономического развития субъектов Российской Федерации необходимо решить ряд конкретных задач. Эти задачи включают разработку методологии ранжирования субъектов Российской Федерации по степени дифференциации населения по доходам. Этот прием должен быть относительно простым с технической точки зрения и в то же время адекватно отражать действительность. Для количественной оценки расслоения населения по доходам используются различные показатели. Однако все эти показатели лишь частично характеризуют степень расслоения населения по денежным доходам. В данном исследовании при расчете показателей дифференциации использовался подход, при котором все работники региона, ранжированные по заработной плате, делятся на две или три группы. В дополнение к традиционным критериям оценки дифференциации мы используем критерии, отражающие структурное неравенство, такие как соотношение долей доходов некоторых двух групп работников, разделенных на три группы в определенной пропорции. Для ранжирования субъектов Российской Федерации по степени неравенства в распределении средств, выделяемых на оплату труда, мы использовали данные Федеральной службы государственной статистики о средней заработной плате в децильных группах работников 85 субъектов Российской Федерации в апреле 2019 года (Росстат, 2020). Эта информация была использована для построения функции Лоренца и расчета показателей дифференциации сотрудников по заработной плате.