Дифференциальная модель социальной сегрегации

1. Базовые положения модели

Рассматривается следующий механизм социальной сегрегации основана на следующем. Процесс начинается с того, что в результате миграции возникает ситуация совместного проживания двух общин в пределах одного квартала. Если в отношениях между общинами присутствуют конфликты, то некоторые представители одной из них выезжают из квартала. На освободившиеся места въезжают новые представители другой общины. Тем самым, пропорция изменяется в пользу второй общины, в результате чего еще некоторые представители первой общины покидают квартал, освобождая места для второй общины. Таким образом, с течением времени доля второй общины в населении постоянно возрастает.

В соответствии с подходом Шеллинга [1, 2], этот процесс формализуется следующим образом. Население состоит из двух общин, которые будем обозначать Х и Y. Численность членов общин, проживающих в данном квартале в момент вре- _{л +}                                     X ( t )

мени t, обозначим, соответственно,      и y (t)

.

Модель Шеллинга базируется на следующей поведенческой гипотезе. Предполагается, что индивид удовлетворен сосед- ством в данном квартале, лишь если отношение численности «чужой» общины к численности его собственной общины не превышает некоторой величины, называемой порогом толерантности этого индивида. Значение порога толерантности не меняется с течением времени, и варьируется между индивидами: например, для кого-либо может быть достаточно не находиться в меньшинстве (т.е. порог равен единице), другой индивид может быть удовлетворен, если его община составляет не менее 30% населения квартала (в этом случае порог равен 7/3). Если текущее соотношение численностей ниже порога толерантности, то индивид удовлетворен соседством в квартале, и он остается в нем (или въезжает в квартал, если не жил в нем ранее), если же порог превышен, то индивид покидает квартал (или, не въезжает в него, если не живет в нем). При этом, для индивида, покинувшего квартал, сохраняется возможность с течением времени вернуться в него (и наоборот, новоприбывший житель может его впоследствии покинуть. Индивиды обладают полной информацией о количестве жителей квартала, принадлежащих к каждой из общин, но они не согласовывают свои действия, и не строят предположений о поведении других индивидов.

В соответствии со сформулированной выше поведенческой гипотезой, каждая община может быть охарактеризована распределением порогов толерантности среди ее членов. Для того, чтобы формализовать данную характеристику общины Х, пронумеруем ее членов в порядке невозрастания порога толерантности, и каждому из этих членов (вернее, соответствующему номеру) поставим в соответствие его значение порога толерантности. При достаточно большой численности N проведем предельный переход, получив непрерыв-f (n) ную, невозрастающую функцию      , которую назовем распределением толерантности в данной общине.

Тогда функция y x ^{f (} x ) имеет смысл максимальной численности общины Y, при которой х наиболее толерантных членов общины Х удовлетворены соседст-

вом в квартале. Таким образом, если

y <  ^xf ( x )

,

возрастает, а Аналогично, рантности в

то численность общины Х

_ y > xf (x)       _ если            , то убывает.

если распределение толе-общине Y дается функцией

g ( y ) x = yg ( y )

, то            - это максимальная численность общины Х, при которой у наиболее толерантных членов общины Y удовлетворены соседством в квартале. Ес- x < yg (y )

ли          , то численность общины Y

_x > yg (y) _    _ возрастает, а если            , то убывает.

Изобразим x = yg (y)

возможных

функции

на одном вариантов

y = ^{xf ( x} ) и

графике. Один из получаемой при

этом конфигурации представлен на рисунке 1.

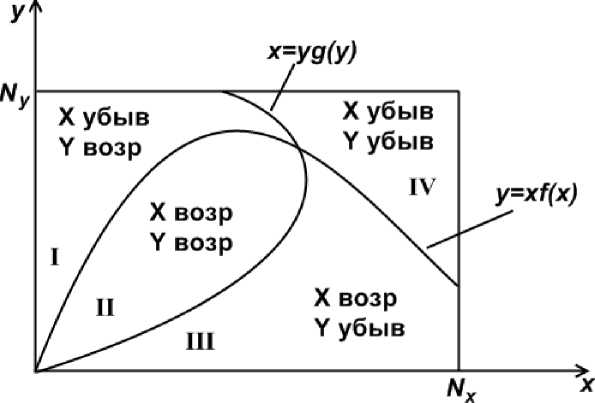
Рис. 1. Области значений переменных, в которых динамика численности членов общин X,Y, проживающих в квартале, имеет постоянное направление

Состоянию системы, при котором в квартале проживают х представителей первой общины и у – второй, соответству-

( x, y )

ет точка             прямоугольника

0 < x < Nx ,0 < y < Nv      Nx, Nv xy, где xy – максимально возможные численности об- y = xf ( x ) x = yg ( y )

щин. Кривые            и разбивают данный прямоугольник на четыре области, каждая из которых характе- ризуется определенным направлением динамики (возрастанием или убыванием) численности членов общин.

Так, если точка (x0, y0 ), изображающая начальное количество живущих в квартале членов общин Х,Y, находится в области III, то с течением времени количество представителей общины Х будет возрастать, а Y – убывать. Аналогично, если точка (x0, y0 ) расположена в области IV, то будет убывать численность жителей обеих общин.

В работах [1, 2] эти положения реализованы в качественной форме; фактически мы повторили ее выше. Основная часть данной работы посвящена дифференциальной модели, в которой эта логика принимает более конкретную форму.

Заметим также, что в указанных работах [1, 2] представлен и другой вариант модели, в котором индивиды расположены на плоскости, образуя прямоугольную решетку, и решение о выезде из квартала принимается на основании соотношения численностей членов общин в ближайшей окрестности данного индивида (а не квартала в целом). Этот вариант модели близок клеточно-автоматному подходу, который в последние годы находит все больше приложений к моделированию социальных процессов [3]. Современные варианты модели рассматривают, например, теоретикоигровую постановку [4] и сегрегацию в сетевой структуре [5].

2. Конкретизация поведенческой гипотезы и построение дифференциальной модели

Изложенный выше анализ опирался лишь на качественную зависимость между текущим соотношением численностей общин и направлением динамики, другими

словами - на зависимость между величи- x (t), y (t)

нами            с одной стороны, и зна- dx I dt, dy I dt ками величин                - с другой.

Для того, чтобы получить дифференциальные уравнения, определяющие значе-dx I dt, dy I dt z ния самих производных               (а не только их знаков), необходимо конкретизировать сформулированную выше поведенческую гипотезу.

Как указано выше, в соответствии с

x < yg ( У )  „ этой гипотезой, если            , то ленность общины Y возрастает, а x > yg ( y ), то убывает. Изобразим

чис- если

гра-

фик функции x yg ⁽ y ) , обозначим че-

xy рез 1 ее максимальное значение, у 1 - значение аргумента, при котором достига-

ется максимум, а также укажем стрелками

направление изменения численности членов общины Y - рисунок 2а (данный рису-

нок соответствует случаю, когда функция

x = yg ( У )

максимум

имеет ровно один локальный

x < Nx.

;

все рассуждения лег-

ко обобщаются на более сложные случаи).

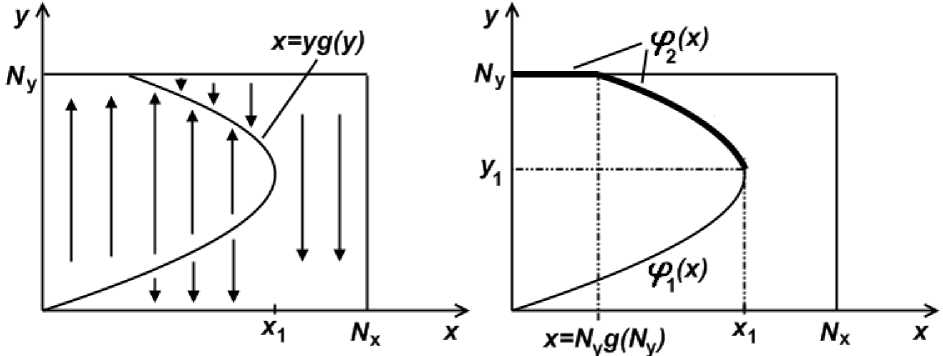
а                                  б

Рис. 2. Направление изменения численности членов общины Y и определение функций У = Ф 1 ( ^x ) У = Ф 2 ( ^x )

Обозначим через ^У ^ 1 ⁽ x ) функцию, обратную по отношению к x yg ^{( У} ) на

отрезке

У = ф₂( x )

, а через         ²       -

функцию, обратную по отношению к

^x = yg ⁽ У ) на ^у 1 ^{- y} - N y

N y при 0 ^- x ^- N y g ⁽ N y )

и равную см. рису-

x - x

При       ¹ :

x >  x

При       ¹ :

Простейшее

< °,if y <Ф 1 ( x ) , dt

- dy >  0, if Ф 1 ( x ) < У < Ф 2 ( x ) ,

. d <  ^My ■^{( x ) .}

dy

< 0

dt

дифференциальное урав-

нок 2б.

Для изменения численности общины Y

имеем следующее.

нение, отражающее данную закономерность, имеет вид dy dt

-a y ( y -Ф 1 ( x ))( y -ф 2 ( x

a y ,

:)) , 0 - x - x i , ^x 1 ^{- x -} N x .   (2)

Аналогично получим уравнение, описывающее динамику численности проживающих в квартале членов общины Х.

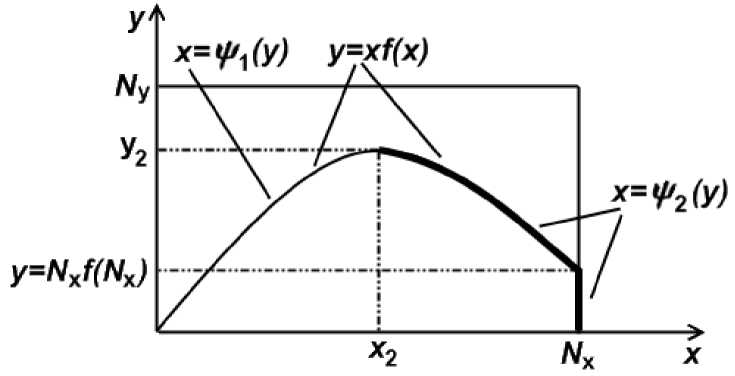
Рис. 3. Направление изменения численности членов общины Х и определение функций ^x = V 1 ( y ) ^x = V 2 ( y )

Изобразим график функции

y = ^xf ( ^x )

y = xf ( x)           x2 - x - N на отрезке 2       x

y

, обозначим через ² ее максимальное

ную

N x _np „^{0 -} y ^- N x f ( N x )

.

и рав-

x значение, 2 – значение аргумента, при

Простейшее дифференциальное урав-

котором достигается максимум – рису-

нок 3 (при этом, ограничимся случаем, ко-

„ y 2 <  N            y = xf ( x )

гда         ^y , и функция            име-

нение, качественно отражающее динамику численности проживающих в квартале членов общины Х, имеет вид

ет ровно один локальный максимум). Обо-

_x = ф, ( y )

значим через      1    функцию, обрат- y = xf ( x )

ную по отношению к            на от-

dx _ |^-P x ( x ^- V i ( y ))( x ^- Ф 2 ( у )) , ^{0 -} у ^- у 2

^dt [          ^-P x ,            У 2 ^- У ^- N y (3)

резке

0 - x - x₂

а через

x = ф 2 (y)

функцию, обратную по отношению к

Уравнения (2), (3) являются конкретизацией поведенческой гипотезы, сформулированной в п.1. Они дополняются начальными условиями

^x ( 0 ) = x 0 , y ( 0 ) = y ⁰ ,        ₍₄₎

0 < x0 < N ,0 < y < N где    xy.

dx dt

^- P ^x ( ^{x -} V 1 ( y ) )( ^{x -} V 2 ( У ) )

3. Анализ математической модели

Анализ качественной модели показал

dy dt

^-a y ( y -Ф 1 ( ^x ) )( y -Ф 2 ( ^x ) )

[1,  2], что  стационарные  решения x = 0, y = N x = N , y = 0

^y ,         ^x         являются

Уравнения для рассматриваемых стационарных решений имеют вид

асимптотически устойчивыми, в то время,

как стационарные состояния, при которых общины сосуществуют в квартале, могут быть как устойчивыми, так и неустойчи-

выми.

Изучим теперь вопрос об устойчивости стационарных решений модели (2)-(4).

Рассмотрим сначала решение

( ^{x -}Ф 1 ( y ) )( ^{x -}V 2 ( y ) ) = ⁰

( У -Ф 1 ( ^x ) )( У ^-Ф 2 ( ^x ) ) = ⁰

Количество стационарных решений за-

висит от вида функций распределения то-

x = 0, y = N y

В его окрестности уравнения (3), принимают вид

лерантности

У = f ( ^x )

,

x = g ^{( У} ) . Каж-

дое из них может быть исследовано на ус-

dx = -P x dt dy   ay(y-Ф(x))(y - Ny)

тойчивость – например, с помощью метода исследования устойчивости по первому приближению.

Продемонстрируем это для случая линейных функций распределения толерант-

ности:

Очевидно, при достаточно малых ^ , в

-              Nv -8<У

dx / dt< 0 dy / dt > 0 имеем ^ux ' ^ut< ^v, ^z

. Отсюда

f (^x) = a^-b^x, g (y ) = c^-ky (13)

Тогда максимальная численность общины Y, при которой х наиболее толерантных членов общины Х удовлетворены соседством в квартале, дается функцией

следует, что если начальные

лежат в этой области, то

N (t) ^ N      „

^{X 7}     y при t ^^, что

условия (4)

x (t) ^ 0

,

согласуется

с результатом анализа качественной модели [1, 2].

Аналогично доказывается асимптотическая устойчивость решения

^x = Nx, y = 0

Перейдем к исследованию стационарных решений, описывающих состояния, при которых общины сосуществуют в квартале. В окрестности каждого из них уравнения (3), (2) принимают вид

y = xf ( x ) = ax - bx²

Максимальное значение функции (14)

x_?= a / (2 b)

достигается при 2          , оно равно y2 = a2/(4b)  „

2           . Чтобы найти обратные функции x = V1(y ), x = v 2 ( y ) , выразим х через у из равенства (14), получим

( _A a -aa ■ V1^(y )=      2b

_z x a+aa ■ ^v2^(y )=-----2b

,

Аналогично, максимальная численность общины Х, при которой у наиболее толерантных членов общины Y удовлетворены соседством в квартале, дается функцией

x = yg ( y ) = cy - ky2

(21),(22), и учитывая (23), получаем, что x,y ss удовлетворяют системе

Максимальное значение функции (16)

достигается при

y = c / ( 2 d )

¹           , оно равно

x1 = c²/ (4 d )

a ) a - 4 bys ----z---— 0

2 b 7      4 b²

c У c2 - 4 kx ----s-—- — 0

2 k 7      4 k г

имеем

Ф1 ( x ) =

Ф2 (x)

Для обратных функций

c - 4 c²- 4 kx

2k

c + 42'²- 4 kx

2k

Система (9), (10) принимает в данном

случае вид

dx R

— = ^-P x x dt

a — 0^ — 4 by

2b

Y

x

7V

a + 7a² — 4 by

2b

dy dt

^—ay I y

c — 4 c²- 4 kx || c + 4 c²- 4 kx

--------------------II y--

2 k       II           2 k

Уравнение (18) можно записать в виде

(

dx r

— = ^-Px x dt

V

откуда

dx

—I

—

a

--+

2b

7 a²-⁴by

2b

(

x

—

V

a

2b

—

7 a²— 4 by

²b   ⁷,(20)

dt

в x  x

-

a

-

a²

—

4by

2 b 7

4b²

⁷,(21)

Аналогично, из (19) имеем

dy

— — -a y dt

y

^

Рассмотрим

стационарного что

c I c - 4 kx

2k

^

⁴k^{2  7}(22)

вопрос об устойчивости

(x_s, y_s)

решения ^ss

такого,

x > 0 ys > 0

ss ,,

описывающего ситуацию, при

которой

две общины сосуществуют в квартале.

Приравнивая к нулю производные в

Матрица Якоби, взятая в стационарных состояниях, удовлетворяющих уравнениям (24), (25), имеет вид

(      b

—2pxs I xs —

J ( xs , ys ) =

a ^ 2b 7

ays

^{в x}s

b b     c

-^2ays I ys^— —

Если оба собственных значения матрицы вида (26) имеют отрицательные дейст-

вительные части, то стационарное реше-

_ (xs, ys)

ние ^ss асимптотически устойчиво, если же хотя бы одно из собственных значений имеет положительную действитель-

ную часть, то стационарное решение неустойчиво.

Заметим, что, помимо решений рассмотренных выше стационарных решений (5), (8), (23), система (18), (19) имеет также

xs — ys — 0  „ стационарное решение s s . Оно не может быть изучено методом исследования устойчивости по первому приближению, так как матрица Якоби в точке xs — ys — 0

s s    является нулевой матрицей, и ее собственные значения равны нулю, что

не позволяет сделать вывод относительно устойчивости. Однако, неустойчивость этого стационарного решения может быть

показана путем анализа знаков производ-dx / dt , dy / dt ных      , y в окрестности этой точ ки.

4. Заключение

Представленная в настоящей работе модель описывает механизм социальной сегрегации, основанный на неудовлетворенности индивидов проживанием «среди чужих», сформулированном здесь в виде

поведенческой гипотезы. Один из возможных социологических сценариев описывает полный исход одной из общин из квартала. Пусть, например, изначально община Х находилась в меньшинстве, но некоторые из ее членов были удовлетворены текущим соотношением. Однако по мере того, как другие, менее толерантные, члены общины Х покидают квартал, соотноше- ние меняется еще более в польщу общины Y. Ввиду этого, некоторые из ранее удовлетворенных членов общины Х становятся неудовлетворенными, и также покидают квартал. Этот процесс может иметь два исхода. В одном из них вся община Х покидает квартал, в другом исходе устанавливается совместное проживание общин в некоторой пропорции.