Дифференциальная регистрация поляризационно-модулированных оптических сигналов

Поляризационно-оптические измерения остаются на протяжении многих лет одним из самых эффективных способов исследования широкого круга явлений в атомной и молекулярной физике, физике твердого тела, физической оптике [1–8]. Эти измерения находят также широкое применение в повседневной инженерной практике. В последнее время заметно усилился интерес к одному из видов поляризационно-оптических измерений — к измерениям малого двулучепреломления прозрачных сред. В значительной мере это обусловлено применением поляризационных методов для контроля процессов изготовления оптических и оптоэлектронных материалов, широко используемых в квантовой электронике, и значительным повышением требований к качеству этих материалов. В связи с этим возрастает необходимость все более прецизионных измерений, все большее значение приобретает проблема совершенствования методик, повышения их чувствительности и точности [9–13].

Одним из наиболее перспективных способов решения указанной проблемы в настоящее время представляется использование оптических схем, в которых традиционная процедура измерений с модуляцией поляризации пробного излучения сочетается с дифференциальной регистрацией полезных сигналов. Этот способ находит все большее применение как высокочувствительный инструмент для широкого круга исследований [5, 6, 12–15]. Рассматриваемое сочетание, с одной стороны, позволяет проводить измерения переменных сигналов, методы обработки которых хорошо развиты, а с другой — дифференциальные схемы приводят в ряде случаев к подавлению шумов и повышению точности и чувствительности измере- ний. Подробные экспериментальные исследования и предварительный качественный анализ возможностей подавления шумов в таких схемах при измерении постоянного двулучепреломления прозрачных объектов были ранее выполнены в работе [16]. Эти исследования показали, что применение дифференциальных схем может существенно повысить чувствительность измерений, однако такое повышение происходит не для всех традиционно применяемых измерительных конфигураций. Более того, степень подавления шумов существенно зависит как от свойств исследуемых объектов, так и от параметров экспериментальной установки. По этим причинам важным является изучение различных условий измерения и поиск оптимальных.

Проблема оптимизации содержит много параметров, и ее подробный экспериментальный анализ является достаточно сложным. Теоретическое исследование чувствительности и точности модуляционных измерений с использованием дифференциальных схем регистрации требует решения двух взаимосвязанных задач: адекватного описания наблюдаемой в эксперименте величины и вычисления погрешностей ее измерения. Главной целью данной работы является решение первой из этих задач — теоретическое описание сигналов, детектируемых в модуляционных схемах поляризационных измерений с дифференциальной регистрацией. Рассмотрены основные используемые в настоящее время типы построения поляризационных анализаторов и проведено их сравнение между собой.

МОДИФИЦИРОВАННЫЕ ИЗМЕРИТЕЛЬНЫЕ КОНФИГУРАЦИИ

На рис. 1 показана схема измерений оптической

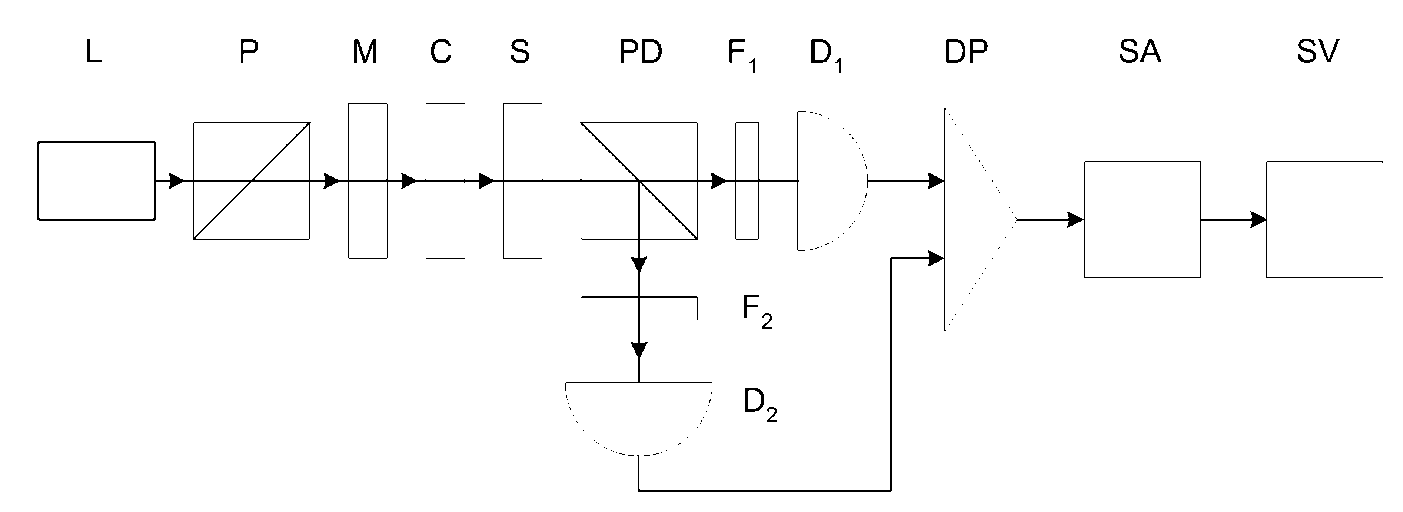
Рис. 1. Блок-схема экспериментальной установки.

L — лазер; P — поляризатор; M — модулятор; C — компенсатор; S — исследуемый образец; PD — поляризационный делитель; F 1 , F 2 — аттенюаторы; D 1 , D 2 — фотодиоды; DP — дифференциальный преобразователь; SA — анализатор спектра; SV — селективный вольтметр

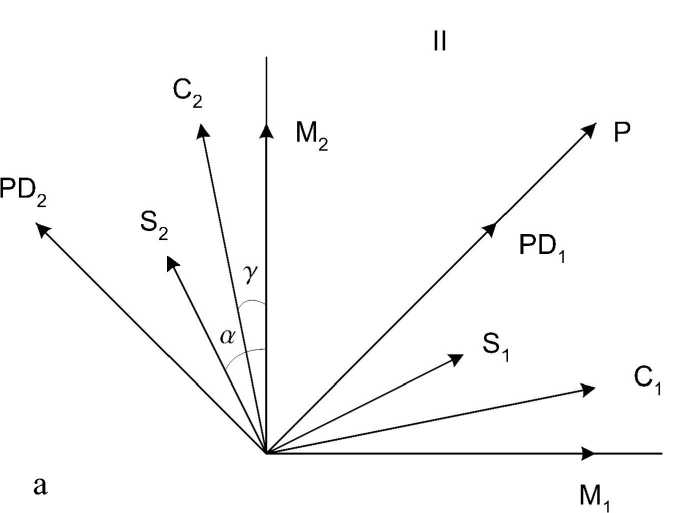
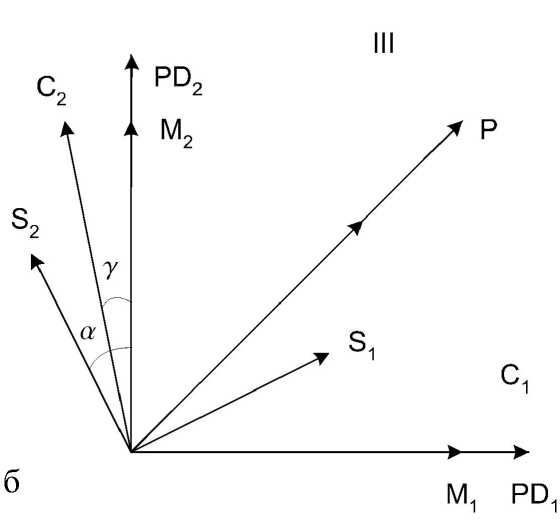
Рис. 2. Ориентации главных оптических осей элементов установки: модулятора ( M 1 и M 2 ), поляризатора ( P ), поляризационного делителя ( PD 1 и PD 2 ), компенсатора ( C 1 и C 2 ), образца ( S 1 и S 2 ). Угол ориентации осей компенсатора γ выбирается из условия равенства нулю выходного сигнала в отсутствие образца. а — соотв етствует конфигурации II, б — конфигурации III [7]

анизотропии с модуляцией поляризации зондирующего излучения и дифференциальной схемой подавления шумов [14, 16]. Свет от лазера L проходит через поляризатор P, который улучшает стабильность положения плоскости поляризации, затем через ф отоупругий модулятор М, создающий периодически меняющуюся во времени разность фаз между ортогональными линейно поляризованными компонентами поля, что приводит к периодическому изменению состояния поляризации. Модулированное по поляризации пробное излучение проходит далее через компенсатор С, исследуемый образец S и попадает на поляризационный делитель PD. Компенсатор — плоскопараллельная пластинка с известным двулучепреломлением ϕc . Сигнал с выхода дифференциального преобразователя DP, пропорциональный раз- ности фототоков фотодиодов D1 и D2 , подается на анализатор спектра SA (в ряде случаев вместо спектроанализатора удобнее применять синхронный детектор). Селективный вольтметр SV предназначен для анализа шумов выходного сигнала спектроанализатора.

Схема на рис. 1 дополнена двумя аттенюаторами F 1 и F 2 . Они использовались в нашем эксперименте [16] и предназначались для внесения регулируемой асимметрии в каналы регистрации, что давало возможность исследовать характер работы схемы, в частности проанализировать степень подавления избыточных шумов при различных условиях балансировки. Заметим, что в традиционных схемах измерений с модуляци ей поляризации, применяемых, например, в эллипсометрии [7], в отличие от схемы, изображенной на рис. 1, вместо поляризационного делителя используют анализатор, излучение после которого регистрируется одним фотодетектором.

На рис. 2 показаны два практически применяемых варианта взаимных ориентаций оптических осей элементов, которые при использовании обычного анализатора и одного фотодетектора обозначаются часто как конфигурации II и III [7]. В дальнейшем мы сохраним эти обозначения и для рассматриваемых нами схем. В конфигурации II поляризатор развернут под углом 45° к главным осям модулятора M1 и M2 , главные оси поляризационного делителя ориентированы — одна вдоль оси поляризатора, другая перпендикулярно ей. Вектора PD1 и PD2 на рис. 2 указывают направления поляризаций двух пучков света, выходящих из поляризационного делителя. В конфигурации III взаимные ориентации поляризатора и модулятора совпадают с конфигурацией II, а оси поляризационного делителя развернуты на 45°. Ориентация оптических осей исследуемого образца может повлиять на характер работы всей измерительной схемы, поэтому в тех случаях, когда эта ориентация известна и необходимо измерить только абсолютную величину двулучепреломления, образец устанавливают так, чтобы в конфигурации II его главные оси S1 и S2 совпадали с главными осями модулятора, а в конфигурации III — были повернуты на 45° по отношению к осям модулятора. В данной работе мы считаем ориентацию осей образца известной, однако с целью более полного анализа при теоретическом рассмотрении мы исследуем, в частности, и случай, когда оси индикатрисы образца составляют угол α с осями модулятора (см. рис. 2). Заметим также, что если материал образцов по каким-либо причинам не является однородным, а такие образцы встречаются часто, то главные оси индикатрисы могут иметь различную ориентацию в разных частях образца [11, 12]. На рис. 2 изображена также ориентация главной оптической оси комп енсатора, угол ориентации которой γ выбирается таким образом, чтобы обеспечить нулев ой сигнал при отсутствии образца. Это позволяет скомпенсировать постоянное двулучепреломление оптических элементов установки.

СИГНАЛ ОПТИЧЕСКОГО ДВУЛУЧЕПРЕЛОМЛЕНИЯ

Анализ чувствительности и точности измерений требует решения двух задач — адекватного теоретического описания наблюдаемой в эксперименте величины и вычисления погрешностей ее измерения. В описываемых нами экспериментах измеряемой величиной является двулучепреломление исследуемых образцов, которое определяется по величине выходного сигнала анализатора спектра, т. е. по величине напряжения или тока на выходе

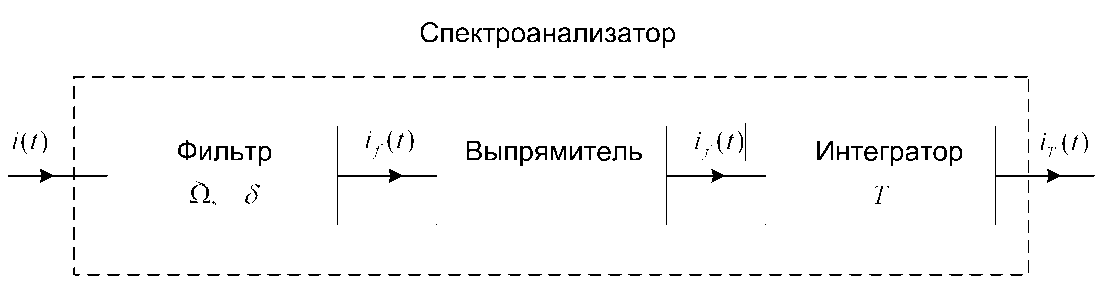
Рис. 3. Упрощенная блок-схема спектроанализатора

видеодетектора. Для теоретического описания выходного сигнала анализатора и спектра его флуктуаций рассмотрим более подробно структурную схему анализатора, которая изображена на рис. 3.

Сигнал с выхода дифференциального преобразователя i ( t ), пропорциональный разности токов фотодетекторов двух каналов регистрации i ( t ) = i 1 ( t ) - i ₂( t ), проходит через фильтр с полосой пропускания 5 вблизи частоты Q*. После фильтра сигнал поступает на выпрямитель. Выходной сигнал выпрямителя i_f ( t ) интегрируется (усредняется) по времени T с помощью интегратора. Рассматриваемые выпрямитель и интегратор моделируют линейный видеодетектор анализатора спектра C4-55, использованного в работах [11, 16]. В нашем анализе, таким образом, напряжению на выходе видеодетектора спектроанализатора будет соответствовать выходной сигнал интегратора, который описывает наблюдаемую в экспериментах по измерению малого двулучепреломления величину. Вычисление среднего значения этой величины и составляет основную задачу данной работы.

Сигнал на выходе фильтра можно определить либо с помощью временнóй характеристики фильтра h(t), либо с помощью его спектральной to характеристики Y(ш) = jh(t)exp(iшt)dt:

t if (t) = J h (t — t') i (t ')d t' =

-to to

= j Y ( ш ) i ( ш )exp( - i ш t )d ш /2 n ,          (1)

-to

1 t + t

S ( $ ) = i i_T ( t )} = - j i \i( ( t *)|)d t '.         (3)

Tt

Получаемое среднее, зависящее от частоты фильтра $%^ как от параметра, будем сопоставлять сигналу, соответствующему экспериментальному измерению двулучепреломления исследуемого образца. Для произвольного случайного процесса i(t)

это среднее зависит как от времени "включения"

интегратора t , так и от интервала усреднения T .

В анализируемых здесь экспериментах [16], как и в большинстве подобных опытов, сигнал определяется не путем усреднения по ансамблю опытов, а путем усреднения по времени. Это достигается увеличением времени накопления T . Мы предполагаем, что рассматриваемые нами случайные процессы обладают свойством эргодичности и, таким образом, оба способа усреднения дают совпадающие результаты [18].

S (i%^)

Вычислим величину

для двух рассматри-

ваемых здесь поляризационных схем II и III. Для этого необходимо вначале выполнить расчет фототоков, который при известных параметрах оптического тракта полностью аналогичен приведенному в работе [11]. В случае произвольной величины двулучепреломления образца и компенсатора получающиеся формулы чрезвычайно громоздки. Приведем здесь результаты для некоторых важных частных случаев.

Для малого двулучепреломления образца ϕ (при этом, должно быть мало и остаточное двулу- чепреломление оптических элементов и компенсатора) выходной разностный ток для конфигурации II равен to где i(ш) =j i(t)exp(iшt)dt спектр фототока.

i ( t ) = i ₀ k ( k 1 - k ₂ + ( k 1 + k ₂ ) cos( A sin Q t ) ) -

- i 0 k ( ф cos2 a sin( A sin Q t ) ) ,            (4)

Время "включения" фильтра в расчетах полагаем равным to, что в дальнейшем позволит исключить рассмотрение переходных процессов и пользоваться не динамической, а статической разрешающей способностью [17]. При этом выходной сигнал спектроанализатора iT (t) равен

1 t+T iT(t) = - j if (t)|dt' = t+T

to

О t + T        to                                       1

= — j Re J y ( ш ) i ( ш )exp( - i ш t ')— d t '.

T                        2 π

t

Определяемая соотношением (2) величина i_T ( t ) является случайной и должна быть усреднена по ансамблю:

где i ₀ — постоянная величина, определяемая интенсивностью лазера на входе в оптический тракт; ф _т = A sin Q t — разность фаз ортогонально поляризованных компонент, создаваемая модулятором; A и Q — амплитуда и частота модуляции; а — угол между оптической осью образца и осями модулятора; k — коэффициент, учитывающий полное пропускание оптического и электронного трактов и, в частности, преобразование ток— напряжение, осуществляемое дифференциальным преобразователем DP (см. рис. 1); k ₁ и k ₂ — коэффициенты пропускания фильтров F₁ и F₂ . При написании соотношения (4) мы учли, что остаточное двулучепреломление остальных элементов скомпенсировано.

В общем случае выходной разностный сигнал является случайной функцией времени, поскольку все входящие в формулу (4) параметры схемы — i0, k, k1, k2, A, Q — могут флуктуировать. Случайной является и спектральная компонента фототока i(ω), которую мы представим в виде суммы среднего по ансамблю наблюдений значения i(ω) и флуктуирующей добавки 5 i (to): i (to) = = i(to) + 5i(to). Флуктуирующая добавка предполагается малой со средним значением, равным нулю.

Спектр δ i ( ω ) — плавная функция, слабо меняющаяс я в пределах полосы пропускания фильтра δ , а i ( ω ), как следует из (4), содержит набор дискретных линий на частотах l Q , где l = 0,1,....

i ( to ) = 2 п i₀ k ( k₁ - k 2 + ( k₁ + k 2 ) J₀( A ) ) 8 ( to ) +

+2п i0 k (k + k2 )x x| JJ2,(A)(8(to + 2lQ) + 8(to-2lQ)) +

V

+£J2 l+1( A )i (8( to + (2l + 1)Q) + 8( to -(2l + 1)Q))x l=0

xф cos2 a ^ ,                                       (5)

где 8 ( to ) — дельта функция, J l ( A ) — функции Бесселя, а буквой i без индексов и аргументов обозначена мнимая единица.

Предполагая, что функция передачи фильтра имеет прямоугольную форму с полной шириной 5 и центральной частотой Q*, равной частоте модуляции поляризации пробного излучения Q, получим i (t) = — J D cos (Qt'- a )| dt',          (6)

Tt где

D = ( Im C ) + ( Re C ) ²;    tg a = Im C / Re C ;

C = ii ₀ k ( k ₁ + k ₂)J ( A ) Y ( Q ^ cos 2 a +             (7)

Q+ 5 /2

+ Y ( Q ) J 5 i ( to )exp( - i ( to -Q ) t 'd to /2 п .

Q- 5 /2

Учитывая, что Q T >>  1, а флуктуации фототока малы i ( to ) >>  5 i ( to ), окончательно получаем

S ( Q ) = —i₀k ( k ₁ + k ₂) J ₁( A ) Y ( Q ) Ф cos2 a .    (8)

π

Среднее значение наблюдаемой не зависит ни от времени, ни от интервала усреднения.

Чтобы оценить характер работы балансной схемы с модуляцией при больших величинах двулучепреломления образца, приведем еще результат для частного случая, когда остаточной анизотропией установки можно пренебречь, а ориентация осей образца совпадает с ориентацией осей модулятора. В этом случае

S ( Q ) = —i ₀ k ( k ₁ + k ₂)J₁( A ) Y ( Q ) sin ф .     (9)

π

Расчет величины S ( Q ) для конфигурации III может быть выполнен аналогично. В случае малой анизотропии образца для конфигурации III выходной разностный ток равен

i ⁽ t ) =

= i ^{0 k} ( ^k 1 ^{- k} 2 ⁺( ^k 1

+ k ₂ ) ( ф sin 2 a )sin( A sin Q t ) ) .

Это выражение в отличие от формулы (4), соответствующей схеме II, приводит к спектру, не содержащему линий на четных гармониках частоты Q :

i( to ) = 2 п i ₀ k ( k ! - k 2 ) 8 ( to ) -

-2n i0 k (k! + k2 )x xj^ J2 l+1 (A )i (8(to + (2l + 1)Q) + 8(to -(2l + 1)Q))x l=0

x ф sin2 a ,                                           (11)

Наличие или отсутствие в спектре фототоков сильных компонент на четных гармониках частоты модуляции не является существенным при вычислении сигнала спектроанализатора, поскольку мы предполагаем, что анализатор настраивается на частоту Q , равную частоте модуляции Q и в полосу пропускания δ не попадает никакая другая гармоника. При этом выходной сигнал с учетом условия компенсации:

S ( Q ) = —i₀k ( k ₁ + k ₂)J₁( A ) Y ( Q ) ф sin2 a . (12) π

В случае сильного двулучепреломления образца, ориентированного под углом a = п /4 к осям модулятора, когда остаточным двулучепреломлением оптического тракта можно пренебречь, снова получаем формулу (9). Заметим, что как для схемы II (см. (8)), так и для схемы III (см. (12)) величина сигнала двулучепреломления зависит от ориентации оптических осей образца. Максимальный сигнал, наблюдаемый в схеме II при a = 0 , совпадает с максимальным сигналом, наблюдаемым в схеме III при a = п / 4 . (Совпадают и формулы, соответствующие сильной анизотропии образца). Подоб- ное совпадение означает, что с точки зрения оптимизации наблюдаемых обе схемы могут рассматриваться как равноправные. Это однако не означает, что возможности схем полностью эквивалентны. Как показал наш предварительный анализ погрешностей измерений, проведенный в работе [16], наличие или отсутствие в спектре фототоков (см. (5) и (12)) сильных компонент на четных гармониках частоты модуляции оказывает существенное влияние на флуктуации регистрируемых сигналов. Это приводит к существенному различию в уровнях шумов измерений, и схемы II и III обладают различной чувствительностью и обеспечивают разную точность измерений.

Анализ, выполненный в работе [16], носит качественный характер, учитывает наличие только одной спектральной компоненты шумов, а также флуктуации только интенсивности пробного света. В реальных условиях флуктуации распределены по спектру, поэтому более обстоятельный анализ требует учета всех тех фурье-компонент шума, которые в конечном итоге попадают в полосу пропускания системы регистрации. Помимо этого представляется целесообразным рассмотреть иные кроме пробного света источники случайных погрешностей. Подобный детальный анализ различных источников шумов выполнен в работе [19].

Эта работа частично поддержана Российским фондом фундаментальных исследований (грант № 06-02-17219-а).