Дифференциальное исчисление

Дифференциальное исчисление создано Ньютоном и Лейбницем сравнительно недавно, в конце XVII столетия. Тем более поразительно, что за долго до этого Архимед не только решил задачу на построение касательной к такой сложной кривой, как спираль, но и сумел найти максимум функции f(x) = x²(a — x). В XVII в. на основе учения Г. Галилея о движении активно развивалась кинематическая концепция производной.

Пусть мы имеем функциюу = f(x), определенную в некотором промежутке. При каждом значении аргумента xиз этого промежутка функция у = f(x) имеет определенное значение. Пусть аргумент x получил некоторое (положительное или отрицательное- безразлично) приращение △ x. Тогда функция у получит некоторое приращение △ у. Таким образом: f'(x) = lim —при значении аргумента x будем иметь у = f(x), при значении △х^0 △^ аргументаx +△ xбудем иметь у +△ у = f(x +△ x).

Найдем приращение функции △ у : △ y = /(x+^x) — /(x)

Составим отношение приращения функции к приращению аргумента:

△У /(x+Дx)—/(x)

△ x

△ x

Найдем предел этого отношения при ^{Δ → 0} . Если этот предел существует, то его называют производной данной функции /(x) и обозначают / ' (x).  Таким образом, по определению,/ ' (x) = lim — или / ' (x) =

△ x^0 △ x

,.   /(x-дx)-/(x)

lim -----------

△ x^0     △ x

Производной данной функции у = /(x)по аргументу x называется предел отношения приращения функции Δy к приращению аргумента Δx, когда последнее произвольным образом стремится к нулю.

Заметим, что в общем случае для каждого значения x производная/ ' (x) имеет определенное значение, т.е. производная является также функцией от x.

Наряду с обозначением / ' (x) для производной употребляются и другие обозначения, например у ' ,у Х , ^^ .

Конкретное значение производной при x = а обозначается/ ' (а). Операция нахождения производной от функции /(x) называется дифференцированием этой функции.

Теперь дадим не менее важное геометрическое истолкование производной. Для этого нам прежде всего потребуется определение касательной к кривой в данной точке.

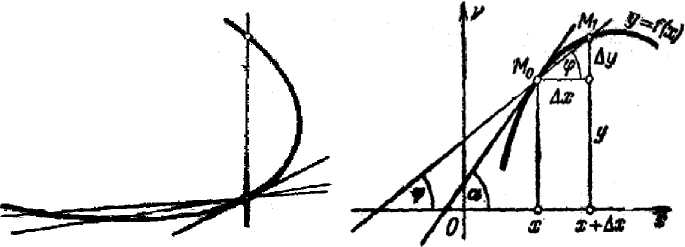
Рис. 1.                           Рис. 2.

Пусть имеем кривую и на ней фиксированную точку M 0 . Возьмем на кривой точку M 1 и проведем секущую M 0 M 1 (рис. 1). Если точка M 1 неограниченно приближается по кривой к точкеM 0 , то секущая M 0 M 1 занимает различные положения M 0 M 1 ’, M 0 M 1" и т. д.

Если при неограниченном приближении точки M 1 , по кривой к точке M₀ с любой стороны секущая стремится занять положение определенной прямой M 0 T, то эта прямая называется касательной к кривой в точке M 0 .

Прямая заданная уравнением: g(x) = /(x₀) + / ' (x₀ — x₀) называется касательной к графику функции / в точке х₀.

Рассмотрим функцию /(x) и соответствующую этой функции кривуюу = /(x).

В прямоугольной системе координат (рис. 2). При некотором значении х функция имеет значениеу = /(х). Этим значениям х и у на кривой соответствует точка М0(х,у). Дадим аргументу х приращение Дх. Новому значению аргумента х + Дх соответствует «наращенное» значение функции у + Ду = /(х + Дх).

Соответствующей ему точкой кривой будет точкаМ 1 (х + Дх, у + Ду). Проведем секущую M 0 M 1 и обозначим через фугол, образованный секущей с положительным направлением оси Ox . Составим отношение — Из рисунка 1 Ду непосредственно усматриваем, что — = tg^.

Если теперь Дх будет стремиться к нулю, то точкаM 1 перемещаться вдоль кривой, приближаясь к M₀. Секущая M₀M 1 будет поворачиваться вокруг точки М₀и угол ф будет меняться с изменениемДх. Если при Дх ^ 0 угол р стремиться к некоторому пределуа, то прямая, проходящая через М₀ и составляющая с положительным направлением оси абсцисс угол α, будет искомой касательной. Нетрудно найти ее угловой коэффициент: tga = lim tap = lim 7^ = / ' (х).

Дх^0       Дх^0 Дх

Следовательно, / ' (х) = tga, т.е. значение производной / ' (х) при данном значении аргумента х равняется тангенсу угла, образованного с положительным направлением оси Ох касательной к графику функции / ' (х) в соответствующей точке M₀(x,y).

Дифференциальное исчисление широко используется при исследовании функций. С помощью производной можно найти промежутки монотонности функции, ее экстремальные точки, наибольшие и наименьшие значения.