Дифференциальные модели в физике

5 course of physics and mathematics faculty,

VGPU

Russia, Voronezh

Supervisor: Obukhovsky VV Professor of the Department of Higher Mathematics DIFFERENTIAL MODELS IN PHYSICS.

The article is devoted to differential models in physics and consideration on a practical example.

Дифференциальные    модели,    экономика,    математическое моделирование.Обычно, когда физическую задачу, связанную с изменяющейся ситуацией, хотят свести к математической, то рассматривают два близких момента: «было» и «стало» и затем используют различные законы сохранения (массы, энергии, преломления и т.д.), чтобы связать их воедино. Многие задачи при таком подходе сводятся к дифференциальным уравнениям.

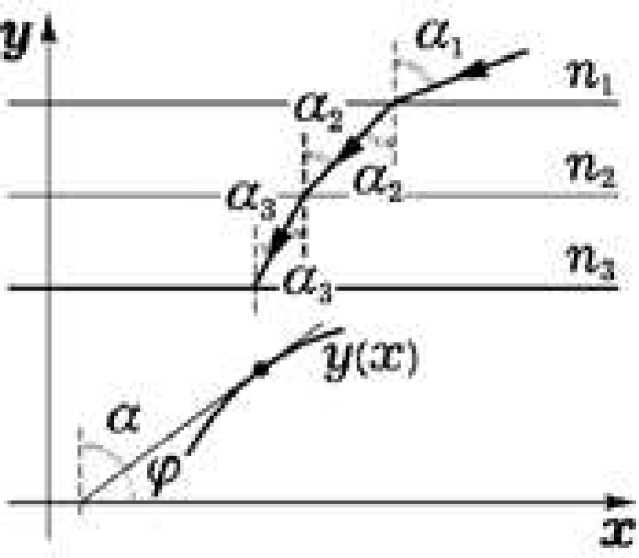
Такую связь можно рассмотреть на примере нахождения траектории световых лучей в верхней полуплоскости, при условии, что коэффициент преломления меняется по закону n(y)=n 0 /y.

При прохождении света через границу раздела двух сред выполняется sin «1    П2         _                       _ закон преломления:----= — или n1sina1 = n2sina2, где ^i - угол падения,

Sin « 2     П 1

( 2 - угол преломления, n 1 , n₂ показатели преломления сред относительно вакуума. Если представить теперь неоднородную среду, то закон преломления записывается:

n1slna1 = n2slna2 = n3slna3 = ••• = const, nsln a = const

Переходим от угла падения а к углу наклона ф = f — a, используем геометрический смысл производной, tg ф = у,   , и получаем дифференциальное уравнение для траекторий, по которым движется свет в нелинейной среде:

n sin a = n sin ( f - ф) z

n = n cosф = , ^1+1д2ф (у , )2 = C2n2.

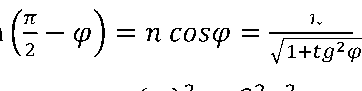
По условиям задачи n(y)=n0/y, поэтому переобозначением константы

Сн0 ^ С,

. С2          „ С2

1 + (У')2=У2■   (у)2^—1

dу _ Ус2 — у2

dx

У

[^=

УС2

У

—

= = ± [ dx, — ^ у2

—

у2 = ±(x + Ci),

(x + С1)2 + у2 = С2

Это множество полуокружностей, поскольку верхней полуплоскости.

все дело происходит в

¹ + (У , )² = С²у² . У =

Рассмотрим случай, если п(у) = п0у , то

±VCV’—1,;/== = ±dx, J ^£= = ±С f dx, !»1Су + 7(Су)2 —1| = ±(Сх + С1).

Преобразовав, получится у(x) =-ch(Cx + С1) , что С>0, т.е. свет распространяется по цепным линиям.

Тот же ответ можно получить быстрее, если искать решение в параметрическом виде х=х(р), у=у(р). Пусть у,=р, тогда у = ^^Р- • Итак, p = shq, dx = -^- = -1-d (^) =    x(q) =р—С1    и,    объединяя

OIL (V      о/L (V     \ V /       V                    V зависимости x(q), y(q), получаем у(x) = |ch(Cx + С1).

Из-за нелинейного вхождения производной в исходное уравнение, его надо проверить на особые решения. В случае общего уравнения F(x,y,y,)=0, это означает, что с системе F(x,у,у’) = 0, ^^у^-) = о надо избавиться от у и получившуюся дискриминантную кривую уs(x) проверить, что, во-первых, она является решением; а, во-вторых, в каждой точке х0 она касается какого-то другого решения уравнения F(x,у,у,') = 0. В данном конкретном случае = 0 ^ у, = 0 получаем два решения у5 (x) = ±1 , из которых надо оу                                                      С выбрать только плюсовое, так как функция у должна быть положительной.