Дифференциальные уравнения первого порядка
Автор: Носирова Д.А.
Журнал: Экономика и социум @ekonomika-socium
Рубрика: Основной раздел
Статья в выпуске: 11 (66), 2019 года.
Бесплатный доступ
Данной статье рассматривается дифференциальные уравнения и пример с задачей
Ду, переменная, функция, пример, задача, решения
Короткий адрес: https://sciup.org/140246113
IDR: 140246113 | УДК: 01.01.02
Текст научной статьи Дифференциальные уравнения первого порядка
Что нужно знать и уметь, для того чтобы научиться решать дифференциальные уравнения? Для успешного изучения диффуров надо хорошо уметь интегрировать и дифференцировать.
В 95% случаев в контрольных работах встречаются 3 типа дифференциальных уравнений первого порядка: уравнения с разделяющимися переменными, которые мы рассмотрим на этом уроке; однородные уравнения и линейные неоднородные уравнения. Начинающим изучать диффуры советую ознакомиться с уроками именно в такой последовательности, причём после изучения первых двух статей не помешает закрепить свои навыки на дополнительном практикуме – уравнения, сводящихся к однородным.
Есть еще более редкие типы дифференциальных уравнений: уравнения в полных дифференциалах, уравнения Бернулли и некоторые другие. Наиболее важными из двух последних видов являются уравнения в полных дифференциалах, поскольку помимо данного ДУ я рассматриваю новый материал - частное интегрирование.
Сначала надо вспомнить обычные алгебраические уравнения. Они содержат переменные и числа. Простейший пример: Зх = 12# Что значит решить обычное уравнение? Это значит, найти множество чисел, которые удовлетворяют данному уравнению. Легко заметить, что детское уравнение 3* = 12 имеет единственный корень: 1 = ^. Для прикола сделаем проверку, подставим найденный корень в наше уравнение: 34 = 12
12 = 12 — получено верное равенство, значит, решение найдено правильно. Диффуры устроены примерно так же!
Дифференциальное уравнение первого порядка в общем случае содержит:
-
1) независимую переменную *;
-
2) зависимую переменную (функцию);
-
3) первую производную функции: У .
В некоторых уравнениях 1-го порядка может отсутствовать «икс» или (и) «игрек», но это не существенно - важно чтобы в ДУ была первая производная -^ , и не было производных высших порядков - -^ , -^ и т.д.
Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение - это значит, найти множество всех функций, которые удовлетворяют данному уравнению. Такое множество функций часто имеет вид ■^=^;с’^ ( С— произвольная постоянная), который называется общим решением дифференциального уравнения .
Найти частное решение дифференциального уравнения е Решение: сначала найдем общее решение. Данное уравнение уже содержит готовые дифференциалы ^и dx , а значит, решение упрощается. Разделяем переменные: ey e x dy- 2xdx = 0 §y ■ e~x dy = 2xdx v , 2xdx eydy = 2^ dx Интегрируем уравнение: Интеграл слева – табличный, интеграл справа – берем методом подведения функции под знак дифференциала: ^ = Z+c Общий интеграл получен, нельзя ли удачно выразить общее решение? Можно. Навешиваем логарифмы на обе части. Поскольку они положительны, то знаки модуля излишни: Tt r 7 = ^(0' +0, где C =co?2si Итак, общее решение: Найдем частное решение, соответствующее заданному начальному условию X0) . В общее решение вместо «икса» подставляем ноль, а вместо «игрека» логарифм двух: In 2 = ln(s° + Q Более привычное оформление: jv(0) = h(s° +Q = ln(l + Q = In 2 =>C = 1 Подставляем найденное значение константы C=1 в общее решение. Ответ: частное решение: V = W Проверка: сначала проверим, выполнено ли начальное условие у(0) = 1п2 Я0) = Це° + 5 = 1п(1 + 1) = 1п2 Теперь проверим, а удовлетворяет ли вообще найденное частное решение у ^ +^ дифференциальному уравнению. Находим производную: Смотрим на исходное уравнение: ®^ ^ ^^ ° - оно представлено в дифференциалах. Есть два способа проверки. Можно из найденной производной выразить дифференциал ^у : Подставим найденное частное решение -^ ^е +^ и полученный , 2хе* dx яу — № дифференциал ^ + ^ в исходное уравнение е?^У ^^ °: e^+i)-<^f^_ 2^х=0 (Z +D gh^+i) ^ 2хе^х _ 2^ = 0 (^ +1) Используем основное логарифмическое тождество s /+1).,-1 ^^-г^д О' +D 2хе* ”* dx - 2xdx= 0 2xdx- 2xdx= 0 0 = 0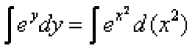
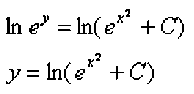
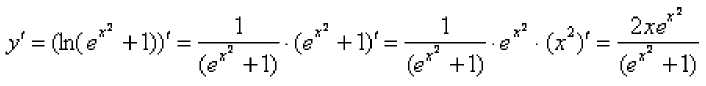
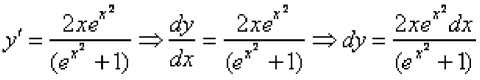
Список литературы Дифференциальные уравнения первого порядка
- Задорожний В.Г. Моментные функции решений стохастических дифференциальных уравнений. Препринт, Воронеж, ВГУ, 1992
- Емелин А. Статья на тему "Дифференциальные уравнения с разделяющимися переменными". 2010 год
- Задорожний В.Г., Смагина Т.Н. Отыскание моментных функций решения задачи Коши для дифференциального уравнения второго порядка// Вестник ф-та ПММ, Воронеж, ВГУ, 1998


