Дифференциальный метод расчёта дифракции рентгеновских лучей на кристалле: скалярная теория

Кристаллы могут быть найдены в природе повсюду. Как правило, мы представляем их себе в виде минералов (драгоценных камней, графита и т.д.), однако примерами кристаллов являются снежинки, лёд и кусочки соли. С древних времен кристаллы интригуют людей своей красотой – симметричной формой и разнообразием цвета, им приписываются магические свойства.

Однако только в начале 20-го века были сделаны открытия, позволившие «увидеть» внутреннюю структуру кристаллов через дифракционную картину рентгеновских лучей.

В 2014 году международное научное сообщество отметило 100-летие кристаллографии [1].

Ещё в 1611 году немецкий математик и астроном Иоганн Кеплер, наблюдая симметричную форму снежинок, озадачился объяснением их внутренней структуры.

Лишь почти 200 лет спустя французский минералог Рене Джюст Гаюи вывел геометрический закон кристаллизации [2], из которого следовала периодичность кристаллической структуры. Закон Гаюи разрешал только 2-, 3-, 4- и 6-кратную симметрию вращения. На основе этих ограничений Мориц Франкен-гейм (в 1826 году) и Иоганн Хессел (в 1830 году) пришли к выводу, что возможны 32 типа кристаллов.

Однако в 1850 году Август Бравэ на основе представлений Людвига Зеебера (в 1824 году) и Габриэля Делафосса (в 1840 году) о кристалле как массиве точек получил только 14 возможных типов решёток [3].

Это противоречие разрешил Леонард Зонке, введя 65 пространственных групп в 1879 году. Через несколько лет русский учёный Евграф Степанович Федоров обобщил этот результат до 230 пространственных групп [4, 5]. Нужно ли было столько групп? Чья концепция правильнее? На эти вопросы удалось ответить только после экспериментальных исследований.

Открытие рентгеновских лучей Вильгельмом Конрадом Рентгеном в 1895, награждённым в 1901 году первой Нобелевской премией по физике, и эксперименты по дифракции рентгеновских лучей на кри- сталлах, проведённые немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912 году, явились основополагающими событиями для развития такой области научных исследований, как кристаллография.

Не менее важным было открытие Уильяма Генри Брэгга и Уильяма Лоуренса Брэгга в 1913, что рентгеновские лучи могут быть использованы для определения положения атомов внутри кристалла и расшифровки его трёхмерной структуры [6–9]. Известное как закон Брэгга, это открытие в значительной степени способствовало современному развитию всех естественных наук, поскольку атомная структура определяет химические и биологические свойства материи, а кристаллическая структура – физические свойства вещества.

Макс фон Лауэ получил Нобелевскую премию по физике в 1914 году, а отец и сын Брэгги были удостоены этой премии в 1915 году. Разработанная ими теория получила название геометрической или кинематической теории.

Кинематическая теория рассеяния была впоследствии дополнена более правильными расчётами интенсивностей и атомных амплитуд с учётом влияния тепловых колебаний, определения фаз структурных амплитуд на основе аномальной дисперсии и других усовершенствований. Большой обзор по истории развития кристаллографии до 70-х годов имеется в монографии З.Г. Пинскера [10].

Характерной чертой кинематической теории является учёт взаимодействия каждого атома только с первичной волной в кристалле. При этом не учитывается многоволновое рассеяние, которое является актуальным при исследовании структуры белковых кристаллов. Также недостатком кинематической теории является пренебрежение законом сохранения энергии, так как энергия проходящей через кристалл первичной волны считается неизменной, хотя часть её сообщается рассеянным волнам.

Глубокий анализ явлений, протекающих при распространении рентгеновских волн в кристаллах, был проведён Эвальдом. Основы динамической теории Эвальда изложены в книге Р. Джеймса [11]. В этой теории кристалл рассматривался как периодическая структура, состоящая из точечных резонаторов, или диполей. Теория Эвальда включала дисперсию падающей волны внутри кристалла и естественный переход к многоволновому рассеянию, что позволило предугадать аномальное прохождение в поглощающих кристаллах; симметричное и асимметричное отражения; отражение по Лауэ; а также основные интерференционные эффекты при рассеянии в идеальных кристаллах.

В конце двадцатых годов Бете по аналогии с динамической теорией рассеяния рентгеновских лучей Эвальда предложил динамическую теорию рассеяния электронов, что послужило открытию дифракции электронов в 1927 г. Аналогичный подход с ясным и кратким объяснением динамического рассеяния рентгеновских лучей рассмотрен в монографии В. Заха-риасена [12]. Последующие формы теории Эвальда получили широкое распространение [13].

Основные различия между кинематической и динамической теорией рассеяния рентгеновских лучей в кристаллах можно свести к двум пунктам: 1) направления и угловая ширина дифрагированных пучков, 2) величины интегрального отражения.

Однако в результате множества экспериментальных исследований было показано [10] лишь небольшое отличие результатов, полученных в рамках динамической теории, от значений углов, предсказываемых кинематической теорией (порядка нескольких угловых секунд). Это привело к мысли о том, что динамическая теория имеет весьма узкую и специальную область применения. Что касается интенсивностей, значения которых различаются в некоторых случаях больше, чем на порядок величин, то и это различие не играет существенной роли, так как имеет место лишь для редчайших экземпляров кристаллов.

В период между 20-ми и 60-ми на основе рентгеновской кристаллографии удалось узнать многое о строении живых организмов, что имело очень важное значение для здравоохранения. Были выяснены структуры множества биологических молекул, включая холестерин, пенициллин, витамин В12 и инсулин. После первых исследований в 1962 году были определены кристаллические структуры 90000 белков, нуклеиновых кислот и других биологических молекул. Одной из самых больших вех 20-го столетия было открытие структуры ДНК на основе дифракционных эффектов. Белковая кристаллография является основным инструментальным средством современных биологической и медицинских наук.

В послевоенный период были достигнуты большие успехи в технологии получения сверхчистых полупроводниковых материалов и в особенности в изготовлении довольно совершенных монокристаллов, таких как Ge, Si и GaAs. Большое практическое значение в квантовой электронике и радиотехнике также приобрели монокристаллы кварца и других веществ. Это послужило новым толчком к развитию методов исследования подобных монокристаллов, в частности, в динамическом рассеянии рентгеновских лучей, как к одному из основных методов исследования и контроля степени совершенства кристаллов.

Важным этапом в разработке динамической теории было рассмотрение случая поглощающего кристалла и вывод формул для коэффициентов и интегральных величин отражения и прохождения. Одним из важнейших эффектов, наблюдаемых при динамическом рассеянии в идеальных кристаллах, является явление аномального прохождения в области максимума. Этот эффект был обнаружен чисто экспериментально и назван эффектом Бормана, по имени автора этих работ [14–16]. Фактически в работе М. Лауэ [17] эффект Бормана показан как очевидный вывод из динамической теории.

Аномальное прохождение рентгеновских лучей в толстом поглощающем кристалле имеет важное принципиальное и практическое значение. В основе динамической теории Эвальда–Лауэ лежит квазиклас-сическое уравнение Максвелла, решением которого является так называемая блоховская волна, которая в двухволновом приближении аппроксимируется двумя плоскими волнами. Эффект Бормана заключается в том, что для одного из полей поглощение резко возрастает, а для другого – резко снижается против нормального, что и приводит для этого поля к аномальному прохождению. Аномальное прохождение одного поля и поглощение другого отражаются в своеобразных формах максимумов прохождения при различных условиях эксперимента.

Интересный и важный класс явлений, обнаруженных сначала экспериментально [18–19], а впоследствии исследованных теоретически Эвальдом и другими авторами [20–22], относится к динамическому рассеянию с учётом нескольких взаимодействующих волн в кристалле. При этом наблюдается заметное изменение характера и величины эффектов аномального прохождения в поглощающих кристаллах.

Существенную роль в рассеянии рентгеновских лучей в кристаллах, в том числе и в динамическом рассеянии, играют тепловые движения атомов, а также диффузное рассеяние, частично также зависящее от тепловых колебаний [23–24].

Динамическая теория рассеяния рентгеновских лучей в кристаллах с дефектами начала разрабатываться с 60-х годов. По аналогии с геометрической оптикой было развито лучевое приближение теории Эвальда– Лауэ и были получены удовлетворительные результаты в построении динамической теории рассеяния в упруго-деформированных кристаллах [25–27]. Более общей и строгой является теория, основанная на уравнениях С. Такаги, выведенных из уравнений Максвелла, в которых волновое поле в кристалле зависит от двух переменных х и z, отвечающих плоскости, образованной векторами преломленной и дифрагированной волн [28–29]. Этот результат можно рассматривать, в частности, как доказательство эквивалентности двух форм динамической теории для иде- ального кристалла: Эвальда–Лауэ и обобщённой. Вместе с тем эта последняя имеет по меньшей мере два существенных преимущества. Прежде всего, она непосредственно позволяет перейти от приближения плоской падающей волны к общему случаю падающего волнового пакета, возбуждающего в кристалле пространственно неоднородное волновое поле [30–31]. Схема построения обобщённой теории применительно к идеальному кристаллу изложена в обзоре [32].

В настоящее время увидеть строение веществ в наномасштабе можно средствами сканирующих туннельных или атомно-силовых микроскопов [33, 34]. Наномасштабные изображения позволяют изучать свойства наноматериалов на основе анализа их атомарной структуры [35]. Трёхмерная кристаллическая решётка является математической моделью, которая не только позволяет описать структуру любого кристаллического вещества, но и определяет его основные физико-химические свойства. Задача структурной идентификации кристаллических решёток по сей день остаётся одной из основных задач рентгеноструктурного анализа [36].

С точки зрения обрабатываемого образца могут быть идентифицированы два метода рентгеновской кристаллографии, а именно: 1) монокристаллической рентгеновской дифракции; 2) порошковой рентгеновской дифракции.

Метод монокристаллической дифракции использует относительно крупные кристаллы и даёт набор разрозненных данных, с помощью которых можно определить структуру. Тем не менее, большинство материалов, используемых в технической сфере, не могут использовать крупные кристаллы, так что приходится прибегать к методу порошковой дифракции с использованием материалов в форме очень небольших кристалликов. Обе технологии хорошо дополняют друг друга, имея свои сильные и слабые стороны и области применения.

Извлечение структурной информации из дифракционной картины представляет собой решение так называемой обратной задачи дифракции в особой постановке. Чтобы её решить, необходимо сначала в рамках той или иной структурной модели кристалла сформулировать прямую задачу дифракции и связать данные измерений с электронной плотностью и параметрами атомного теплового движения.

В данной работе дифракция рентгеновских лучей на идеальном кристалле рассмотрена в рамках скалярной волновой теории. На основе решения уравнения Гельмгольца получены асимптотические выражения, справедливые в случае облучения кристалла жёстким рентгеновским излучением. Данная работа является первой из серии планируемых публикаций, посвящённых анализу дифракции рентгеновских лучей в рамках электромагнитной теории.

• 1.    Приближение однократного рассеяния

В рамках скалярной теории распространение излучения в декартовой системе координат описывается уравнением [33]:

d ²W ( x , y , z ) d ² W ( x , y , z ) d ² W ( x , y , z ) d x ²             d y ²             d z ²              (1)

+k 2e( x, y, z) W (x, y, z) = 0, где e(x,y,z) = 1 + 4n%(x,y,z),                          (2)

X ( x , y , z ) - пропорциональна электронной плотности, мала по сравнению с единицей.

С учётом (2) перепишем (1), опустив координатную зависимость, в виде:

V2W + k2W = -4nk2xW.(3)

Решение (3) представим в виде суммы падающего и рассеянного поля

W = E0 + E .(4)

Падающее поле удовлетворяет однородному уравнению Гельмгольца

V2 Eо + k2 Eо = 0,(5)

а рассеянное поле удовлетворяет неоднородному уравнению Гельмгольца

V2E + k2E = -4лk2xE0.(6)

Таким образом, вместо (4) получим уравнение

V2 E0 + k2 E0 +V2 E + k2 E = -4n k 2%E0.(7)

Обозначим

p(x,y,z) = k2x(x,y,z)E0 (x,y,z),(8)

тогда из (6) получаем:

V2 E + k2 E = -4np.(9)

Решение (9) имеет вид:

E(x,y,z)=[ p(^,n,o)exp('kR)d^dndo ,(10)

-^

где R = V(x-^)2 + (y-n)2 + (z-o)2 .(11)

• 1.1.    Представление поля в дальней зоне

Пусть электронная плотность имеет вид

p(^,n,o)= ^ pnmi exp [ i (n a1 + mb +1c )rc ],(12)

n,m,l где a1, b1, c1 – вектора обратной решётки кристалла, rc =^ex +ney +oez - вектор произвольной точки внутри кристалла.

Пусть плоская волна падает на структуру с распределением электронной плотности (12). Согласно принципу Гюйгенса–Френеля каждая точка электронного облака излучает сферическую волну с амплитудой, пропорциональной плотности электронного облака, и начальной фазой, равной фазе падающей плоской волны:

E ( x , y , z ) = J p ( ^,n,o ) x

^V                     ( ikR )              ⁽¹³⁾

x exp [ ik ( « 0 ^ + Р 0 П + Y 0 0 ) ] —^R —- d^ d n d o .

Интегрирование производится по всему объёму кристалла.

После известных преобразований выражение в дальней зоне приобретает следующий вид:

E (x, y, z ) =

exp⁽ ikR o ) _x R 0

x j p ( ^,n,o ) exp ( ik ( a o ^+P o B + Y o o ) ) x

x exp ( ( - ik / R _o) ( x ^ + y n + z o ) ) d ^ d n d o ,

2. Приближение многократного рассеяния

В рамках многократного рассеяния дифракция рентгеновских лучей также описывается уравнением Гельмгольца (1). Запишем его в декартовой системе координат ( x 1 , x ² , x 3 ):

где R ₀ = 4x 2 + У 2 + z 2 .

• 1.2.    Представление решения в точках обратной решётки

Преобразуем выражение для амплитуды дифрагированного света в виде

E(a-ao) = ехр(kR ' |p(^n,o)x

^R 0      ^V                              (15)

x exp{-ik [(a-ao) ^+ (P-Po)n + (Y"Yo)o]} d^ dn do, где (a,P, y) =

xyz R 0 , R 0 , R 0

d2W (x 1, x2, x3) d2W (x 1, x2, x3) d( x1 )2     +     d( x2 )2     + d2W (x 1, x2, x3) +     d( x3 )2

+

+ k ²e( x 1 , x ² , x ³ ) W ( x 1 , x ² , x ³ ) = o.

В пространственно-частотном представлении:

W ^[ x 1 , x ² , x ^{3 ]} = I" E ^[a 1 ,a ₂ , x ^{3 ]} x

^{1 У У У}                         (22)

x exp I ik [ a 1 x ¹ + a ₂ x ² II d a 1 d a ₂,

Из (15) очевидно, что амплитуда есть Фурье-преобразование от плотности электронного облака в рассматриваемой системе

_ < 1    2    3

e I x , x , x

_             3

a1,a2, x3

e a - «. ) = ^{exp (} i ^kR o ¹ x

⁰         R 0

[                    зЗ)

x exp \ ik I a 1 x +a ₂ x II d a 1 d a ₂.

xJ p(^,n,o)exp [-ik(a - ao)rc|d^dndo.

Интегрирование по всему объёму кристалла заменим интегрированием по элементарной ячейке V_e :

rc = re + n a + m b +1c , где a,b,c – вектора кристаллической решётки.

E(a-ao)= ^p'kRo) Z Jp(^n,o)x

R0      n,m,l Ve x exp [-ik (a - ao)(re + n a + mb +1 c) ] d^ dn do.

Пусть теперь точки наблюдения находятся в точках обратной решётки a - ao = pa1 + 5b1 + qc1.                           (19)

Амплитуда рассеянного сигнала в точках (19) бу-

дет равна:

E psq

exp( ikR ₀ ) R 0

^[ Z 1 ] x

| n , m , 1 у

x J p ( ^,n,o ) exp [- ik ( a - a o ) Г е ] d ^ d n d o =

^V e                                                        (20)

exp( ikR )[^Jf ,, x

= ——"I Z 1IJp(^n,o)x

^R o       у n , m , 1 у у

x exp [- ik ( p a 1 + 5 b 1 + q c 1 ) r e J d ^ d n d o .

Выражение ( Z 1) означает, что интенсивность n , m , l

пропорциональна количеству элементарных ячеек. Анализируя выражение (20), видим, что амплитуда рассеянного сигнала в определённой точке обратной решётки есть соответствующий коэффициент в разложении ряда Фурье электронной плотности.

Подставляя эти выражения, получаем уравнение (21) в пространственно-частотном представлении:

- k ² [ ( a 1 )² + ( a ₂ )² ] E ( a 1 , a ₂ , x ³) +

d ² E ( a 1 ,a ₂ , x ³) ⁺      d ( x ³) 2

+

+ k ²    e ( a 1 -® 1 ,a ₂ -® ₂ , x 3 ) x

-^

x E ( to 1 ,to ₂ , x ³)d to 1 d to ₂ = o.

Рассмотрим частный случай кристаллического тела. В случае монокристалла диэлектрическая проницаемость представляется следующим образом

[ 1    2    3 )

e I x , x , x I =

= Z en1 n2n3 exp[i(n1B1 + n2B2 + n3B3) RJ, n1,n2,n3

где B 1 , B ₂ , B ₃ - вектора обратной решётки в произвольной системе координат,

R = x 1 e 1 + x ²e ₂ + x ³ e ₃.                               (26)

Поперечные вектора в ортогональной декартовой системе имеют вид:

r = ( R 1 , R 2 , o), b i = ( b_n , b i 2 , o), a = ( a ! ,a 2 , o).

Представим выражение для диэлектрической про-

ницаемости в виде:

e ( x ¹ , x ² , x ³) =

= Z e n ¹ ” ² ” ³ ( x ³ ) exp [ i ( n ₁ b ₁ + n ₂ b ₂ + n ₃ b ₃ ) r J , n ₁, n ₂, n ₃

где e n1”2 n 3 (x3) =

= e ” 1 ” ² ” ³ exp [ i ( n 1 b ₁₃ + n ₂ b ₂₃ + n ₃ b ₃₃) x ³ ] .

Из (23) и (27) с точностью до коэффициента имеем:

f_. _. 3 e I a,a2, x

7- f* pf 1 2 37

I — I e I x , x , x I x

7 J —* V              7

x exp [— ik f a₁ x ¹ + a₂ x ² 7 ] d x ¹ d x ² —

k ²

e l a,,a₇, x I — —_Tx

^{V 12 7} 4 n ²

— f Z ^{e n i}n ² n ³ ( x ³ ) exP [ i ( n 1 b 1 + n 2 b 2 + n 3 b 3 ) ^r ]x ⁿ1 , n 2 , ⁿ 3

x exp [— ik f a₁ x ¹ + a₂ x ² 7 ] d x 1 d x ² —

— Z enn2n3 (x3 )x n1 ,n2 ,n3

Г *      J bi      b2 b3     I x exp ik\n, + n2 + n, a I r f I 1 k 2 k 3 k I

d r .

Из вышеприведённых выкладок следует, что

Г* ^{e f a} i

— ®_pa₂ — ®₂, x ³ 7 E f ®_p®₂, x ³ 7 d ro —

— E Z e n ⁿ ■ ^{n 3} ( x ‘ ) S n ₁ , n ₂ , n ₃

. f b, b Ьз 7 a — ro — n. — + n , — + n —

V ¹ k ² k ³ k 7

— Z e nn 2 ⁿ 3 ( x ³ ) Z E mm 2 ^m 3 ( x ³ ) 5 n ₁, n ₂, n ₃                      m ₁, m ₂, m ₃

x Z e n ⁿ 2 ⁿ 3 ( x ³ ) 5

n ₁ , n ₂ , n ₃

f b, b, b, 7

a — n, — + n, —— + n, —

V ¹ k ² k ³ k 7

Пусть поле в пространственно-частотном пред-

ставлении имеет вид

EVtopto2,x37 — Z Emm2m3 (x3)x m1 ,m2 ,m3

x5

f          b.       b, b₃ 7

ro — a_n + m, — + m , — + m. —

V 0 ¹ k ² k ³ k 7

Тогда интегральное слагаемое в (24) можно запи-

сать в виде:

Z E mm ² m ³ ( x ³ ) 5

m ₁ , m ₂ , m ₃

. f b, b a — n. — + n, — + n,

V ¹ k ² k ³

( . b, b. Ьз ro — an + m. — + m, — + m. —

V 0     ¹ k ² k ³ k

b₃ 7 f b, b     b 7

— — a„ + m. — + m, — + m, — k 7 V 0 1 k 2 k 3 k 7

— Z Z E m¹" ^{2 m 3} ( x ³ ) e nn ² n ³ exp [ i ( n 1 b₁₃ + n ₂ b ₂₃ + n ₃ b 33 ) x ³ ] 5 j a — m 1 , m 2 , m 3 n 1 , n 2 , n 3                                                                                                        (

— Z Z E

m ₁ m ₂ m ₃

m ₁, m ₂, m ₃ p ₁, p ₂, p ₃

( x ³ ) e p 1 ^{— m} 1 , p 2 ^{— m} 2 , p 3 ^{— m} 3

x

^x exp { i [ ( P 1 ^{— m} 1 ) ^b 13 ⁺ ( P 2 ^{— m} 2 ) ^b 23 ⁺ ( P 3 ^{— m} 3 ) ^b 33 ] ^{x 3} } ⁵ 1 ^{a —}

Подставляя выражение для поля и диэлектрической проницаемости в пространственно-частотном

представлении в интегральное уравнение, получим систему обыкновенных дифференциальных уравнений для E ^{p 1 p 2 p 3}( x ³):

f          b,       b₂      b₃ 7 2

— k a_n + p, — + p-, — + p₃ — x

V ^{0 1} k ² k ³ k 7

j ² pP 1 , p 2, p 3 /„7

x E^p' ■ ^{p 2}, ^{p 3} ( x ³) + d--------- + d( x ³)²

d ro —

^a 0 ⁺ ( m 1 ⁺ n 1 ) -b - 1- + ( m 2 ⁺ n 2 ) b k ². ⁺ ( m 3 ⁺ n 3 ) J k L

bbb a0 + P1V + P2 V + P3 73 kkk

3. Теория возмущений для решения системы уравнений

Матрицу (32) системы дифференциальных уравнений можно представить в виде

p ₁ p ₂ p ₃         p ₁ p ₂ p ₃              p ₁ p ₂ p ₃

^m 1 m 2 m 3      ^m 1 m 2 m 3      ⁿ m ^ 2 m 3 ^.

Пусть теперь поле внутри кристаллической решётки представляется в виде суммы падающего поля и поля, рассеянного кристаллической решёткой:

+ k ² Z e P 1 ^{— m} 1 , p 2 ^— m 2 , p 3 ^— m 3 ( x ³) E ^m 1 ’ ^m 2 , ^m 3 ( x ³) _— 0 m

E P 1 P 2 P 3 _— E^P' P 2 P 3 + E^p' p 2 p 3

Выражение (31) можно переписать в более ком-

пактном виде:

d 2 E p ₁ p ₂ p ₃ d( x ³)²

2     p ₁ p ₂ p ₃    m ₁ m ₂ m ₃

" 1 m 2 m 3

— 0,

Подставляя это представление для поля в систему дифференциальных уравнений (32), получаем:

J 2 f CP1P 2 P 3 . p^pl P 2 P 3 7

u !E 0     + Es\

------------------2+

d(x3)2(36)

где

H "m"" 3 —e ^{P 1 —} m ¹, ^{P 2 —} m ^{2 , P 3 —} m ³ exp { i [ ( P 1 — " 1 ) b 13 +

ik 2 I TP 1 P 2 P 3 ./I TT-A P 1 P 2 P 3 ^7f /7 " 1 ^m 2 ^m 3

⁺ k V I m 1 m 2 m 3 ^{+ 4 ПП} " 1 m 2 m 3 J ^ E 0

+ E m ^m 2 ^m 3

7 — 0.

⁺ ( P 2 ^— m 2 ) ^b 23 ⁺( P 3 ^— m 3 ) ^b 33 ] x 3 } ^—

X P 1 X P 2 X P 3 -L n ^b1 -I- n ^b2 -I- n ^b3    _

^—5 m, ⁵ m ⁵ m, ^a 0 ^{+ P} 1 7" ^{+ P} 2    ^{+ P} 3 7"   ^—

¹ L k k k _

— 5 ^p' 5 ^p 2 5 ^{p 3} J 1 — ^[ a₀ + p .b¹ + p ₂b² + p ₃b³ 1 + mm 2 m 3 1   l ^{0 P 1} k ^{P 2} k  ^{P 3} k ]

После раскрытия скобок и пренебрегая слагаемым

4 n k ²A mpXm_m ^E "^{m 2 m 3} , получим:

2 p ₁ p ₂ p ₃       2 p ₁ p ₂ p ₃

0                  s             2 p ₁ p ₂ p ₃ m ₁ m ₂ m ₃

^{+          +№} I m,™,™, E 0     ⁺

d( x ³)²      d( x ³)^{2          m 1 m 2 m 3 0}

+ k 2 / P 1 P 2 p 3 E "^m 2 ^m 3 + 4 n k 2 A P 1 p 2 p 3 E "^m 2 ^m 3 m ₁ m ₂ m ₃ s                    m ₁ m ₂ m ₃ 0

— 0.

+ 4 nX ^{p —} m , ^{p 2 —} m ², ^p 3 ^— m 3 x exp { i [ ( p ₁ — m ₁ ) b ₁₃ + ⁺( P 2 ^{— m} 2 ) ^b 23 ⁺( P 3 ^{— m} 3 ) ^b 33 ] ^x 3 } .

Полагая, что диэлектрическая проницаемость приблизительно равна единице, и учитывая малость амплитуды рассеянной волны по сравнению с падающей, запишем отдельно для каждой составляющей поля:

<

d 2 E ₀ p 1 p 2 p 3

d 2 E p ₁ p ₂ p ₃

,2 (, (       Ь,     Ьb'

+ k 1 - I 0) + p^ + p 2^2 + p 3-3 V       k      kk

X E "^{2 p 3} = 0,

12 С Г         b1      b2

+ k 1 —I ao + Р1"Т + p 2 у + p зу l        k      kk

V

2 ^

I X

2 I

I X

p 1 p 2 p 3              2 p 1 p 2 p 3 m 1 m 2 m 3

s                     m ₁ m ₂ m ₃ 0

где p1 p2p3 _ yp1— m1,p2 — m2,p3 — m3 X

W 1 m 2 m 3     ^x

X exp { i [ ( p 1 — m 1 ) b 13 + ( p 2 — m 2 ) b 23 + ( p 3

-

m ₃ ) b₃₃ J x ³ } .

Решение первого уравнения в (37) имеет вид:

E _o ^p i ^p 2 ^p 3 = A^p 2 ^p 3 X (

X exp ik 11

^^^^^^e

bbb

« 0 ⁺ p i ^{1 +} p 2 ^{2 +} p 3 ³

kkk

7 A

I x³

.

V

В случае, если падает плоская волна, то

EO00 = SpSp2Sp3 x f                       ( I--------------------------------------------------------- x< A0 p p2p3 exp ik 11

^^^^^^^

bbb a0+ pi 7"+ p 27-+ p 37-kkk

V

.2 1

I x³

+

+ A 0 ^{p p 2 p 3} exp

V

—

(         b,      b₂      b₃ 1 ^{2 1}

■ Ik I ^a 0 ⁺ p 1T ⁺ p 2T" ⁺ p3-Г I

I k k k ) 7

x ³

x 3 .

Тогда уравнение для рассеянной волны имеет вид: d 2 E p ₁ p ₂ p ₃ ^s

+ k ² 1

V

^^^^^^e

b      b      bl I a0 + p1T + p2~Г + p3~Г I IX k      k      k 7

X E pp ^{2 p 3} =— 4 n k ² A ^p 00^{2 p 3} E ₀⁰⁰⁰.

Для того, чтобы в выбранном направлении происходило усиление волн, необходимо выполнение условия:

[« 03 + ( p 1 b 13 + p 2 b 23 + p 3 b- ) J ² =

. (    . b . b, . b I2

= ^{1 —} I ^a 0 ⁺ p 1 1 ⁺ p 2 2 ⁺ p 3 ³ | ,

V k k k 7

из которого можно получить окончательное условие:

BBB a0 + ^171 + p 2T2 + p 372 || = 1.           (42)

• V V k k k J 7

• 4. Моделирование дифракции
  
  для базовых типов кристаллических решёток

Это уравнение представляет собой известное в кристаллографии уравнение Лауэ, которое определяет направление на максимумы дифракционной картины. В данном разделе это уравнение было получено на основе решения уравнения Гельмгольца, что не является классическим подходом. Развитый метод ориентирован на использование высокопроизводительных вычислительных средств.

При рентгенографических методах исследования строения твёрдых тел применяется жёсткое рентгеновское излучение с длинами волн от 0,2 Å до 2,5 Å. Для анализа монокристаллов, как правило, используют излучения с непрерывным спектром.

В данном разделе рассмотрено моделирование дифракции рентгеновского излучения на монокристаллах с базовыми типами решёток (рис. 1) при различных соотношениях длины волны излучения и расстояниями между атомами (размеры рёбер решёток).

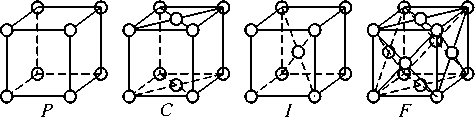
Рис. 1. Типы решёток: примитивная (P), базоцентрированная (C), объёмоцентрированная (I), гранецентрированная (F)

Для примитивной решётки в декартовой системе координат: вектора равны a =(1, 0, 0), b =(0, 1, 0), с =(0,0, 1), вектора обратной решётки равны a 1 =(1, 0, 0), b 1 =(0, 1, 0), с 1 =(0, 0, 1).

Для объёмоцентрированной решётки вектора равны a =(1, 1, 0), b =(0, 1, 1), с =(1, 0, 1), вектора обратной решётки равны a 1 =(1, 1, –1), b 1 =(–1, 1, 1), с 1 =(1, –1, 1).

Для гранецентрированной решётки вектора равны a =(1, 1, –1), b =(–1, 1, 1), с =(1, –1, 1), вектора обратной решётки равны: a 1 =(1, 1, 0), b 1 =(0, 1, 1), с 1 =(1, 0, 1).

Моделирование выполнялось для плоской волны, распространяющейся вдоль оси Z , с диапазоном приведённых длин волн Ze [ A min / a , A max / a ], где a - расстояние между узлами кристаллической решётки.

На рис. 2 показаны результаты моделирования для рассматриваемых трёх типов решёток для %е [0,2,0,25]. В первом столбце приведены картины распределения возможных максимумов, вычисленных из условия Лауэ (42), а во втором столбце – с уменьшенным в 10 раз диапазоном приведённых длин волн. Картины представляют собой плоские проекции с полусферы единичных направлений с максимальным углом θ max с осью z , близким к 90 градусам.

Как видно из приведённых на рис. 2 результатов, картина дифракции существенно зависит от структуры элементарной ячейки кристалла. Сужение диапазона длин позволяет выделять только определённые дифракционные порядки из возможного набора максимумов.

В табл. 1 приведены результаты моделирования для рассматриваемых трёх типов решёток с различными диапазонами приведённых длин волн.

Как видно из результатов расчётов, увеличение относительной длины волны рентгеновского излучения приводит к увеличению радиуса концентрации дифракционных порядков на полусфере регистрации. Если длина волны слишком мала по сравнению с расстояниями между атомами, то картина дифракции становится очень сложной. Поэтому оптимальным для анализа считается излучение, длины волн которого составляют от единиц до десятых долей межатомных расстояний.

al)

б1)

a2)

б2)

в2)

в1)

Рис. 2. Результаты моделирования для примитивной (а), объёмоцентрированн^й (б) и гранецентрированной (в)

решёток для хе [0,2, 0,25]: картины распределения максимумов Лауэ (42) (первая строка) и с уменьшенным диапазоном длин волн (вторая строка)

Табл. 1. Моделирование для примитивной, объёмоцентрированной и гранецентрированной решёток для различных диапазонов длин волн (картины распределения дифракционных порядков)

Диапазоны приведённых длин волн и область обзора	Примитивная	Объёмоцентрированная	Гранецентрированная
ζ ∈ [0,9, 1,1], sin θ max = 0,999
ζ ∈ [0,5, 0,55], sin θ max = 0,999
ζ ∈ [0,05, 0,0503], sin θ max = 0,2
ζ ∈ [0,05, 0,0503], sin θ max = 0,4			д!(:1

Заключение

В данной работе приведён обзор основных исторических экспериментальных и теоретических разработок в области рентгеноструктурного анализа, позволяющий получить представление о перспективных направлениях дальнейшего развития.

В основной части рассмотрен дифференциальный подход решения задачи дифракции рентгеновских лучей в рамках скалярной теории. На основе этого подхода были получены классические формулы Лауэ, используемые в рентгеноструктурном анализе кристаллов. В дальнейшем разработанный подход можно применить для получения приближённых решений задачи дифракции. Развитый метод ориентирован на использование высокопроизводительных вычислительных средств.

Примеры численного моделирования для базовых типов кристаллических решёток иллюстрируют раз- личие в дифракционных картинах и позволяют понять стратегию выбора диапазона длин волн рентгеновского излучения.

Приложения

A. Вычисление коэффициентов ряда Фурье

Пусть электронная плотность имеет вид

p ( r ) = 2 P nml exp ( i ( n a ₁ + m b ₁ + l c ₁ ) r ) .           (А1)

Для того, чтобы найти коэффициенты этого ряда, умножим это выражение на exp( - i (p a ₁ + s b ₁ + qc1) r ) и проинтегрируем по объёму элементарной ячейки:

J p ( r ) exp ( - i ( p a ₁ + s b ₁ + q c 1 ) r ) d³ r =

V E

= ^ р nml J V exp [ i ( ( n - p ) a ₁ + ( m - s ) b + + ( l - q ) c ₁ ) r ] d³ r .

Далее, вычисляя интеграл

(А2)

J exp ^[ i ^f ( n - p ) a, + ( m - s ) b + ( l - q ) q ) r J d³ r =

^V E                                                  (А3)

= Ve 5 p 5 m 5 q, получаем:

p ^psq =      „ p ( r ) exp ( ^- i ( p a i + s b i + qc i ) r ) d³ r . ^(А4)

V E ^VE

Б. Решение дифференциального уравнения второго порядка с постоянными коэффициентами

Пусть дано дифференциальное уравнение a^-y + b— + cy = f(x\ .(Б1)

dx2d

Представим решение в виде

У (x) = ci (x)У1 (x) + c2 (x)У2 (x) ,

где y ₁ ( x ) , y ₂ ( x ) - решения однородного уравнения. После подстановки выражения (Б2) в (Б1) и преобразования получим:

f d² c.       , d c . d y, d² c,       , d c , d y-, 1

a l —2- y ₁ + 2 ^{1 Z1} + — 22- y ₂ + 2— 2^-2 I +

I dx        dx dx dx        dx dx J

dc      dc2 1    I d2yt    dyt y1 +    y 21 + c1 a + b dx      dx I dx2     dx

d c

d x

a

d² c.       d c . d y. d² c₂       d c ₂ d y ₂1

—Ty ₁ + — ¹— + —T y 2 + —2~ I + d x      d x d x d x      d x d x J

+1 d c _Ld y _L + d c 2 d y 2 I d x d x d x d x

+

d c     d c₂ ¹ л

— y 1 + — y 2 I = ^f ( x ) , d x      d x I

d ^f d c. d c, ¹ ( d c . d y. d c , d y, — I — ¹ y ₁ + — ²y ₂ I +1 — + —²^-² dx | d x d x J | d x d x d x d x

d c     d c   ¹

-?■ y 1 ⁺ "T2 у 2 | = ^f ( ^x ) .

d x     d x   I

d c

I

⁺ cy 1 +

V

(Б3)

(Б6)

(Б7)

Пусть теперь функции c ₁ ( x ) , c ₂ ( x ) удовлетворяют

уравнению f dc.      d c2

I— У 1 + — ²

I d x      d x

(Б8)

Тогда исходное уравнение (Б1) сводится к следующему:

f d c. dy, a I —¹¹

I d x d x

d c ₂ d y ₂ d x d x

¹ = ^{f ( x} ) .

(Б9)

Тогда для определения функций получим систему уравнений

d c     d c

У 1^ ⁺ У 2 a = 0, d x     d x

d y , d ^c! d y ₂ d ^c ₂ ^{f (} x ) 1=

. d x d x d x d x     a

(Б10)

'       2 ,

^{+ c} 2 a—² + b—² + ^cy 2 = ^{f (} x ) .

( d x      d x

V

Учитывая, что a dy- + b— + cy = 0 , dx2     dx     i выражение (Б3) можно упростить f d2c. , dc. dy d2c2 , al y + 2 1 Z1 +     y 2 + 2

| d x ²       d x d x d x ²

, ^f d c.        d c₂ ¹ z x

⁺ b l— У 1 + — y 2 I = ^f ( x ) . I d x       d x    I

(Б4)

d x d x

d y ^ I +

(Б5)

Представим уравнение (Б5) в виде

которую запишем в матричном виде:

	I y1 d У 1 I d x	У 2 1 d y 2 d x J	। d c 1 d x d c 2 I d x	=	f 0 1
					f ( x ) I a J	.                       <Б11>
Систе ^ 1 = A 2 = В рез d c 1 d x dc^ = d x		му (Б10) ре 0      y 2 f ( x )   d y 2 a    d x y 1       0 d У 1 f ( x ) d x    a ультате пол - У 2 f ( x ) a A ( x ) y 1 f ( x ) a A ( x )		шаем методом Крамера _ У 2 f ( x ) = - a ’ (Б12) У 1 f ( x ) a . учаем (Б13)
y 1     y 2 где A ( x ) = dy ^ d y 2 d x d x Общее решение и				d y = y^— d x меет вид		d y y 21 . d x

( \ I x - Ут ( t ) f ( t )d t I / \

У(x) = l ai +J0------IУ1 (x) +

( J0     a A(t)     )

I      r x y i ⁽ t ) f ⁽ t ^)d t I _w

• ⁺ 1 a 2 ⁺ J o     a A ( t )     ) y ^{2 (} x ) ^.

Пример dy

• - 4 + toy = f (x).

d x

В этом случае

[ У1 (x) = exp (i ®x),[y2 (x) = exp(-itox).

Общее решение имеет вид

• У    (x) = —1— x

• ^V    ’ -2 i to

  x

  
  

(a1 - J0 exp(-ito(t - x)) f (t) dt) +

(Б14)

(Б15)

(Б16)

(Б17)

+ (a2 + Jox exp (ito(t - x)) f (t) dt) .

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации.