Диффузионный механизм окисления никеля в проводящем канале переключательной структуры Pt/NiO/Pt

Ячейка резистивной памяти (ReRAM) Pt/NiO/Pt представляет собой обычную металл – оксид – металл (МОМ) конденсаторную структуру, характеризующуюся свойствами переключения (рис. 1) из высокоомного состояния «OFF» в низкоомное «ON» (SET) и наоборот (RESET) (рис. 2). Для реализации этого эффекта необходимо провести процесс предварительной электрической формовки (forming), который представляет собой диэлектрический пробой (резкое, скачкообразное изменение проводимости оксидного слоя) МОМ-структур при ограничении проходящего тока. Результатом формовки является формирование наноразмерного канала, структура и химический состав которого отличаются от исходного оксида [7], [12]. Отметим, что образование такого канала подтверждается исследованием переключения в многочисленных экспериментах как в оксидных планарных [3], так и сэндвич-структурах [4], [6], [7], [10], [11], [12], [13], [16].

Несмотря на то что накоплено большое количество экспериментальных данных по изучению эффекта переключения в различных оксидных сис-

темах со шнурованием тока, его механизм до сих пор остается не ясным. Для структуры с оксидом никеля, где состояние «ON» характеризуется наличием тонкого проводящего канала с избытком металла в виде множества фрагментов [13], наиболее устоявшимся предположением о механизме перехода RESET является окисление никеля за счет избытка кислорода в окружающем NiO при высокой температуре, обусловленной джоулевым нагревом [6], [10], [16].

Однако оценка этого нагрева и процесса окисления делается по упрощенным моделям передачи тепла и зависящей только от температуры скорости уменьшения радиуса канала (линейный рост слоя окисления) [10].

В то же время при плотном слое окисла может осуществляться диффузионный механизм окисления, когда в плоской геометрии скорость роста окисного слоя обратно пропорциональна его толщине [8]. В нашем случае этот процесс осложняется цилиндрической геометрией канала и диффузионным механизмом переноса кислорода в окружающем NiO. Возможны три варианта

Формовка

О - вакансии никеля

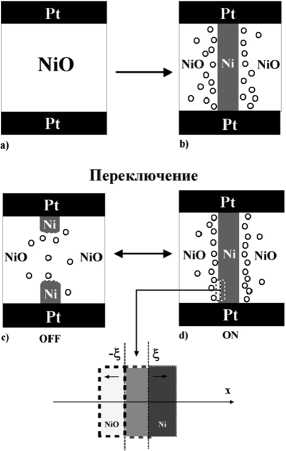
Рис. 1. Схема процессов электрической формовки и переключения МОМ-структуры Pt/NiO/Pt. Внизу показаны границы окисления ( £ ) и ухода никелевых вакансий (- £ ) в плоском случае геометрии канала

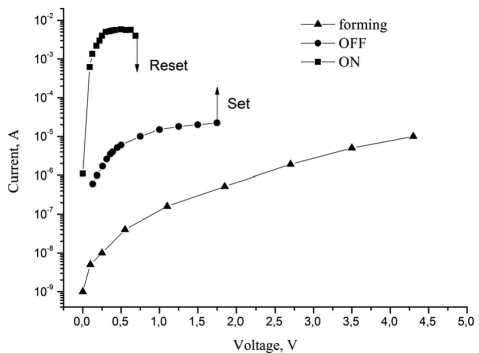
Рис. 2. ВАХ процессов электрической формовки и переключения МОМ-структуры Pt/NiO/Pt

диффузии, приводящие к исчезновению металлической проводимости канала: непосредственная диффузия кислорода в канал, диффузия никелевых вакансий в канал и обратная диффузия атомов никеля из канала.

По данным [5], [9], наибольший коэффициент диффузии в монокристалле NiO (на 2–3 порядка) при характерных температурах разогрева канала ~ 1000 K [11] имеет диффузия никелевых вакансий:

D

vac

Ni

= 1,9 - 10 ² - exp

34540 А

RT J ,

D_№ = 1,5 -10 2 - exp

58000 А RT ) ,

D O = 6,2 - 10 ⁴ - exp

57500 а RT

где D Ni^vac , D Ni и D O – коэффициенты диффузии (cm²/s) никелевых вакансий, никеля и кислорода соответственно, R – универсальная газовая постоянная (cal - K^-1).

Еще выше диффузия никелевых вакансий осуществляется по граням поликристалла [5]:

П vac Л Ш- 2      ( 28200 А

^DNiGB 1,^{0 - 10 -} exp !

, _{п 1П}-₂     ( 14200 А

= 1,0 - 10 - exp I---—

,

= D - коэффициент диффузии по граням

vac где D_NiGB (cm²/s).

Сильная экспоненциальная зависимость коэффициента диффузии от температуры в (1) обуславливает пороговый характер окисления (растворения) канала от уровня тока.

Рассмотрим диффузионный механизм окисления при тонком (плоском) слое окисла. В данном процессе имеются две движущиеся границы: граница окисления, двигающаяся вглубь канала, и граница ухода никелевых вакансий из NiO. Так как процесс окисления лимитируется процессом ухода кислорода из прилегающей к каналу области NiO, то концентрация избытка кислорода в этой области соответствует концентрации его недостатка в канале. Тогда можно считать, что скорости обеих подвижных границ близки, но противоположны по знаку.

Диффузионный поток вакансий nv ( n и v – концентрация и скорость никелевых вакансий) описывается выражением:

nv = - D I n ,                (2)

Ix где координату будем отсчитывать от первоначальной границы канала. Уравнение непрерывности при отсутствии химических реакций внутри NiO есть:

— + div ( nv ) = 0. (3) I 1

Подставляя (2) в (3), получим диффузионное уравнение:

I n = d 1 ² n 1 1        I x ²

Пусть ξ – координата границы окисления, (_ξ) – координата границы ухода вакансий из NiO (см. рис. 1). Тогда граничные условия уравнения (4) есть n(x > ξ) = 0, n(x ≤ –ξ) = no, то есть вакан- сии отсутствуют внутри канала, а их концентрация равна равновесному значению no в глубине NiO до их границы ухода в канал. Аналитическим решением уравнения (4) является [14]:

X + ^ A

2 V Dt _?

n = n ₀ - C - F

где

z

F ( z ) _ —= • e z dz - функция ошибок.

X 7T

N ^П 0

Решение (5) показывает, что концентрация не меняется при пропорциональности координат

корню от времени.

Положим 6 = a/t, тогда d6 _ a1 ~dt ” 26’

где α – коэффициент пропорциональности, а постоянная С в (5), определяемая условием n ( ξ ) = 0, есть

C _

no

F( a / ^)^.

отсутствуют даже при постоянной концентрации на поверхности. В задачах теплопроводности имеется приближенное решение для замерзания (или оттаивания) полого цилиндра изнутри с постоянной температурой на внутренней поверхности [1], [2]. В качестве аппроксимации предлагаются квазистационарные решения, когда для распределения по координате используется стационарное решение, а зависимость от времени определяется движением границы замерзания.

Применим этот метод для задачи окисления цилиндрического канала. Пусть r _o – начальный радиус канала, ξ – радиус поверхности окисления, r vac – радиус границы ухода вакансий из NiO, а n ( ξ ) = 0 и n ( r vac ) = n o . Отметим, что для сохранения потока должно выполняться условие [1]

Для определения α используем условие на границе окисления:

d6   rnn и — _ - D— dt dx ’

222 vac o . Решением стационарного уравнения

которое является следствием (2) при учете того, что недостаток кислорода в канале равен его избытку в окружающем NiO.

Подставляя (5) и (6) в (7), получим трансцендентное уравнение α от D :

d ² n 1 d n

— +_ 0 dr2 r dr будет функция

a

D

2 exp

a

D

n ,rJ a

Ф

I VD

.

Решением (8) является значение a _ 0,80 • VD, тогда 6_ 0,80VD7 и d6 _ 0,32 • D, dt 6

а для времени перекрытия окислом заданной тол-

щины r _o имеем

t o _ 1,56 D .

Отметим, что при фиксированном значении концентрации на начальной границе n (0, t ) = n o аналогичное рассмотрение дает

d6 _ 0,769 • D _ 0,62 • dt 6

t_o = 0,65 • -^ . oD

Последние значения совпадают с решениями задачи замерзания воды при постоянной температуре на поверхности [2].

В цилиндрической геометрии аналитические решения уравнения

^d ² n

dn „     .

— _ D • —- + -•

1 d n

n ( r ) = n o •

ln I §

,

d t

d r r

r d r

с граничными условиями, соответствующими окислению цилиндра с наружной поверхности,

In vac^

16 J

а движение внутренней границы определяется условием окисления:

d6      dn n„ — _ - D-- dt       d r

.

r =6

Тогда для скорости окисления с учетом (11) получим:

d 6 dt

D

6- ln r vac-

2 D

6' ln 66 т -1

.

Интегрируя (15) по ξ от r _o до 0, получим время полного окисления канала:

to _ — • r ² _ 0,347 • r ². o 2 D o         D

Можно ожидать, что квазистационарное приближение дает завышенное значение (16), так как для установления стационарного состояния (13) требуется дополнительное время.

Подтверждение этому можно получить, переходя в (15) к предельному значению £^ r o :

6 In —

rvac - 6) = 2 '(r0 - 6) ,

что соответствует плоской геометрии. В этом

случае

d 6 dt

0.5 • D

( r - ^{6 )}’

в то время как точное решение (10) для плоского слоя равно d^   0,32 - D dt "     §   ’

где ξ соответствует в цилиндре значению ( r o – ξ ). Для уточнения значений (15) и (16) нами про-

изведено численное решение нестационарного уравнения (10). Введем безразмерные перемен-

ные:

n n =— no

'=  ,   = ^ , rr oo

D

T = r?. 2

.

Тогда уравнение (10) и условие (14) запишутся

в виде

d n' _ d² n' 1 d n'

IT az"⁺7 'T⁷ ’

(10 ’ )

< = _dn dT     dr' r .=?

(14 ’ )

Начальные условия задаются как n' = 0 при 0 <  r< 1 и n ' = 1 при r' >  1. Расчет производился методом конечных разностей на счетной области 0 <  г ' <  V2 с выполнением условия устойчивости А т <  (Аг ' )²/2. На границе окисления концентрация обнулялась, а избыток накапливался до значения An' = 1. После этого концентрация начинала рост в этой точке, а граница окисления переносилась в соседнюю точку. Рассчитывались скорость границы окисления и время полного окисления канала.

Результаты вычислений дают значения to = 0,64 - D.                (17)

Скорость границы окисления при ^ <  r _o равна d ^ ~n D ^D e

-dt- ~ U, 32 • —, а при ^^0 она немного уменьша ется. В то же время аналогичное численное ре-

шение уравнения (4), соответствующее плоской геометрии, дает значения, совпадающие с аналитическим решением (8), (9).

Для сравнения с экспериментом рассмотрим результаты работы [11], где измерялось время переключения из «ON» в «OFF» состояние NiO переключателя с толщиной пленки 60 nm. Сопротивление канала составляло 54 Q , что при удельном сопротивлении р = 1 - 10^-6 Q- m дает исходный радиус канала r o = 20 nm. По оценке авторов статьи, температура канала равнялась ~ 900 K, а время переключения 2 _o = (1 ^ 2) - 10 ³ s. Расчет времени полного окисления канала по формуле (17) с коэффициентом диффузии (1) ( D ~ 1,4 - 10^-9 cm²/s при T = 900 K) дает 2 _o = 1,5 - 10^-3 s, что близко к экспериментально измеренному значению [11].

Таким образом, проведенный анализ показывает, что теплоиндуцированное диффузионное окисление никеля может быть решающим фактором исчезновения металлической проводимости канала и перехода из состояния «ON» в «OFF». Обратный переход (SET) является уже результатом «самозалечивания» канала переключения по схеме мягкого пробоя («soft break-down») [15] в условиях резкого увеличения напряженности поля и сопротивления структуры. По своей сути механизм этого перехода аналогичен электрической формовке (но происходит при меньших напряжениях) и включает другие, отличные от диффузии эффекты (полевая и ударная ионизация, прыжковая проводимость и т. п.), что требует дальнейших исследований.

В заключение отметим, что диффузионный механизм окисления проводящего канала может быть достаточно универсальным и определять переход RESET в других переключательных структурах, особенно в оксидах на основе переходных металлов (V, Ti, Nb, Ta и др.).

* Работа выполнена при поддержке Программы стратегического развития Петрозаводского государственного университета на 2012–2016 годы.

DIFFUSION MECHANISM OF NICKEL OXIDATION IN CONDUCTING CHANNEL OF Pt/NiO/Pt

SWITCHING STRUCTURE