Дифракция цилиндрических Н или Е поляризованных волн на конечной периодической структуре

Задача расчета поля рассеянного периодической цилиндрической структурой является классической задачей теории дифракции. Среди методов, предложенных для численного решения такой задачи, отметим, прежде всего, метод Релея [1], Тверского [2], метод токовых (сингулярных) интегральных уравнений [3-5] (включая метод полуобращения [4]), метод диаграммных уравнений [6] и вариационный метод Фельда [7]. Следует отметить, что все указанные методы с успехом использовались для расчета рассеянных полей бесконечными периодическими структурами или конечными структурами с относительно небольшим количеством элементов (N ~ 10 ^ 20). Число публикаций и обзоров, посвященных этой теме, к настоящему моменту огромно. Однако если число элементов периодической решетки конечно, но велико (например, N > 100), то применение указанных выше методов наталкивается на различные вычислительные трудно сти. С точки зрения практического использования таких структур укажем на то, что в последнее время стали широко использоваться периодические структуры с об- щим числом элементов порядка нескольких сотен или десятков тысяч. Поэтому разработка методов, которые позволяют получить решения задач рассеяния волн периодическими структурами с большим, но конечным числом элементов, в настоящее время является актуальной и важной как с теоретической, так и практической точек зрения.

В настоящей работе модифицированный метод дискретных источников (ММДИ) [8, 9] использован для численного решения задачи дифракции Е и Н поляризованных цилиндрических волн на 2D (двухмерных) периодических решетках (цилиндрических структурах) с произвольной формой поперечного сечения каждого элемента и конечным числом элементов.

ММДИ и задача рассеяния волн системой М цилиндров

Рассмотрим задачу дифракции цилиндрической волны:

и 0( r, ф) = н 02)( k|r - RoD (1) на конечной решетке, образованной идеально проводящими цилиндрическими поверхностями Si (i = 1, .„, M, где M - общее число цилиндров в решетке, Si - поверхность i-го цилиндра), расположенных в пространстве вдоль оси x декартовой системы координат {x, у}. В (1), (2) к - волновое число свободного пространства; {r, ф} - цилиндрические координаты точки наблюдения; R0 = {R0, ф0}- цилиндрические коор- динаты источника цилиндрической волны;

I r - 2801 = 7r2 + R0 - 2rRc-^- Po) -расстоя ние между точкой наблюдения {r, φ} и источником цилиндрической волны; H0(2) (•) – функция Ханкеля второго рода и нулевого индекса.

Будем считать, что форма поперечного сечения ρ_i { φ } каждого цилиндра описывается аналитической функцией:

ρ _i ( ϕ ) = ρ ( ϕ ) (2) в локальной системе полярных координат { r , φ }, связанной с каждым цилиндром решетки. Полное рассеянное поле U_r ( r , φ ) такой решетки представим в виде суперпозиции полей, рассеянных каждым цилиндром:

M

U r ( r , ϕ ) = ∑ U rj ( r , ϕ ) , (3) j = 1

где U – поле, рассеянное каждым j -м цилиндром: rj _N

U_r j (r, ф ) = £ A . H 0²⁾ ( k | r - j l); (4) l = 1

^г - координаты вспомогательных дискретных источников, расположенных на вспомогательных контурах (поверхностях) Σ _j в l -ых точках ( l = = 1, …, N ; N – общее число точек на каждом вспомогательном контуре Σ _j ) и уравнения контура поперечного сечения которого ρ _Σ ( θ ) = ρ _Σ ( θ ); H 02) ( k | r - r j. |) - поле вспомогательного источника расположенного в точке r j ;

A_lj – амплитуды поля вспомогательных источников, подлежащих определению.

Каждый вспомогательный контур ρ _Σ ( θ ) мы будем строить в соответствии с методом ММДИ [8, 9] как результат аналитической трансформации исходного контура ρ ( φ ):

^z i = P ^(Z> ) exp{i< p }; q ) = Ф + i9v

ρ _Σ = | ζ ₁|; θ = arg ζ ₁, (5) где параметр ϕ ₁ ′′ определяет деформацию исходного контура ρ ( φ ) [отличие каждого вспомогательного контура ρ _Σ ( θ ) от исходного контура ρ ( φ )] и степень его близости к сингулярностям рассеянного поля внутри рассеивателя [10]. В результате такой аналитической трансформации мы будем иметь систему вспомогательных контуров ρ Σ _j ( θ ), на которых и будут располагаться вспомогательные источники.

В случае Е поляризованной падающей волны (1) полное поле должно удовлетворить граничным условиям на поверхности каждого рассеивателя:

( U ⁰ + U r ) S_j = 0, j = 1,..., M , (6) а для Н поляризованной падающей волны (1) – граничным условиям:

U0 U r 0, j1,...,M. nnS

Удовлетворяя (7) иjли (8) в N точках на поверхности каждого цилиндра мы получим алгебраиче- скую систему M × N уравнений с M × N неизвестными Akj. Решение такой системы уравнений нетрудно получить, например, методом Гаусса. Подставляя найденные таким образом коэффициенты Akj в (3), (4), мы получим формулу для расчета ближнего поля решетки:

MN

U_r (r , Ф ) = £ £ A_tiH 0²⁾ ( k | r - r |).        (8)

j = 1 l = 1

Устремляя в (8) точку наблюдения к бесконечности ( r →∞ ) , мы получим выражение для диаграммы рассеяния g ( φ ) решетки:

MN

g ( ϕ ) = ∑∑ A_lj exp[ ikr_lj cos( ϕ - θ _lj )],       (9)

j = 1 l = 1

где r_lj , θ_lj – координаты вспомогательных дискретных источников.

Обсуждение результатов расчетов

Рассмотрим сначала задачу дифракции Н поляризованной цилиндрической волны на решетке, составленной из идеально проводящих круглых цилиндров, которые расположены вдоль оси x декартовой системы координат { x , y }. При расчетах мы придерживались следующих обозначений, характеризующих геометрию решетки: общее число элементов в такой решетке – N ; период решетки – T ; радиус цилиндра – а ; координаты источника цилиндрической волны в декартовой системе координат – Rx , Ry .

На рис. 1 представлены результаты расчетов нормированной диаграммы рассеяния для четырех значений общего числа элементов решетки N = 11, N = 33, N = 101 и N = 181. При этом полагалось, что «электрический» радиус цилиндра был равен ka = 0,1 kT ; «электрический» период решетки был равен kT = 1,5π; «электрические» координаты источника цилиндрической волны – kRx = 0,5 × ( N – 1) kT , kRy = –[ ka + 2 kT ]. Отметим, что случай бесконечной решетки с аналогичными параметрами рассматривался в работе [6]. Сравнивая результаты, приведенные в [6], с результатами, представленными на рис. 1, мы придем к следующим выводам. Присутствие второй распространяющейся гармоники в конечной решетке (что характеризуется наличием четырех узких пиков в диаграмме рассеяния) отчетливо формируется при числе элементов N > 50. В диаграмме рассеяния конечной решетки всегда присутствуют волны, отраженные от ее концов, что приводит к появлению дополнительных осцилляций диаграммы рассеяния. Для решетки с числом элемен-

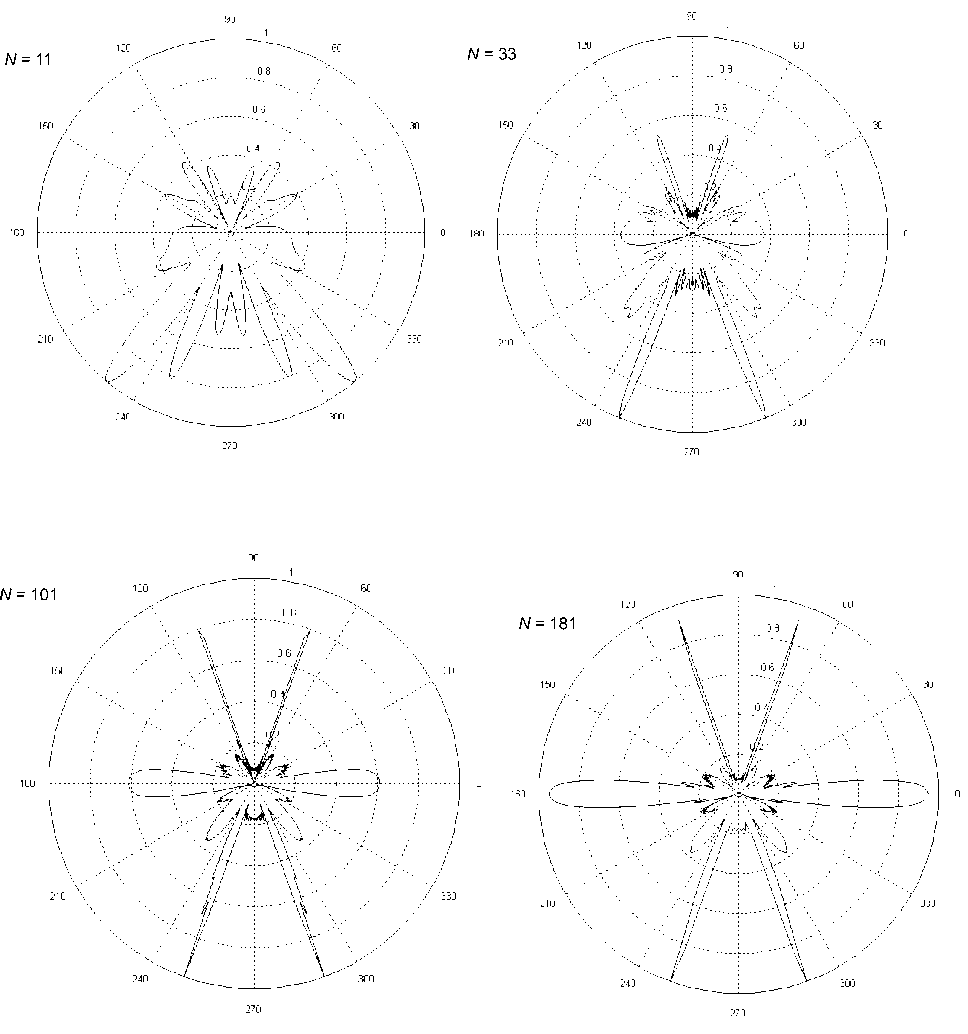
Рис. 1. Нормированные диаграммы рассеяния в случае источника Н поляризованной цилиндрической волны

тов N >  50 характерно наличие излучения в направлениях ф = 0 и ф = п , то есть вдоль решетки.

Рис. 2 иллюстрирует нормированную диаграмму рассеяния в случае источника Е поляризованной цилиндрической волны с координатами kRx = 0,5 х ( N — 1) kT , kRy = -[ ka + 2 kT] на решетке из N = 181 круглых цилиндров. При этом период решетки был равен kT = 1,5 п (то есть оставался таким же, как и в случае на рис. 1), а радиус цилиндра - ka = 0,5 п .

Основные отличия диаграммы рассеяния, представленной на рис. 2, от рассмотренного выше связаны с уменьшение уровня осевого излучения и образование многих лепестков. При этом направления максимумов излучения второй гармоники остались прежними.

На рис. 3 представлены результаты расчетов нормированной диаграммы рассеяния для двух значений общего числа элементов решетки N = 101 и N = 181 и других параметрах решетки.

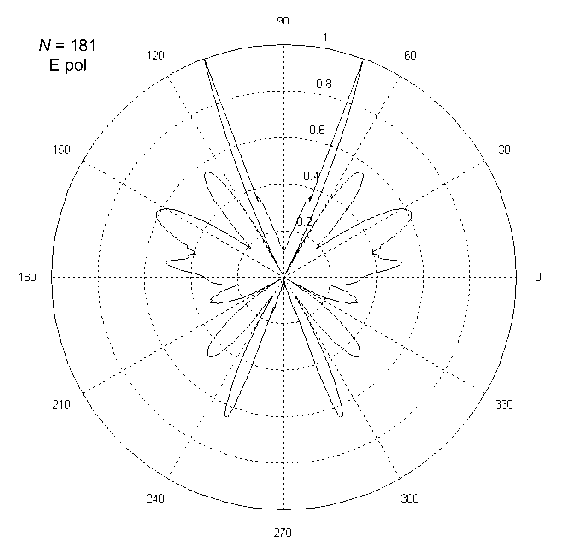
Рис. 2. Нормированные диаграммы рассеяния в случае источника Е поляризованной цилиндрической волны

При расчетах полагалось, что «электрический» радиус цилиндра был равен ka = 0,3 kT ; «электрический» период решетки был равен kT = 0,45 π ; «электрические» координаты источника цилиндрической волны – kRx = 0,5 × ( N – 1) kT , kRy = = –[ ka + 2 kT ].

Из сравнения данных рис. 3 с данными рис. 1 следует, что радиус цилиндра и период решетки могут существенно изменить структуру диаграммы рассеяния.

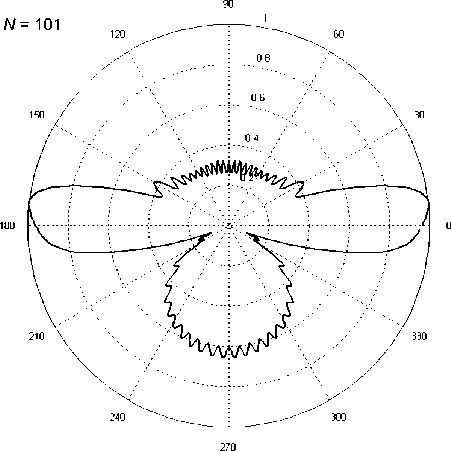
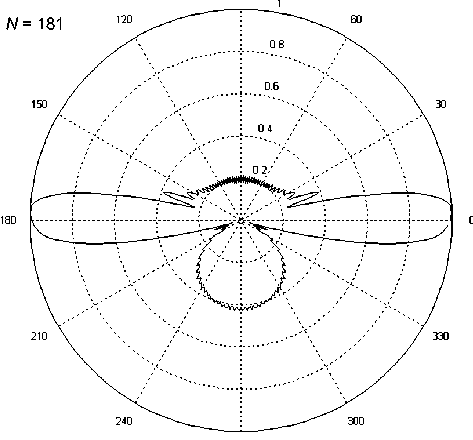
Рис. 3. Нормированные диаграммы рассеяния в случае источника Н поляризованной цилиндрической волны

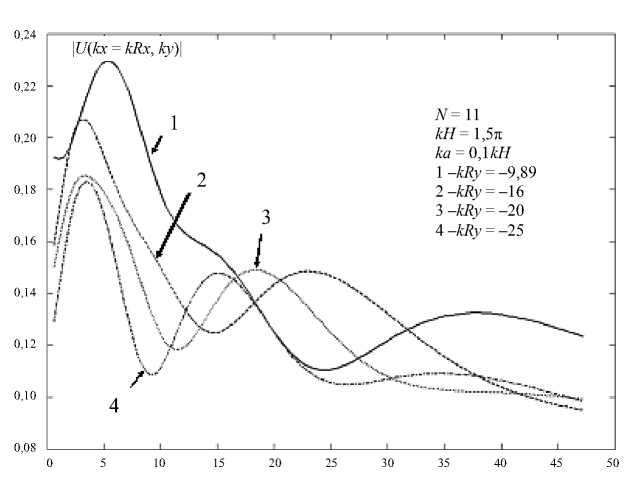
На рис. 4–6 изображено пространственное распределение амплитуды поля вблизи решетки с параметрами: kT = 1,5π, ka = 0,1kT, N = 11 для случая цилиндрической Н поляризованной волны. При этом источник цилиндрической Н поляризованной волны имел фиксированную пространственную координату kRx = 0,5 × (N – 1) kT, а другая пространственная координата kRy при- нимала значения, указанные на соответствующих рисунках. Точка наблюдения имела фиксированное значение пространственной координаты kRx = 0,5 × (N – 1) kT, то есть располагалась в середине структуры. Поэтому рис. 4–6 характеризуют пространственное распределение амплитуды поля вдоль оси y для центральной точки решетки.

,

0        5        10        15        20       25        30       35       40       45        50

0,24

0,22

0,20

0,18

0,16

0,14

0,12

0,10

| U ( kx = kRx , ky )|

N = 11 kH = 1,5π ka = 0,1 kH 1 – kRy = –9,89 2 – kRy = –16 3 – kRy = –20 4 – kRy = –25

Рис. 4. Пространственное распределение поля при различном положении источника цилиндрической волны

0,50

0,45

0,40

0,35

0,30

0,25

0,20

0,15

0,10

0,05

|U(kx = kR > 0, ky)| ky

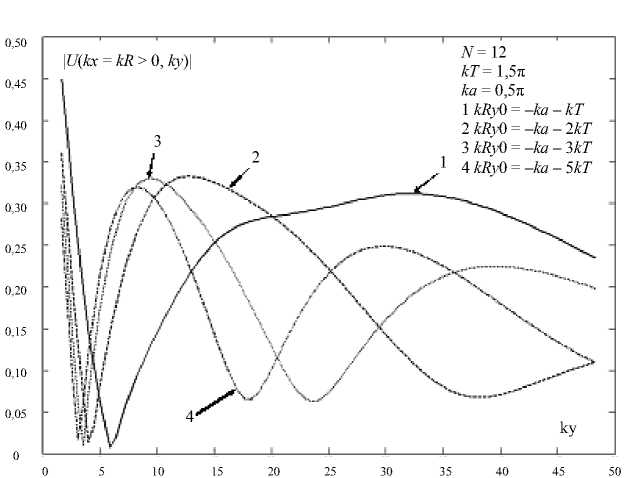
N = 12

kT = 1,5π ka = 0,5π

1 kRy 0 = – ka – kT

2 kRy 0 = – ka – 2 kT

3 kRy 0 = – ka – 3 kT

¹ 4 kRy 0 = – ka – 5 kT

0         5        10        15        20       25        30        35        40        45        50

Рис. 5. Пространственное распределение поля при различном положении источника цилиндрической волны

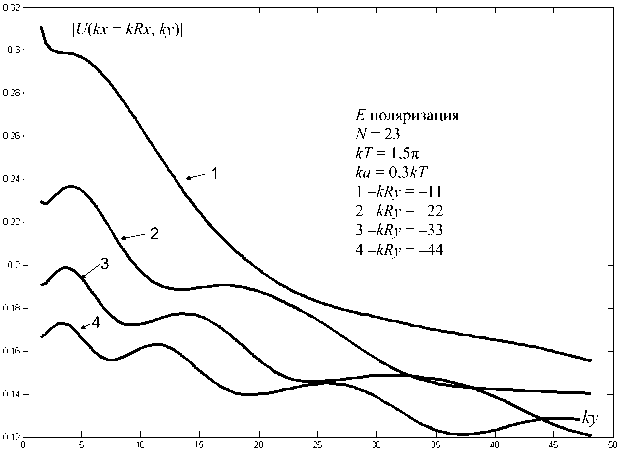
Рис. 6. Пространственное распределение поля при различном положении источника цилиндрической волны

Из приведенных выше рисунков видно, что пространственное распределение амплитуды поля за решеткой изменяется немонотонно (осциллирует) и содержит несколько максимумов. Отметим, что наличие таких максимумов не может быть интерпретировано в терминах геометрической оптики, поскольку их происхождение связано с процессом дифракции волны на решетке.

Рассмотрим теперь задачу дифракции Е по- ляризованной цилиндрической волны на решетке, составленной из идеально проводящих цилиндров, которые расположены вдоль оси x декартовой системы координат {x, y}. Поперечное сечение каждого цилиндра описывается уравнением:

P i ( ф ) = р ( ф ) = a + b cos( q ф ), q = 4.       (10)

Геометрия такой задачи представлена на рис. 7.

Q {Rx, Ry}

Рис. 7. Геометрия задачи

На рис. 8 представлены результаты расчетов нормированной диаграммы рассеяния в случае источника Е поляризованной цилиндрической волны, который имел координаты kRx = 91,9816; kRy = –9,89602. Параметры, характеризующие геометрию поперечного сечения одиночного цилиндра (10) решетки, полагались равными: ka = 0,075 kT ; kb = 0,025 kT ; период решетки kT = 1,5π; общее число N элементов решетки указано на рис. 8.

Из рис. 8 видно, что вторая гармоника начинает формироваться при больших значениях числа элементов решетки ( N > 80). Тем самым показано, что геометрия элемента периодической решетки сказывается на формировании пространственных гармоник рассеянного поля.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (грант № 10-02-01103).

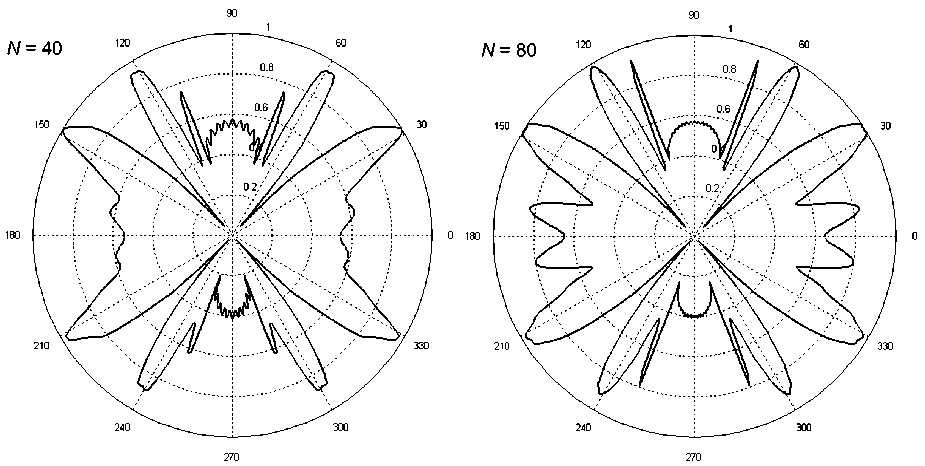
Рис. 8. Нормированные диаграммы рассеяния в случае источника Е поляризованной цилиндрической волны