Дифракция Фраунгофера на многоуровневой (квантованной) спиральной фазовой пластинке

Спиральной фазовой пластинкой (СФП) называют оптический элемент, у которого фаза функции комплексного пропускания линейно зависит от угловой полярной координаты. Вихревым пучкам, формируемым таким оптическим элементом, в современных научных исследованиях уделяется большое внимание. Основные причины этого интереса заключаются в повышении точности изготовления оптических элементов, формирующих эти пучки, и в возможности решения с их помощью прикладных задач. Важнейшей из таких задач является манипуляция микрочастицами [1]. Кроме того, область применения оптических вихрей постоянно расширяется. В [2] предлагается их использовать для фотолитографии с разрешением X/ 10, X - длина волны света. На основе СФП, помещенной в плоскость пространственного спектра 4 f – оптической системы ( f – фокусное расстояние сферической линзы) в [3] предложен способ получения спиральных интерферограмм. С помощью спиральной интерферограммы легко различать выпуклые и вогнутые участки волнового фронта. СФП используется также в звездном коронографе [4], в котором свет от яркой звезды преобразуется в кольцо и диафрагмируется, а слабый свет от планет этой звезды проходит через диафрагму и регистрируется. В [5] СФП применяется для выполнения радиального преобразования Гильберта, с помощью которого можно подчеркивать контуры на оптических изображениях.

Существует множество способов изготовления СФП, например, путем многоступенчатого травления кремния [6] или с помощью абляции эксимерным лазером полиамидной подложки [7]. Микрорельеф формируемой СФП получается ступенчатым или квантованным.

Многоуровневые СФП исследовались в [8, 9]. В [8] теоретически посчитано, с какой эффективностью преобразует ступенчатая СФП Гауссов пучок в моду Лагерра-Гаусса (0, 1), а также проведен эксперимент с 16-уровневой СФП, изготовленной по технологии фотолитографии.

В [9] теоретически найдены минимальные числа уровней фазы СФП (для номеров n < 8 ), при кото- рых конечно-уровневые СФП слабо отличаются от непрерывной СФП. С помощью конечно-уровневой СФП, реализованной на основе жидкокристаллической ячейки, в [9] сформированы вихревые лазерные пучки с номерами сингулярности до 6.

В [10, 11] рассматривается ахроматическая СФП, которая формирует почти одинаковые вихревые поля, если длина волны освещающего излучения меняется в достаточно широком диапазоне (140 нм). В этих работах [8-11] СФП анализируется с помощью разложения в ряд по угловым гармоникам:

= 1L C m exp ( im ф ) , ⁽¹⁾ m =-»

, ( P ф ) 2 n n exp i mod

I 2 n) P

где mod ( ... ) - целое число, P - общее число уровней фазы СФП, ф - азимутальный угол полярной системы координат, n – номер СФП, C_m – комплексные коэффициенты, exp ( im ф ) - угловые гармоники, описывающие пропускание непрерывной СФП с номером m .

В данной работе рассматривается конечно-уровневая СФП, ограниченная полиномиальной апертурой. Причем число уровней квантования фазы СФП равно числу сторон правильного многоугольника, ограничивающего апертуру СФП. В этом случае удалось получить аналитические выражения в виде конечной суммы плоских волн для комплексной амплитуды, описывающей дифракцию Фраунгофера плоской волны на конечно-уровневой СФП, ограниченной правильным многоугольником.

Заметим, что ранее уже рассматривалась возможность формирования вихревых полей с помощью неспиральных фазовых пластинок [12]. В нашем случае, в отличие от [12], при увеличении числа уровней квантования фазы (или числа сторон многоугольника), картина дифракции в дальней зоне стремится к картине дифракции, сформированной непрерывной СФП с круглой апертурой.

• 1.    Уравнение полиномиальной апертуры

Пусть Q - многоугольник, заданный координатами своих вершин A_p ( x_p , y_p ) , p = 0, P - 1, где P -число вершин (рис. 1).

Пусть уравнение стороны многоугольника, соединяющей p -ю и ( p + 1 ) -ю вершины, имеет вид:

• У = a p x ⁺ b p .                                    ⁽²⁾

Пусть f ( x , y ) - функция двух переменных, определенная в R ² следующим образом:

,/ х J1(x,У)eQ, ^^’ У^ [0, (x, У )eQ

Известно, что преобразование Фурье от такой функции f ( x , y ) вычисляется с помощью уравнения полиномиальной апертуры [13]:

Ц exp [±i (x ^ + y n)] dx dу = у

Q                                      p = 1

a p - a p - 1

(^ + Пap—1 )(^ + Пap)

exp

[± iM xp

+ ПУp )] =

(yp+1 -yp)(xp -xp-1)-(yp -yp-1)(xp+1 -xp)            г угк/ \   / м           \   (        Mexp [± i (^x p+ny ■

p=1 [^ ( xp+1- xp )+n (yp+1- yp ШЦ xp- xp-1)+n (yp- yp-1)]

где под индексами p подразумеваются значения mod ( p , P ), т. е. ( x_P , y_P ) = ( x ₀, y ₀ ) , ( x _{- 1}, y _{- 1} ) = ( x_{P - 1}, y_{P - 1} ) и т. д.

Тогда комплексная амплитуда, описывающая дифракцию Фраунгофера на полиномиальной апертуре

(рис. 1) плоской волны длиной X при фокусном расстоянии сферической линзы, равном f , имеет вид:

E (Е п) = - JC у       (yp+1- yp)(xp- xp-1)-(yp- yp-1)(xp+1- xp)

,        ^{2 п} k p = ¹ [^ ⁽ x p + 1 ^- x p ) + n ⁽ y p + 1 ^- y p ) ][Л x p ^- x p - 1 ^{) +} n ⁽ y p ^- y p - 1 ) ]

exp ± ik ( ^ x p

+ Пyp)

где k = 2 njX - волновое число.

2. Дифракция Фраунгофера плоской волны на ДОЭ с формой правильного многоугольника и кусочно-постоянным микрорельефом

Q = ^ Q _p , где П _p - треугольники OA_p A_{p + 1}, а каж- p = 0

дая вершина A_p имеет координаты (рис. 2)

x p = R cos ^ p - P

( n' b p = R sin |ф p - P

2n

» ,=Pp.

Пусть внутри каждого треугольника Q _p глубина микрорельефа имеет постоянное значение, тогда внутри Q _p и функция комплексного пропускания ДОЭ будет постоянна:

^T ( ^x , y ) = exp ( i Y p ) . ⁽⁷⁾

Пользуясь уравнением для полиномиальной апертуры, можно получить выражение для комплексной амплитуды, описывающей дифракцию Фраунгофера плоской волны длиной X на таком ДОЭ (рис. 2):

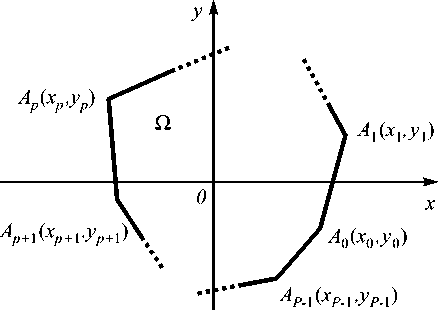
Рис. 1. ДОЭ с многоугольной апертурой

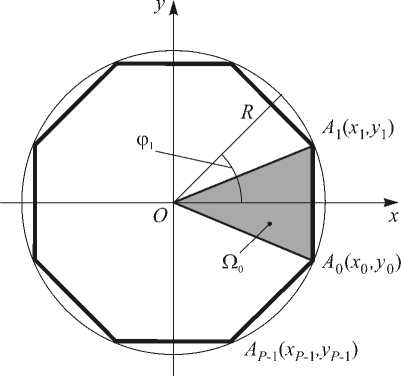
Рис. 2. ДОЭ с апертурой в виде правильного многоугольника

P 1

E (§, n) = -if-R ² sin I — |E^- ( ) 2 n k I P J p Z0 ( ^ x

exp (iТ p)

■ p + 1 +П У p + 1 )( ^ x p +П У p )

^^^^^^B

if        f 2 n) P -

—— R ² sin I    I E

2 n k       ( P J p :0 ^^ (,

^exP ( i ^Т p ) ^exP ^- i j ( ^ x p ⁺ n У p )

x p + 1 - x p ) + n ( y p + 1

^^^^^^B

Ур )](^p +nУр )

if        f 2 л) P

+ R ² sin I I E

2n k      ( P J pz0

^exP ( i ^Т p ) ^exP ^- i у ( ^ x_P + i ⁺ П У p + i )

( ^ x p + 1 +П У p + 1 ) [^ ( ^xp + 1 - ^xp ) + n ( y p + 1

^^^^^^B

При переходе к полярным координатам вместо (8) получается следующее выражение:

e ( p , 9 ) = sin fan) ^Pt —_f—^{6 (}    ) ²ⁿ k p 2    ^ P ^IEcos Гф, + «

I ^p P

^exP ( i ^Т p )

^-9 I ^cos I ф p

-------X +

---9 ⁾

P I

if       n P —1

----- cos — E 2n k p     P p ~0

exP ( i Т _p )     exP ( i Т

_ ^sin ( ф p ^-9 ) ^sin ( ф p -1

. kR p f n

) 1 exP [" if cos (ф p - P -

^^^^^^B

⁹ ) ]

f n cos ф - -9 I p p

.

В случае СФП, т. е. Т _р = n ф _р , из (9) получим:

E P ( Р , 9 ) =

P-1 xE p =0

if . f 2 n) sin I I x

2nkp ( P J exp (in Ф p)

n ) f

cos ф„ +--- \ ^p P

if      n

+ cos x

2 n k p     P

P -1 x E p =0

^exP ( in Ф р )    ^exp ( in ф р -I )

_ sin ( ф p ^-9 ) sin ( ф p -i

^^^^^^в

X

X

. kR p f exP — if ^C°s (Ф p

n ^^^^^^B  ^^^^^^^^^™  ^^^^^^B

P

f n cos фп---9

\ p P

.

где у = R p = kR p/ f , J_n ( x ) - функция Бесселя n -го порядка,

j J0 (t) d =

0                                                  (12)

= У {mJ1 ( y ) H0 ( y ) + J0 ( y )[2-nH1 ( y )]},

H 0 1 ( У ) — функции Струве нулевого и первого порядков.

При расчете использовались следующие значения параметров: длина волны – 633 нм, фокусное расстояние сферической линзы – 150 мм, радиус апертуры – 2 мм, порядок СФП 6.

На рис. 4 показаны картины дифракции Фраунгофера плоской волны на квантованной ограниченной СФП, полученные по формуле (10).

3. Численное моделирование

На рис. 3 показана картина дифракции Фраунгофера плоской волны на непрерывной СФП, ограниченной круглой диафрагмой, полученная по формуле конечных сумм функций Бесселя [14]:

E. ( Р , 9 ) =

( - i ) n ^{+ 1} k exp ( in 9 )

f p ² ( n - 2)/2

X

(а)

(б)

Рис. 3. Картина дифракции Фраунгофера плоской волны на непрерывной ограниченной СФП: амплитуда (а) и фаза (б)

n ^{1 -} J 0 ( У )^{- 2} E J 2 m ( У ) ^- y^J n - 1 ( У ) ’ n = ² m ’

n

m = 1

У                    ( n - 1)/2                "

j J 0 ( t ) dt ^{- 2} E ^J 2 m - 1 ( У ) ^- y^J n - 1 ( У ) 0                  m = 1

, n = 2 m + 1,

(а)

(г)

(б)

(д)

(в)

(ж)

(з)

(к)

(л)

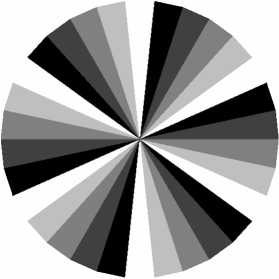
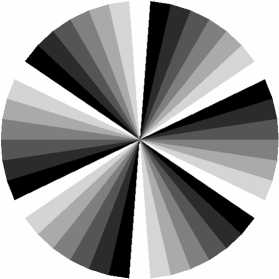
Рис. 4. Картины дифракции Фраунгофера плоской волны на квантованной ограниченной СФП: фаза ДОЭ (а, г, ж, к), амплитуда (б, д, з, л) и фаза (в, е, и, м) в зоне дифракции Фраунгофера.

Число секторов: 18 (а-в), 30 (г-е), 42 (ж-и), 54 (к-м)

В таблице 1 показана зависимость среднеквадратичного отклонения картины дифракции Фраунгофера плоской волны на ограниченной квантованной спиральной фазовой пластинке от картины дифракции на ограниченной непрерывной СФП при меняющемся количестве секторов.

Таблица 1

Число секторов	СКО
18	19,1411
30	1,9003
42	0,1320
54	0,0479

В таблице 2 для нескольких номеров СФП показано минимальное количество секторов многоуровневой СФП, при котором среднеквадратичное отклонение картины дифракции Фраунгофера от картины дифракции для непрерывной СФП не превышает 2%.

Таблица 2

Номер СФП	Минимальное число секторов
2	19
4	25
6	29
8	35
10	39

Заключение

В работе были получены аналитические выражения, описывающие параксиальную скалярную дифракцию Фраунгофера плоской волны на многоуровневой (квантованной) СФП, ограниченной апертурой в виде правильного многоугольника. Для нескольких номеров СФП численно получено минимальное количество секторов многоуровневой СФП, при котором среднеквадратичное отклонение картины дифракции Фраунгофера от картины дифракции для непрерывной СФП не превышает 2%.

Работа выполнена при поддержке российско-американской программы «Фундаментальные ис- следования и высшее образование» (грант CRDF RUX0-014-Sa-06), а также грантов РФФИ 05-0850298 и 07-07-97600.