Дифракция Френеля на отверстиях с произвольной формой контура

В теории Френеля-Кирхгофа для нахождения дифракционного поля за отверстием в непрозрачном экране в общем случае необходимо вычислить поверхностный интеграл от быстроосциллирующей функции, что представляет собой непростую задачу даже для современных ЭВМ. Имеется несколько простых типов отверстий, например, прямоугольное и круговое отверстия, для которых интеграл удается выразить через известные специальные функции, подходящие для численных расчетов. В работе [1] был предложен простой и наглядный способ преобразования поверхностного дифракционного интеграла в линейный интеграл по контуру отверстия при нахождении точки наблюдения в зоне Френеля. Данный подход имеет ряд преимуществ. Так, вычисление одномерного интеграла заметно проще вычисления исходного поверхностного интеграла и, кроме того, при необходимости легче осуществить его оценку асимптотическими методами, например, методом стационарной фазы.

В данной работе рассматривается применение результатов, полученных в [1], для решения задач дифракции на отверстиях с произвольной формой края на примере эллиптического отверстия и параболического края.

В [1] для множителя прохождения W=U/U₀, где U_o и U - падающее и прошедшее поля соответственно, в случае параметрического задания контура отверстия уравнениями х = 7(f), у = 7?f) Д g [Zq И х -

( L J) было получено следующее выражение:

где е = 1, если точка наблюдения находится в освещенной области, и е = 0 в случае нахождения ее в тени, Ь² = МДУД+ад - радиус первой зоны Френеля в плоскости препятствия, X - длина волны, dy d₂ - расстояния источника до экрана с отверстием и от экрана до точки наблюдения соответственно, х_с = Xpd^/Д + d₂), у_с = ypd^/Д + d^ , (х_Р, у_Р) - координаты точки наблюдения.

В отличие от кругового отверстия представление поля эллиптического отверстия в виде одномерного интеграла при традиционном подходе не существует. Поле эллиптического отверстия, край которого описывается параметрическими уравнениями v = .lcos/. у = Вsinf (/ е |().2^|). имеет вид

2тг, тгг 1 С       cosi+угЛsini-АВ•

Ж = £4---— ------^с, ----------77г ехр —- (Л cos t - х_г Г + (В sin t - у с

2я i (Acost — хД+ (Вsint — уД

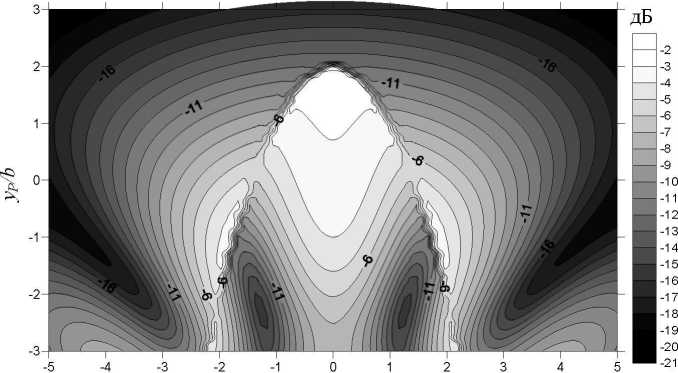
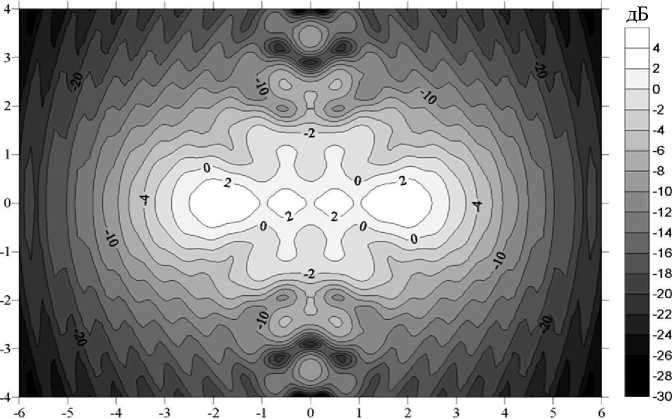
На рис. 1 приведено пространственное распределение |йЛ|, рассчитанное по формуле (2), в плоскости, параллельной плоскости отверстия.

Рассмотрим препятствие, имеющее параболическую форму. В данном случае также не существует решения в виде однократного интеграла. Пусть край такого препятствия задан уравнением вида у = Н-Ах². Тогда множитель прохождения, согласно (1), запишется в виде

1 Ж Н -   - Ах² + 2Ах(х-Х_г) ,                   Г5Л

И =е+ - ехрВ- (д-д^У + (Н - v_r-Ах")" Г

2x1                            J (д х_с)²+(Н-у_с-Ах²)²

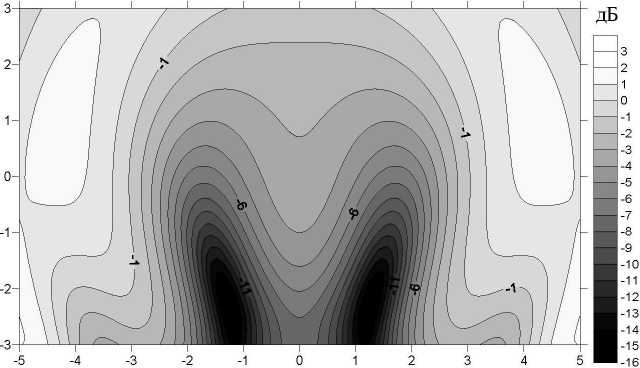
На следующих рисунках представлены результаты численных расчетов, выполненные по формуле (3).

Хр/Ь

Хр/Ъ

Рис. 1. Распределение уровня поля за эллиптическим отверстием. А/В = 2.

ВЖ Архинчеев, Н.В. Юможапова. Влияние электрического поля на диффузию и распределение частиц в пористых нано-структурированных материалах

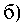
Хр/Ъ

Рис. 2. Распределение уровня поля за параболическим отверстием: а) граничная волна; б) полное поле. Н = 4л ]b , Л = 2б/ Vr

Таким образом, в работе приведены выражения для граничной волны в области дифракции Френеля для эллиптического отверстия и параболического края в виде однократных интегралов.