Дифракция гауссова пучка на обобщённой линзе

Вторая половина прошлого века ознаменовалась бурным интересом к бездифракционным пучкам [1, 2], которые наиболее эффективно производятся с помощью рефракционного [3] или дифракционного [4] аксикона. Данный факт определил важное место аксикона в современной оптике.

Известно, что сочетание аксикона с другим классическим элементом – параболической линзой – позволяет управлять как продольным, так и поперечным распределением лазерных пучков [5–7]. При этом формируется коническая фокальная область с переменным размером центрального светового пятна [7, 8].

В работе [8] был предложен новый оптический элемент, названный фраксиконом, который является обобщением как аксикона, так и линзы. Фраксикон является фазовым оптическим элементом с дробной степенью зависимости от радиальной координаты.

В работах [8,9] подробно исследовались свойства фраксикона, освещаемого плоской волной и было показано, что за счёт вариации параметров можно получить не только аналог линзакона [5], но и логарифмического аксикона [10] без сингулярности в центральной части оптического элемента.

В работе [9] фраксикон исследовался с помощью модифицированного метода стационарной фазы и рассматривался как обобщённая параболическая линза. Были получены аналитические и численные оценки продольного и поперечного комплексного распределения при дифракции на фраксиконе ограниченного плоского пучка. Однако в связи с резким ограничением плоского пучка на краях апертуры распределение формируемой интенсивности испытывает существенные осцилляции. Чтобы осевое распределение интенсивности было гладким, необходимо использовать Гауссов освещающий пучок.

В данной работе аналитически и численно исследуется дифракция Гауссова пучка на фраксиконе и обсуждаются основные отличия от дифракции на этом элементе ограниченной плоской волны.

1. Анализ осевого распределения

Рассмотрим дифракционный фраксикон [8], фаза которого имеет произвольную степень зависимости от радиальной координаты:

т ( r ) = exp [- i ( k « 0 r ) ^Y J , r <  R , (1) где k = 2 n / % , % - длина волны, у - положительное действительное число, а ₀ — безразмерный коэффициент, связанный с числовой апертурой оптического элемента и определяющий максимальный угол наклона лучей к оптической оси.

Комплексная функция пропускания фраксикона (1) позволяет рассматривать его также как обобщённую параболическую линзу [9].

Дифракция произвольного осесимметричного пучка с медленно меняющейся амплитудой A ( r ) и постоянной фазой ф ₀ на оптическом элементе (1) в параксиальном приближении вычисляется по формуле:

k            ik Р 2

U ( Р , z ) = —exp ^{lkz 1} ' * ¹ Ф о iz             2 z

R

xj A (r) т( r) exp

ikr ² 2 z

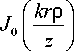
r d r .

На оптической оси формула (2) примет вид:

k

U ( p = 0, z ) = — exp ( ikz + 1 ф ₀ ) x iz

R xj A(r)exp -i (ka0r )Y

0 L

ikr ²

+--

2 z

r d r .

Интеграл вида (3) удобно вычислять методом стационарной фазы [11]. Основная стационарная точка r 0 подынтегральной фазы:

v( r ) = -( kao r )Y+ kp

2 z

равна r0

Y z a 0 ) ^2-Y

I1-7" I

Вторая стационарная точка r 1 =0 имеет место не при всех значениях у , и её вклад обычно мал [9].

Значения фазы (4) и её второй производной в основной стационарной точке равны:

V(ro ) =

Y k ■ )5=2 ( 2

2 z « Y

VY Г , ) = 2( Y- 2)

V Y k1-Y '

2I^,

Y

Выражения для U pl ( z ) при различных значениях степени фраксикона y детально обсуждались в работе [9].

В частном случае, когда падающий пучок является Гауссовым:

2 z « 0

.

Используя метод стационарной фазы, мы аппроксимируем функцию (4) следующим образом:

V(r ) = V( r0 h^y0) (r - r0 )2.

Учитывая (6), можно переписать выражение (7), выделив в явном виде зависимость от радиуса:

kr ^{2 k} ( ^{2 -} y ) r

V ( ^r ) = ( ^{2 -}y)-— ^v ’ 2 z

z

r ⁺ V 1 ( r o ) .

Выражение (8) можно рассматривать как локальную аппроксимацию фраксикона тандемом из линейного аксикона и параболической линзы:

Y kr

-( k «0 r ) + T2z- = kr2          kr2

- ka0(z)r + —+ (1 -Y) —+V1 (r)), 2z         2z

где ^a 0^{( z} ) = ^{(2 -}Y ) ^r 0/ z .

Т.е. при использовании метода стационарной фазы интенсивность на оптической оси от фраксикона рассматривается как вклад от линейного аксикона с меняющимся в зависимости от расстояния z параметром a ₀( z ) (рис. 1), а также с дополнительной степенью расфокусировки (1- y ). Очевидно, при Y>1 дополнительный сферический волновой фронт из рассеивающего превращается в собирающий.

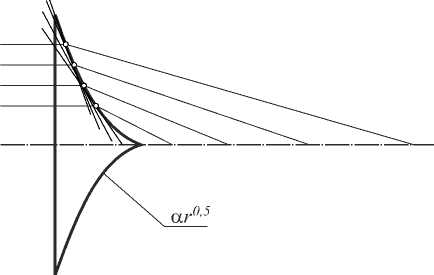
Рис. 1. Иллюстрация к методу стационарной фазы как дифракции на локальном аксиконе

Разумеется, локальная аппроксимация линейными аксиконами применима к любой фазовой функции, к которой применим метод стационарной фазы. В частности, аналогичный подход был применён к анализу логарифмического аксикона [12].

В условиях медленной зависимости амплитуды падающего пучка A ( r ) интеграл (3) можно вычислить как произведение амплитуды пучка в стационарной точке A ( r ₀) на комплексную амплитуду, полученную при освещении фраксикона плоской волной:

U (z ) = A (ro) Upl (z).

A ( r ) = exp |^- r^ V 2 0

,

можно получить более точное решение. В этом случае, выделяя полный квадрат, получим следующее выражение:

k ₂

Ugl (z) = — exp (ikz + iф0) exp (iцr02 ) x

x exp |^ - i ( k a ₀ )^Y v ( r ₀ ) J exp

R

xjexp [-ц (r - r )2 J r dr, где

-

2 2 Y g r 0 lx

Ix

Ц1 )

k 1           Цr g= (2-Y)—, Ц1 = л-г-iЦ , r1 = —.

2 z       2 o             i Ц 1

Интеграл в (12) можно вычислить с использованием различных модификаций метода стационарной фазы [9] с вариациями в сложности и соответствующей точности аналитических оценок.

Наиболее простое выражение получится при вынесении r = r ₀ за интеграл и расширении пределов до бесконечных. В этом случае оценка интеграла (3) имеет следующий вид:

U g^ ( z ) = z ^r 0 ^^ exp ( ^{ikz +} i ^ 0 ) exp ( i g ^r 0² ) ^x

x exp |^ - i ( k a ₀ ) ^Y V ( r ₀ ) J exp

-

2 2 Y ц r) l

Ц 1 ) ,

Интенсивность, соответствующая (13), имеет следующий вид:

T , x (k Y   2no2

выражению

xexpl -

I r I ;         2 4 xV z ) 71 + 4ц2о4 4ц2r02o2 )

1 + 4 ц ² о 4

.

Чтобы выделить в явном виде зависимость от расстояния z , перепишем выражение (14) в следующем виде :

Y

I gs ( z ) = z ^2-Y

2 no ² p

4 z ² + (2 -Y ) ² 0 4 k²

x

x exp

где

(     2                 )

z^{2 -Y} (2 -Y ) ² 0 2 p

-

V

z ² + (2 -Y ) ² 0 4 k ² ’ )

p = (ky«Y) 2-y .

В дальней зоне оценка (15) упрощается следующим образом:

2 у- 2

Igs (Z ^ У = Z 2 Y 2ЛО2p X

В принятом приближении максимальное значение на оптической оси будет на расстоянии:

x exp

(     2 y- 2

„ 2-y

^- z

V

1 (2 -у ) о p .

J

z ^gs max

1-2

1       ( 21 2

Yka0 (ka)Y 2 VYJ

Эта оценка только качественно описывает факт стремления интенсивности к нулю в дальней зоне, так как на самом деле из формулы (3) следует, что интенсивность должна быть пропорциональна z ^–2.

В ближней зоне оценка (15) сводится к выражению:

IgД z ^ 0 ) = z2-Y -2^ x ’        k |2-y|

( x exp -z Jk°) p

V J

Очевидно, характер зависимостей (16) и (17) главным образом определяется значением параметра у , т.е. типом фраксикона. В табл. 1 приведены оценки (17) для конкретных значений у из характерных диапазонов.

Таблица 1. Характер зависимости осевой интенсивности от расстояния z

	z ^ 0
Y^ 0	I ∼1 gs
0 <  y< 1, Y = 0,5	I ∼ z 13 gs
Y = 1	gs
1 2, Y = 1,5	I ∼ z 3 gs
Y >  2 + e	I gs - z "” exp ( -в z "” )
Y> 2, Y = 3	I gs ~ z 'exp ( -в z "2 )
Y ^ ^	I gs - (Y г )

В случае, когда ближняя зона не является теневой (0< у <2), увеличение у приводит к более резкому уменьшению интенсивности, но оно всё равно остаётся степенным.

Если ближняя зона является теневой ( у >2),

Для сравнения, в работе [9] была получена оценка для расстояния, на котором формируется максимальное значение интенсивности при освещении фракси-кона плоской волной, ограниченной радиусом R :

= R ”x Y«Y( kR

В табл. 2 приведены оценки (19) и (20) для конкретных значений y из характерных диапазонов.

Таблица 2. Положение максимума интенсивности на оптической оси

	Гауссов пучок	Ограниченный плоский пучок
Y = 0,5	z g- =a 5° ”x      2 a 0	pl          kR max \ a0
Y = 1	zgs = O max    V2 a 0	zp = R z max a 0
Y = 1,5	zgs = 0,62 ГУ z max a 0    k a 0	pi = 0,67 ПГ z max            4 J 7 a 0 \ k a 0
Y= 2	zgs =    1 max    2 k a 0	z pl = —1— max 2 k a 2
Y= 3	zgs = 0,27 ”ax    о k 2 a 3	pl 0,33 z max Rk V0

Как следует из сравнительного анализа (учитывая, что о <  R ), при y <2 освещение Гауссовым пучком приводит к формированию фокуса ближе к оптическому элементу, чем освещение плоским пучком. Тип освещающего пучка не влияет на положение фокуса при использовании классической параболической линзы ( y =2). При y >2 фокус оказывается ближе при освещении обобщённой линзы плоским ограниченным пучком.

Такое сравнение также легко получить из анализа отношения:

уменьшение интенсивности принимает экспоненциальный характер, увеличение у его ослабляет.

Таким образом, наиболее резкое уменьшение происходит при использовании классической параболической линзы ( у =2).

Определим расстояние, при котором достигается максимальное значение интенсивности (15). Для упрощения анализа пренебрежём слагаемым z ² в пока-

зателе экспоненты и под корнем:

Igs ( z) ”

^{2 п} p _z У

(2 -Y ) k

exp ■

2    1

p о2 k2

П =

pl max

z ^gs max

(6 о1 л 2 R J

Y- 2

Очевидно, что П =1 при Y =2 и п >1 при Y< 2. При y >2 отношение (21) будет сначала меньше единицы, но с ростом Y снова превысит единицу.

Более точное выражение, чем (13), можно получить, если не расширять пределы интеграла в (12) до бесконечных. При этом результат выразится через интеграл ошибок комплексного аргумента. Чтобы выразить интеграл через другие функции, выделим в показателе мнимую единицу в явном виде:

R

T = J exp [-Ц1 (r - r1 ^ J r dr =

заданной максимальной числовой апертурой оптического элемента NA :

R

= J exp [iLL (r где

_

r ) 2 ] r d r ,

Y( kra Г

Цr

Ц 2 = i Ц 1 , r = ^°

.

Ц 2

Если в (22) подынтегральный нести за интеграл, то

множитель r = r 0 вы-

T = -7= [Cs (J’ r ) + iSs (,R r)]

_

_

r ₀

где r _a – радиус, соответствующий зоне максимальной

числовой апертуры:

[ R , 7> 1, r = S ^a [ 5 X , Y< 1.

Выражение (26) учитывает тот факт [9], что для фрак-сикона с Y <1 максимальное значение числовой апертуры достигается в центральной части оптического элемента.

Результаты, приведённые в табл. 3, качественно

w cost          f   1 I где Cs (w) = —^dt = cos 1I w,— I,

0                 V ^7

w n z x r sin t ।      - J 1 I

S (w) = ——d t = sin I w,— , s j A t                I     2

0 Ml           V    ^{2 7}

w cost                    w sint cos I (w, V) = J —— dt, sin I (w, V) = J —— dt 0t                               0t

подтверждают аналитические оценки, полученные выше. Хотя при y =2 оказалось лишь примерное совпадение положений фокусов.

Заметим, что использование Гауссовой аподизации апертуры приводит не просто к сглаживанию осевых осцилляций интенсивности, но к потере характерной протяжённости пучка вдоль оптической оси.

Далее сравним поперечное распределение в фокальных плоскостях для двух типов освещающих пучков.

- спиральные функции параметра V от комплексного аргумента w , для которых имеется программа вычисления [13].

Формально спиральные функции параметра 1/2 с точностью до коэффициента равны функциям Френеля, но для комплексного аргумента не имеется стандартных таблиц.

Если не выносить множитель r , то интеграл в (22) равен

2. Анализ поперечного распределения в фокусе

Рассмотрим интеграл (2) в плоскости максимальной

интенсивности при освещении Гауссовым пучком:

k ²

¹ max ( Р ) = — ^Х z max

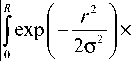
х exp

ikr ²

2 z max

- i (k а0 r )Y

J ₀

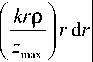
T2 =     [Cs (^"r ) + iSs (^"r )]-

r ₂

2 V Ц2

[ Cs (\r)+S (Т-Г)]+

+ -1— {exp [iLL (R - r2 )21 2 i Ц2 I    L              ]

- exp ( i Ц 2 r ₂ ²

Отметим, что при освещении плоским пучком последнее слагаемое оказывает заметное влияние только в теневой области [9].

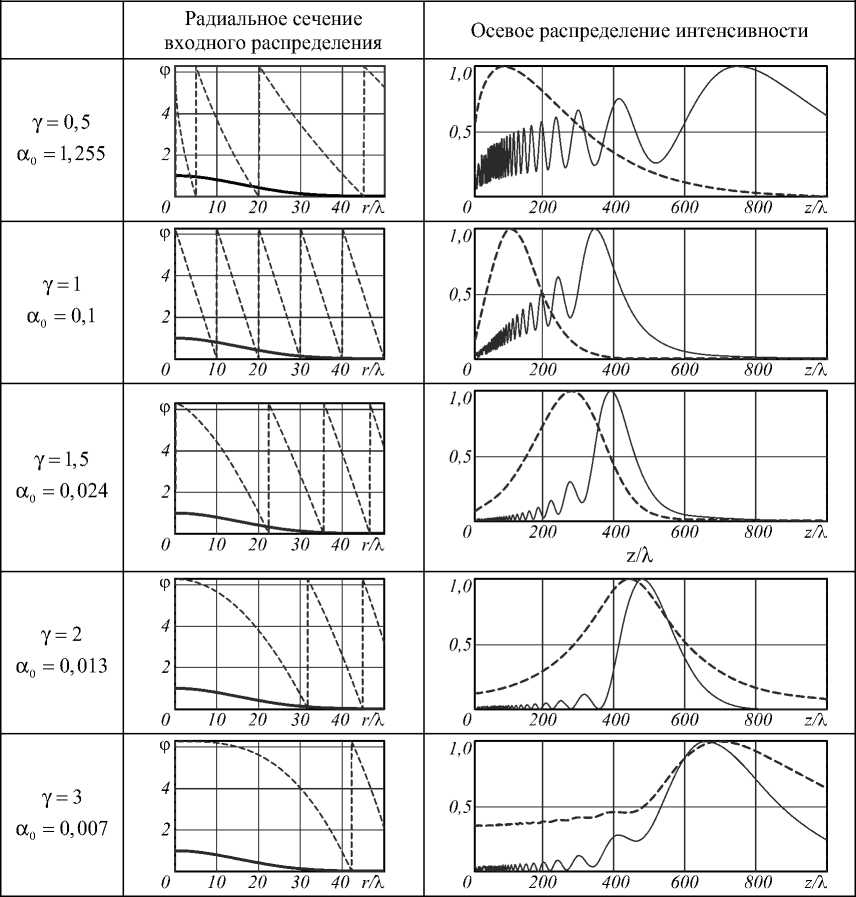
В табл. 3 приведены результаты численного расчёта осевого сечения (3) при использовании различных типов освещающего пучка A ( r ): плоским ограниченным пучком (сплошная линия) радиусом R 50 Л и Гауссовым пучком (пунктирная линия) радиусом о 15 л .

Размер Гауссова пучка был выбран в соответствии с правилом «трёх сигм» так, чтобы на радиусе R была сосредоточена практически вся энергия Гауссова пучка. При больших значениях о часть Гауссова пучка отсекается, и на оси наблюдаются биения, аналогич-

ные освещению ограниченным плоским пучком.

Для оптического элемента (1) рассмотрены значе-

ния у , соответствующие характерным диапазонам. Значения параметра а ₀ выбирались в соответствии с

Учитывая, что о < R /3, предел в (27) можно увеличить до бесконечности. Применяя метод стационарной фазы и используя (12), вместо (27) можно записать:

k ²

¹ max ( Р ) = — z max

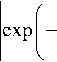
2ц r,2

Ц 1

I exp ( ^- 2 Ц 1 ^r 1² )|^х

и

х

J exp ( ^-Ц 1 ^{r 2} ) exp ( 2 Ц 1 ^r 1 ^r ) J 0 0

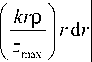
Считая, что максимум находится на оси ( р = 0), представим функцию Бесселя в виде:

J0 (y) = 1 -

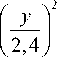
Тогда интеграл, фигурирующий в выражении (28),

можно представить:

и

J exp ( ^-Ц 1 ^{r 2} ) exp ( 2 Ц 1 ^r 1 ^r ) J 0

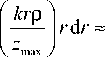
где

= B1

f  k Р

I 2

V ² , ⁴ z max

B ₃ ,

и

B „ = J r ⁿ exp ( -Ц 1 r ² ) exp ( 2 ц 1 r 1 r ) d r .

Таблица 3. Сравнение осевой интенсивности при освещении обобщённой линзы с параметрами, соответствующими максимальной NA =0,1, плоским ограниченным пучком (сплошная линия) и Гауссовым пучком (пунктирная линия)

Выражение (29) равно нулю при р = р ₀ :

Ро =

2,4 z max    B 1

k      B ₃ .

e ^{- x} ( 1 erfc( x ) = —^1 —

V П I x

^^^^^^e

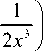
Воспользуемся табличным выражением для (31) [14]:

то получим приближённое значение для радиуса нулевого значения (32) в виде:

и j x" exp (-px2 - qx) dx =

(-1)" п -" Г (q2 '

= exp

2 pp dq" [ P(4p,

2 ^

где erfc( x ) = —= j exp( - t ² ) d t .

V n

x

erfc

( YI .     1,

Если выполнить дифференцирование в (33) и приближённо заменить функцию erfc( x ) начальной частью её асимптотического разложения:

Р о

2,4 z max 2 p k 3

После подстановки значения p из (30) и (12) полу-

чим значение радиуса центрального пика в явном виде:

2 4 z

, max

^{Р о}   V3 k О   4 1 ⁺

(2 -Y ) k

2 z max

I О4 .

Это значение удовлетворительно согласуется с результатами численного моделирования (табл. 4). В табл. 4 показаны сравнительные результаты для Гауссова и плоского ограниченного пучка в плоскостях максимальной осевой интенсивности. Поперечный размер светового пятна приведён по полуспаду интенсивности (FWHM).

Таблица 4. Сравнение поперечной интенсивности в фокусе (размер картины 20 λ× 20 λ ) при освещении обобщённой линзы с параметрами, соответствующими максимальной NA=0,1, Гауссовым пучком ( σ =15 λ ) и плоским ограниченным пучком (R=50 λ )

	Фаза обобщённой линзы	Гауссов пучок (негативное изображение)	Плоский ограниченный пучок (негативное изображение)
γ = 0,5 α 0 = 1, 255	( б*о^ ) Ж>гЖ	z m gs ax = 92 λ , FWHM=4,33 λ	z m pl ax = 750 λ , FWHM=7,48 λ
γ= 1 α 0 = 0,1	(^^)	z gs = 115 λ , FWHM=3,62 λ max	z pl = 348 λ , FWHM=3,25 λ max
γ= 1,5 α 0 = 0,024	©	z m gs ax = 280 λ , FWHM=6,22 λ	z pl = 391 λ , FWHM=4,01 λ max
γ= 2 α 0 = 0,013		z m gs ax = 445 λ , FWHM=8,34 λ	z pl = 481 λ , FWHM=4,95 λ max
γ= 3 α 0 = 0,007		z m gs ax = 700 λ , FWHM=13,17 λ	z pl = 663 λ , FWHM=6,52 λ max

Как видно из результатов моделирования, приведённых в табл. 4, наименьший размер фокального пятна в условиях одинаковой максимальной числовой апертуры достигается при использовании линейного аксикона. Причём результат практически не зависит от типа освещающего пучка, т.к. линейный аксикон по всей области оптического элемента имеет одинаковую числовую апертуру. Использование Гауссова пучка вместо плоского приведёт к сглаживанию осевых осцилляций и сокращению протяжённости фокальной линии.

Во всех остальных случаях наличие на оптическом элементе областей с меньшими значениями числовой апертуры приводит к уширению фокального пятна. Однако при этом могут обеспечиваться другие оптимальные свойства. В частности, параболическая линза обеспечивает наилучшую концентрацию энергии в фокальной плоскости, а фраксикон с γ <1 позволяет получить равномерное распределение интенсивности на протяжённом участке оптической оси [9]. На рис. 2 показаны зависимости размера светового пятна по полуспаду интенсивности от расстояния для значений γ из характерных диапазонов .

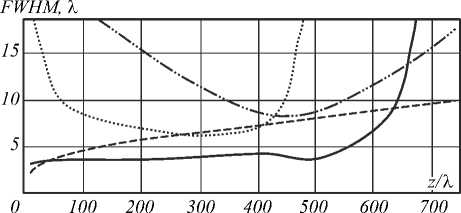
Рис. 2. Зависимость размера светового пятна от расстояния при Y = 0,5 (пунктирная линия), Y = 1 (сплошная линия), у = 1,5 (точечная линия),

Y = 2 (штрихпунктирная линия)

Хорошо видно, что линейный аксикон обеспечивает минимальный размер центрального светового пятна до момента, когда пучок резко расходится.

Фраксикон при γ < 1 формирует пучок с несколько большим размером светового пятна, который, однако, сохраняется значительно дольше, причём уширение пучка происходит очень медленно. Заметим также, что вблизи оптического элемента размер пятна может быть даже меньше, чем для линейного аксикона. Однако этот момент требует дополнительного исследования в рамках более точной модели.

Заключение

Анализ дифракции различных пучков на обобщённой параболической линзе с произвольной степенью с использованием метода стационарной фазы показал, что в этом случае выполняется локальная аппроксимация произвольной фазовой функции оптического элемента линейным аксиконом с меняющимся углом наклона.

Сравнение дифракции на обобщённой линзе Гауссова пучка и ограниченного плоского пучка показало, что подавление осевых осцилляций интенсивности при Гауссовой аподизации приводит в общем случае к сокращению продольной протяжённости фокальной области и уширению размера центрального светового пятна.

Наименьший размер фокального пятна в условиях одинаковой максимальной числовой апертуры достигается при использовании линейного аксикона. Во всех остальных случаях наличие на оптическом элементе областей с меньшими значениями числовой апертуры приводит к уширению фокального пятна.

Преимущество остальных элементов над линейным аксиконом может быть либо в лучшей концентрации энергии в фокальной плоскости, как это обеспечивает параболическая линза, либо в равномерности распределения интенсивности на протяжённом участке оптической оси, что достигается использованием фраксикона со степенью меньше единицы.

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках постановления Правительства Российской Федерации от 09.04.2010 г. № 218: договор № 02.Г36.31.0001 от 12.02.2013. и гранта РФФИ 13-07-97004-р_поволжье_а.