Дифракция гауссового пучка на логарифмическом аксиконе: преодоление дифракционного предела

Интерес к фокусировке лазерного света в продольный осевой отрезок, в том числе с субволновым диаметром, не ослабевает. В [1] c помощью фемтосекундного лазерного импульса с длиной волны λ = 800 нм экспериментально с помощью аксикона сформирован пучок Бесселя, который проделал в стекле наноканал диаметром 200 нм = 0,25 λ и длиной 30 мкм. В [2] экспериментально с помощью сужающейся труб ки (фактически это полый аксикон) из стекла сформировали на расстоянии 2,2 λ фокусное пятно c диаметром, близким к дифракционному пределу FWHM = 435 нм = 0,65 λ , λ = 671 нм. В [3] алмазным резцом из пластика изготовлен логарифмический аксикон (ЛА) с радиусом 6,5 мм, имеющий фазовую функцию вида S ( r ) = γ ln( a + br ²), где γ , а , b – постоянные, r – поперечная радиальная координата в цилиндрической системе координат. Этот аксикон фокусировал свет от He-Ne лазера в осевой отрезок длиной 10 см и диаметром 10 мкм. В [4] численно показано, что вблизи вершины стеклянного аксикона при определённых параметрах может возникнуть субволновое фокусное пятно диаметром FWHM = 0,30 λ . Заметим, что аналитические выражения для осевой интенсивности при дифракции плоской волны и гауссового пучка на обычном коническом аксиконе были впервые получены в [5]. В [6] впервые рассмотрен ЛА с квадратичной зависимостью от радиальной координаты S ( r ) = γ ln( a + br ²), который был реализован с помощью цифровой голограммы и фокусировал свет в осевой отрезок. В [7] проведено моделирование ЛА и показано, что осевая интенсивность вдоль отрезка в среднем более постоянная, в отличие от конического линейного ак-сикона [5], у которого средняя интенсивность растёт вдоль осевого отрезка.

В данной работе рассмотрена скалярная параксиальная дифракция гауссового пучка на логарифмическом аксиконе, который описывается фазовой функцией, как в [3, 6, 7], но при a = 0. Такой акси- кон фокусирует свет в осевой отрезок, который начинается сразу за аксиконом. Фазовая функция такого аксикона имеет вид S(r) = γ ln(r/σ) и имеет особенность в начале координат при r = 0. В этой точке фаза S(r) стремится к плюс (или минус) бесконечности. Однако эта особенность имеет место только в начальной плоскости при z = 0. В любой другой плоскости (z > 0), при освещёнии такого ЛА гауссовым пучком, световое поле имеет конечную энергию и не имеет особенностей. Приводится явное аналитическое выражение для комплексной амплитуды такого поля в зоне дифракции Френеля. Получена оценка для диаметра поперечной интенсивности, которая обратно пропорциональна параметру -1 2

ЛА γ . То есть при достаточно большом | γ | >> 1 можно получить субволновой диаметр лазерного пучка вблизи ЛА. Численны е примеры подтверждают это. Численное моделирование гипергеометрических пучков уже проводилось в работе [8], где также была показана возможность преодоления дифракционного предела с помощью логарифмического аксикона, однако формул для осевой интенсивности и ширины фокусного пятна получено не было.

1. Общее выражение для амплитуды

В скалярном параксиальном приближении рассмотрим дифракцию гауссового пучка на спиральном логарифмическом аксиконе (СЛА) и просто на логарифмическом аксиконе. Функция пропускания в приближении тонкого транспаранта для СЛА в полярных координатах ( r , ϕ ) имеет вид:

T ( r , φ ) = exp

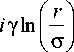
+ in φ

где n – целое число (топологический заряд оптического вихря), γ – вещественное число (параметр «силы» аксикона), σ – параметр масштабирования аксикона. Тогда сразу за СЛА комплексная амплитуда монохроматического светового поля будет иметь вид:

E ₀ ( r , φ ) = exp

-

r

w

. 1 I r I . X

+ i Y ln I — I + in ф l CT )

где w – радиус перетяжки гауссового пучка. Преобразование Френ еля от ф ункции (2) имеет вид:

n + 1                  ^{i γ             n}

(-i)   f z„ If w I f kwp I

E(p,6,z) =           I II I I I x

n! к z ) к CT ) к 2 z )

_- n + 2 + i γ

fn + 2 + iYIk, iz I 2 f „ ikp2I

x ГI             II l--I exp I in 6+       Ix (3)

к 2 )к z ) к 2z )

При получении (6) воспользовались тем, что 1 F 1 ( a , c ; 0) = 1, | Γ (1+ ix )|² = ( π x ) sh^–1( π x ) и arctg( x ) = π /2 – arctg(1/ x ).

На рис. 1 значения осевой интенсивности в нуле ( ρ = 0, z = 0) из (6) равно:

× 1 F 1

n + 2 + i γ 2

2                - 1

; n ₊ 1; -1^E ) f l - iz. )

к 2z ) к z )

где ( ρ , θ ) – поперечные полярные координаты в плоскости наблюдения, z – координата вдоль оптической оси, k = 2 π / λ – волновое число света с длиной волны λ , z 0 = kw ²/2 – расстояние Рэлея, Г( х ) – гамма-функция, 1 F 1 ( a , c ; x ) – конфлюэнтная гипергеометрическая функция [9]. Заметим, что выражение (3) является

I ₀(0) = πγ [ exp( πγ ) - 1 ] ^{- 1} ≥ 1.                      (7)

точным решением параксиального волнового уравнения (типа уравнения Шредингера), и оно является ча-

стным случаем ранее полученного решения для семейства гипергеометрических лазерных пучков [10, 11]. Интенсивность светового поля I ( ρ , z ) = | E ( ρ , z )|², полученная на основе (3), имеет вид:

I ( ρ , z ) =

1 ( n !) ²

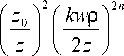
Г f n + 2 + i Y к 2

n + 2

z

x 1l+ - I exp к z )

× 1 F 1

n + 2 + i γ 2

×

I z I

-Yarctg I    | x

к z )

; n + 1; -

-

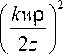
iz

- 1

z

2. Осевая интенсивность

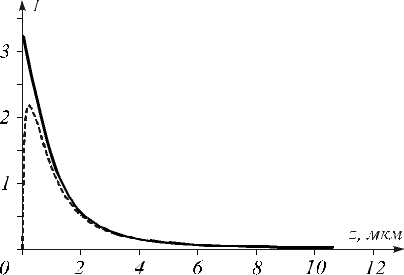
Рис. 1. Осевая интенсивность ( ρ = 0) для собирающего ( γ < 0) ЛА ( γ = –1, w = λ , λ =532 нм), рассчитанная по формуле (6) (сплошная кривая) и на основе интеграла

Рэлея-Зоммерфельда (пунктирная кривая)

Осевая интенсивность на рис. 1 (пунктирная кривая) рассчитана с помощью непараксиального интеграла Рэлея-Зоммерфельда для того, чтобы показать, что, во-первых, параксиальная и непараксиальная осевая интенсивности существенно отличаются друг от друга при z < 2 λ и, во-вторых, параксиальная кривая (сплошная кривая) даёт неправильный результат в нуле I 0 (0) ≥ 1 ( z = ρ = 0).

На рис. 2 показано распределение интенсивности в поперечной плоскости z = 2 λ , полученное с помощью интегралов Рэлея-Зоммерфельда (кривая 1) и Френеля (кривая 2). Остальные параметры моделирования те же, что и на рис. 1.

Заметим, что интенсивность (4) не зависит от масштабного параметра аксикона σ в (1). Интенсивность (4) везде на оптической оси (кроме начальной плоскости z = 0) равна нулю при n ≠ 0. Чтобы рассматривать фокусировку света с помощью ЛА, положим в дальнейшем n = 0. Тогда вместо (4) интенсивность светового поля будет иметь вид:

I 0 ( ρ , z ) = ₂ z ⁰ ₂ z + z ₀

Г f l + i Y к 2

I z» exp -Y arctgI — к z

×

x ^ l + Y ;l;

^{1 l} 2

-

kwp I

2 z )

- 1

_l - iz o | z )

.

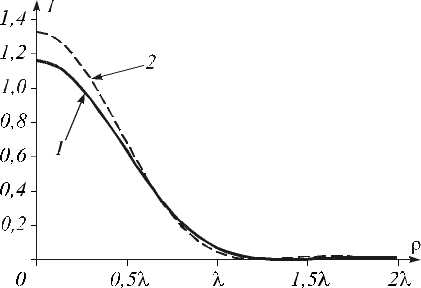
Рис. 2. Интенсивность в поперечной плоскости z = 2 λ ( γ = –1, w = λ , λ =532 нм), полученная с помощью интегралов Рэлея-Зоммерфельда (кривая 1) и Френеля (кривая 2)

Из рис. 2 видно, что ЛА формирует световой пучок почти без боковых лепестков, в отличие от обычного аксикона, формирующего пучок с амплитудой, пропорциональной функции Бесселя J 0 ( αρ ), боковые лепестки которой составляют 0,4 от осевой амплитуды.

Положив ρ = 0 в (5), получим выражение для осевой интенсивности:

т x f nY I    f nY I

I . (z ) = к 2 ) sh ^l к 2 ) ^x

zn2           nY f z x ^—-exP   ^17 arctgI — z 0 + z      _ 2           кz 0

3. Фазовая радиальная сингулярность в центре

Значение I 0 (0) из (7) больше единицы (или равно единице при γ =0), и поэтому оно противоречит выражению (2), из которого следует, что интенсивность в нуле I 0 (0) должна быть равна нулю, так как фаза в начале координат не определена и в любой малой окрестности нуля ( ρ = z =0) содержатся все значения фазы из отрезка [0, 2 π ]. Дело в том, что переход от (5) к (6) возможен при любом z и ρ =0, кроме z = 0. При одновременном стремлении к нулю и z , и ρ результат преобразования выражения (5) будет зависеть от того, с какой относительной скоростью стремятся к нулю обе переменные z и ρ . Например, если устремить к нулю z при фиксированном ρ ≠ 0, то вместо (6) из (5) получим:

В случае, когда ρ строго равно нулю, а z принимает значения, близкие к нулю, вычисление интеграла Рэлея-Зоммерфельда даёт нулевую осевую интенсивность (рис. 1), что можно объяснить неопределённостью фазы в центре начального поля при ρ = z = 0. Однако если в поле (2) устранить фазовую синг улярность в центре, заменив её на плоскую волну с постоянной фазой внутри круга r <  r 0 , т.е. поле (2) заменить на

E0(r,φ) =

exp

-

1, r < r ₀,

r

w

I r I .

+ i Y ln l — I + in ф

I о )

, r ≥ r ₀,

2 ^z I ₀( ρ , z ) = ₂ ⁰ ₂ exp z ₀ ² + z ²

-

2 ρ ²

w ²

I z I

+ 2 Y arctgl— I .

z

При получении (8) воспользовались асимптотическим выражением для гипергеометрической функц ии при x → ∞ [9]:

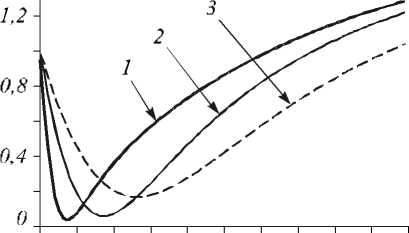
то вычисление интеграла Рэлея-Зоммерфельда даёт единичную осевую интенсивность I 0 (0) = 1, которая быстро спадает в зависимости от радиуса круга r 0 , достигая локального минимума. На рис. 4 показана осевая интенсивность для нескольких значений r 0 : r 0 = 0,01 λ (кривая 1), r 0 = 0,03 λ (кривая 2), r 0 = 0,05 λ (кривая 3).

₁ F ₁( a ; c ; x ) =

Г ( c ) exp( x ) Г ( a ) x^{c - a}

При z = 0 из (8) следует правильное выражение для начальной интенсивности поля (2) I 0 ( ρ , z = 0) = = exp[-2( ρ / w )²]. Выражение (8) верно при z → 0 и ρ ≠ 0. На рис. 3 показан вид ф ункции (8) при ρ , близкой к нулю.

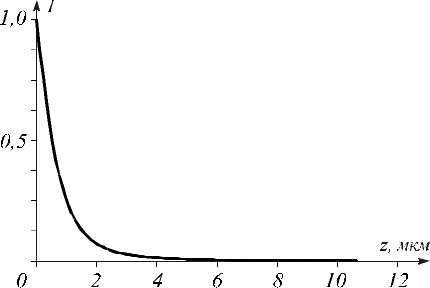
Рис. 3. Зависимость от z интенсивности вблизи z = 0 и при ρ = 0,1 λ ( γ = –1, w = λ , λ =532 нм)

0,5X

Рис. 4. Осевая интенсивность для поля (10)

4. Радиус поперечного распределения интенсивности

Оценим ширину поперечного распределения интенсивности вблизи оптической оси. Известно, что первое приближение координаты x 1 первого нуля гипергеометрической функ ции 1 F 1 ( a , c ; x ) находится по формуле [9]:

На первый взгляд рис. 1 и 3 противоречат друг друг у, но это не так. Так как при z = 0 и ρ = 0 имеет место фазовая радиальная синг улярность (особенность), то есть фаза в (2) и её производная при n = 0 стремятся к бесконечности при r → 0, то это означает, что при z = 0 в центре ( ρ = 0) интенсивность равна нулю I 0 (0) = 0, а в соседних точках ( ρ ≠ 0)

₌     γ c ² - 1,1

^{x 1}    2( c - 2 a ) ,

I ₀ ( ρ ≈ 0) ≈ 1 . Поэтому непрерывным предельным переходом вдоль оптической оси по направлению к точке z = 0 нельзя получить начальную интенсивность I 0 (0) = 1. Но если предельный переход осущ е-ствить при ρ ≠ 0 (рядом с оптической осью), то значение интенсивности при z = 0 получается правильным I 0 (0) ~ 1 (рис. 3).

где γ c –1, 1 – первый корень ф ункци и Бесселя ( с –1)-го порядка: J c –1 ( γ c –1, 1 ) = 0. С учётом (5) в (11) следует подставить значения a = 1+i γ / 2, c = 1, γ 0,1 = 2,4. Так как величины a и x в нашем случае комплексные, то формулу (11) следует понимать для модулей комплексных чисел:

x 1

γ

2 c - 1,1

2 c - 2 a

Тогда вещественную координату первого комплексного нуля (локального минимума) ρ 1 интенсивности (5) можно оценить с помощью выражения:

ρ ₁ = 2,4 w

1 + ^{z 2}2 z ₀

1/4

2(1 + γ ² )

Из выражения (13) след ует, что при больших параметрах гамма | γ | >> 1 зависимость эффективного радиуса поперечного распределения интенсивности будет пропорциональна ( z <<  z 0 ):

• - 1/2

• 5. Моделирование FDTD-методом

ρ ₁ ≈ 2 w γ    .                                 (14)

Из (13) также следует, что выбором достаточно большого значения | γ | ( γ < 0) можно с помощью ЛА получить вблизи плоскости z = 0 световое пятно с любым малым субволновым диаметром. Например, при w = λ , z 0 = kw ²/2 = πλ , z = λ и γ = –400 можно получить световое пятно с диаметром по полуспад у интенсивности FWHM = ρ 1 = λ /10. Это следует из того, что градиент фазы (1) при n = 0 равен γσ /r и стремится к бесконечности при r → 0. То есть ЛА не только собирает на оптической оси распространяющиеся волны, но и возбуждает неоднородные (исчезающие) поверхностные волны с высоким значением проекции волнового вектора на поперечную ось k r >>  k . Наличие таких поверхностных волн вблизи z = 0 обеспечивает субволновые размеры фокусного пятна. Проверим правильность зависимости (14) с помощью моделирования.

Таблица 1. Радиусы поперечного распределения интенсивности

m	1	2	3	4	5
– γ m	1	3	5	7	9
ρ m , λ	2,80	1,93	1,53	1,29	1,13
ρ m / ρ m +1	1,45	1,26	1,19	1,14	–
( γ m +1 / γ m )1/2	1,52	1,29	1,18	1,13	–

В табл. 1: m – номер по порядку; γ m – параметр ЛА; ρ m – радиус в длинах волн первого нуля (или первого локального минимума) интенсивности при z = 10 λ (другие параметры w = 2 λ , z 0 = 4π λ ), численно рассчитанный с помощью преобразования Френеля; ρ m / ρ m +1 – отношение двух соседних радиусов ; ( γ m +1 / γ m )^1/2 – корень квадратный из отношения двух соседних параметров ЛА. В соответствии с (14) значения в третьей и четвёртой строках табл. 1 в каждом столбце должны совпадать, так как ρ m / ρ m +1 = ( γ m +1 / γ m )^1/2. Из сравнения третьей и четвёртой строк табл. 1 видно, что с ростом модуля параметра γ значения этих строк сближаются.

Рассмотрим прохождение радиально-поляризованной моды R-TEM 01 через диф ракцио нный ло-гариф мич еский микроаксикон. Мод елирование провод илось с по мощью метод а R-FDTD [12]. Параметры моделиров ания – размеры области расчёта 20 λ × 20 λ , дискретность разбиения по пространству λ /20, дискретность разбиения по времени

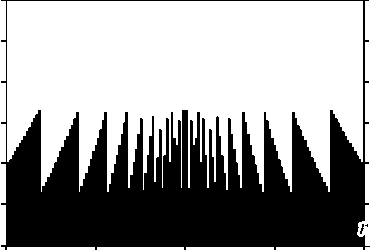
λ /40 c , где с – скорость света в вакууме. Параметры аксикона – максимальная высота h max = λ /( n –1), где n – показатель преломления вещества ( n = 1,5), текущая высота профиля рассчитывалась по формуле X mod [Y ln ( rj o )/( 2 n ) ]/[ 2 n ( n - 1 ) ] , где Y = —20 и σ = 20 мкм, а mod(.) обозначает остаток от д еле-ния . Параметры моды – радиус w = 6 λ , длина волны λ = 532 нм. На рис. 5 показано радиальное сечение ЛА. На рис. 6 – радиально е сеч ение амплитуды освещающего аксикон пучка. На рис. 7 по казано осево е распределение интенсивности, а на рис. 8 – радиально е сеч ение интенсивности в фо -каль ной плоскости (в плоскости с максимальным значением интенсивности).

4 - а)

2 ^^^^JJjiW^kk^^^

-10      -5        0        5        10

. Z, Ц7И

Г, Ц/И

б)

Рис. 5. Логарифмический микроаксикон (а) в вычисляемой области и его увеличенный фрагмент (б) вблизи оси.

На вставке – трёхмерный вид логарифмического аксикона

Моделирование показало, что продольная ширина фокуса по полуспад у интенсивности (рис. 7) FWHM = 2 λ , а диаметр фокусного пятна, находящегося на расстоянии длины волны от «зубчатой» поверхности аксикона, по полуспад у интенсивности равен FWHM = 0,43 λ (рис. 8). Это меньше дифракционного предела FWHM = 0,51 λ . На рис. 8 I = | E |² = | E z |² + | E ρ |², где E z и E ρ – проекции вектора напряжённости электрического поля на продольную и полярную радиальную оси.

Приведём ещё один пример. В этот раз ЛА выберем двумерный и моделирование проводится с помощью программы FullWAVE [13].

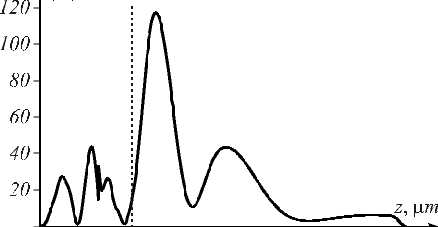
О 2      4      6     8     10

Рис. 7. Распределение интенсивности вдоль оси z (вертикальная линия – линия, на которой лежат вершины рельефа ЛА)

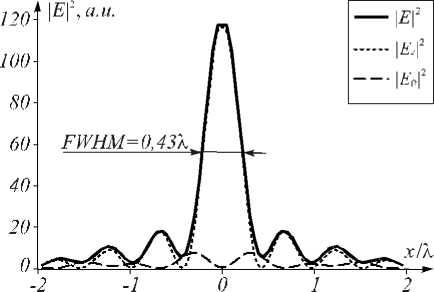
Рис. 8. Распределение интенсивности в фокальном пятне

На рис. 9 показан рельеф двумерного аксикона. Граница области моделирования: [–4 λ , +4 λ ] × × [0, 3 λ ], время моделирования: cT = 30 λ , дискретизация: по x (горизонтальная ось) и по z (вертикальная) – λ /50, по времени – T /100. Высота рельефа: λ /( n – 1) = 2 λ , показатель преломления: n = 1,5, длина волны освещающего света 532 нм, параметры ак-сикона γ = –20 и σ = 4 λ . ЛА освещается гауссовым пучком света с ТЕ-поляризацией и радиусом перетяжки w = 3 λ .

Ширина по полуспад у центрального максимума интенсивности на рис. 10 равна

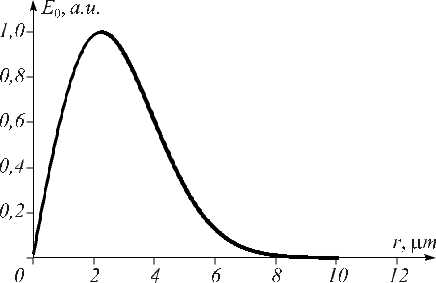
Рис. 6. Радиально-поляризованная лазерная мода R-TEM01

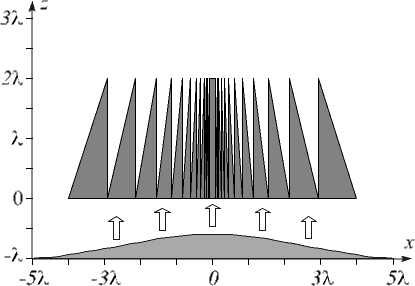
Рис. 9. Вид двумерного ЛА с параметрами: радиус 4 λ , высота рельефа λ /(n–1) = 2 λ , параметр γ = –20

FWHM = 108 нм = 0,20 λ .

Это меньше, чем дифракционный предел в 2D среде FWHM = 0,44 λ / n = 0,293 λ (для стекла n = 1,5).

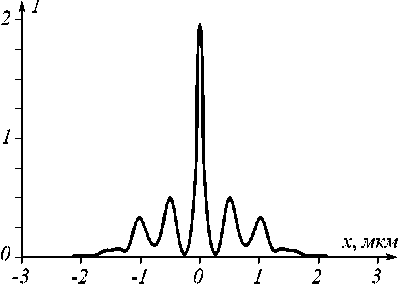
Рис. 10. Усреднённое распределение интенсивности сразу за аксиконом (при z = 2 λ )

Заключение

В работе получены след ующие результаты:

– получено явное аналитическое выражение для комплексной амплитуды св етового поля, опи-сывающ ей в зоне Френ еля дифракцию гауссо-вого пучка на спиральном логариф мическом ак-сиконе;

– получена явная формула для осевой интенсивности в зоне Френеля при дифракции гауссового пучка на логарифмическом аксиконе;

– получена оценочная формула для радиуса дифракционной картины, показывающая обратную зависимость от параметра аксикона γ ;

– с помощью моделирования методом FDTD показано, что на расстоянии z = λ от 3D ЛА с параметром γ = –20 диаметр светового пучка равен FWHM = 0,43 λ , а на выходе 2D ЛА с параметром γ = –20 – FWHM = 0,20 λ (для стекла n = 1,5).

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF PG08-014-1), грантов Президента РФ поддержки ведущих научных школ (НШ-7414.2010.9) и молодого кандидата наук (МК-64571.2010.2).