Дифракция гауссового пучка на спиральном аксиконе

Cпиральный аксикон (СА) и спиральная фазовая пластинка (СФП) были изготовлены по технологии фотолитографии и экспериментально исследованы в 1992 году [1, 2]. СА используется для формирования бездифракционных лазерных пучков Бесселя, а СФП используется для формирования оптических вихрей [1], фазовой микроскопии [2-4] и астрономии [5]. В последнее время возрос интерес к СА и СФП [6-19]. Это связано с тем, что улучшилось качество изготовления пространственных модуляторов света (ПМС), с помощью которых можно теперь формировать дифракционные оптические элементы, в том числе СА и СФП. Так, в [6] с помощью ПМС сформированы СФП высоких порядков ( n >  30) и исследовались оптические вихри высоких порядков. С помощью ПМС можно сформировать составную СФП, которая будет генерировать лазерный пучок, состоящий из нескольких соосных оптических вихрей [7]. Также с помощью ПМС были сформированы бездифракционные пучки Бесселя [8], эллиптические пучки Бесселя [9], пучки Гаусса-Айнса [10] и полые (трубчатые) пучки [11]. ПМС используется для динамического преобразования лазерных пучков, устранения аберраций, выравнивания интенсивности [12-16].

С другой стороны продолжаются исследования СА и СФП, которые изготавливаются по традиционной технологии электронной литографии [17-21]. В [18, 19] экспериментально исследовалась дифракция плоской волны на СФП второго и третьего порядков. В [20] исследовался СА пятого порядка, а в [21] был изготовлен двойной аксикон, который формирует два конических световых пучка, интерферирующих между собой и образующих нулевую интенсивность на оптической оси.

Теоретическое исследование параксиальной дифракции Френеля и Фраунгофера на СФП было проведено для падающих гауссового пучка [22], не- ограниченной плоской волны [2, 18], ограниченной плоской волны [6, 19], эллиптического пучка [23].

Теоретическое исследование дифракции на СА проводилось для неограниченной плоской волны [20]. В [24] исследуется дифракция полихроматического света на СФП. Интерес к исследованию СА и СФП связан также с их применением для манипулирования микрочастицами [6, 14, 20, 25,26].

В данной работе проведены теоретические исследования параксиальной дифракции Фраунгофера и Френеля Гауссового пучка на СА и СФП. Получены новые аналитические выражения для комплексной амплитуды света в виде ряда гипергеометрических функций. Функциональность таких оптических элементов проверена как численным моделированием, так и физическими экспериментами с использованием пространственного модулятора света.

• 2.    Аналитические выражения

Рассмотрим скалярную параксиальную дифракцию коллимированного Гауссового пучка с комплексной амплитудой zx ( r 2 )

E 0 ⁽ r ) = exp l--fl                                   ⁽¹⁾

V w )

на СА, который в приближении тонкого транспаранта описывается функцией пропускания вида тп (r, ф) = exp(iar + гиф)                          (2)

где w - радиус перетяжки Гауссового пучка, ( r , ф ) -полярные координаты в плоскости СА при z = 0, z -оптическая ось, a - параметр аксикона, n = 0, ± 1, ± 2,... - номер СФП.

Тогда параксиальная дифракция волны (1) на СА (2) описывается преобразованием Френеля:

Fn ( Р , 6 , z ) =

ik      |_v ik p 2 | R2 П

- — exp l ikz +     if J exp

2 n z    I 2 z ) oo

-

r ²                  ikr ²

—- + i a r + тф +-- w ²              2 z

- — pr cos ( ф - 6 ) z

rdrd ф ,

где (р, 0 ) - полярные координаты в плоскости z , k = 2 ~/л - волновое число. Используя справочный интеграл [27]

Учитывая связь между гипергеометрической и Бесселевой функциями:

( „ - 1)/ 2

∞

∫ x ^{λ+ 1}exp ( - px ² ) J_v ( cx ) dx =

c v p - ( v +λ+ 2 ) 2   _⎛ v _{+λ+ 2 ⎞}

Γ× 2 ^{v + 1} v !         ^⎜⎝ 2        ^⎟⎠

J(n-1)/2(x)=V2;       „     1 F1| n,n;2ix rf n -1 1 V 2       .

I 2 J

v +λ+ 2

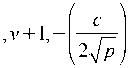
вместо выражения (3) получим:

Fn ( р , 0 , z ) = ( i )— k exp in 0 + ikz + ik^-z                    2 z

f k p 1 n у ( ^{n 1 2 1 2} "  ( i a ) m y m ² f m + n + 2 1

I I                          /                            Г I                       I * (5)

1 2 z )   2 ^{n + 1} n! m = o      m! I 2     )

1 ^F 1

m + n + 2

f , n + 1, -

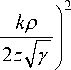
где у = 1/w ² - ik! ( 2 z ) , ₁ F ₁ ( a , b , x ) - вырожденная или конфлуентная гипергеометрическая функция:

/ . \ ГО

1 Fi(a, b, x ) = - m=0

( a )

^{( b )} mm ’

( a ) _m =Г ( a + m )/ Г ( a ) , ( a ) ₀ = 1 , а Г ( x ) - гамма-функция.

Из выражения (5) следует, что картина дифракции представляет собой набор концентрических колец. При р = 0 в центре картины дифракции при

любом n * 0 будет нулевая интенсивность. Так как комплексная амплитуда (5) зависит от комбинации переменных k p ( 2 zр ) , то радиусы p l локальных максимумов и минимумов картины дифракции должны удовлетворять выражению:

2 ¹⁴

wza, I , z_n 1

P l =----- I ^{1 +} 2 I , ^z 0 I z ² I

где a _l - постоянные, зависящие только от номера кольца l = 1, 2,... картины дифракции и параметра α , z ₀ = kw ² 2 - длина Рэлея.

При a = 0 (т.е. аксикон отсутствует), из (5) следует соотношение для комплексной амплитуды дифракции Френеля Гауссового пучка на СФП:

_{(- i )} n + 1 _k

F_n ( ρ , θ , z , α= 0 ) =         ×

z

exp

i ( n θ + kz ) +  ρ

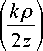
и рекуррентное соотношение для гипергеометрических функций

I n .if d . 1 f n . 1

,F, —, n + 1;2 ix = i --+ 2 . F, —, n ;2 ix ,     (10)

11                     11          ^,

V 2 J V dx J V 2 J

мы можем вместо (8) получить хорошо известное

соотношение для дифракции Френеля Гауссового

пучка на СФП [18, 22]:

E_n ( ρ , θ , z , α= 0 ) =

n + 1              2

( - i )       π ⎛_⎜ z ₀ ⎞_⎟

2      ⎝ z ⎠

×

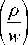
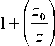
⎡ 3       ⎛ z ⎞ k ρ ² k ρ ² ρ ²

× exp i tan ^{- 1  0} - i + i -+ in θ+ ikz

^⎢⎣ 2 ^⎜ ⎝ z ^⎟⎠     2 R ₀ ( z )      2 zw ² ( z )

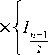
₂ ⎛_⎜ 1     ₊ ik    ⎞_⎟

ρ⎝ w ² ( z )    2 R ₀ ( z ) ⎠

- I_{n + 1}

₂ ⎛ 1 ik    ⎞⎤⎫⎪

^ρ⎜⎝ w ² ( z ) ⁺ 2 R 0 ( z ) ^⎟⎠^⎥⎦^⎬⎪⎭ ^,

где w ² ( z ) = 2 w ² [1 + ( z/z 0 ) ² ] , R 0 ( z ) = 2 z [1 + ( z/z 0 ) ² ] , Iv ( x ) - функция Бесселя второго рода и v -го по-

рядка.

При z ^ да ( z >>  z ₀ ) , из выражения (5) следует соотношение для комплексной амплитуды дифракции Фраунгофера Гауссового пучка на СА ( ₇ = 1 w ²):

F_n ( ρ , θ , z →∞ ) =

_{(- i )} n + 1 _{z 0 ⎛ ik ρ} 2

=         ⁰exp ⎜ in θ+ ikz +

2 ⁿn ! z       ⎝ 2 z

∞ × ∑ m = 0

( i α w ) ^m ⎛ m + n + 2 ⎞ Γ⎜              ⎟×

× ₁ F ₁

m !

m + n + 2

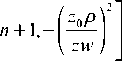
При a = 0 (т.е. аксикон отсутствует) и z ^ го ( z >>  z ₀ ) , из (5) следует выражение для комплексной амплитуды дифракции Фраунгофера Гаус-сового пучка на СФП:

F_n ( ρ , θ , z →∞ , α= 0 ) =

n + 1

- i )    z ⎛             ik ρ ² ⎞⎛ z ρ

⁰exp ⎜ in θ+ ikz +⎟⎜ ⁰

2 ⁿ n ! z      ⎝ 2 z ⎠⎝ zw

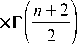
γ -( n + 2 ) 2 ₂ n + 1 n _!

⎛ n + 2 ⎞

^⎜⎝ 2 ^⎟⎠ ^{1 F 1}

n + 2

, n + 1,

-

² ⎛_{⎜ k ρ} ⎞_⎟ ⎝ 2 z γ⎠

+ 2         ⎛ z ₀ ρ⎞

, n + 1, -⎜       ⎟

2           ⎝ zw ⎠

Интересно сравнить выражение (13) с комплексной амплитудой дифракции Фраунгофера плоской

ограниченной волны радиуса R на СФП, когда фокусное расстояние сферической линзы равно f [19]:

( - i ) n ^{+ 1} exp ( in 0 + ikz ) ( kR ² Y kR p ) ( n + 2 ) n!     ^ / J Y f J

1 ^F 2

n + 2

n + 4

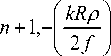
где i F 2( a , b , c , x ) " гипергеометрическая функция:

i F2 ( a , b , c , x )< Z   a T m ^ .

m=0 (b ) m (c ) mm

l^8(p)b

0      0,5    1,0    1,5   2,0 2,5

p, MM

(а)

0      0,5    1,0   1,5   2,0   2,5 p, мм

(б)

>)k

0     0,5   1,0   1,5   2,0   2,5 p, мм

(в)

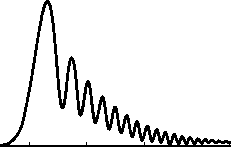
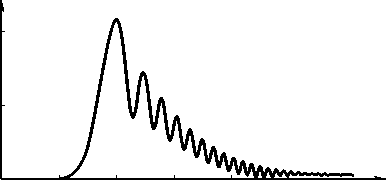
Рис. 1. Радиальный профиль картины дифракции Френеля (амплитуда |F _n ( p , 0 ) на расстоянии z = 200 мм) для Гауссового пучка ( А = 633 нм, w = 1 мм) на СА (n = 8 ): а = 0 мм ¹ (а), а = 20 мм ¹ (б), а = 50 мм ^{- 1} (в)

• 3.    Численное моделирование

0.5         1        1.5                            3 р.тт

В этом разделе моделирование проводилось с помощью (3). На рис. 1 показано рассчитанное распределение амплитуды Fn (p, 0) в относительных единицах как функции радиальной переменной. Эти кривые представляют собой радиальный профиль картины дифракции Френеля (z = 200 мм) Гауссова пучка с радиусом перетяжки w = 1 мм и длиной волны А = 633 нм на СА (n = 8) с параметром а = 0 мм-1 (а), а = 20 мм-1 (б), а = 50 мм-1 (в).

Из рисунка 1 видно, что радиус главного максимума модуля амплитуды увеличивается с ростом значения а .

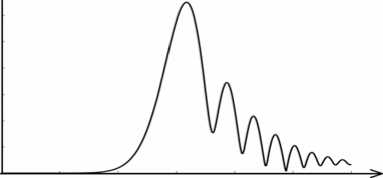
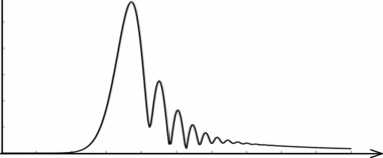
На рис. 2 показаны две рассчитанных радиальных картины дифракции Френеля (амплитуды | F_n ( p , 0 ) ) для Гауссового пучка ( w = 1 мм, А = 633 нм) на СА ( n = 8 ) с параметром а = 20 мм ^{- 1} на расстояниях z = 400 мм (а) и z = 500 мм (б). Из рисунка 2 можно увидеть, что с ростом расстояния z радиус первого на дифракционной картине яркого кольца, характеризующегося максимальной амплитудой, также увеличивается. Сравнение рисунков 1 и 2 дает основание заключить, что радиус первого кольца может меняться либо путем изменения параметра аксикона а при неизменном расстоянии z , либо изменением расстояния z от аксикона до плоскости наблюдения. Отличие будет состоять в количестве периферийных колец (боковых лепестков) на дифракционной картине. Из рисунка 1 в видно, что 13 периферийных дифракционных колец укладываются в радиальный интервал от 1,5 мм до 3 мм. В то же время, на рисунке 2 а в тот же радиальный интервал от 1,5 мм до 3 мм укладываются только семь боковых лепестков, притом, что радиус первого кольца на обеих картинах одинаков.

Л'рЧ

(а)

^.•^1*

0.6

0.5         1.5                                          5 р.тт

(б)

Рис. 2. Радиальный профиль картины дифракции Френеля (амплитуда |F _n ( p , 0 ) ) Гауссового пучка

( А = 633 нм, w = 1 мм) на СА (n = 8 , а = 20 мм ^{- 1} ):

z = 400 мм (а), z = 500 мм (б)

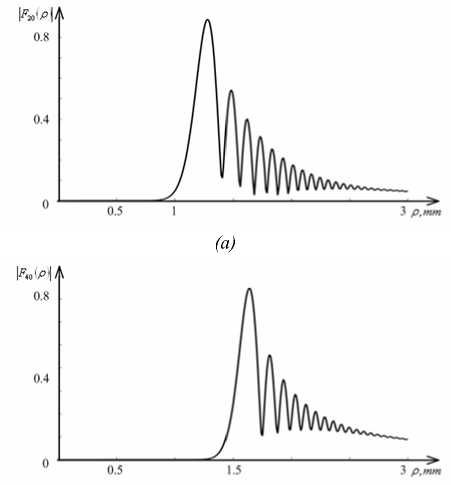
На рисунке 3 показаны две рассчитанных радиальных картины дифракции Френеля (амплитуды |Fn (p, 0) на расстоянии z = 200 мм) Гауссового пуч- ка (w = 1 мм, X = 633 нм) на СА (а = 20 мм 1) разных порядков n : 40 (а) и 50 (б).

Из рисунка 3 видно, что радиус первого кольца на дифракционной картине может быть изменен как варьированием порядка СА п , так и параметра а . Заметим, однако, что в случае рисунка 3, вдобавок к увеличению радиуса первого кольца, увеличение порядка n приводит к утоньшению первого кольца, к большему количеству периферийных колец и к повышенному контрасту коле по сравнению с аналогичными картинами на рис. 1 и 2.

(б)

Рис. 3. Радиальный профиль картины дифракции Френеля (амплитуда \р_п ( р , 9 ) на расстоянии z = 200 мм)

Гауссового пучка ( X = 633 нм, w = 1 мм) на СА

( а = 20 мм ^{- 1} ): п = 20 (а), п = 40 (б)

• 4.    Результаты эксперимента

Простейший способ одновременного генерирования нескольких оптических вихрей с помощью дифракционного оптического элемента (ДОЭ) составить его из двух частей. Центральный круг имеет функцию пропускания СА с дополнительной пространственной несущей частотой, в то время как периферийное кольцо имеет функцию пропускания СА с другой пространственной несущей частотой. Пропускание такого ДОЭ описывается соотношением:

T ⁽ r , ф ) =

exp[z(a r + пф + в cos Ф)]> r < R1, exp[z (a2r + тф - в cos Ф)]> R1 < r < R2,

где p - несущая пространственная частота, R2 - радиус ДОЭ, а R1 - радиус внутреннего круга, который подбирается так, чтобы выполнить условие равных площадей круга и кольца (R1 = R2/V2). Пропускание ДОЭ с радиальной пространственной несущей частотой (вместо уравнения (16) описывается соотношением:

T 2 ⁽ r , ф ) =

exp ( z a ₁ r + гп ф ), r <  R ₁, exp ( z a ₂ r + 1т ф + x p r ), R ₁ <  r <  R ₂.

На рисунке 4 показаны (а) рассчитанная фаза ДОЭ по формуле (16) и (б) картина дифракции Фраунгофера Гауссового пучка на этом ДОЭ (w = 10 мм, X = 633 нм, п = -8, т = 12, число отсчетов N х N = 512 х 512, р = 10 мм-1, а1 = а2 = 0 , R2 = 10 мм, фокусное расстояние f = 150 мм).

(а)

(б)

Рис. 4. Фаза ДОЭ (а) и картина дифракции в задней фокальной плоскости сферической линзы (б)

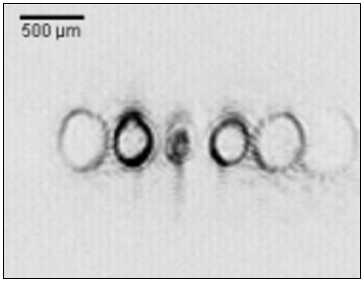
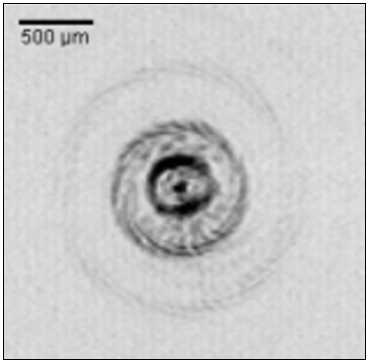
Эксперименты по дифракции Фраунгофера Гаус-сового пучка на СА проводились с помощью программируемого только фазового жидко-кристаллического пространственного модулятора света (ПМС). Пропускание ПМС было пропорционально функции из формулы (16) для СА с п = - 8 , т = 12 и а ₁ = а ₂ = 0 . На рисунке 5 показаны картины дифракции Фраунгофера Гауссового пучка на ДОЭ (16) (а) и ДОЭ (17) (б).

На рис. 5 а видно, что в ± 1 -ом порядке сформировались наиболее яркие кольца, причем, как и на рис. 4 а , левое кольцо ярче, чем правое. Другие порядки дифракции на рис. 5 а возникают из-за нелинейности при передаче фазы (16). На рис. 5 б два соосных кольца из-за взаимной интерференции видны с искажениями.

(а)

(б)

Рис. 5. Картины дифракции Фраунгофера Гауссового пучка на ПМС с функцией пропускания (16) (а) и (17) (б)

Заключение

В работе получены аналитические соотношения для параксиальной дифракции Френеля и Фраунгофера Гауссового пучка на СА и СФП произвольного целого порядка n . Для СА комплексная амплитуда описывается рядом, состоящим из гипергеометрических функций (уравнения (5) и (12)). Для СФП комплексная амплитуда также описывается рядом из гипергеометрических функций (уравнения (5) и (13)). С помощью ПМС были сгенерированы картины дифракции Фраунгофера на составном ДОЭ, формирующем два осевых и неосевых оптических вихря.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF REC SA-014-02), а также гранта РФФИ 05-08-50298.