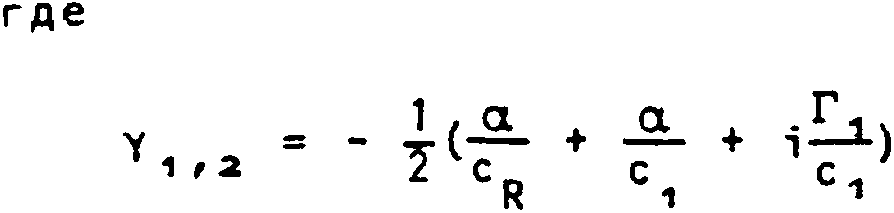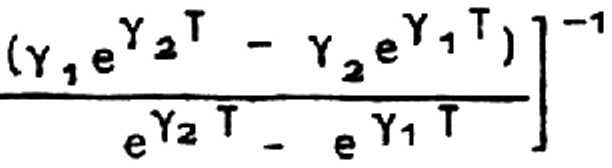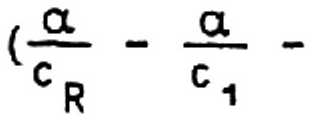Дифракция излучения на синусоидально модулированной многослойной структуре

ДИФРАКЦИЯ ИЗЛУЧЕНИЯ НА СИНУСОИДАЛЬНО МОДУЛИРОВАННОЙ МНОГОСЛОЙНОЙ СТРУКТУРЕ

В [1>2] сообщалось о наблюдении дифракции рентгеновского излучения на многослойной структуре, модулированной поверхностной акустической волной. Для теоретического описания процесса в [2] предложена "кинематическая" модель , для которой характерно пренебрежение ослаблением падающей волны и вторичным рассеянием дифрагированных волн .

Отметим, что подобные структуры представляют интерес и для более длинноволновых диапазонов излучения - оптического, инфракрасного, субмиллиметрового. Получение таких структур для указанных диапазонов вместо использования акустическо го возбуждения требует разработки иных технологий. Например, можно сначала методами компьютерной оптики [з] или голографическим способом получить рельефную решетку, а затем методом напыления наносить на нее нужное число слоев.

Наиболее интересными с точки зрения приложений являются такие случаи дифракции излучения на модулированных многослойных структурах, когда амплитуды дифрагированных волн нельзя считать малыми по сравнению с падающей и "кинематическая" теория неприменима. В данной работе задача решается в "динамическом" приближении .

Рассматривается синусоидально модулированная многослойная структура (см. рисунок), расположенная перпендикулярно оси и содержащая большое количество чередующихся слоев из двух различных материалов, имеющих комплексные диэлектрические проницаемости Е^(1> и е < ²⁾ (I е⁽¹ >-е^{( 21} I« 1 ) и толщины d₁ и d₂ соответственно. Период структуры в направлении оси zi △ =d₁⁺d₂. Границы слоев периодически промодулированы по закону ф(х) = h cos(~x). В [ 1 ,2] эта модуляция вызвана акустическим возбуждением. На структуру падает плоская, линейно поляризованная волна, волновой вектор р которой лежит в плоскости xz, а электрический вектор нормален xz.

Запишем локальную диэлектрическую проницаемость многослойной структуры как функцию координат е = e(x_zz). При h = 0 в не зависит от х и имеет вид комплексной ступенчатой функции e(z), принимающей два значения: Е⁽¹⁾ и е⁽²⁾. Периодиче скую модуляцию структуры будем описывать как зависящий от х сдвиг аргумента в функции е (z):

Е ( X z 2 ) = Е ( 2 — ф (х ) ) .(1 )

Используя подход работ [^,5]. будем разлагать (1) в ряд Фурье, ограничиваясь членами 0-го и ±1-го порядков:

е ₁ f iQCz-фСх)) , -зСКг-фСх))]

е = Е + [е                + еI =

2 I                                       J(

, Ei Г iQz -i Qh cos(Кх) .   - iQz i Qh cos CKx)

= e0 + e e                    + e e, где

Л '

Eq - средняя комплексная диэлектрическая проницаемость.

Используем известное разложение eia cosCb) =  ” ^ j (a)e^m^z                                            ^

ГП т = -оо где J (а) - функция Бесселя т-го порядка, т

Имеем е = , + £± е«И E <т J C-Qh)e^m^x ♦ Ь- e”Oz 1 im J Cahle'"1^.<4)

Используем далее свойства функций Бесселя:

J (-у) = <-1)т d Су), тт

, iQz 7.

е =     + ^ е 2 С-i) J (Qh)e + т=—(

• ♦ |а e'az г im J CQh>e1mKx. 2т

т = -со

Подставим (5) в скалярное уравнение Гельмгольца для амплитуды Е электрического поля и аналогично работе £б] будем искать решение в виде: . -*-*       00               - i о г

Е = R(z)e'1pr + S s (z)e m z                                              (6> m=-”

где г - радиус-вектор;

• p - волновой вектор падающей волны;

• □  = р * Qe + mKe :

• т                 z           х ’

ех и ez - единичные векторы в направлении осей х и 2.

Медленно меняющиеся амплитуды R.(z)z s.Cz), s Cz) относятся соответственно v        m к падающей волне, зеркально отраженной волне, волне m-го порядка дифракции рельефной решетки. В соответствии с подходом [6], члены с экспонентами, не содержащимися в (6), отбрасываем как соответствующие "сильно небрэгговским" волнам; коэффициенты при оставшихся экспонентах приравниваемом членами со вторыми про- изводными от медленно меняющихся амплитуд пренебрегаем.

где

В результате получим

CR

ст

с

е

R о

о

с

а

систему

уравнении связанных волн

^ * aR

9s эГ* to

С т

4е£

Е ( т = -«

пг sm

о _mz

т + 1

J (Qh)s т т

т+1 ^е₁ В

4е о

J

Г

т

= Ь^1'₽г

действительная часть е0;

частота излучения;

скорость света;

коэффициент поглощения:

С7)

о ‘с’’ о с

~)ае0 = Pa-2iae

Условия на границах аналогичны условиям для случая отражательных голограмм в [6] : R СО) = 1, s (Т) = 0, где Т - толщина структуры. Френелевское отражение на границах структуры не учитывается.

Характерной особенностью системы (7)*(8) является то, что энергообмен между s осуществляется только через волну R, а члены, связанные с непосредственным m энергообменом между s , отсутствуют. Физической причиной этого, по-видимому, ш служит отсутствие в первом приближении прошедших порядков дифракции для синусоидальной модуляционной решетки, поскольку волнообразно изогнутые равнотолщинные слои будут давать фазовую модуляцию для отраженной, но не для прошедшей волны.

Из "кинематической" модели [2] следует, что если угол между векторами aQ и о1 существенно превышает ширину угловой селективности многослойного зеркала и угол падения выбран так, что условие синхронизма выполняется для одной из волн sm' то амплитУАы остальных дифрагированных волн будут малы. При отбрасывании этих волн из (7)-(8> остается система двух связанных уравнений, которая в случае синхронизма волны so будет аналогична уравнениям связанных волн Котельника [б] , а при синхронизме s1 или s_1 будет лишь незначительно отличаться от нее. Решение системы проводится так же, как в [6] для случая отражательных голограмм.

Выпишем ответ для наиболее важного случая, когда условие синхронизма выпол няется для волны s1:

s (0) 1

J (Qh) 4ео 1

^)2 с,

e202J2(Qh)

4е * с с о R 1

В заключение отметим, что перспективы использования модулированных многослой ных структур в различных волновых диапазонах обусловлены их высокой спектральной и угловой селективностью, а также тем, что они способны направлять все излучение в заданный порядок дифракции. Представляет интерес отсутствие дифракционных порядков в прошедшем сквозь структуру излучении, что не имеет места у решеток других типов [?] .

Авторы благодарят А.И. Ерко за полезные обсуждения, а М.А. Зуева - за сделанные замечания.