Дифракция плоской волны конечного радиуса на спиральной фазовой пластинке
Автор: Котляр В.В., Хонина С.Н., Ковалев А.А., Сойфер В.А.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 28, 2005 года.
Бесплатный доступ
Получены аналитические выражения через гипергеометрическую функцию, описывающие дифракцию Френеля и Фраунгофера плоской волны конечного радиуса на спиральной фазовой пластинке (СФП) любого целого порядка. Экспериментальные картины дифракции, полученные с помощью СФП, изготовленной на резисте прямой записью электронным лучом, находятся в хорошем согласии с расчетными распределениями интенсивности.
Короткий адрес: https://sciup.org/14058681
IDR: 14058681
Текст научной статьи Дифракция плоской волны конечного радиуса на спиральной фазовой пластинке
Спиральная фазовая пластинка (СФП) как оптический элемент, функция пропускания которого пропорциональна exp ( in ф ) , где ф - полярный угол, n - целое число (порядок СФП), был изготовлен и проанализирован впервые в [4].
В последнее время интерес к СФП возрос, особенно из-за возможности оптической манипуляции микрочастицами с помощью СФП [3, 5-8, 10, 11]. Поэтому актуальным является продолжение исследований дифракции света на СФП. В [6] теоретически исследован случай дифракции неограниченной плоской волны на СФП с произвольным целым n , в [2] теоретически исследована дифракция плоской неограниченной волны на СФП с дробным номером n . Дифракция Гауссова пучка на СФП была исследована в [9].
В этой работе приводятся аналитические выражения для дифракции Френеля и Фраунгофера плоской волны конечного радиуса на СФП произвольного целого порядка. Приводятся также результаты экспериментов по дифракции плоской волны конечного радиуса на СФП с n = 2,3. СФП были изготовлены с высокой точностью (около 1,5% для СФП второго порядка и 4,3% для СФП третьего порядка) с помощью прямой записи электронным пучком на резисте и имеют 32 градации рельефа. Показано также, что экспериментальные картины дифракции хорошо согласуются с расчетными.
Пусть плоская волна (1) падает на СФП, функция пропускания которой имеет вид:
т ( ф ) = exp( in ф ), n = 0,1,2,..., (3)
где ( r , ф ) - полярные координаты при z = 0. Картина дифракции Фраунгофера плоской волны (1) на СФП (3) формируется в задней фокальной плоскости сферической Фурье-линзы с фокусным расстоянием f и описывается преобразованием Фурье:
г ( m ( - i ) n + 1 к с ^тк к
E n ( Р , 6 ) =---7— exp( in 0 ) J n I — r pl r d r =
f 0 I f )
( - i ) n + 1 exp( in 0 ) kR 2 I kR pl
(n + 2) n! TI ) X
Г . \2
„ n + 2 n + 4 . I kR p 1
। F ------,------, n + 1; - -----
12 2 2 ( 2 f )
где ( p , 0 ) - полярные координаты в Фурье-плоскости, Jn ( x ) - функция Бесселя n -го порядка первого рода, 1 F2 ( a , b , c ; x ) - гипергеометрическая функция:
-
( a ) m x m
-
( b ) m ( c ) m m !,
да
1 F,( a, b, c; x) = £ m=0
где
(a)m = a(a +1)(a + 2)...(a + m- 1) = Г(a + m)/r(a) -
1. Дифракция Фраунгофера ограниченной плоской волны на СФП
символ Похгаммера, ( a ) 0 = 1. Уравнение (4) было
Рассмотрим дифракцию Фраунгофера плоской волны конечного радиуса на СФП. Плоская волна единичной амплитуды с радиусом R и волновым числом к = 2 л/Х , где X - длина волны, распростра
получено на основе справочного интеграла из [1].
С учетом того, что функция Бесселя представима
в виде ряда
няющаяся вдоль оси z
амплитудой при z = 0 :
I r 1
E„ ( r ) = circl — , 0 I R )
описывается комплексной
да
Jn (x ) = Z
m = 0
/ 1 \ m / X 2 m + n
x l , m!(m + n)! ( 2 )
из уравнения (4) при n = 0 (СФП отсутствует) следует выражение для дифракции Фраунгофера плоской волны на круглой диафрагме радиуса R :
где
circl ( x )
[ 1, x < 1, [ 0, | x | > 1.
и г \ I — iR 1 Л kR Р Eс(Р) = 1 l J1I —-
I Р ) I f .
Из (4) можно видеть также, что при n ^ 0 в центре Фурье-плоскости ( p = 0) амплитуда равна нулю:
E n ( p = 0, 9 ) = 0 . Из (4) и (5) также следует, что при
малых p<< 2 f/kR 1 F 2 ( a , b , c ; x ) ® 1 и
kR 2 ( kR p) n
E n i n > 0 9 )~ —I — I , где f V 2 f )
~ - знак пропорцио-
столько раз, во сколько раз увеличивается R . Максимальное значение интенсивности на первом кольце растет пропорционально R 4 . Например, для кривых 1 и 3 на рис. 2 отношение максимальных значений интенсивности равно 34/24 ® 5.
нальности. Из (4) можно найти радиус p n кольца (радиус максимального значения интенсивности), приравняв дробь в круглых скобках некоторой постоянной a n , зависящей только от номера спиральной пластинки n :
p n
х к п R
На рис. 1 показаны графики функции интенсивности I n ( p ) = E n ( p , 9 )| 2 , вычисленные по формуле (4). В ряду (5) сохранялось 110 слагаемых. Параметры расчета: X =0,633 мкм, f =100 мм, R =1 мм.
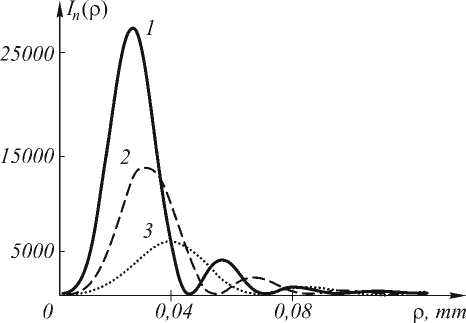
Рис. 2. Радиальные распределения интенсивности картины дифракции Фраунгофера плоской волны на СФПс номером n=2 при R=3 мм ( кривая 1 ) , R=2,5 мм ( кривая 2 ) и R=2 мм ( кривая 3 )
2. Дифракция Френеля ограниченной плоской волны на СФП
Рассмотрим дифракцию Френеля ограниченной плоской волны на СФП. Параксиальная дифракция волны (1) на СФП (3) будет описываться преобразованием Френеля:
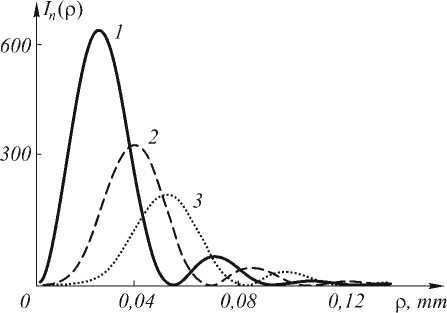
Рис. 1. Радиальные распределения интенсивности картины дифракции Фраунгофера плоской волны радиуса R=1 мм на СФП с номером n=1 ( кривая 1 ) , n=2 ( кривая 2 ) и n=3 ( кривая 3 )
Из уравнения (4) следует, что так как амплитуда En ( p , 9 ) пропорциональна сомножителю p n , то c ростом номера n будет увеличиваться радиус первого кольца картины дифракции (рис. 1). На рис. 2 показаны радиальные распределения интенсивности картины дифракции плоской волны с разными радиусами R на СФП с номером n = 2.
Из рис. 2 видно, что с увеличением радиуса плоской волны R радиус и ширина первого кольца картины дифракции уменьшаются, а максимальное значение интенсивности на кольце увеличивается. Из уравнения (4) следует, что интенсивность пропорциональна выражению:
I n ©~ R Ч2 n х
n+1 1 ( -1 2Л
E (p, 9, z ) = -—-----exp I -^-p- + in9 х n z V
R 2 Л
( ikr | ( k ).
х exp I----I Jn I — rp I r dr=
0 V 2 z ) V z
= exp

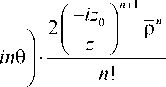
m
( z - I
” 1 J
■y_ V z m=0 (2m + n + 2)!m!
■ 1 F 2
2 m + n + 2
2 m + n + 4
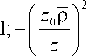
kR2 p где z0 =--- - длина Рэлея, p = . Уравнение (10)
2 R
F 2
n + 2 n + 4
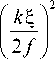
отличается от уравнения (4) тем, что гипергеометрические функции (5) появляются как слагаемые ряда. Из уравнения (10) видно, что при n * 0 в центре пучка при p = 0 имеет место нулевая амплитуда
где ^ = R p . Из уравнений (4) и (8) следует, что с ростом R картина дифракции меняется только масштабно, и радиусы колец уменьшаются во
En ( p = 0, 9 , z ) = 0 при любом z , кроме z = 0 . Из уравнения (10) также видно, что с ростом z в ряду гипергеометрических функций вклад дают только несколько первых членов ряда, а при z ^ да
( z >> z 0 , дальняя зона) вклад в амплитуду будет давать только первый член при m = 0, который совпадает с правой частью уравнения (4). Заметим, что в (10) целая часть отношения z 0 z равна числу Френеля. Заметим также, что выражение (10) при n = 0 (СФП отсутствует) описывает дифракцию Френеля плоской волны на круглой диафрагме радиуса R :
E0 (p, z ) = (-1) exP
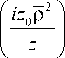
/ . \ m + 1
I ^ I
” I I xX^ z2-m = 0 ( m + 1 ) !
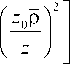
Из (11) можно получить простую зависимость комплексной амплитуды светового поля на оптической оси ( p = 0) от расстояния z до диафрагмы:
E0 (Р = 0, z ) = 1 — exp

Выражение (12) совпадает с полученным ранее [12].
На рис. 3 показаны результаты сравнения эксперимента и расчета. На рис. 3 а показан профиль поверхности СФП с номером n =3 и диаметром 2,5 мм, визуализированный с помощью интерферометра Newview 5000 Zygo (увеличение в 200 раз). Профиль СФП отличается от идеального на 4,3%, а сама СФП имеет 32 градации рельефа и была изготовлена на низкоконтрастном отрицательном резисте XAR-N7220 путем прямой записи электронным пучком с помощью литографа Leica LION LV1 с разрешением 5 мкм.
На рис. 3 б , в показаны экспериментальная и расчетная картины дифракции на СФП плоской волны с радиусом R =1,25 мм и длиной волны X =0,633 мкм на расстоянии z =80 мм. Обе картины дифракции имеют одинаковое число колец (8 колец).
На рис. 4 показан результат регистрации с помощью CCD-камеры картины дифракции Фраунгофера в фокусе линзы ( f =150 мм), полученной для плоской волны с радиусом 1,25 мм, длиной волны 0,633 мкм и СФП с n = 3 .
Относительное среднеквадратичное отклонение теоретических и экспериментальных кривых на рис. 4 б , в составило 14,3%.

(а) (б) (в)
Рис. 3. Профиль поверхности СФП ( n = 3 ) ( а ) , картина дифракции Френеля плоской волны с радиусом R=1,25 мм и длиной волны X =0,633 мкм на расстоянии z=80 мм от СФП: эксперимент ( б ) и теория ( в )
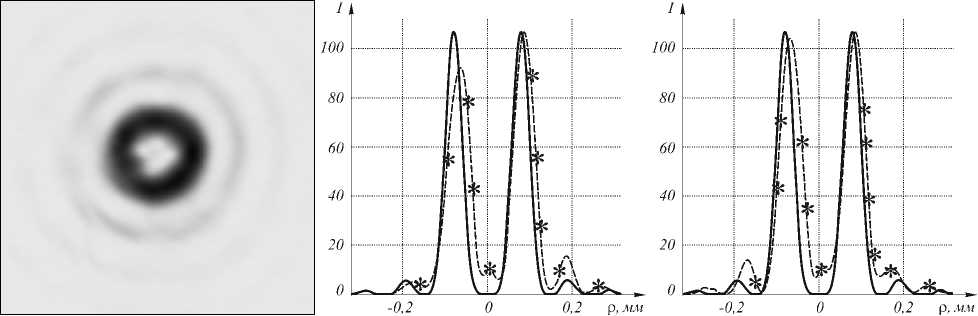
(а) (б) (в)
Рис. 4. Картина дифракции Фраунгофера на СФП с номером n = 3 плоской волны с радиусом 1,25 мм и длиной волны 0,633 мкм, сформированная в фокальной плоскости Фурье-линзы с фокусным расстоянием 150 мм: распределение интенсивности ( негатив ) ( а ) , вертикальное ( б ) и горизонтальное ( в ) сечения интенсивности (------ теория, -- *— *—эксперимент )
Заключение
Итак, мы получили аналитические выражения, описывающие параксиальную дифракцию ограниченной плоской волны на СФП. С помощью изготовленной с высокой точностью СФП с номером n =3 получена экспериментальная картина дифракции Френеля и Фраунгофера. Теория и эксперимент согласуются со средней ошибкой не больше чем 15%.
Работа выполнена при поддержке Министерства образования и науки РФ, правительства Самарской области и Американского фонда гражданских исследований и развития (CRDF Project SA-014-02) в рамках российско-американской программы «Фундаментальные исследования и высшее образование» (BRHE), а также при поддержке грантов Президента РФ МД-209.2003.01 и НШ-1007.2003 (гос. контракт № 02.445. 11.7174), а также грантов РФФИ 05-01-96505 и 05-0850298.


