Дифракция плоской волны на ограниченной спиральной фазовой пластинке: параксиальная векторная теория

В современных научных исследованиях большое внимание уделяется вихревым лазерным пучкам. Основные причины этого интереса заключаются в повышении точности изготовления оптических элементов, формирующих эти пучки, и в возможности решения с их помощью прикладных задач. В частности, одной из таких задач является манипуляция микрочастицами [1].

Вихревые лазерные пучки формируются при прохождении света через спиральные оптические элементы, простейшими из которых являются спиральная фазовая пластинка (СФП) и спиральный аксикон [2].

Существует множество работ, посвященных анализу дифракции света на спиральных оптических элементах, выполненных в рамках скалярной теории дифракции. В данной работе проводится анализ дифракции на СФП в рамках параксиальной векторной теории. В [3] численно показано, что в ряде случаев заметный вклад дает продольная составляющая электрического вектора, не учитываемая в скалярной теории. В данной работе получены аналитические выражения для продольной составляющей поля.

Для анализа распространения векторного электромагнитного поля вдоль оптической оси в большинстве случаев используются два подхода. Один заключается в вычислении дифракционного интеграла Рэлея [4, 5]. Другой заключается в разложении исходного поля по плоским волнам [6]. К числу менее распространенных подходов относится, например, использование функции Вигнера [7]. Из-за трудоемкости или даже невозможности аналитического вычисления интеграла Рэлея часто используют приближения. Например, широко употребляется параксиальное приближение, использованное и в данной работе.

1. Теория

Рассмотрим дифракционный интеграл Рэлея в цилиндрических координатах [4]:

E , ( p , 9 , z ) = - — x ^xV ’    2 n

x

Я E ( r , P ,0 4^Г ^

R ²              a z

E y ( p , 9 , z ) = - 1- ^x 2 П

x

^:ff E y ^{( r} , ^P ’ ⁰⁾^ R ²              °z

L

r d r d p ,

d exp ( ikL )

L

r d r d p ,

E z ( p , 9 , z ) = ±J f| E x ( r , _Ф ,0 )А Г exp^l 1

2 n d x R

,      . 3 Г exp ( ikL)

+ E_y ( r , p ,0)- -^) a y

где

L = z ²

+ p ² + r ²

L

r d r d p ,

- 2 p r cos ( p-9 ) ,

L

+

E_x , E_y и E_z – декартовые проекции вектора напряженности электрического поля электромагнитной волны, k - волновое число, ( r , p ) и ( p, 9 ) - полярные координаты в исходной ( z = 0 ) и текущей поперечных плоскостях, z – оптическая ось.

Пусть в плоскости z = 0 сформировано электромагнитное поле с гармонической зависимостью от угловой полярной координаты, т.е.

E . ( r , P ,0 ) = A . ( r ) exp ( in p ) ,

E y ( r , p ,0 ) = A y ( r ) exp ( in p ) ,

где n – целое число (порядок СФП).

Тогда в параксиальном приближении выражения (1)-(3) принимают вид:

• E \ Л n ^{+1 k} _ A ^{ik p} . • A j I

• E, ( p,9, z ) = ( - i ) —exp ----+ in 9 + ikz x

^x                 z 2 z

^{V                7}          (7)

T I k p r I Л J „ l-----l r d r ,

I z 7

x

E ( p , 0 , z ) = ( - i ) n ⁺¹ —expf ^5- + in 0 + ikz )x ' ^v v / z V 2 z               J

л \ ^f ikr ¹_Л I k p r )

^xl Ay ( ^r ) ^exp | -A— J ^Jn l----J ^{r d r} , 0 V ^{2 z} J V ^z J

( ^- i ) n ^k     I ik p ²              I

E_z ( p , 0 , z ) = -—'— —exp l —— + in 0 + ikz Jx

2 z        V 2 z              J

В геометрическом фокусе линзы, т. е. при z = f , полученные выражения упрощаются [8]:

E x y (p, ⁰ , z = ^f ) = ( - ii )

. n + 1 ^kA x

R

„ + 1 ^x

“^

l----l r ² d r - exp ( - i 0 ) J _ A x ( r ) + A ( r

^{V z J}                   0

x exp

cos 0 +

. » ( X • I ikr 1 f k p r I , I

+ A, ( r ) sin 0 1 x exp ---- J„ ---- r d r ,

У v J V 2 z J n V z J I где Jn (x) - функция Бесселя первого рода порядка.

n –го

В случае, когда в плоскости z = 0 расположена спиральная фазовая пластинка (СФП) радиуса R n -го порядка и линза с фокусным расстоянием f , получим выражения:

. , X .       . I r 1 I

A x ( ^r ) = A x ^circ l    J exp | -

V R J v

i r 1          I

A y ( r ) = A y ^clrc l "A J ^exp | -V R J    V

ikr ² )

J ’ ikr2)

"2 ? J ’

где A_x и A_y – комплексные амплитуды плоской волны, падающей на СФП с линзой. Тогда на расстоянии z сформируется электромагнитное поле со следую-

щими составляющими ( E_{x , y} – это либо E_x , либо

. kA

E x_y ( p , 0 , z ) = ( - 1 ) n ⁺1 -x,^ x

z

E ):

y

f ik p² , • a ,     )

x exp-- + in 0 + ikz x

I 2 z                 J

x

^RR     Г ikr ² f 1

J ^exp —l    _f

^J0       ² V ^z f

-

I k p r )

^J n l-----l ^{r d r} , V z J

n \ А n ^k I ^{ik p} , ■ n I E_z ( p, 0, z ) = ( - 1 ) —₂ exp ----+ in 0 + ikz x

' " ' 2 z 2    Ц 2 z             J

I ч ^R Г ikr ² f 1 ^x l ( A x - A ) ^exp ( i ⁰ ) J ^exp-;-|- ,

I                       0      _ ² V ^z J

-

J . x n +1

x

x

R r ikr I 1 ^{xJ exp}_TV z f

-

_r f k p r ) ₂

n -1 l         J ^{r d r}

V z )

-2 i p ( A_x cos 0 + A y sin 0 ) x

R

C ikr I 1 x exp --- —

^J 0     _ 2 V z f

-

T I k p Г I , J n I l r d r

I z J

2R ikp । • A । Г T x exp ----+ in 0 + ikf I J,

V 2 f           ,

n + 1 kAx = ^(- i ) "A

x f

। k p r

n

r dr =

J 0 V f J f ikp2 , • n , exp V -fj+in0 + ikf Jx nj 2-1            -

n ¹ - ^J 0 ( У ) - ² E ^J 2 m ( У ) - y^J n - 1 ( У ) ’

m = 1

xi

n

n = 2 p ,

J j 0 ( t ) d t - 2 E ² J 2 m - 1 ( У ) _- yJ n - 1 ( У ) ,

n = 2 p + 1,

где y = kR p/ f .

E_z ( p , 0 , z = f ) =

(z i T k 2 f ²

m = 1

Г ik p² , • a , exp ---- + in 0 + ikf x

V 2 f         ^J

R

( A x - A ) exp ⁽ i ⁰⁾ J ^J n + 1

R

k p r ) ₂

--- r d r - f ^J

J ° n - 1

R

k p r I 2.

r2dr f J

n

k pr | rdr.

f ^J

Последний интеграл в (15) вычисляется так же как в (14). Для первых двух интегралов также можно получить аналитические выражения для четных значений порядка СФП n , так как для p = n ± 1

J x ² J_p ( cx ) d x =

= c ³

Г                    ( p - 3)/²               •

( 1 ^- p ² ) ^J 0 ( cx ) ^{+ 2} E ^J 2 q ( cx )

_                   q = 1               _

- c ^{- 1} x ^{2 J} p - 1 ( x )^-( P ⁺ 1 ) c - 2 x^J p - 2 ( x ) •

При небольших порядках СФП получаются простые формулы. В частности, при n = 2 :

E xy ( p , 0 , z = f ) =

2 ifA x , y

---2Г x k p ²

I ik p ² . ™ 7 x exp-- + 1 2 0 + ikf x

V 2 f ^J

x

_r | kR p | kR p | kR p n + J 1

⁰ V f J 2 f ¹ V f

E z ( p , e , z = f ) =

1        [ ik p ²               )

- exp       + i 2 e + ikf x

2 k p   ( 2 f          J

E z ( ^{0,0 z} ) = T-f J[ ^A x ( r ) cos Ф+ A y ( r ) ^sin Q]^{x 2 n} R^

2 kR ² f

( A x cos e + A y sin e ) x

d[ exp ( ikL ) x exp ( in Q ) d L --------

L

r ²

L d r d Q =

x J 2

kR p) "Г J

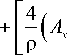
- iA y ) exp ( i e ) -

- 2^p ( A f ^{( x}

cos e + A y sin e )

x

I f [ ^k p

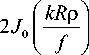
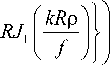
Рассмотрим два частных случая, соответствующих круговой поляризации поля в начальной плоскости.

При A y = - iA x :

iAR    Г ik p ²          )

E z ( p , e , z ) = -f — exp I -f-j + 1 e + ikf Jx

f

x^ 2 - 2 J,

-

kR

- iRJ ₂1 kR ^

2 1 f

.

При A , = A :

E ( p , e , z ) = iA x R exp ik ^p- + i з е + z ⁽      )    f p    I 2 f

ikf I^х

I | kR p ) I      4 f )

x - iRJ + 1 - x

I I f JI    ik p J

xU 2 - 2 J kR ^c

kR p f

^^^^^^B

I kR p p J

¹ 1 f .

.

J

2. Численное моделирование

Вычисление амплитуды на оптической оси проводилось без использования параксиального приближения.

На оптической оси поперечные составляющие (14) при n >  0 равны нулю. Рассмотрим интеграл Рэлея для z-составляющей на оптической оси:

^E z ( ⁰,^{0, z} ) =     JM ^E x ( r , Ф ,⁰ )    ^ exp ^{( ikL} )

2n^Jd             d x

R

L

+ E y ( r , Q ,0 )| ^[ p" d y

+

L

d x d y ,

где L = ( r ² + z ² )^Z .

В случае поля в плоскости z = 0, имеющего вид (5)-(6), и ограниченной апертуры радиуса R :

2n

J exp ( in q ) cos Q d Q n ( 5 n ₊i +5 n -i )

2n

J exp ( in q ) sin Q d Q - i n ( 5 n +i -5 n -i )

1 R л / us x \⁵[ exp ( ^ikL ) = 2 J A x ⁽ r ⁾⁽s n +i +5 n -1 ) d L —

L

iR л ( x \⁵ [ exp ( ^ikL ) - 2 J A y ( ^r )( ⁵ n +1 -⁵ n   , .

где 5 _n - символ Кронекера:

0, n ^ 0,

5 = ,        , n    [1, n = 0.

L

r2dr L rL2dr,

^^^^^^в

Тогда при n * ± 1 амплитуда z-составляющей равна нулю. При n = ± 1 получается, что продольная составляющая электрического поля на оптической оси отлична от нуля:

E z ( 0,0, z ) = 2 x

R xJ[Ax (r) + inAy

(24) r ²d r .

Если использовать вычисление дифракционного интеграла Рэлея методом прямоугольников или трапеций, то на малых расстояниях z значение продольной компоненты устремляется в бесконечность (рис. 1), что не имеет физического объяснения и является следствием неточных вычислений, так как при малых z значение L также становится малым, и подынтегральное выражение в (24) резко возрастает. Поэтому в данной работе использовался другой метод расчета интеграла (24) – численноаналитический.

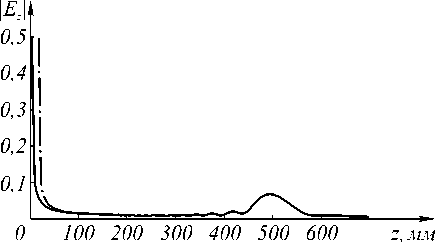
Рис. 1. Зависимость продольной составляющей E_z от расстояния z , рассчитанная с помощью метода прямоугольников (прерывистая линий) и численноаналитическим методом (сплошная линия)

Разобьем интервал интегрирования ( 0, R ) на ( M - 1 ) частей точками r m = mR ( M - 1 ) , m = 0, M - 1 .

Пусть функция g (r ) = r [Ax (r) + inAy (r )]                        (25)

на интервале ( r m , r m _{+ 1} ) аппроксимируется следую-

щим выражением:

где ^kkk . m       m + 1     m

Далее коэффициенты могут быть легко определены например с помощью правила Крамера.

На рис. 2 показано распределение амплитуды z-составляющей электромагнитного поля вдоль оптической оси. Параметры расчета: длина волны: Л = 514,5 нм, радиус апертуры: R = 2 мм, порядок

g ( r ) ” a m + b m r 2 .                                (26)

Тогда

E z ( 0,0, z ) ”

1 M - ² r m + ¹ /      , 2 d[ exp ( ikL )

"2² J⁽ a m ^{+ b} m ^r hr-------

2 m=0 r              дL rm

L

^r d r . L

Рассмотрим два неопределенных интеграла.

I 1 ( ^r Md L

exp ( ikL ) r d    exp ( ikL )

L L r = L

Ii ( r ) = r² —

²          д L

exp ( ikL )

L

— d r = L

= [ L - z²1L + 2 i/k ] exp ( ikL ) .

Тогда

E z ( 0,0, z ) =

M - 2

= 1 E [ a m I 1 (' )l ':, + b . I . ( r )l"¹ ] ■

² m = 0 ^[             m                m ^]

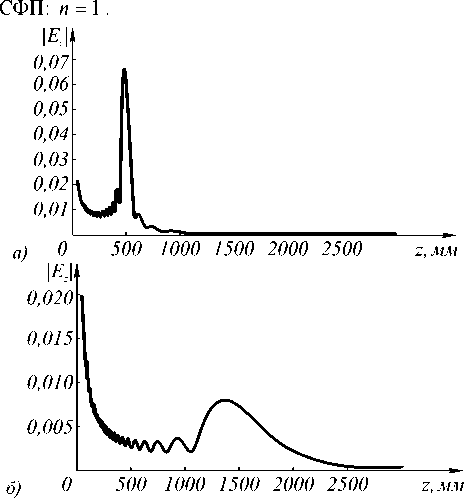
Рис. 2. Значение модуля z-компоненты на оптической оси, рассчитанное для f = 500 мм (а) и f = 1500 мм (б)

Коэффициенты a_m и b_m выбираются по крите-

рию наименьшего среднеквадратичного отклонения от кусочно-линейной функции:

r m + 1

6= J {(am + bmr2 )- rm

[ g - g .11 2

- g m + ^{8m + 1} m ” ( r - r m ) [ d r ^ min, r , - r

[          m + 1     m            ]

где g m = g ( r m ) .

На рис. 3 и 4 показаны распределение амплитуды x- и z-составляющих электромагнитного поля вдоль радиальной координаты. Параметры расчета: длина волны - Л = 514,5 нм, фокусное расстояние линзы - f = 500 мм, порядок СФП - n = 1.

\e2V

Приравнивая нулю производные по a_m и b_m , по-

лучим:

r m + 1

m rm

⁺ b m r 2 ) ^-[ g m ^+A g m ( r ^- r m ) ] } ^d r = ⁰,

r m + 1

J { ( a m ^{+ b} m r 2 ) - [ g m ^{+ A} g m ( r ^- r m ) ] } r 2 ^d r = ⁰,

где ^A g m = ( g m + 1 - g m )/( r m + 1 ^- r m ) .

Тогда a A1 r + b A3 r = mm mm gmgmmmgmm, mm mm

34 g m g mmm g mm ^,

а)

б)

Рис. 3. Значение модуля амплитуды в плоскости z = 500 мм при радиусе апертуры 2 мм: x-составляющая (а) и z- составляющая (б)

ш*

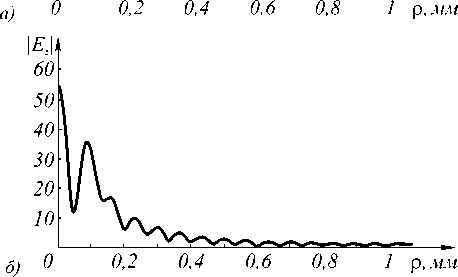
Рис. 4. Значение модуля амплитуды в плоскости z = 500 мм при радиусе апертуры 20 мм: x-составляющая (а) и z- составляющая (б)

Из рис. 4 видно, что z-составляющая амплитуды может составлять несколько процентов, поэтому в ряде случаев имеет смысл учитывать ее наличие, даже в параксиальном случае.

Заключение

В работе были получены аналитические выражения, описывающие параксиальную векторную дифракцию ограниченной плоской волны на СФП. Все три компоненты электрического поля Ex, Ey и Ez представлены в виде конечных сумм функций Бесселя. Показано, что при n=±1 продольная ком- понента электрического поля Ex не равна нулю на оптической оси.

Численно также показано, что в случае параксиальной дифракции продольная составляющая электрического вектора электромагнитной волны может давать вклад величиной в несколько процентов от поперечной.

Работа выполнена при поддержке российско-американской программы «Фундаментальные исследования и высшее образование» (грант CRDF RUX0-014-Sa-06), а также грантов РФФИ 05-08-50298, 0707-97601 и 07-07-97600.