Дифракция плоской волны на пластине из метаматериала при угле падения, равном углу Брюстера или углу полного внутреннего отражения

В последнее время наблюдается значительный интерес к задачам дифракции (рассеяния) электромагнитных волн компактными телами, среда которых представляет собой метаматериал, т.е. искусственно созданную среду. При этом следует отметить, что в настоящее время термин метаматериал используется в нескольких значениях. Первоначально термин «метаматериал» был введен в 2000 г. в работе [1] для среды, диэлектрическая er и магнитная ar проницаемости которой одновременно являются отрицательными величинами - er < 0, цг < 0. Как известно, ранее в работе [2] такую среду назвали средой с отрицательной рефракцией (средой с отрицательным показателем преломления). Позднее в работах, связанных с созданием среды с отрицательной диэлектрической проницаемостью er < 0 и магнитной проницаемостью цг < 0 (или er < 0 и цг > 0), стали также использовать термин «метаматериал». Однако если принять во внимание способ практической реализации подобных ис- кусственных сред, то мы обнаружим, что такие искусственные среды создавались и использовались в антенной технике еще в середине XX века. Например, в широко известной книге Я.Н. Фель-да и Л.С. Бененсона [3] приведены формулы для расчета эффективной диэлектрической er и магнитной цг проницаемости искусственных диэлектриков – композитных материалов, состоящих из диэлектрика с цилиндрическими дырками из воздуха (или воздушными шариками) или диэлектрика с металлическими шариками (цилиндрами). Нетрудно заметить, что именно такие искусственные диэлектрики в настоящее время называют метаматериалом.

Интерес к задачам дифракции (рассеяния) электромагнитных волн компактными телами, среда которых обладает отрицательной диэлектрической проницаемостью er < 0 и магнитной проницаемостью цг < 0, связан с тем, что распространение электромагнитных волн в таком метаматериале сопровождается рядом эффектов, которые не наблюдаются в обычных диэлектриках. Так, еще в 1967 г. [2] В.Г. Веселаго впервые указал на ряд необычных эффектов, связанных с фокусировкой цилиндрических гармонических волн плоским слоем среды с относительной диэлектрической проницаемостью er < 0 и магнитной проницаемостью цг < 0, а также прохождением гармонической волны через призму из та- кой среды. В частности В.Г. Веселаго показал [2], что плоский слой среды с er = -1, pr = -1 позволяет осуществить идеальную (с позиций геометрической оптики (ГО)) фокусировку преломленных и прошедших ГО-лучей, при которой все прошедшие (преломленные) ГО-лучи сходятся в одной точке. Другими словами, плоский слой такой среды преобразует расходящийся фронт падающей цилиндрической волны в сходящийся цилиндрический фронт прошедшей волны. В современной научной литературе такой плоский слой получил название идеальной линзы Веселаго.

Другой эффект, описанный В.Г. Веселаго, – отклонение преломленного ГО-луча в левую сторону от нормали к боковой поверхности призмы из метаматериала e r = - 1, p r = - 1. Рис. 2 иллюстрирует прохождение центрального ГО-луча гауссова пучка через такую призму и диаграмму рассеяния, из которой следует, что пучок отклоняется влево от нормали к поверхности призмы [9]. Именно поэтому среду с отрицательной относительной диэлектрической проницаемостью e r <  0 и отрицательной магнитной проницаемостью p r <  0 часто называют в англоязычной литературе Left Handel Material (LHM) материал.

Первая экспериментальная работа, в которой сообщалось об экспериментальном создании среды с отрицательным показателем преломления, вышла в 2000 г. [1], и тем самым впервые было получено экспериментальное подтверждение эффектам, предсказанным В. Веселаго [2] еще в 1967 г.

Число публикаций, посвященных теоретическому и экспериментальному исследованиям этой проблемы к настоящему времени весьма велико (см. [1–20] и цитируемую там литературу). Отметим, что в большинстве теоретических работ рассматривалась модель плоского слоя [10, 14, 15, 19, 20] (или системы, состоящей из плоских слоев [4, 6]) среды с er < 0, pr < 0 конечной толщины L и с бесконечными границами. Анализ поля цилиндрической (сферической) волны, прошедшей через такую линзу, осуществляется либо на основе представления поля в виде интеграла по плоским (цилиндрическим) волнам в его последующем асимптотическом вычислении методом стационарной фазы. Кроме того, использовалось лучевое описание поля в малоугловом приближении; лучевое приближение, учитывающее прохождение ГО-лучей через слой без их переотражения на границах слоя; приближение тонкого слоя, или приближение Кирхгофа, – то есть фактически на использовании различных вариантов приближенных (асимптотических) методов. Использование строгих численных методов для решения задач дифракции электромагнитных волн на компактных телах из метаматериала ограничивалось случаем, когда размеры тела были соизмеримы с длиной волны [5]. Первые результаты строгого численного моделирования структуры поля в области фокуса линзы Веселаго конечных размеров были получены нами в [7] (см. также [11–13, 16, 17]). Задачи рассеяния плоских и цилиндрических волн компактными телами рассматривались в строгой постановке в работах [8, 9, 16].

В данной работе мы приводим результаты строгого численного решения двухмерной задачи рассеяния поля плоской волны пластиной, среда которой представляет метаматериал с потерями. Полученные результаты интерпретируются с позиций геометрической оптики (ГО).

Рассмотрим двухмерную задачу рассеяния цилиндрической Е поляризованной волны U0(r, Ф):            _____________________________ и0(r,Ф) = H02)(k^r2 + R02 - 2rR0 cos(ф - Фе)) (1)

одиночным диэлектрическим цилиндром, контур поперечного сечения p S ( ф ) которого в цилиндрической (полярной) системе координат описывается уравнением:

P S ( Ф ) = ,              ¹                 .     (2)

pj [cos( ф ) / a ] ^p + [sin( ф )/ b ] ^p

Считается, что среда такого рассеивателя имеет относительную диэлектрическую проницаемость e _r <  0 и относительную магнитную проницаемость p r <  0, т.е. представляет собой метаматериал с отрицательным показателем преломления n_r = -^ | е_г 11 p _r | - i v (где величина v – характеризует потери среды).

Отметим, что, придавая в (2) параметру p различные значения, мы можем изменять форму контура p _S ( ф ), начиная от круглой (когда p = 2 и a = b ) до прямоугольной (когда p >>  1, например при p = 20).

Входящие в выражения (1) – (2) величины представляют собой: { г , ф } - пространственные координаты точки наблюдения в цилиндрической системе координат; { R ₀, ф ₀ } - пространственные координаты точки расположения источника Q волны (нить магнитного или электрического тока) в цилиндрической системе координат; k – волновое число вакуума (свободного пространства); H0²⁾( * ) - функция Ханкеля второго рода и нулевого индекса.

Представим полное поле U ( г , ф ) вне рассеивателя (2) в виде суперпозиции поля падающей волны (1) и рассеянного поля U 1 ( r , ф ):

и ( r , ф ) = H 0²⁾ ( k^r² + R 02 - 2 rR 0 cos( ф - Ф 0 )) +

+ U 1( r ,ф}, а поле внутри метаматериала обозначим соответственно U2( r ,ф).

Известно, что поля U ( r , ф ), U ₂( r , ф ) должны удовлетворять соответствующим уравнениям Гельмгольца вне рассеивателя (2) и внутри него, а также соответствующим граничным условиям на контуре p S ( ф ) рассеивателя (2), заключающимся в непрерывности полей U ( r, ф ), U ₂ ( r, ф ), непрерывности их нормальных производных и условию излучения на бесконечности (условию Зоммерфельда) - т.е. являться решением граничной задачи. Для получения численного решения такой граничной задачи мы воспользуемся модифицированным методом дискретных источников (ММДИ) [21, 22], который позволяет получить решение граничной задачи с контролируемой точностью. Используемое в этом методе представление для полей U 1 ( r , ф ) и U ₂( r , ф ) в виде суперпозиции полей вспомогательных источников цилиндрических волн, расположенных на вспомогательных контурах р_{г х}( ф ), р ^ ₂( ф ) внутри и вне соответствующих контуров 2D структур, заведомо удовлетворяет уравнениям Гельмгольца и условию Зоммерфельда.

Амплитудные коэффициенты для полей вспомогательных источников в методе ММДИ находятся из условия выполнения граничных условий в N точках контура p S ( ф ).

Точность решения задачи контролируется путем вычисления невязки граничных условий в точках, расположенных в середине между точками, где граничные условия выполняются точно (в таких точках граничные условия выполняются наихудшим образом).

Поскольку метод ММДИ и техника его применения к ряду задач с аналогичной конфигура- цией контура рассеивающего тела описан достаточно подробно в работах [21, 22], мы не будем обсуждать особенности его применения в рассматриваемом случае, а лишь укажем, что приведенные ниже результаты расчетов диаграмм рассеяния имеют максимальную невязку граничных условий, не превышающую величины А < 10-3 для любой точки соответствующих контуров.

Исследуем сначала ситуацию, при которой плоская волна имеет угол падения 0 = п /4 на грани квадратной пластины из метаматериала, равный углу Брюстера 0 _О. Для этого рассмотрим следующую задачу. Пусть источник цилиндрической волны расположен в пространственной точке с координатами: kR ₀ = 400 п ; ф ₀ = п /4. При таком положении источника мы имеем ситуацию, при которой волна, падающая на квадратную пластину («электрический» размер стороны равен: 2 ka = 30 п ), имеет плоский фронт. Углы падения плоской волны 0 на верхнюю и правую боковую стороны квадрата при этом равны: 0 = п /4. Пусть среда метаматериала такой пластины имеет относительную диэлектрическую и магнитную проницаемости, среды которого равны: s r =- 5/4, ц _г =- 0,5; потери: v = - 0,001. Тогда углы падения на освещенные грани квадрата равны углу Брюстера: 0 = 0 ₀ = 45 ° .

Хорошо известно, что в случае падения такой плоской волны на бесконечную плоскую границу раздела такой среды и свободного пространства мы не должны иметь отраженной волны. В случае компактного рассеивателя, когда плоская поверхность, от которой происходит отражение плоской волны, имеет конечный размер, ситуация значительно усложняется.

а)

Рис. 1. Структура ближнего рассеянного (а) поля и полного (б) поля при угле падения 0 плоской волны на верхнюю и правую боковую грани квадратной пластины, равной углу Брюстера 0 = 0 ₀ = 45 °

б)

На рис. 1 a, б представлен результат расчета пространственного распределения амплитуды рассеянного поля и полного поля внутри квадрата и его окрестности соответственно. Из результатов, представленных на рис. 11, следует, что поле внутри пластины образует две области – область света и область тени. Область света состоит из двух подобластей, форма которых напоминает форму прямоугольного треугольника. Каждая такая подобласть прилегает одной своей стороной к верхней освещенной стороне квадрата и правой боковой освещенной стороне квадрата соответственно. При этом такие треугольные подобласти имеют общую площадь перекрытия, прилегающую к освещенному с двух сто- рон углу квадрата. Внутри общей площади наблюдается интерференционная структура поля, и она отсутствует вне нее. Область тени занимает остальную часть квадрата, и амплитуда поля в ней близка к нулю, причем наблюдается размытие границы свет – тень. Кроме того, на рис. 1 а мы видим, что каждый освещенный угол квадрата является источником цилиндрической (краевой, или дифракционной) волны.

Отметим, что рассеянное поле вне квадрата, но вблизи каждой освещенной грани квадрата отлично от нуля. Кроме того, из каждой освещенной грани квадрата выходит в обратном направлении (с углом, не равным углу падения) пространственно ограниченный пучок поля.

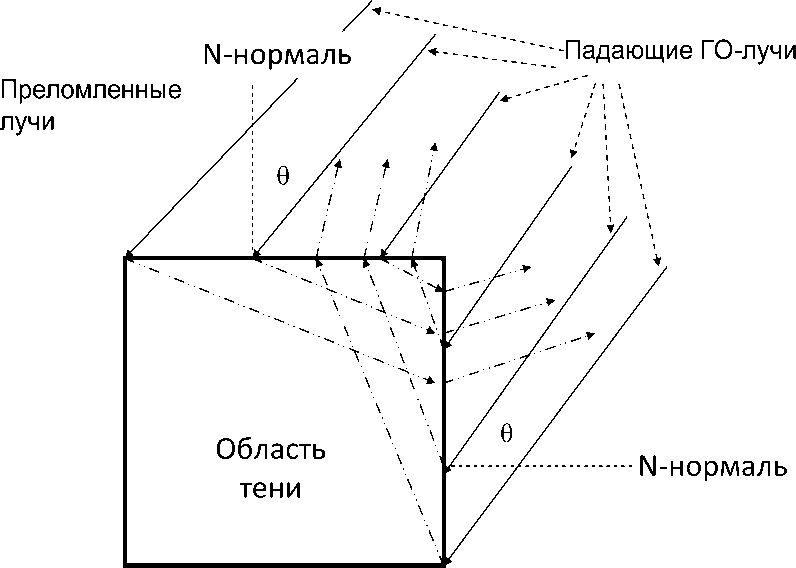
Рис. 2. Взаимодействие ГО-лучей с квадратной пластиной из метаматериала при угле падения 0, равном углу Брюстера 0 = 0 0 = 45 °

Чтобы понять изображенную на рис. 1 структуру ближнего поля, обратимся к картине семейства ГО-лучей, изображенной для этого случая на рис. 2. Из этого рисунка следует, что каждая освещенная грань квадрата не содержит отраженных ГО-лучей, а преломленные ГО-лучи образуют зону тени внутри квадрата. При этом преломленные верхней гранью квадрата ГО-лучи распространяются внутри квадрата сначала не пересекаясь, а затем пересекаясь с ГО-лучами, преломленными правой боковой гранью квадрата. После пересечения такие ГО-лучи попадают на правую боковую грань квадрата и по- сле преломления выходят из нее в обратном направлении под углом, отличным от угла падения. Аналогично ведут себя ГО-лучи, преломленные правой боковой гранью квадрата. Отметим, что преломленные ГО-лучи не попадают на нижнюю грань квадрата. Такая структура семейства ГО-лучей позволяет объяснить результаты расчета пространственного распределения амплитуды рассеянного или полного поля в ближней зоне квадратной пластины, представленные на рис. 1, а также рассчитанную нормированную диаграмму рассеяния (структуру рассеянного поля в дальней зоне), изображенную на рис. 3.

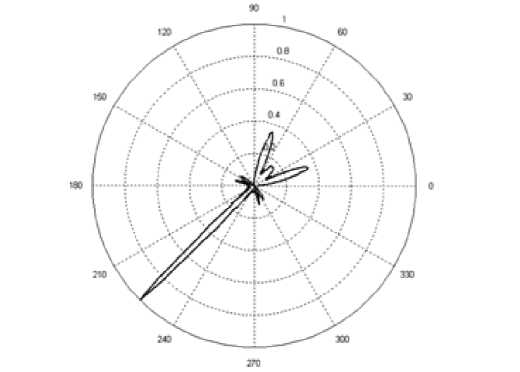
Рис. 3. Нормированная диаграмма рассеяния квадратной пластины при угле падения θ плоской волны на грани квадратной пластины, равном углу Брюстера 0 = 0 0 = 45 °

Таким образом, из представленных результатов следует, что при дифракции плоской волны на пластине с углом падения на грани пластины, равном углу Брюстера, наблюдается слабое отражение поля от верхней грани пластины. При этом наблюдается появление двух дополнительных направлений максимального излучения в обратном направлении. Их появление связано с тем, что ГО-лучи, преломленные верхней гранью пластины (или правой боковой гранью пластины), испытывают повторное преломление правой боковой (верхней) гранью пластины.

Пусть относительная диэлектрическая и магнитная проницаемости среды квадратной пластины («электрический» размер сторон: 2ka =2kb = 30π) равны: εr =-0,5 2, µr =-0,5 2, потери такой среды ν =-0,001. Источник цилиндрической волны имеет пространственные координаты: kR0 = 400π; ϕ0 = π/4. При таком положении источника мы опять имеем ситуацию, при которой волна, падающая на квадратную пластину, имеет плоский фронт. Однако при таких параметрах среды метаматериала угол падения плоской волны θ на верхнюю и правую боковую стороны квадрата равны: 0 = 45° и равны углу полного внутренне -го отражения: θ= θp. Если бы мы имели ситуацию падения такой плоской волны на бесконечную плоскую границу раздела «свободное пространство – метаматериал», то рассеянное поле должно было бы иметь только отраженную волну. При этом преломленная волна должна перейти в поверхностную обратную волну.

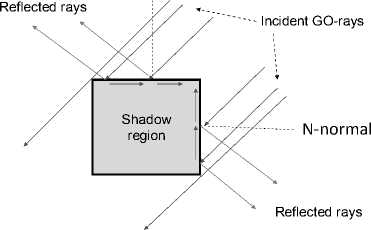
В нашем случае квадратной пластины структура семейства ГО-лучей, падающих на грани квадрата под углом полного внутреннего отражения, изображена на рис. 4. Из этого рисунка следует, что внутри квадрата должна образовываться зона тени, поскольку преломленные лучи становятся поверхностными лучами. Кроме того, из-за существования двух предельных ГО-лучей, освещающих два противоположных угла квадрата, зона тени образуется и за квадратом.

N-normal

Surface rays

angle of incidence-angle of total reflection 45 [degrees]

Рис. 4. Взаимодействие ГО-лучей с квадратной пластиной из метаматериала при угле 9 падения, равном углу полного внутреннего отражения 0 = 0 p = 45 °

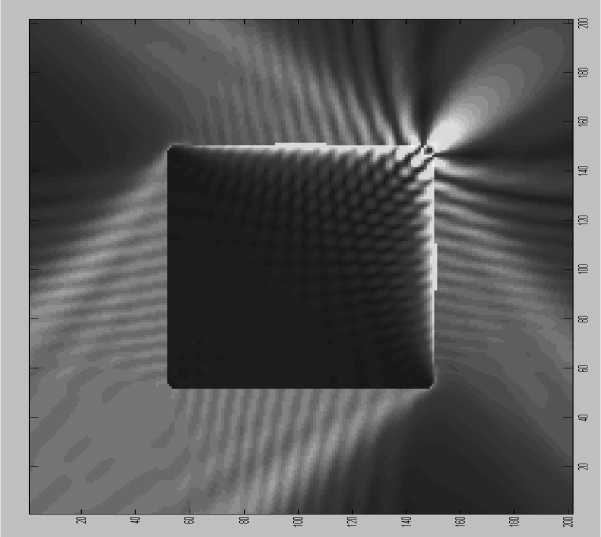
На рис. 5 a, б представлен результат расчета пространственного распределения амплитуды рассеянного поля и полного поля внутри квадрата и в его окрестности. Из результатов, представленных на рис. 5, следует, что внутри большей части пластины поле близко к нулю (т.е. образуется область тени) и отлично от нуля в узкой пространственной области, прилегающей к освещенным граням квадрата. При этом в непосредственной близости освещенных граней пластины видно существование поля обратной поверхностной волны, интенсивность которой убыва- ет при удалении от освещенного угла пластины (см. рис. 5). В окрестности освещенного угла наблюдается часть пространства (подобласть), в которой структура поля имеет характерный вид чередующихся светлых и темных пятен с убывающей интенсивностью. Кроме того, мы видим, что угол, образованный пересечением освещенных сторон, является источником цилиндрической (краевой, или дифракционной) волны, а освещенные стороны квадрата отражают поле падающей волны в направлении угла отражения 9omp = 45".

Scattered field

2ka=60 π

ε r = μ r = -0.5 √2

а)

Full field

ε r = μ r = -0.5 √2

2ka=60 π

б)

Рис. 5. Структура ближнего полного и рассеянного полей прямоугольной пластины при угле падения плоской волны на грани прямоугольной пластины, равном углу полного внутреннего отражения 0 = 0 _р = 45 °

Отметим, что два других освещенных угла квадрата практически не создают краевых (дифракционных) волн. Ясно, что происхождение и характер чередующихся светлых и темных пятен амплитуды рассеянного поля внутри пластины можно объяснить сложением полей краевой волны и обратной поверхностной волны.

Интерференционная структура полного поля вне квадрата хорошо видна на рис. 5 б. На этом рисунке темные и светлые полосы интен- сивности поля располагаются параллельно граням пластины в области, прилегающей к освещенным граням пластины, а в окрестности освещенного угла имеют цилиндрическую структуру. Очевидно, что их происхождение связано с противофазным и синфазным сложением падающего и отраженного (рассеянного) полей.

Результаты расчета нормированной диаграммы рассеяния (дальнего рассеянного поля) иллюстрирует рис. 6. На этом рисунке видно, что рассеянное поле формирует две отраженные волны с углами отражения, равными углу падения (т.е. 9 = 45° οmp          ^.

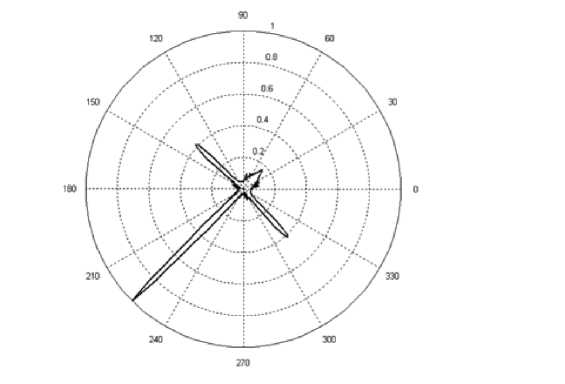
Рис. 6. Нормированная диаграмма рассеяния квадратной пластины при угле падения плоской волны на грани прямоугольной пластины, равном углу полного внутреннего отражения ф0 = в = ва = 45°

Из приведенных выше результатов следует, что процесс дифракции плоской волны на конечной пластине из метаматериала существенно отличается от случая плоской бесконечной границы раздела «метаматериал – вакуум».