Дифракция рентгеновских лучей в кристаллах эллиптического сечения

Цилиндрические кристаллы создаются искусственно для разных физико-химических приложений. Такие кристаллы и микрокристаллы используются как SiGe сердцевины оптических волокон, микрорезные инструменты диаметром до нескольких микрометров и элементы микрооп-тических и микроэлектронных систем. Применяются разные методы для создания цилиндрических кристаллов, включая лазерную рекристаллизацию, обработку сфокусированным ионным пучком и литографию на задней стороне 3D-диффузора. Кроме того, цилиндрические кристаллы выращиваются химическим осаждением из паровой фазы и зонной ростовой технологией с лазерным нагревом.

Динамическая теория дифракции рентгеновских лучей (ДТД) ранее была разработана для кристаллов цилиндрического сечения с использованием метода Римана-Грина [1, 2] и численным интегрированием уравнений Такаги-Топена без учета углового распределения интенсивности рассеяния [2]. При вычислении профилей кривых рассеяния кристалл делился на участки в зависимости от величины угла Брэгга [1]. Такое разбиение кристалла на области не только усложняет процедуру вычислений, но и делает расчеты достаточно приближенными.

В настоящее время для исследования кристаллических структур широкое применение получили методы трехкристальной дифрактометрии [3] и брэгговской когерентной дифракционной визуализации [4,5]. Вычисление карт в об-

S.I. Kolosov, V.I. Punegov

Institute of Physics and Mathematics,

Federal Research Centre Komi Science Centre, Ural Branch, RAS,

Syktyvkar

Using the two-dimensional recurrence relations of X-ray dynamic diffraction, the scattering intensity distribution in elliptical crystals has been numerically simulated. This approach makes it possible to study diffraction in cylindrical structures, as well as in rectangular crystals.

В данной работе впервые рассмотрена возможность вычисления рентгеновских интенсивностей волновых полей и RSM от кристаллов цилиндрического сечения. В случае динамической дифракции применялись двумерные рекуррентные соотношения. Результаты в кинематическом приближении получены на основе аналитического решения.

1.    Динамическая дифракция

Рассмотрим динамическую дифракцию рентгеновских лучей в кристалле цилиндрического сечения (рис. 1 а), при этом выполняется закон Брэгга 2d sin θB = λ, где d — межплоскостное расстояние отражающих атомных плоскостей кристалла, θB — угол Брэгга, λ — длина волны падающего рентгеновского излучения. Дифракция рентгеновских лучей в континуальной среде зависит от Фурье коэффициентов поляризуемости xg = -r о А2 Fg /(nVc). Здесь Fg — структурный фактор, Vc — объем элементарной ячейки, rо = e2/(mc2) — классический радиус электрона, e, m — заряд и масса электрона. Отметим, что коэффициенты а о ,h = nx о ,h/(А sin 6b) в уравнениях Такаги-Топена [9, 10] характеризуют взаимодействие рентгеновских полей в латерально бесконечном кристалле единичной толщины, при этом амплитуды пропускания (рассеяния вперед) r0 и отражения rh от одной атомной плоскости в модели Дарвина связаны с данными коэффициентами как r0h = а0hd. Это означает, что в модели Дарвина вся электронная плотность континуальной среды, заключенная между соседними атомными плоскостями, сосредоточена в бесконечно тонкой решеточной (атомной) плоскости.

Мы исследуем для простоты симметричную дифракцию ст— поляризованного излучения на совершенном цилиндрическом кристалле. Обозначим T _n ^m амплитуду проходящей волны непосредственно перед узлом ( m ; n ) , S — — соответствующее значение амплитуды отраженной волны (рис. 1 а). С учетом динамического рассеяния для отраженных S и проходящих T волн можно записать следующие рекуррентные соотношения [6]:

гр m   -mm— 1 i - m—- 1

Tn +1   tTn + r Sn   , m     m—1     m—1

S n = ^tS n +1 ⁺ rT n +1 ,

где t = t = (1 + r o )exp( iф d ) , r = r h exp( iф d ) , r _= r h exp( iф d ) , r g to — ix g nd/ ( А sin 6 b ) ( g = 0 ,h,h ) , ф d = i 2 nd/ ( А sin 6 _b ) .

Рекуррентные соотношения (1) определяют структуру динамического взаимодействия проходящих и отраженных рентгеновских волн. Для описания дифракции в кристалле заданной формы необходимо исходить из граничных условий.

Пусть на кристалл падает рентгеновский пучок под углом 6 1 = 6b + A6 1 к отражающим атомным плоскостям. При прохождении рентгеновских лучей, как в вакууме, так и в объеме кристалла, происходит изменение фаз рентгеновских волн. За начало отсчета фазовых изменений выберем начало системы координат (x = 0; z = 0, рис. 1). В этой точке амплитуда падающей волны ТО (рис. 1) равна единице. Для рентгеновских волн, фронт которых ограничен вертикальной осью z, разность хода растет с ростом n по закону nd sin 6 1, а разность фаз вдоль вертикального направления изменяется как фП in = (2п/А)nd sin 6 1 Поэтому граничное условие сверху вниз вдоль оси z имеет вид Т0 = exp(iфnin), где n = 0, 1,2,..., Nz. Для верхнего фронта рентгеновских волн, идущего от начала координат и распространяющегося вдоль оси x, разность хода растет с ростом номера узла m как mAx cos 6 1, а разность фаз вдоль горизонтального направления изменяется как ф—in = (2п/А)mAx cos 6 1. Граничное условие на этом участке задается выражением ТЦ = exp(iфmin), где m = 0, 1,2,..., Mx. При выше заданных граничных условиях распространение рентгеновских волн, какв вакууме, так и в объеме кристалла, может быть описано уравнениями (1) с учетом того, что в вакууме rg = 0. Поэтап- но реализуя процедуру рекуррентных вычислений, изложенную в [6], необходимо ввести ограничения, связанные с границами раздела вакуум-кристалл. Рентгеновская волна, распространяясь в вакууме до первого узла кристаллической решетки, претерпевает фазовые изменения, при этом амплитуды отраженных рентгеновских волн от атомных плоскостей, как вперед, так и в направлении дифракции, равны нулю. Вычисления производятся с использованием формулы Т-+1 = ТЦ—1 exp(iфd). Как только эта волна достигает границы цилиндрического кристалла, то с увеличением n и m рекуррентные соотношения (1) будут описывать динамическую дифракцию в объеме цилиндрического кристалла. Это продолжается до тех пор, пока рентгеновская волна не достигнет узел вне кристалла. Далее в соотношениях (1) необходимо снова принять условие rg = 0. Таким образом, вычисления проводятся по всем узлам прямоугольной решетки Mx х Nz с использованием границ раздела вакуум-кристалл. Для цилиндрического кристалла контур его сечения будет удовлетворять условию x2 + z2 = R2, или (Mx Ax/2)2 + (Nzd/2)2 = R2, где R — радиус цилиндра.

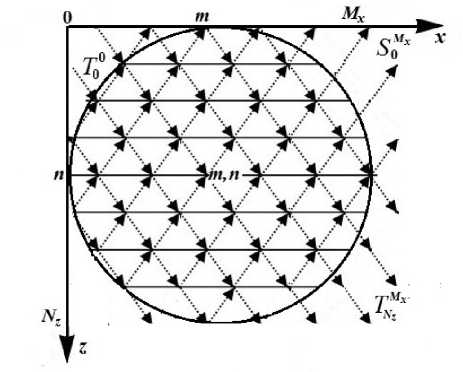
(a)

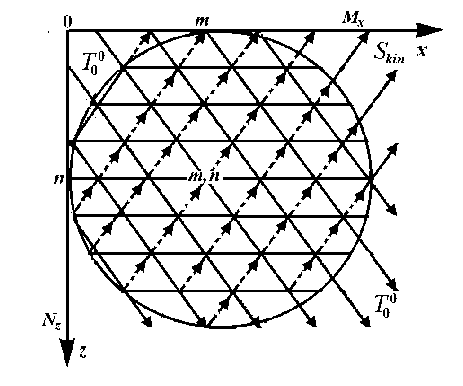
(b)

Рисунок 1. Схематическое изображение динамической (a) и кинематической (b) дифракции в кристалле цилиндрического сечения.

Figure 1. Schematic representation of dynamic (a) and kinematic (b) diffraction in a crystal of cylindrical cross section.

Для фиксированного угла падения рентгеновского пучка на кристалл под углом θ 1 в трехосевой дифракционной схеме регистрируются выходящие (дифракционные и проходящие) пучки под разными углами, например θ 2 . В этом случае возникают дополнительные фазовые изменения рентгеновских волн в вертикальном ф П S = (2 nd/X )[ nd sin 6 2 — M x A x cos 6 2 ] и горизонтальном Ф ms = — (2 nd/X ) m A x cos 6 2 направлениях для отраженной волны S . Процедура расчетов должна быть дополнена граничными условиями для отраженной волны: S _n ⁰ , S _N ^m _z . Интенсивность отражения рентгеновской волны находится из соотношения:

I h ^{( q} x ,^q z ) = ^{|S ( q} x ,^q z ) | =

M x                      N z                  2 ₍₂₎

= | £ S m exp( iф ms ) + £ S M x exp( ф П, s ) | , m =0                n =1

где q x = k sin 6 B (A 6 1 — A 6 2 ) , q _z = —k sin 6 B (A 6 1 + A 6 2 ) . Амплитуды дифракционных рентгеновских волн S mm и S _n ^{M x} вычисляются с использованием рекуррентных соотношений (1).

2.    Кинематическая дифракция

Амплитуда отраженной рентгеновской волны от цилиндрического кристалла в кинематическом приближении вблизи узла обратной решетки может быть вычислена применением рекуррентных соотношений (1) при условии r = 0 и r 0 = 0 . С другой стороны, выражение этого коэффициента может быть представлено в аналитическом виде. Выражение для амплитуды отраженной рентгеновской волны в полярной системе координат запишем как

S kin ( q x ,q z ) = ia h

/   /   exp( iq о p cos ф) pdpdф, где q0 = ^(qxR)2 + [(qz - a0)R]2. Выполняя интегрирование (3) и используя интегральное представление функции Бесселя нулевого порядка

J о ( q 0 p ) = - / exp( iq о p cos ф ) dф, π ₀

получаем аналитическое решение для амплитуды отраженной рентгеновской волны от кристалла цилиндрического сечения

S kin = 2 na h R ² J 1 ( q о R ) /q о ,          (4)

где J 1 ( q о R ) — функция Бесселя первого порядка.

3.    Численное моделирование

Численное моделирование динамической дифракции выполнено для кристаллов кремния цилиндрического сечения разного радиуса от 3 до 50 µ m с применением рекуррентной процедуры (1) и (2). Для вычисления карт RSM в кинематическом приближении использованы решение (4) и двумерные рекуррентные соотношения (1) с учетом r = 0 и r о = 0 . Результаты вычислений этими двумя методами совпадают.

Использованы табличные данные для симметричного отражения σ -поляризованного рентгеновского CuK α ₁ — излучения с длиной волны X = 1 , 54 А [11]. Длина первичной экстинкции в геометрии Брэгга есть l _ext = 1 , 51 цт , период маятниковых осцилляций в геометрии Лауэ l _pen = 18 , 7 цт . Угол Брэгга для симметричного отражения равен 14,221 угл. град., межплоскостное расстояние d 111 = 3 , 1355 А.

4.    Рентгеновские волновые поля внутри цилиндрического кристалла

Ранее с использованием двумерных рекуррентных соотношений была исследована динамическая Брэгг-Лауэ дифракция на латеральном кристалле прямоугольного сечения [7]. Показано, что в таком кристалле одновременно выполняются дифракция Брэгга и дифракция Лауэ. Для кристалла, у которого толщина превышает его ширину, реализуется случай Брэгга. Если ширина кристалла существенно превышает его толщину, имеет место случай Лауэ.

Используя двумерные рекуррентные соотношения (1), вычислим распределение интенсивностей рентгеновских полей внутри цилиндрического кристалла при выполнении точного условия Брэгга для отражающих решеточных плоскостей. Рентгеновские поля представлены в линейном масштабе, отношение между соседними линиями интенсивностей равно 0,1. Максимальное значение интенсивности соответствует красному цвету, минимальное значение имеет фиолетовый цвет.

В случае малого радиуса цилиндрического сечения ( R = 3 ц m и R = 7 , 5 цт ) распределение интенсивностей показано на рис. 2. Для кристалла радиуса R = 3 цт интенсивность проходящей волны медленно уменьшается (рис. 2 b), а интенсивность дифрагированной волны постепенно увеличивается (рис. 2 a). Такое распределение волновых полей примерно соответствует кинематическому приближению (в строгой интерпретации кинематическая дифракция предполагает неизменную в пространстве или уменьшающуюся только из-за поглощения интенсивность проходящей волны). Поэтому мы не показываем распределение интенсивностей рентгеновских полей внутри цилиндрического кристалла в случае кинематической дифракции.

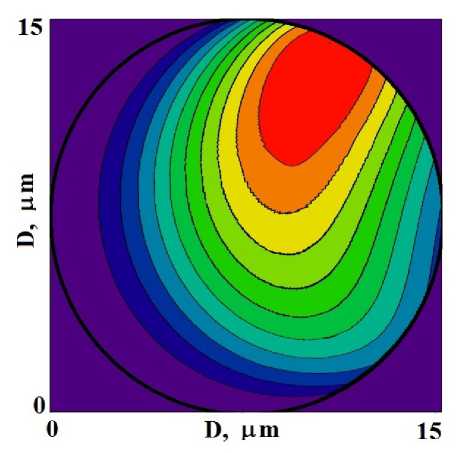
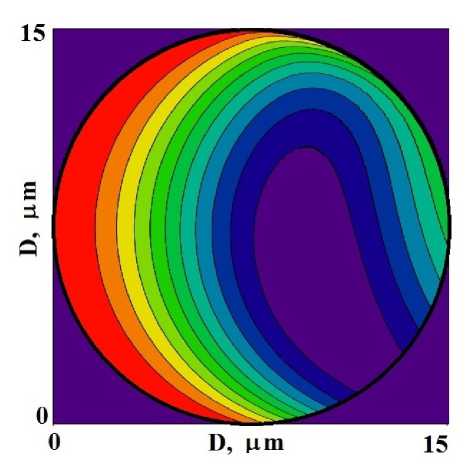
Для цилиндрического кристалла радиуса R = 7 , 5 цт распределение интенсивностей волновых полей показано на рис. 2 c, d. Пятно максимальной дифрагированной интенсивности сместилось вверх (рис. 2 c). В распределении проходящего волнового поля возникает область малой интенсивности из-за первичной экстинкции (рис. 2 d). Таким образом, в случае цилиндрических кристаллов малого радиуса сечения преимущественно реализуется дифракция Брэгга.

Распределение интенсивностей в объеме кристаллов с большими радиусами поперечных сечений показано на рис. 3. Для таких кристаллов выполняется условие Брэг-га-Лауэ дифракции. Кроме дифракции Брэгга, в верхней части кристаллов наблюдается маятниковый эффект Лауэ дифракции (рис. 3).

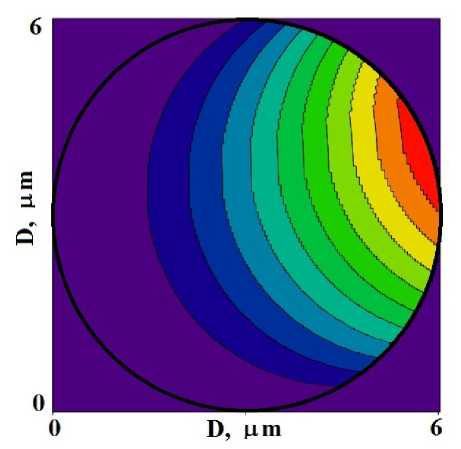
(a)

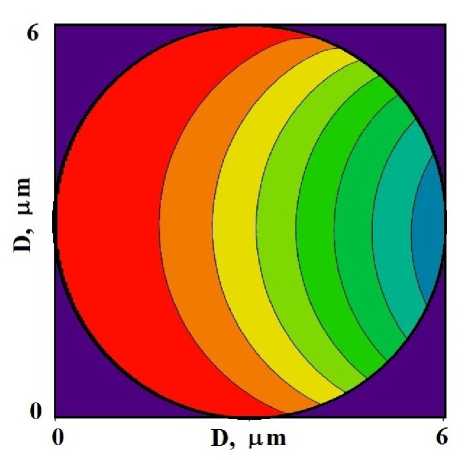
(b)

(c)

(d)

Рисунок 2. Распределение интенсивностей дифракционных (a, c) и проходящих (b, d) рентгеновских полей внутри цилиндрических кристаллов малых радиусов (диаметров D = 2 R ) поперечного сечения: (a, b) — R = 3 цт , (c, d) — R = 7 , 5 цт .

Figure 2. Intensity distribution of diffraction (a, c) and transmitted (b, d) X-ray fields inside cylindrical crystals of small radii (diameters D = 2 R ) of cross section: (a, b) — R = 3 цт , (c, d) — R = 7 . 5 цт .

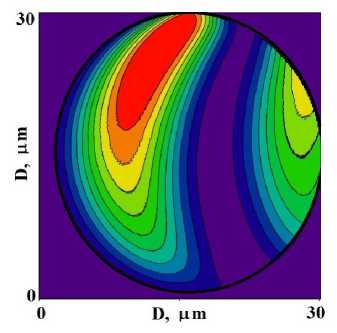
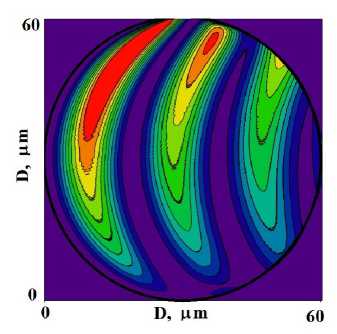
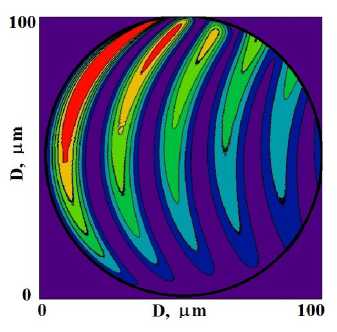
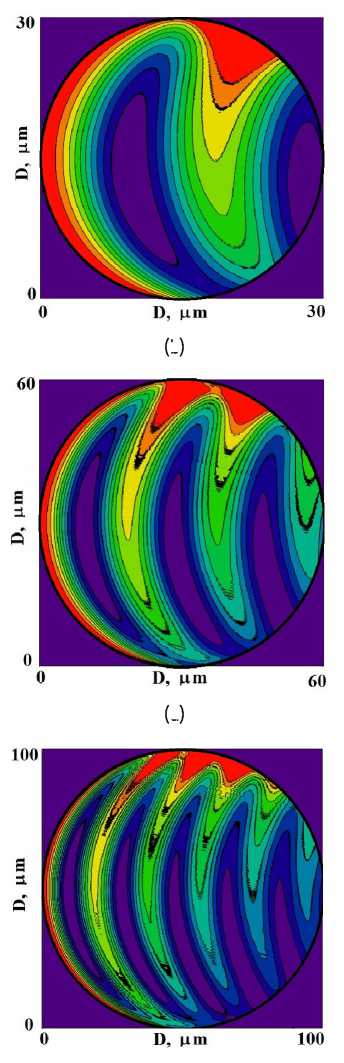
В цилиндрических кристаллах радиуса R = 15 цт в направлении Лауэ дифракции укладывается более полутора периодов маятниковых осцилляций. Поэтому формируются две области дифракции, между которыми имеется провал малой интенсивности (рис. 3 a). В распределении проходящего пучка на месте этого провала формируется область с максимальной интенсивностью (рис. 3 b). По диаметру кристалла с R = 30 цт укладывается три периода маятниковых осцилляций (рис. 3 c, d) , а кристалла с R = 50 цт таких периодов более пяти (рис. 3 e, f).

Заключение

Таким образом, мы впервые вычислили распределения рентгеновских интенсивностей дифракционного и прохо- дящего пучков в объеме совершенного цилиндрического кристалла и карты RSM. Это будет полезным для анализа экспериментальных результатов. Рассмотренный подход позволяет изучать динамическую дифракцию на кристаллах произвольной формы. В частности, для (Mx Ах/2) p + (Nzd/2)p = Rp, где p ~ 100, имеет место дифракция на кристалле квадратного сечения, а в случае (Mx Ах/2)2/R 2 + (Nzd/2)2/R 2 = 1 — дифракция на кристалле эллиптического сечения, где R1,2 — эллиптические оси. Кроме того, с использованием двумерных рекуррентных соотношений можно исследовать проблемы первичной экстинкции и поглощения в цилиндрических кристаллах, а также решать задачи дифракции в таких кристаллах с деформациями и дефектами.

(a)

(c)

(e)

(b)

(d)

(f)

Рисунок 3. Распределение интенсивностей дифракционных (a, c) и проходящих (b, d) рентгеновских полей внутри цилиндрических кристаллов больших радиусов (диаметров D = 2 R ) поперечного сечения: (a, b) — R = 15 µm , (c, d) — R = 30 µm , (e, f) — R = 50 µm .

Figure 3. Intensity distribution of diffractive (a, c) and transmitted (b, d) X-ray fields inside cylindrical crystals of large radii (diameters D = 2 R ) of cross section: (a, b) — R = 15 µm , (c, d) — R = 30 µm , (e, f) — R = 50 µm .