Дифракция рентгеновских лучей в кристалле трапецеидального сечения

Достижения методов литографии и селективного эпитаксиального роста кристаллов позволяют создавать разнообразные по форме латерально ограниченные структуры. Такие кристаллические системы используются для сверхбыстрых транзисторов, полупроводниковых лазеров и детекторов. Известно, что в планарных кристаллических слоях возникают упругие деформации в стыкующихся материалах, которые часто сопровождаются генерацией дислокаций, изгибом пластин и трещинами. Совсем недавно появились новые уникальные возможно- сти создания латеральных структур. В работах [1,2] предложено устранить эти недостатки быстрой, низкотемпературной эпитаксией кристаллов германия и SiGe с использованием микронных по высоте колонн, выгравированных на Si (001) подложках. Такой метод 3D гетероэпитаксии позволяет заменить непрерывные пленки латерально ограниченными бездефектными кристаллами микронных размеров.

Как и в случае планарных систем, структурное совершенство 3D кристаллов может быть исследовано методом высокоразрешающей рентгеновской дифракции. Таким образом, в настоящее время становятся весьма актуальными расчеты рентгенов- ской дифракции от латерально ограниченных кристаллических структур. В кинематическом приближении теории дифракции в кристаллах трапецеидального сечения со структурными дефектами и упругими деформациями разработаны в [3–6]. В работе [7] предложен алгоритм расчета дифракции рентгеновских лучей от многослойных латеральных кристаллических структур произвольного композиционного состава и формы.

В силу того, что 3D-кристаллы могут иметь микронные размеры, как правило, превышающие длину первичной экстинкции, то возникают сомнения о правомочности применения кинематического приближения. На основе уравнений Такаги разработаны методы расчета динамической дифракции от кристалла прямоугольного сечения [8]. Показано, что для узкого кристалла толщиной, существенно превышающей длину экстинкции, кривые дифракционного отражения (КДО), рассчитанные по формулам динамической дифракции, практически совпадают с КДО кинематического приближения. Позже для описания динамической рентгеновской дифракции в ла-терально ограниченном кристалле разработан подход, базирующийся на рекуррентных соотношениях [9,10]. В отличие от хорошо известных одномерных рекуррентных формул Дарвина [11], новые рекуррентные соотношения [9,10] относятся к задачам двумерной рентгеновской дифракции и позволяют рассчитывать карты распределения интенсивности рассеяния вблизи узла обратной решетки.

Цель данной работы — рассмотрение динамической дифракции рентгеновских лучей в кристалле трапецеидального сечения на основе рекуррентных соотношений [9,10], а также в сравнении полученных результатов с кинематическим приближением [3–6].

Динамическая дифракция в кристалле трапецеидального сечения

Сначала сделаем несколько предварительных замечаний. Пусть d — межплоскостное расстояние отражающих атомных плоскостей, для которых выполняется известный закон 2 d sin 9 b = А , где 9B — угол Брэгга, λ — длина волны падающего рентгеновского излучения. В работе [9,10] для описания дифракции на кристалле прямоугольного сечения использована модель Дарвина [11] с коэффициентами отражения и пропускания одной атомной плоскостью, бесконечной в латеральном направлении, поэтому такая модель для латерально ограниченных структур в какой-то степени является приближенной.

Дифракция рентгеновских лучей в континуальной среде зависит от Фурье-коэффициентов поляризуемости X g = -г о А ² F g / ( nV c ) , где F g — структурный фактор, λ — длина волны падающего излучения, V c — объем элементарной ячейки, r ₀ = e ² / ( mc ²) — классический радиус электрона, e , m — заряд и масса электрона. Динамические коэффициенты a ₀ ,h = пх ₀ ,h / ( А sin 9 b ) в уравнениях Такаги характеризуют взаимодействие рентгеновских полей в латераль-но бесконечном кристалле единичной толщины, при этом амплитуды пропускания (рассеяния вперед) r ₀ и отражения r _h от одной атомной плоскости в мо-

дели Дарвина связаны с этими коэффициентами как r ₀ ,h = a ₀ ,h d . Это означает, что в модели Дарвина вся электронная плотность континуальной среды, заключенная между соседними атомными плоскостями, сосредоточена в бесконечно тонкой атомной плоскости.

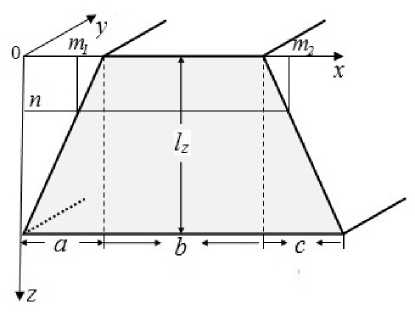
Рис. 1. Схематическое изображение кристалла трапецеидального сечения.

Fig. 1 Schematic representation of a trapezoidal cross-section crystal.

Рассмотрим для простоты симметричную дифракцию σ -поляризованного излучения на совершенном кристалле трапецеидального сечения (КТС) толщиной l _z , верхним основанием b , нижним основанием a + b + c (рис. 1). При определенных изменениях параметров трапеция трансформируется в сечение прямоугольной ( a = c = 0 ) или треугольной ( b = 0 ) формы, а также в сечение в виде параллелограмма ( a = —c ). Пусть N z — число атомных плоскостей в кристалле, вдоль a укладывается m _a разбиений A x , вдоль b — m b и вдоль c — m c таких разбиений. Полное число разбиений вдоль оси x равно M _x = m a + m b + m c .Пусть T ™ — значение амплитуды проходящей волны непосредственно перед узлом ( m ; n ), S m — соответствующее значение амплитуды отраженной волны. С учетом динамического рассеяния для отраженных S и проходящих T волн можно записать следующие рекуррентные соотношения [9]:

m

T n +1

= -i ¹

+ rS

m

п

,

1 m   ^ c m — 1 । m m — 1 'n = t S n +1 ⁺ r T n +1 ,

где t = t = (1 + r о ) exp( iф d ) , r = r _K exp( iф d ) , r_ = r h exp( iф d ) , r g м —iX g nd/ ( А sin 9 b ) ( g = 0 , h, h ) , ф _d = i 2 nd/ ( А sin 9 _b ) .

Рекуррентные соотношения (1) определяют структуру динамического взаимодействия проходящих и отраженных рентгеновских волн. Для описания дифракции в кристалле заданной формы необходимо исходить из граничных условий.

Пусть на кристалл падает рентгеновский пучок под углом 9 1 = 9 _b + A 9 1 к отражающим атомным плоскостям. При прохождении рентгеновских лучей, как в вакууме, так и в объеме кристалла происходит изменение фаз рентгеновских волн. За начало отсчета фазовых изменений выберем начало системы координат ( x = 0; z = 0 , рис. 1.). В этой точке амплитуда падающей волны T 0 равна единице. Для рент-

геновских волн, фронт которых ограничен вертикальной осью z , разность хода растет с ростом n по закону nd sin 9 1 , а разность фаз вдоль вертикального направления изменяется как фП_т = (2 п/Х ) nd sin 9 1 . Поэтому граничное условие сверху вниз вдоль оси z имеет вид T ⁰ = exp( iф n,_in ) , где n = 0 , 1 , 2 ,..., N z . Для верхнего фронта рентгеновских волн, начинающегося от начала координат и распространяющегося вдоль оси x , разность хода растет с ростом номера узла m как m A x cos 9 1 , а разность фаз вдоль горизонтального направления изменяется по закону ф О⁰™ = (2 п/Х ) m A x cos 9 1 . Граничное условие на этом участке задается выражением Т О = exp( iф mi_n ) , где m = 0 , 1 , 2 ,..., M x . При выше заданных граничных условиях распространение рентгеновских волн как в вакууме, так и в объеме кристалла может быть описано уравнениями (1) с учетом того, что в вакууме r g = 0 . Поэтапно реализуя процедуру рекуррентных вычислений, изложенную в работе [9], необходимо ввести ограничения, связанные с границами раздела вакуум-кристалл. Так, например, рентгеновская волна, распространялась в вакууме до узла ( n, m 1 ), имеет фазовые изменения, при этом амплитуды отраженных рентгеновских волн от атомных плоскостей как вперед, так и в направлении дифракции равны нулю (рис. 1). При этом вычисления производятся с использованием формулы Т 0 ₊₁ = T m- ¹ exp( iф _d ) . Как только эта волна достигает границы кристалла, то с ростом n и m начинает полноценно «работать» рекуррентная процедура (1). Это продолжается до тех пор, пока, например, не будет достигнут узел ( n, m ₂ ), после чего в соотношениях (1) необходимо снова принять условие r g = 0 (рис. 1). Таким образом, вычисления проводятся по всем узлам прямоугольной решетки M _x х N z с использованием границ раздела вакуум-кристалл. Подробный алгоритм вычислений изложен в работе [9].

В рассматриваемом случае кристалла трапецеидального сечения граничная задача сводится к следующей процедуре: если для всех m = 0, 1, 2,..., Mx выполняется условие ma n

N z ctg « B n 6 m 6 m + m b + m (1 - n-^ ) , тогда вычисления реализуются по рекуррентной процедуре (1), в противном случае в этих соотношениях следует принять r _g = 0 .

Для фиксированного угла падения рентгеновского пучка на кристалл под углом 91 в трехосевой дифракционной схеме регистрируются выходящие (дифракционные и проходящие) пучки под разными углами, например, 92. В этом случае возникают дополнительные фазовые изменения рентгеновских волн в вертикальной фП S = (2 п/Х)[ nd sin 9 2 — Mx Ax cos 9 2] и горизонтальной Фm,S = — (2п/Х)mAx cos 92 плоскостях для отраженной волны S. Процедура расчетов должна быть дополнена граничными условиями для выходящих из кристалла рентгеновских волн: Sn = 0, Smz = 0. Интенсивность отражения рентгеновской волны на- ходится из соотношения

I h ⁽ q x ,q z )     | ^{S (} q x ,q z ) |

। Mx                         ^Nz                      12

= | V S₀ m exp( iф ms ) + £ S Mx exp( iф ns ) | , m =0                 n =1

где амплитуды дифракционных рентгеновских волн S _n ⁰ и S _n ^{M x} вычисляются с помощью рекуррентных соотношений (1).

Кинематическая дифракция в кристалле трапецеидального сечения

В кинематическом приближении в уравнениях (1) следует принять r = 0 и t = exp( iф _d ) , поскольку отсутствует процесс многократного рассеяния рентгеновских лучей из проходящей волны в дифракционный пучок и обратно (отсутствует первичная экстинкция) и интенсивность проходящего пучка остается неизменной. Здесь следует учесть весьма важное обстоятельство, связанное с тем, что в «кинематических» рекуррентных соотношениях учитываются преломление и поглощение проходящего рентгеновского пучка. В общепринятом понимании кинематического приближения эффектами поглощения и преломления, как правило, пренебрегают.

Амплитуда отраженной рентгеновской волны от трапецеидального кристалла в кинематическом приближении вблизи узла обратной решетки без учета поглощения и преломления проходящего рентгеновского пучка запишется в виде

/• lz             r^X z )

E h ( q x ,q z )= ia h J dze iqzz J       dxe^ xx . (3)

Пределы интегрирования в (3) для трапеции с верхним основанием b , нижним основанием a + b + c и высотой l _z (рис. 1) для произвольной координаты z запишутся как: Q 1 ( z ) = ( l z —z ) a и Q ₂ ( z ) = a + b + ic z . Последовательно вычисляя интегралы в выражении (3), получаем аналитическое решение для амплитуды рентгеновского отражения от кристалла трапецеидального сечения в кинематическом приближении [5]:

TZ ₍ A     r h N z Г iq. a+c+ + b) ■     ⁽ q z l z ⁺ q x c ) .

Eh(qx,qz) =e qx( 2 + ) sinc+ qx2

, .    (qzlz — qxc\\

+ =,nc(----2Л где sinc x = sin x/x, толщина кристалла представлена как lz = Nzd и rh = ahd. Интенсивность рассеяния рентгеновских лучей может быть вычислена по стандартной формуле

I h ^{( q} x ^,q z ) ^{| E} h ⁽ q x , q z ) | * ⁽⁵⁾

Численное моделирование. Сравнение динамической и кинематической дифракции

Численное моделирование рентгеновской дифракции в кристалле кремния с трапецеидальным сечением выполнено для (111) отражения σ-поляри-зованного CuKα излучения. Толщина кристалла во всех расчетах составляла 3 µm, которая в два раза превышала длину первичной экстинкции (lext = 1,5 µm). Вычисления динамической дифракции проводились с использованием решения (2), кинематического приближения по формулам (4) и (5).

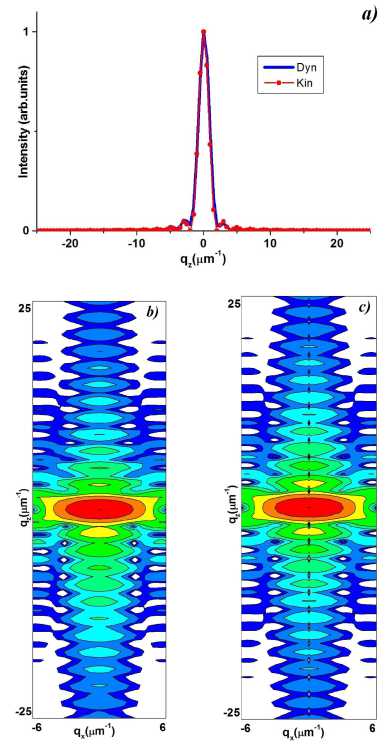
Рис. 2. Расчетные q z -сечения (a) и RSM динамической (b) и кинематической (c) дифракции от КТС. l _z = 3 µm ; a = b = c = 0 , 5 µm .

Fig. 2. Calculated q z -section (a) and RSM of dynamical (b) and kinematical (c) diffraction from a trapezoidal cross-section crystal. l _z = 3 µm ; a = b = c = 0 , 5 µm .

На рис.2 приведены результаты динамической и кинематической дифракции в «узком» КТС ( a = b = c = 0 , 5 µm ), нижнее основание которого в два раза меньше толщины кристалла. Нетрудно видеть, что как кривые дифракционного отражения (КДО, рис. 2a), так и карты распределения интенсивности рассеяния в обратном пространстве (reciprocal space map (RSM)) динамической (рис. 2b) и кинематической (рис. 2c) дифракции практически совпадают. Здесь и на последующих картах контуры равной интенсивности представлены в логарифмическом масштабе, отношение интенсивностей соседних линий равно 0,273. Таким образом, для «узкого», хотя и толстого КТС, справедливо кинематическое приближение.

В последующих вычислениях кристаллы трапецеидального сечения также имели толщину 3 µm , а отрезки нижнего основания трапеции составляли a = c = 3 µm . В численном моделировании изменялась длина верхнего основания трапеции b , при этом углы наклона сторон трапеции к нижнему основанию составляли α = β = 45 угл. градуса (рис. 1).

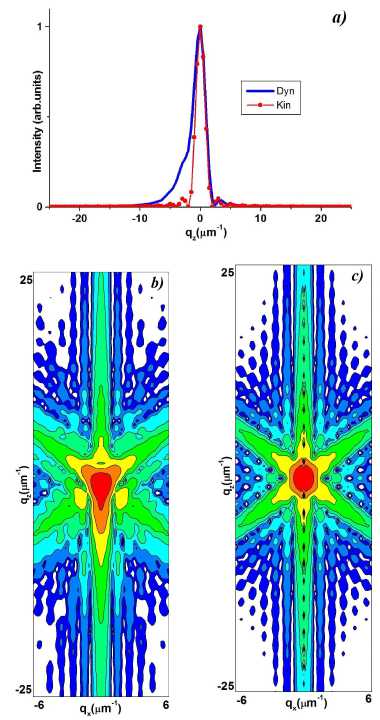
Рис. 3. Расчетные q _z -сечения (a) и RSM динамической (b) и кинематической (c) дифракции от КТС. lz = 3 µm ; a = c = 3 µm ; b = 0 µm .

Fig. 3. Calculated q z -section (a) and RSM of dynamical (b) and kinematical (c) diffraction from a trapezoidal cross-section crystal. l _z = 3 µm ; a = c = 3 µm ; b = 0 µm .

Рис. 3 демонстрирует КДО ( q _z -сечения) и RSM от кристалла треугольного сечения (верхнее основание b = 0 ) с нижним основанием 6 µm . В данном случае уже имеются отличия в расчетах динамической и кинематической дифракции. На профиле КДО, рассчитанным с использованием решения (2), появился «наплыв», характерный переходу от кинематического приближения к динамической дифракции (рис. 3a). Отличаются также динамическая и кинематическая карты RSM (рис. 3b,c). Направление наклонных полос на картах связано с углом наклона сторон КТС относительно нижнего основания трапеции. Отметим, что в отличие от динамической дифракционной картины распределение интенсивности на RSM в кинематическом случае имеет симметричный вид вдоль вертикального направления.

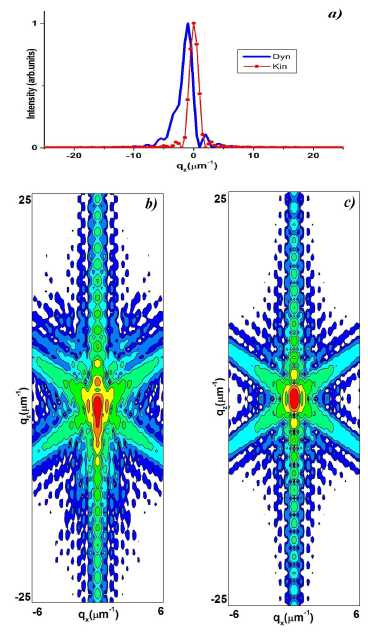
Рис. 4. Расчетные q _z -сечения (a) и RSM динамической (b) и кинематической (c) дифракции от КТС. lz = 3 цт ; a = c = 3 цт ; b = 6 цт .

Fig. 4. Calculated q z -section (a) and RSM of dynamical (b) and kinematical (c) diffraction from a trapezoidal cross-section crystal. l z = 3 цт ; a = c = 3 цт ; b = 6 цт .

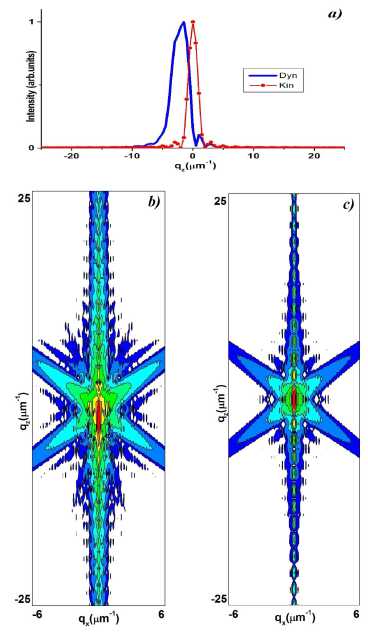
Рис. 5. Расчетные q _z -сечения (a) и RSM динамической (b) и кинематической (c) дифракции от КТС. lz = 3 цт ; a = c = 3 цт ; b = 25 цт .

Fig. 5. Calculated q z -section (a) and RSM of dynamical (b) and kinematical (c) diffraction from a trapezoidal cross-section crystal. lz = 3 цт ; a = c = 3 цт ; b = 25 цт

На рис. 4 показаны результаты численного моделирования рентгеновской дифракции от КТС с верхним основанием b = 6 цт , соответственно нижнее основание трапеции составляет 12 цт . Из-за преломления рентгеновских лучей КДО динамического рассеяния сдвигается влево, при этом «наплыв» интенсивности увеличивается.

В случае широкого кристалла ( b = 25 цт ) профиль КДО, рассчитанный по рекуррентным соотношениям, уже имеет контуры дарвиновской кривой отражения (рис. 5а). Динамическая карта RSM характеризуется не только сдвигом максимума интенсивности вдоль q z направления, но и из-за первичной экстинкции, т. е. более сильного взаимодействия рентгеновских квантов со средой, становится и более широкой в вертикальном направлении (рис. 5b,c).

Заключение

Принципиальной особенностью разработанного подхода является возможность расчетов кривых дифракционного отражения и карт RSM от латеральных кристаллов с трапецеидальным сечением в рамках более общей динамической дифракции. Следует также подчеркнуть, что изложенный в работе метод позволяет рассматривать динамическую дифракцию рентгеновских лучей от кристаллов с произвольной формой поперечного сечения. Это является весьма важным аспектом, поскольку в современных технологических условиях методами литографии и селективного роста создаются рельефные структуры различного вида. Следующим шагом будет развитие теории динамической дифракции в латерально ограниченных кристаллах с упругими деформациями кристаллической решетки, а также с учетом статистически распределенных структурных дефектов. Изложенный метод рекуррентных соотношений будет весьма полезен не только в задачах рентгеновской или нейтронной оптики, но и в оптике фотонных и жидких кристаллов.

Работа выполнена при частичной финансовой поддержке Программы фундаментальных исследований УрО РАН (проект 15-9-1-13) и РФФИ (проекты №17-02-00090 и № 16-43-110350).