Дифракция света на прямоугольном отверстии со статистически неровной границей

При изготовлении и эксплуатации прецизионных оптикоэлектронных и электронно-оптических датчиков перемещений необходимо корректно оценивать нелинейность функции отклика и систематическую приборную погрешность измерений, возникающую из-за дифракции и несовершенства технологии изготовления датчиков [5, 7, 8, 9, 10].

Целью настоящей работы является оценка совместного влияния этих факторов на интенсивность регистрируемого сигнала в случае, когда диафрагма фотоприемника имеет прямоугольную форму.

Для этого рассмотрим задачу о дифракции плоской волны на отверстии, имеющем форму, близкую к прямоугольной. Это означает, что если прямоугольное отверстие имеет ширину a и высоту b , то для квазипрямоугольного отверстия со статистически неровной границей выполняются соотношения:

где U – амплитуда падающей волны в окрестности отверстия, k – модуль волнового вектора падающей волны, df – площадь участка волновой поверхности, df_n – проекция вектора df на плоскость, перпендикулярную направлению падающего луча све-та¹, а абсолютная величина радиус-вектора R в формуле (2) выражается через координаты ( X , Y , Z ) точки наблюдения P и координаты точек волновой поверхности ( x , y , z ):

R = V ( X - x ) 2 + ( Y - У ) 2 + ( Z - z ) 2 .             (3)

Соотношения (2)-(3) являются основой для формальной постановки последующих задач.

Дифракция на прямоугольном отверстии

Пусть световая волна падает по нормали на идеальное прямоугольное отверстие в плоском экране, лежащем в плоскости xy . Если отверстие имеет

8 a .

— ^ 1 a

8 b , b * 1,

где 8 a = 8 a ( y ) и 8 b = 8 b ( x ) - случайные функции.

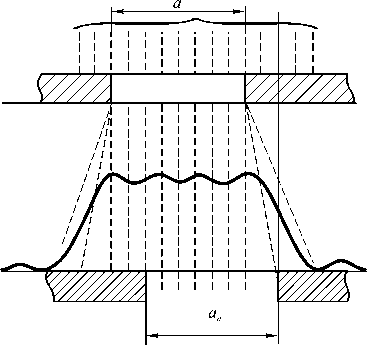
Рис. 1. Схема регистрации дифрагированного света

В случае дифракции плоской волны на отверстии произвольной формы амплитуда дифрагированной волны U_p в точке наблюдения P равна [1]:

ширину a и высоту b , то координаты точек волновой поверхности удовлетворяют условиям:

f- a /2 <  x <  a /2,

J- b /2 <  y <  b /2,                             (4)

I z = 0,

В этом случае амплитуда U падающей волны в формуле (2) одинакова для всех точек волновой поверхности, лежащей в плоскости экрана ( U = U ₀ = const ), соотношение (2) приобретает вид:

U p

ab kU0 22

—- ■ J dx J dy ■ 2n i -1   _b

2      2

e ikJ ( X - x )² + ( Y - y )² + Z ²

V( X - x ) ² + ( Y - y ) ² + Z^{2 ,}

и амплитуда дифрагированной волны вычисляется элементарно2:

Up=J

kU

2n iR

eikR

■ f ,

¹ Вектор df направлен вдоль внешней нормали к волновой поверхности.

2 Обозначения и определения см. в приложении.

ikZ

U p ( X , Y , Z ) * ^- ■    "

2 i

отверстием. Поэтому k x ² + k y = k ² sin ² 9 , и при 9 « 1

выполняется соотношение:

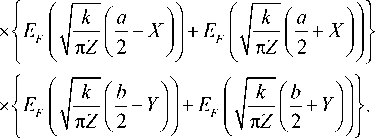
1     ,          9 ²

1—sin ² 9 * 1 * cos 9 .

Следовательно, для случая малых углов падения световой волны на экран ( 9 « 1) с учетом соотношения (13) и того, что k z / k = cos 9 , получаем:

При переходе от соотношения (5) к выражению (6) мы использовали стандартное разложение величины R по малому параметру теории дифракции:

V( X - x ) ² + ( Y - y ) ² + Z² *

1( X - x ) ² + ( Y - y ) ^{2                      (7)}

* Z +                      .

2 Z

( k_x ² + k 22 ) Z —— kX + k Y + kZ - — y— * kR . xy     _{2 k}

Таким образом, в приближении малых углов падения световой волны ( 9 « 1) амплитуда дифраги-

В случае наклонного падения волны амплитуда U = U ( x , y ) зависит от координат точек волновой поверхности, и ее нельзя выносить из-под знака интеграла. В частности, если на отверстии в экране дифрагирует плоская волна, то

рованной волны имеет вид:

Up (X, Y, Z) = -0 ■ exp L i (k— ■ R )]x x LEf (JX+ ) + Ef (JX- )] LEf (Y+ ) + Ef (Y- )].

—*

U = U ₀ ■ exp( ikr ),

амплитуда световой волны в точке наблюдения P имеет вид:

^Up *

kU ₀ ■ e^lM 2 n iZ

Из (15) следует, что интенсивность света в точке наблюдения P равна:

I p ( X , Y , Z ) = U p ( X , Y , Z )|² =

2      ₂₂ (16)

= -4"-| E f ( X + ) + E f ( X -)| -| E f ( Y + ) + E f (Y - )| .

Выражения (15) и (16) описывают дифракцию плоской световой волны на прямоугольном отверстии.

a

2 LL.

xj dx ■ exp< i k x + k ■ a IL

( X - x ) ²

2 Z

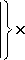
b

2 f x J dy ■ exp< i k y + k

^J b     ч L

( Y - y ) ²

2 Z

Дифракция на отверстии со статистически неровной границей

Рассмотрим случай дифракции на прямоугольном отверстии со статистически неровной границей. Для этого представим выражение для амплитуды U _p световой волны, дифрагированной на идеальном

и выражается через интегралы Френеля:

прямоугольном отверстии в непрозрачном экране в следующем виде:

U p o ( X , Y , Z ) =

Г                 ( k x + k 2 ) Z )

tt    i I k x X + k_yY + kZ y — I

U p ( X , Y , Z ) = -° ■ e ^{1             2 k  J} x

2 i

”

k_z Г j aI ^а IaI ^a I —— ■ dx 9 — x 9 x + — ■ 2 n i ^J 1 2    ||    2 J

-да

x L E f (J X +) + E f (J X -) ] ■ L E f (Y + ) + E f (Y - ) ] ,

” ²    lbb bb b I

■ U ( x , y , z ) ■ f dy 9| -- y |9| y + - ]■

-да X        z X        /

где

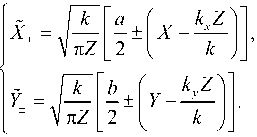
e ik 4 ( X - x )² + ( Y - y )² + Z ²

4 ( X - x ) ² + ( Y - y ) ² + Z ² "

Наблюдаемая амплитуда содержит вклад от дифракции на рельефе границы кодирующего элемента:

В сферической системы координат

kx = k sin 9 cos ф, < ky = k sin 9 sin ф, kz = k cos 9,

U p ( X , Y , Z ) = A J dx L y ■ u ( x , y , 0) ■ ^{2 n i      J}„

■9^ 2 + 8 _ra ( y ) - x J ■ 9^ x + 2 + 8 l a ( y ) J ■

■⁹f 2 ^{+ 8} u ^{b ( x} ) ^- у l⁹f у ⁺ 2 ^{+ 8} d ^{b ( x} ) ¹ ■

где 9 - угол между направлением луча и плоскостью – xy , в которой лежит экран с прямоугольным

_e ik j ( X - x )² + ( Y - y )² + Z²

.

V( X - x )² + ( Y - y )² + Z²

Для вычисления амплитуды (18) воспользуемся свойствами обобщенных функций:

e^f a + 5 l - x 1«ef a - x 1 + 5^f a - x Is l ,       (19)

12 JI 2 J J 2 J где l = a, b, 51 = 5ar, 5al, 5bu, 5bd .

Подставляя (19) в (18) и пренебрегая поправками второго порядка, получаем:

5 U p ( X , Y , Z ) = ^ 5 U,. ,                        (20)

i = 1

Где явное выражение для каждой парциальной амплитуды 5 U i будет приведено ниже.

Воспользуемся основной идеей теории дифракции (см. формулу (7), и представим первое слагаемое в разложении (20) в следующем виде:

(5 a ( k , k x , X )) =

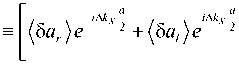
x e

- • • "    ² 1

Тогда из формул (24)-(26) вытекает, что

(5 U 1) + (5 U ₂) «(5 a ( k , k x , X )}х

^^U ^E F ^{( Y} + ) ^{+ E} F ^{( Y} - ’ ] -

Для второй пары границ отверстия аналогичным образом получаем:

(5 U 3) + (5 U _; «(5 b ( k , ky , Y )) x

ПГ U                        (28)

xj —       '.. ■[ E f ( X + ) + E f (J X - ) ] ,

V nZ       2 i L                   J ikZ          a ke     ikx

5 U. =-- Ue ² ■

¹    2 п i Z ⁰

где

e

г          ,п b ц, [(X - a/2) 1 2                            (Y - У )2

^lk\ 2 Z I f             х ik y y + ik ⁽—~

; ^[ J dy 5 r a ( y ) e       ^{2 Z}

- b 2

(5 b ( k , k y , Y )) =

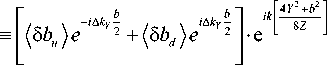
Для оценки априорной приборной погрешности, связанной с дифракцией на статистически неровной границе диафрагмы, необходимо провести усреднение по статистическому ансамблю датчиков. В соответствии с этим введем величину (S U i ^. В этом случае ^5 r a ( y )^ = const , и этот множитель можно вынести из под знака интеграла. В результате получаем:

к ⁵ «Н О^

^U 0 e i'kz 2 i

ik_ya + ik l x 2 I

e

( X - a I2)² 2 Z

X

x[ E f ( Y ) + E f ( Y - ) ] .

В рамках используемых приближений

k_x « kX , X_Z

Соотношения (26)-(29) дают полное решение задачи о нахождении амплитуды световой волны, дифрагированной на прямоугольном отверстии со статистически неровной границей.

Дифракция на узкой щели со статистически неровной границей

Рассмотрим узкую щель со статистически неровной границей. В этом случае поправкой (5 U ₃^ + ^5 U ₄) можно пренебречь, и выражение для полной амплитуды световой волны в точке наблюдения принимает вид:

U p ( X , Y , Z ) = U ⁰ ■ [ E_f ( i j ) + E f (Y - ) ]x

2i x{ei(kR )■ [ Ef (JX+) + Ef (JX-)]+                   (30)

+ e^iK^ (5 a ( k , k_x , X )7

поэтому целесообразно ввести величину

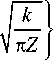
A k_X = k_X - k x . Тогда из (22) и (23) следует, что:

<^{5 u} 1>-<= — yjlZU

a, J4 X ² + a ^{2 1}

- i A k у —+ ik --------

X 2        8 Z |

■ e ^{L ]} x

Для оценки относительной априорной погрешности датчика перемещений необходимо рассчитать величину отношения 5 I P I I P .

Из соотношений (16) и (30) следует, что:

x[ E f ( Y ) + E f ( Y ) ] ,

и, аналогично,

IP

I

P 0

— —

e i ( k - R ) + e ikZ

(5 a ( k , k x , X )) ГД ' Ef (J X + ) + E f (J X - )" Ъ Z '

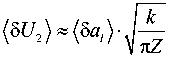
^U 0 e ikZ

2 i

x[ E f ( Y ) + E f ( Y_ ) ] .

+ i A k x —+ ik I

■ e 2 1

X

В рамках используемых приближений без ограничения общности можно ограничиться рассмотрением случая:

Введем характеристическую величину, описывающую флуктуации эффективной ширины щели для заданной длины падающей волны:

К 5 a ( k , k x , X )} |« 1.

Тогда, удерживая члены первого порядка малости по (5 a ), получаем:

8 I     , „| /Г" e i-kZ^{R )]} -(8 a ( k , k_x , X ))

2 Re

Ц      [b Z    E f ( X + ) + E f ( X - )

Соотношение (33) позволяет дать априорную оценку минимальной неустранимой приборной погрешности показаний датчика перемещений.

Функция отклика оптикоэлектронного датчика перемещений

Функция отклика оптического датчика h ( X_d ) по определению имеет вид:

h(Xd) — J ф(X, Y)Ip (X, Y, Z)dsn , (34) Sd где ф(X, Y) - аппаратная функция, а dsn - проекция элемента светочувствительной поверхности датчика на плоскость, нормальную к направлению падения светового луча.

В рамках настоящей работы предполагается, что ф ( X , Y ) — 1 на фотоэлементе датчика, и ф ( X , Y ) — 0 за его пределами. При этом a_d и b_d - ширина и высота входной диафрагмы фотоэлемента, соответственно, а X_d - величина смещения щели-осветителя относительно щели - диафрагмы фотоэлемента, т. е. искомое перемещение, измеряемое с помощью оптикоэлектронного датчика.

Для важного частного случая щелевидной диафрагмы фотоэлемента, входящего в состав датчика перемещений, заведомо выполняется условие b_d » a_d , и, следовательно, для интегралов Френеля можно использовать приближение E_F ( Y ) + E F ( Y - )| « 2. В этом приближении функция отклика выражается через полную энергию светового потока, падающего на входную диафрагму фотоэлемента h ( X d ) = W d ( X d ):

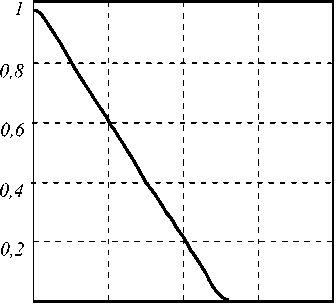
Рис. 2. Типичная функция отклика оптикоэлектронного датчика

S —     ; So — Д^;

n Z       V n Z 2

S₊—,f k - ^f X_d ± ad- ) ; A^— p-ZL .       (36)

± v n Z ( ^d 2J      \ n Z k

В данных обозначениях функция отклика принимает вид:

Wd (Xd) — W x s+                                                      (37)

x J E F ( S o + S - AS ) + E f ( S o - S - AS)| 2 d S ,

S- где Wo — Uo2bd       .

Для дальнейшего анализа удобно ввести безразмерную функцию отклика W_d ( X_d ), связанную с оптической функцией отклика W_d ( X_d ) очевидным соотношением:

-d (Xd) — Wo ■ Wd (Xd).(38)

Легко видеть, что W_d ( X_d ) выражается через вспомогательную функцию V ( S _o, n ):

Wd (Xd) — 4-V (So, 1+) - V (So, S-)],(39)

где S ± — S ± - AS , причем: п

V(So, п) — J EF (So + S) + Ef (So - S)|2 dS,(40)

^- n

Выражение (39) представим в следующем виде:

V (So, n) — Vo(So, n)-A V (So, n),(41)

где

Vo (So, n) — 2n ■ IEf (So + S) + Ef (So - S)|',(42)

и

п

AV(So,n) — 2 J F(So,S)SdS .(43)

-п

Подынтегральная функция F ( S _o, S ) в формуле (43) выражается через интегралы Френеля:

f ( S o , S ) — [ C ( S o +S ) + C ( S o -S ) ] x

П ^\2 П      _x2

^{x cos} 2 ^{( S} 0 ^{+S ) - cos}“^{( S} o ^{-S )}

+ [ s ( S o + S ) + 5 ( S o -S ) ] x

+

^sin |-^{( S} o ^{+S ) 2 - sin} |^{( S} 0 ^{-S ) 2}

U ²    X^d + a ^/2

W d ( X d ) —    b d  J

²     X d - ^a /2

|Ef ( X ₊ ) + E f ( X — )|² dX . (35)

Введем обозначения:

Несложно показать, что поправочная функция A V ( S _o, n ) может быть представлена в виде линейной комбинации интегралов специально вида:

A V (^, n) = — x a

x {B1 (a, в) - B1 (a, -в) - B2 (a, в) + B2 (a, -в)}, где a = —^2, в = —, а интегралы B, 2(a, в) опреде-2      ^

лены ниже:

B i ( a , в ) = j dt sin [ a t ( t - 2 + 2 в ) ] , 0

B ₂ ( a , в ) = [ — t sin [ a t ( t - 2 + 2 в ) ] .

Oo t

Интегралы B 1 ( a , в ) элементарно выражаются через интегралы Френеля:

B i ( a , в ) = "s^-^1)2] x

x[ S (^o(1 + в)) + 5 (^о(1 -в))]-                 (47)

- ^{sin[ a(}p^{- 1)2]} ^- C ( ^ о (1 + в ) ) + C ( ^ о (1 -в ) ) ] .

^ 0

Процедура вычисления интегралов B ₂( a , в ) существенно сложнее. Проблема состоит в том, что прямой расчет интегралов (46) по квадратурным формулам Симпсона, Гаусса и т.п. возможен далеко не при любых значениях параметров a и в . Эта проблема является общей проблемой нахождения численных квадратур от быстро осциллирующих функций. Она связана с быстрым накоплением погрешности при численном сложении большого числа знакопеременных слагаемых, имеющих один порядок величины.

В целях преодоления проблемы накопления погрешности вычислений представим интеграл B ₂( a , в ) виде суммы:

^B 2 ^{( a} , ^{в )} = A s ⁽ Р , q ) ⁺ A c ⁽ Р , q ),

где p = 4 a , q = 4 a ( в - 1), а вспомогательные функции A_s ( p , q ) и A_c ( p , q ) определены соотношениями (49) и (50).

A s ( Р , q ) ⁼ f dt sin( pt ²)cos( qt ),                 (49)

0t

A c ( p , q ) ^ j dt cos( pt ²)sin( qt ).                 (50)

0t

Таким образом, проблема нахождения функции отклика оптикоэлектронного датчика сводится к задаче вычисления интегралов специального вида A_s ( p , q ) и A_c ( p , q ). Рассмотрению этой проблемы посвящена отдельная работа [12].

Результаты расчетов

На рис. 3, 4 представлены результаты численных расчетов интенсивности I_P и суммарного сигнала

W_d ( X_d ) для случая падения зеленого света ( X = 0,55 мкм) на бесконечно длинную щель шириной а = 50 мкм при наличии зазора между кодирующей шкалой и фотоэлементом d = 50 мкм.

Из рисунков хорошо видно, что дифракционная картина носит ярко выраженный френелевский характер. Оптическая функция отклика W_d ( X_d ) нелинейна при малых X_d , что позволяет сделать вывод об актуальности рассматриваемой в статье задачи, поскольку наибольшие относительные погрешности датчиковая аппаратура выдает именно для малых значений угловых или линейных перемещений, наиболее интересных с прикладной точки зрения.

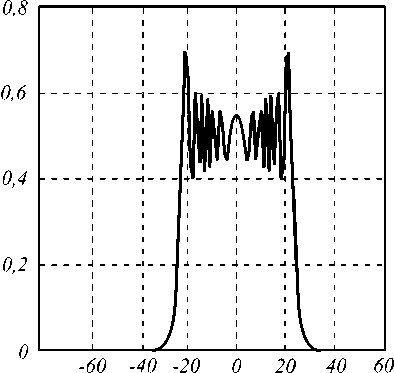
Рис.3. Амплитуда световой волны на поверхности фотоэлемента

Рис. 4. Реальная функция отклика оптикоэлектронного датчика

Заключение

Резюмируем вышесказанное следующим образом:

• 1.    Полученные выражения имеют прозрачный физический смысл. Вся информация о влиянии качества механической обработки границы окна кодирующей шкалы оптикоэлектронного датчика на уровень сигнала содержится в функциях (§ а ( k , k x , X )) и (5 b ( k , k y , Y )).

• 2.    Показано, что при анализе и синтезе оптикоэлектронных датчиков перемещений дифракция светового потока на кодирующей шкале является дифракцией Френеля.

• 3.    Построены вычислительно эффективные аналитические выражения для расчета интенсивности светового потока и интегрального сигнала W_d ( X_d ).

• 4.    Проведен численный анализ совместного влияния дифракционных и инструментальных погрешностей на работу оптикоэлектронных датчиков перемещений.

• 5.    Показано, что учет дифракционных явлений позволяет существенно улучшить точность датчиковой аппаратуры.

Представляется весьма перспективным использование разработанного формализма для решения задачи синтеза оптикоэлектронных датчиков перемещений с контролируемой нелинейностью оптической функции отклика.

Приложение

Определения и обозначения, используемые в работе

В работе используются стандартные определе- ния интегралов Френеля:

z x Г I П 2 It C (z) = I cos I — tI dt,

о V2 J

z x Г • I П 2 It S (z) = I sin I —t I dt,

0 ^{V 2 J}

(п1)

(п2)

быстрый алгоритм расчета которых построен в работах [3, 4, 6, 11].

Введем комплексный интеграл Френеля:

E F ( z ) = C ( z ) + iS ( z ) = zM

13 П 2 , , i z

22 2

(п3)

где M ( a , b , z ) – вырожденная гипергеометрическая функция.

Интегралы Френеля связаны со вспомогательными функциями f ( z ) и g ( z ) стандартными соот-

ношениями:
C ( z ) =	1 2 + f ( z )sin |	П z 2 ' . 2 j	|- g ( z )cos I	.i z 1 J •	(п4)
S ( z ) =	1 2 - f ( z )cos |	П z 2 " . 2 >	|- g ( z )sin [	П z 2 I . 2 1.	(п5)

Из соотношений (п1) –(п5) следует, что

Ef (z) = 1+i + [ f (z) - ig(z)] sin P| z2 |-

. I

• - [ g ( ^z ) ⁺ if ( ^z ) ] cos [у ^{z 2} J .

В асимптотике | z | » 1

nzf (z) =1 - —I??+-; nzg(z) = — ,

( n z )

и, следовательно,

• \ 1 + i i I ■ П 2 V/

Ef (z) «---exp I i — z I +....(п8)

2   nz[