Дифракция светового потока на чувствительных элементах волоконно-оптических и оптико-электронных датчиков механических перемещений

При создании волоконно-оптической и оптикоэлектронной датчиковой аппаратуры для измерения перемещений, положения, деформаций и других механических величин разработчикам всегда приходится учитывать особенности распространения светового потока через оптический тракт (ОТ) измерительного прибора.

При прохождении через ОТ излучение подвергается преобразованию в виде изменения интенсивности, фазы, направленности, поляризации или длины волны. Отраженный, пропущенный или переизлученный световой поток на выходе из ОТ поступает в фотоприемник, который выдает электрический сигнал, содержащий измерительную информацию.

К числу наиболее трудно устранимых источников погрешностей в оптическом тракте, ограничивающих точностные характеристики датчиков, относятся дифракционные явления [1,2]. В качестве примера влияния дифракции на форму и характер изменения несущего информацию сигнала рассмотрим упрощенную схему оптикоэлектронного датчи- ка линейных перемещений (рис.1), описанного в [2]. Параллельный световой поток от осветителя поступает на кодирующую шкалу 1, соединенную с объектом измерения. Кодирующая шкала (КШ) представляет собой оптически непрозрачную линейку (например, из металлической фольги) в которой вырезаны окна прозрачности. При линейном перемещении х КШ происходит амплитудная модуляция светового потока Ф(х), направляемого далее на неподвижный считывающий элемент (СчЭ) 2. В качестве источника излучения, как правило, используются лампы накаливания, электролюминесцентные диоды (светодиоды) или полупроводниковые лазеры, различающиеся между собой энергетическими, спектральными, фазовыми и пространственными характеристиками светового потока. Излучение, имеющее определенную диаграмму направленности, подводится к КШ волоконно-оптическими световодами или стандартными линзовыми оптическими системами. СчЭ воспринимает модулированный световой поток, который является носителем информации. Оптико-электронное преобразование осуществляется либо непосредственно в СчЭ, либо передается через оптическое волокно на изолированный фотоприемник (ФП). Код перемещения формируется путем реверсивного подсчета проходящих перед СчЭ окон КШ и аналого-цифрового преобразования сигнала с выхода ФП, соответствующего определенной доле периода нанесения окон КШ. При этом должны выдерживаться следующие геометрические соотношения между окнами КШ и СчЭ: a1 = a2 = a0/2, h1 > h2, d = 50...500 мкм, где a1, h1, a2, h2 -ширина и высота окон КШ и СчЭ соответственно, a0 - период КШ, d - расстояние от КШ до СчЭ (см. рис. 1). На рис. 2а пунктирной линией показаны эпюры сигнала с ФП, которые должны получиться при отсутствии инструментальных погрешностей, шумов излучателя и ФП, а также дифракции и рассеивания светового потока. Реальный сигнал, показанный сплошной линией, имеет ярко выраженные нелинейные участки в основаниях и вершинах “треугольников”. При аналогоцифровом преобразовании они создают ограничения по количеству достоверных разрядов кода перемещения n = log 2( Um(x)/A Umax(X)) - 1 (1) где Um(x) - амплитуда сигнала, а ∆Umax(x) - максимальное значение отклонения (погрешности) амплитуды сигнала

Рис. 2

Характер возникновения нелинейностей вследствие дифракции светового потока на доста- точно широкой прямоугольной щели, а также погрешности, возникающие за счет искажения формы щели, можно оценить, пользуясь математическим аппаратом, описанным в [5]. Целью настоящей работы является исследование влияния дифракции светового потока на КШ и СчЭ на амплитуду регистрируемого сигнала Um(x) с учетом инструментальных погрешностей и разработка способов расчета и компенсации возникающих при этом нелинейных искажений.

• 2.    ОСНОВНОЙ ФОРМАЛИЗМ

Во многих работах по оптикоэлектронным датчикам перемещений для расчета функции U m ( x ) ошибочно используется приближение дифракции Фраунгофера, в то время как реальные геометрические размеры окон датчиков соизмеримы с расстоянием от КШ до СчЭ и, следовательно, мы имеем дело с дифракцией Френеля. Дифракция Френеля имеет место несмотря на то, что падающую на КШ световую волну можно считать плоской; детально этот вопрос освещен в работе [5].

Пусть параллельный монохроматический пучок света падает на диафрагму под малым углом 9 к оси Z , перпендикулярной плоскости, в которой расположена КШ.

Используя обозначения и конвенции работы [5], представим комплексную амплитуду U p дифрагированной волны в точке наблюдения P в следующем виде:

U _ Г ku ⁽ x y, z ) e ikR df p " ^ 2n iR       ”

где k - волновой       вектор,

R _ J ( X — x )² + ( Y — y )² + ( Z — z )², X , Y , Z - координаты точки наблюдения P , U ( x , y , z ) - амплитуда световой волны на отверстии в экране (т.е. одном из отверстий в КШ), через который проходит световой поток, x , y , z - координаты точек волновой поверхности, по которой и производится интегрирование, а df n - проекция элемента площади волновой поверхности на плоскость, перпендикулярную направлению волнового вектора k [5]. Расчет амплитуды U p проведем в приближении Кирхгофа, в рамках которого малость угла дифракции приводит к тому, что в интеграл (2) существенный вклад дает только небольшая часть волновой поверхности, уравнение которой имеет вид z =0.

В этом случае

( X — x )² + ( Y — y )² + ( Z — z )² ® Z +

• + 1    _e ( x — x )² + ( y — y )^{2                      (3)}

2 Z

В первом приближении будем считать, что отверстия в КШ имеют прямоугольную форму. Тогда соответствующая интенсивность светового потока I p ( X , Y , Z ) выражается через стандартные интегралы Френеля C и S :

Ip (X,Y,Z)= u4 0 • cos² 9*

• • {[C(X+) + C(X-)]2 + [S(X +) + S(X-)]2} •

{[C(Y+) + C(Y- )]2 +[S(Y+) + S(Y- )]2} причем U0 -амплитуда световой волны на поверхности КШ, и, кроме того:

x ±=a      f a ± (x - kxZ)!

V n ■ Z L 2k

k kZ Y± = -----• b ± (Y - ^-) (6) V к-т L 2         k _ причем в формулах (5) и (6) предполагается, что a -ширина щели, а b - ее длина.

В случае неидеальной квазипрямоугольной щели поправка 5 Up первого порядка к невозмущенной амплитуде Up может быть рассчитана по теории возмущений. Полагая, что отклонение правого края щели от вертикальной прямой x = 2 задано функ цией 5 a (у) мы без труда получаем выражение для

5 U p :

b

5Up = 2П • J dy^a(y) • u0 • e'^ • e'kyy • exp(ik. (X - a)2 + (Y - y)2 + Z2)

(X - 2)² + (Y - y)² + Z²

Интеграл (7) легко оценивается методом стационарной фазы:

k

5 U = -z- • u, ^p

exP^(ikZ R + ik x a)

о •-------- • W) •

ZR

• ^ ^Z R ^ exP('k y Y ^{- k}2Z R ) • { [ C ( П + ) ⁺ C ( П - ) ] ⁺

+ i [ 5 (П+) + 5 (n-)]} где в свою очередь

Z r = X - 2)² + Z²,

/+= п	-(b + ^Y) Z R 2
n - = п	—(b - "Y) Z R 2

Y + k y Z R. , - b <  Y <  b k ^,22

b ^Y >  b

• 2^,      2

  - b , Y <- b 22

причем δ R a ( Y )=0 при | Y |>= b /2.

Совершенно аналогично вычисляются поправки к амплитуде U p , обусловленные непрямолинейностью остальных сторон квазипрямоугольной щели.

Формулы (4) - (10) полностью решают поставленную задачу о нахождении амплитуды (или интенсивности) дифрагированного на КШ света в каждой точке фотоприемнике.

Оптическая функция отклика U _m( x ) представляет собой интеграл от задаваемой формулой (4) интенсивности I p (с учетом поправок типа (8)) по площади фотоприемника. Этот интеграл может быть вычислен аналитически, но поскольку ответ чрезвычайно громоздок и выражается в виде разложения в ряд по вырожденным гипергеометрическим функциям, мы не приводим его в настоящей статье.

• 3.    РЕЗУЛЬТАТЫ РАСЧЕТОВ

• 4.    ЗАКЛЮЧЕНИЕ

На рис. 3, 4 представлены результаты численных расчетов интенсивности I p и суммарного сигнала U m ( x ) для случая падения зеленого света ( Х =0.5 мкм) на бесконечно длинную щель шириной a =50 мкм при наличии зазора между КШ и СчЭ d =50

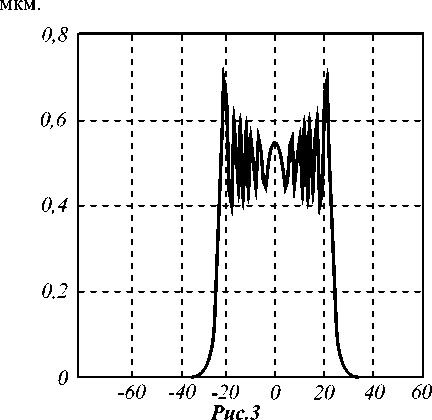
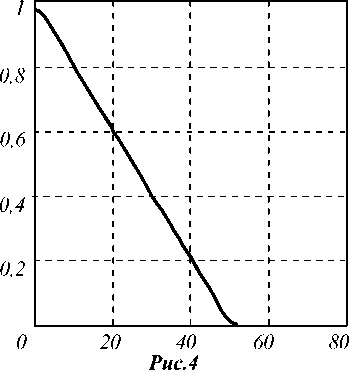
Из рисунков хорошо видно, что дифракционная картина носит ярко выраженный френелевский характер. Оптическая функция отклика Um(x) нелинейна при малых x, что позволяет сделать вывод об актуальности рассматриваемой в статье задачи, поскольку наибольшие относительные погрешности датчиковая аппаратура выдает именно для малых значений угловых или линейных перемещений, наиболее интересных с прикладной точки зрения. Многочисленные расчеты, не приводимые в настоящей статье, показали, что вариации длин волн падающего света, а также замена монохроматического пучка на белый свет не меняют основных качественных выводов.

Резюмируем вышесказанное следующим образом: