Дифракция упругих волн и рассеяние энергии в композитах со случайными структурами

A self-consistent statistical mechanics approach is developed for determining the effective elastic properties of composites with random structure. The problem is reduced to the model of a single inclusion with a nonhomogeneous elastic neighbourhood in a medium with effective dynamic elastic properties. The nonhomogeneous elastic properties and size of neighbourhood are defined by randomness of the geometry’, random size of inclusions and random elastic properties of the inclusions. Numerical results are given for the effective dynamic elastic properties of a composite with unidirectional hollow fibres.

1.    Микро и макроуровни композита

Понятие элементарного объема V в динамике рассеивающих сред вводится как объем, в котором количество поглощенной и рассеянной энергии волн пропорционально его размеру [3]. Для этого необходимо, чтобы он был, с одной стороны, достаточно велик, т е. чтобы статистические характеристики распространения волн были близки к средним, а с другой - мал, чтобы интенсивность падающей на него волны оставалась почти неизменной в его пределах.

Будем рассматривать распространение и эффект затухания гармонических волн в матричных композитах, например, когда все включения имеют одинаковые геометрическую форму, ориентацию, размер и выполняются условия идеального контакта на межфазных поверхностях. Пусть плотности включений p_F и матрицы p_v равны между собой, p_F = р_м = р .

В области V на микроуровне композита имеем уравнения движения вида или с учетом разложений

«, О, 0 = u_w W^’ .       ^„ f, 0 = а_(а)у (.rV”¹

имеем уравнения

(г)и,_а)т„ (г)^ + рю ²u_W1 (г) = 0                      (1)

относительно комплексных амплитуд смещений u_(afr) гармонических колебаний при условии отсутствия вариаций плотности р в композите, го - круговая частота Поле упругих свойств С(г) в (1) имеет вид

C_ijmn (f) = O_F (r)C,^_n + (1 - ©_F (r))c,X„,                    (2)

где CF и CM - тензоры упругих свойств включений и матрицы, индикаторная функция включений

1, е ^

О, г g F/ где VF - область включений в V .

Рассмотрим вычисление тензора динамических эффективных упругих свойств С* композита, входящего в обобщенный закон Гука на макроуровне композита,

О ‘ (г, t) = (Г Е * (Г, где макронапряжения ст*(гД) =<ст|; (г,/) > и макродеформации е*(г,/) =< е. (r,Z) >, оператор объемного осреднения

В результате из формул (2) и (3) получим выражение для расчета тензора

Сути = Сц_тп + v_F(C_ljpq - C^_pq )N_(a)pqmni                  (4)

где v_F - относительное объемное содержание включений в композите, Л’^. - тензоры концентраций осредненных комплексных амплитуд деформаций на включениях

^{< е}(а)у(^Г) ^>F ⁼ (аЗДтп⁶(Дтп >                                    (5)

где <... >_F - оператор объемного осреднения по области включений V_F композита.

Таким образом, задача расчета тензора динамических эффективных упругих свойств С" композита сводится к расчету тензора концентраций осредненных комплексных амплитуд деформаций на включениях N^. Рассмотрим вычисление тензоров N?a) из решения соответствующей осредненной краевой задачи обобщенного метода самосогласования.

2.    Постановка осредненной задачи обобщенного метода самосогласования

В локальной системе координат к-го включения введем в рассмотрение поля u^jfiU, s^® и ^а)^), связанные с соответствующими полями в глобальной системе координат г соотношениями где r,^ - радиус-вектор центра Л-го включения в области V; уравнение (1) примет вид

1 N после осреднения которого оператором —^... получим

N t=i

^a>,?./U + pto2wfa>/^ = 0,                        (6)

где осредненные поля комплексных амплитуд перемещений и напряжений wy= i-рм^- F^^i^i,^ ■

Аналогично введем в рассмотрение осредненное поле амплитуд деформаций через которое можно рассчитать значения тензора N^ из соотношения (5)

< eWij(r)>F =          - —у f Js ?Хо^о<®,

0 0

где v=l,2 , например, когда плоскость поляризации волн совпадает с трансверсальной плоскостью г, Or. однонаправленного волокнистого композита, £_о =1^1 ^и ® -полярные локальные координаты. Через найденные значения тензора N^? может быть рассчитан тензор эффективных динамических упругих свойств композита С* (4).

Таким образом, поля н(о)(^), фа;(^) и а^/О^ гДе

£(a)yf^ U(a)(i,j)CU '

^(a)ij^)  а( ajymn^^f a)miX^ > могул быть определены из решения осредненной задачи вида

^(а^^^^, + P®²«_foV/^ = О,         (7)

поле упругих свойств которой

^(ЦС^-t№^X«)db^^^  (8)

где структурные функции:

VF                    l-vF учитывают ближний порядок взаимного расположения включений через осредненную индикаторную функцию

W *=]

А:’^) - тензорное поле, обратное

W^ = Ш)Е_утп +(i^>-M>)v^№         <⁹)

Расчетная схема осредненной задачи - дифракция продольной и поперечной волн, падающих на расположенное в среде с искомыми эффективными динамическими упругими свойствами одиночное включение, окруженное переходным слоем с неоднородными упругими свойствами.

3.    Однонаправленный волокнистый композит

Рассмотрим распространение продольных и поперечных гармонических волн в плоскости изотропии ^ Ог_г однонаправленного волокнистого композита в условиях плоской деформации (рис. 1).

Для численного решения осредненной задачи будем использовать цилиндрическую систему координат ^0,0,£3 и представим расчетную область (рис.2) в

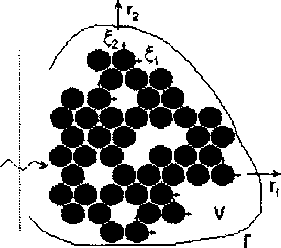
Рис. 1. Представительная область композита в плоскости изотропии

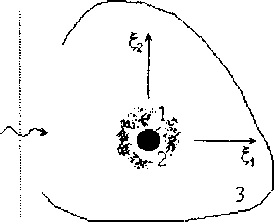
Рис 2. Расчетная схема обобщенного метода самосогласования: 1 - волокно, 2 - неоднородная окрестность, 3 -однородная эффективная среда виде совокупности N=50 концентрических цилиндрических слоев с однородными изотропными упругими свойствами; при этом переходный цилиндрический слой с изотропными в каждой точке Е, и неоднородными по радиальной координате Е„ = |Е,| упругими свойствами д(д)(^0) дискретизировался HaAf-F-l тонких слоях.

Эффективные динамические упругие компоненты С* и сечения рассеяния у* в плоскости изотропии волокнистого композита

Эффективные константы	Результаты расчета
	статический [1]	динамический
kllll/L 1111	3,09	1,39
^1212' ^'1212	3,01	1,45
	-	5,99
	-	8,84

Результаты численного расчета компонент С*_|П и С*_т тензора С* эффективных динамических упругих свойств в плоскости изотропии г_х Ог₂ представлены в таблице, когда круговая частота о = 600с^-1 и относительное объемное содержание волокон в композите v_F = 0,5. Модули Юнга и коэффициенты Пуассона изотропных матрицы Е_м=\ ГПа, v_iV=0,15 и волокон E_F=V№E_M, v_F=0,l при значении отношения £^/р = 10⁶ . Когда круговая частота со <20 с^-1, тогда численные значения компонент С*_ш или C_Uvz» полученные обобщенным методом самосогласования с учетом и без учета [1, 2] динамических эффектов, различаются менее, чем на 3%.

Численные значения эффективных сечений рассеяния у* приведены в таблице для распространяющейся вдоль оси г, продольной (у,*) или поперечной (у^) волн в плоскости изотропии Г] От2 однонаправленного волокнистого композита. Величина у* рассчитана из уравнения где /* - интенсивность падающей волны, рассеянная энергия за единицу времени

^£ ~ "A J \^a(a)%^U(a)t ^{+ a}(a)t6^U(a;9

'(a>6,eM(a)6

4  0

для R»r_F, символ • обозначает комплексно сопряженные величины

Заключение

Рассмотрено решение задачи прогнозирования тензора эффективных динамических упругих свойств и эффективных сечений рассеяния для композитов со случайными структурами обобщенным методом самосогласования. Задача сведена к соответствующей более простой осредненной краевой задаче, расчетная схема которой - дифракция продольной и поперечной волн, падающих на расположенное в среде с искомыми эффективными динамическими упругими свойствами одиночное включение, окруженное переходным слоем с неоднородными упругими свойствами. Представлены результаты численного расчета компонент тензора С* эффективных динамических упругих свойств и эффективных сечений рассеяния у* продольной и поперечной волн в плоскости изотропии однонаправленного волокнистого композита.