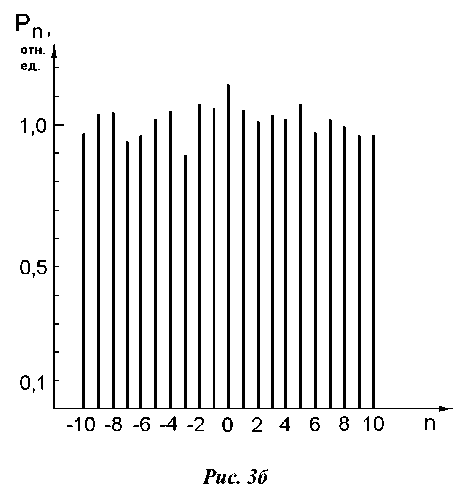Дифракционные оптические делители пучка

Делители пучка, осуществляющие деление исходного плоского пучка излучения на заданное количество частей (порядков) таким образом, чтобы отношения интенсивностей излучения, распространяющегося в различных порядках, принимали заданные значения являются одними из наиболее простых дифракционных оптических элементов [1]. Делители пучка используются во многих практических задачах, возникающих в голографии, интегральной оптике, оптической обработке информации, оптической томографии, при трёхразмерном контроле изделий (объектов) и других областях современной оптики.

Целью настоящей работы является решение задачи синтеза дифракционного оптического элемента, способного разделить исходный плоский пучок на заданное количество частей, а именно, дифракционных порядков, расположенных в одной плоскости, и обладающих равными энергиями.

Постановка задачи.

Задачи расчёта и изготовления дифракционных оптических делителей пучка рассматривались и ранее в работах [2,3,4,5]. Впервые возможность решения задачи такого типа была обоснована в [2], где сообщается о получении фазовой двухуровневой линейной дифракционной решётки с равными энергиями в порядках -L, ..., 0, ..., +L. Выравнивание интенсивностей достигалось за счет варьирования профиля периода решетки, что приводило к необходимости решать нелинейную систему уравнений с размерностью, равной L, в предположении симметричности фазовой функции периода. Авторам удалось получить решения с величиной L до 8. В дальнейшем Ю.Г.Туркевич и С.Т. Бобров [3] получили решение этой задачи с величиной L до 11, и, переходя к нессиметрично-му профилю периода, [4] они же увеличили количество порядков до 17, однако при этом размерность нелинейной системы уравнений возрасла. И, хотя несимметричное решение допускает примерно в 2 раза больший уход размеров рельефа в периоде решётки от номинала, чем симметричное, данные, приведённые в [4] свидетельствуют о том, что даже для теоретических спектров отклонение интенсивностей в боковых рабочих порядках от интенсивности, средней по порядкам, составило ±9%. Лучшее теоретическое выравнивание интенсивностей (до 1-2 %) удалось достичь в работе [5] путём введения дискретизации фазовой функции и квантования на произвольное число уровней, однако изготовление таких элементов вызывает зна- чительные трудности.

Интенсивность Il излучения в l-ом порядке дифракции двухуровневой линейной дифракционной решетки с периодом T, показанной на рис.1, полностью определяется рельефом одного периода (профилем периода решётки) и описывается следую- щим известным решением:

1 1 =

( C l + S l ) ( л l ) ²

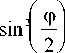
l * 0,

1 0 = 1 - 4Q ( 1 - Q ) Sin 2 [|] ,

C = £ ( - 1 ) ’ cos ( 2 n lx . ) , n = l 2 N

S i = £ ( - 1 ) " sin ⁽ 2 n lx„ ) , n = l

2 N

Q = E(- 1) "x n= l ф=

2 n d ( v - 1 ) X

где x n - координаты границ канавок в профиле периода решётки, N - количество канавок в периоде, А - глубина канавки, X - длина световой волны, v -показатель преломления материала подложки.

Профиль штриха двухуровневой периодической дифракционной решетки (N=4).

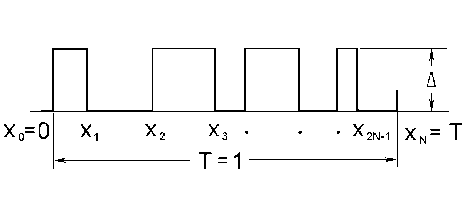
Рис. 1

Выравнивание интенсивностей достигается за счет варьирования профиля периода решетки, а именно, за счет задания положений точек разрыва (границ канавок).

Именно такая постановка задачи обусловлена имеющейся технологией [6] изготовления дифракционных оптических элементов. Отличие настоящей работы от предшествующих заключается в том, что мы свели задачу решения системы нелинейных уравнений к задаче минимизации функции качества и учли технологические требования непосредственно в процессе расчета элемента, что привело к фактически полному теоретическому выравниванию интенсивностей рабочих порядков и лучшему соответствию расчетных и экспериментально полученных значений интенсивностей порядков дифракции.

Рассмотрение задачи оптимизации профиля штриха.

Качество делителя пучка определяется двумя параметрами: полной дифракционной эффективностью (количеством энергии, которая направляется во все рабочие поряки), и степенью равномерности распределения энергии по рабочим порядкам.

Наиболее технологичным является решение, в котором в профиле периода решётки канавки имеют одинаковые или близкие размеры, а так же отсутствуют канавки с такими размерами, которые не могут быть изготовлены на существующем оборудовании.

В связи с вышесказанным, математическая задача определения положения точек разрыва в профиле штриха рассматривалась нами как задача минимизации следующей функции качества:

f ( x 1 ,

•••’ x 2 n - 1 )

L - 1

iо+Z( i+1 -i )2

+

+ в

2 N - 1

x/2 + (1 - x 2 N-1 ) + £ ( xn+1 - xn )

n = 1

Функция качества состоит из двух слагаемых. Решение задачи представляет собой глобальный минимум для первого слагаемого. Если нулевой порядок не подавляется , то интенсивность I 0 включается в сумму наравне с другими рабочими порядками. Второе слагаемое позволяет удовлетворить технологическим требованиям. Функция является аналитической и производные первого и второго порядка существуют и ограничены.

В разработанном пакете прикладных программ для численного поиска минимума функции качества используется стандартная программа [7] определен-ния минимума функции методом Ньютона второго порядка. Этот метод отличается надежностью, быстродействием и высокой точностью. Матрица Гессе и вектор градиента вычисляются по формулам, полученным при аналитическом дифференцировании функции качества. Расчет проводится на ЭВМ IBM PC, языком программирования служит Фор- тран. Комплекс программ позволяет в диалоговом режиме задавать количество дифракционных порядков, демпфирующий множитель и коэффициент р. Поиск минимума проводится циклами. После каждого цикла выводится величина функции качества. Если эта величина равняется нулю, то решение найдено и массив координат точек разрыва выводится на дисплей и на печать.

Экспериментальные результаты.

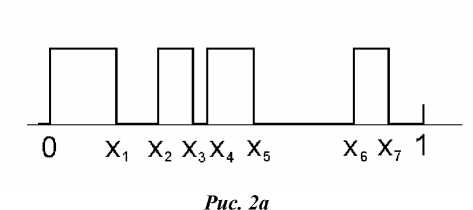
Нам удаётся рассчитывать делители вплодь до 42-х порядков равной интенсивности ( L =21), при этом величина функции качества равна 10^-24. То есть расчетная разница интенсивностей порядков менее 10 ^-12, что значительно превосходит результаты, полученные ранее в [4]. На рис. 2а показан профиль периода дифракционного делителя на 12 порядков.

Профиль периода решётки с 12-ю порядками равной интенсивности . x4 - x3 =0.04.

По стандартной технологии электроннолучевой литографии был изготовлен ряд делителей для излучения с длиной волны 0.63 мкм на стеклянных (К8) подложках с расчетной глубиной канавок 0,6 мкм.

Минимальная ширина канавок для делителей на 21 порядок составила 0,035 х T , а для делителей на 12 порядков - 0,04 х T , где T - основной период решетки. Изготовленные решётки имели следующие периоды: 100 мкм, 150мкм, 390мкм. В процессе изготовления допускались ошибки ширины канавок в пределах ± 1 мкм, а так же ошибки глубины травления - ± 3% и клин травления в пределах 0,3 мкм.

Экспериментальные исследования образцов проводились на оптической скамье. Источником света служил гелий -неоновый лазер. Дифракционный элемент освещался лазерным пучком, энергия в выбранном порядке измерялась измерителем мощности. Распределение интенсивности в поперечном сечении спектра исследовалось с помощью сканера, базирующегося на МДП-интегральной линейке фотодиодов ЛФ1024-25/1 и имеющего 12-разрядный АЦП [8].

Экспериментальное исследование делителей на 12 порядков показало, что интенсивности в рабочих порядках отличаются от интенсивности, усредненной по порядкам, менее чем на 6%. Делители на 21 порядок демонстрировали больший разброс в интенсивностях порядков, он составил 11%. Общая дифракционная эффективность составила 92% для решеток с 12-ю порядками (L=6) равной интенсивности и 83% - для решеток с 21-м порядком. На рис.2б и 3а приведены распределения интенсивностей в спектрах делителей на 12 и 21 порядок, соответственно. Результаты измерения мощности в дифракционных порядках даны на рис. 2в и 3б.

Распределение интенсивности в спектре делителя на 12 порядков. i - нормированная интенсивность, Y - координата вдоль линейки фотоприёмника.

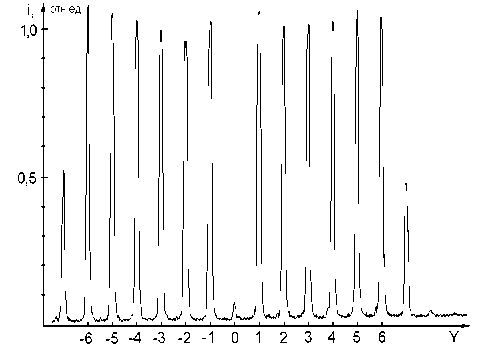
Рис. 2б

Результаты измерения мощности P n порядков n для делителя на 12 порядков. Величина P n нормирована на среднее значение по рабочим порядкам.

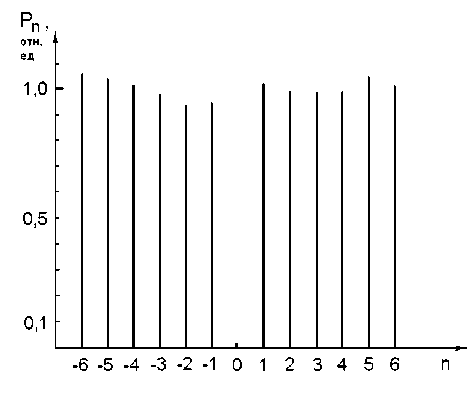
Рис. 2в

Заключение.

Формулируя задачу расчета дифракционных оптических делителей пучка как задачу минимизации функции качества, и определяя соответствующим образом эту функцию, нам удалось провести оптимизацию профиля периода дифракционной решётки, осуществляющей деление падающего светового пучка на порядки равной интенсивности вплодь до 42-х порядков , с величиной функции качества менее 10 -24. Экспериментальное исследование изготовленных образцов показало, что даже ошибки, значительные (до 25%) по отношению к ширине канавки, наиболее узкой в периоде решетки, не приводят к катастрофическим последствиям для распределения интенсивности по порядкам дифракции. Так разброс в интенсивностях рабочих порядков делителя на 12 пучков составил 6%. Этот факт характеризует большую устойчивость полученного решения.

Распределение интенсивности в спектре решётки с 21-им порядком равной интенсивности . i -нормированная интенсивность , Y - координата вдоль линейки фотоприёмника.

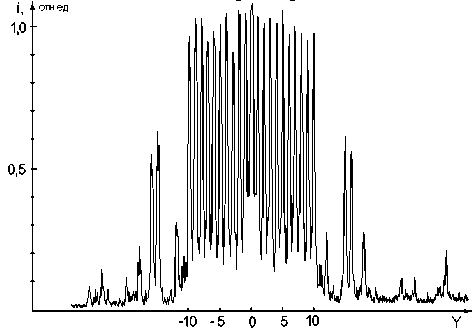
Рис. 3а

Результаты измерения мощности P n порядков n для делителя на 21 порядок. Величина Pn нормирована на среднее значение по рабочим порядкам.