Дифракционные оптические элементы, согласованные с модами Гаусса-Лагерра

Моды определяются как устойчивые при распространении в волноводной среде световые пучки. Моды не расплываются и не изменяют пространственной структуры в процессе распространения в своей среде, а лишь приобретают фазовый набег [1].

Рассматриваемые моды Гаусса-Лагерра сохраняют свою структуру и в свободном пространстве, изменяясь лишь масштабно.

Актуальной задачей является создание приборов, формирующих эталоны модовых пучков, и приборов, измеряющих модовый состав имеющихся многомодовых пучков. Такие приборы смогут осуществить индивидуальное возбуждение, измерение и обнаружение мод когерентного излучения.

В работах [1-3] в качестве таких приборов рассматриваются дифракционные оптические элементы (ДОЭ), рассчитанные с помощью методов компьютерной оптики. Особый интерес представляют фазовые ДОЭ, имеющие повышенную энергетическую эффективность и многоканальный характер работы, позволяющий сформировать несколько модовых пучков.

В отличие от метода кодирования с пространственной несущей частотой, рассмотренного в [1], и итеративного метода с использованием вспомогательной области, приведенного в [2], в данной работе используется метод, разработанный в [3]. Он состоит в итеративной аппроксимации функции пропускания ДОЭ конечной суммой гауссовых мод. Однако, в [3,4] были рассмотрены только радиально-симметричные моды Гаусса-Лагерра. В данной работе этот метод применен к обобщенным модам Гаусса-Лагерра. Такое расширение метода позволяет с высокой эффективностью формировать модовые пучки, поперечное сечение которых представляет собой заданное изображение.

Кроме того, хотя рассматриваемый метод работает тем лучше, чем больше задействовано мод в пучке, он работоспособен и при формировании одномодового пучка. В этом случае за одну итерацию получается ДОЭ с фазовой функцией, пропорциональной знаковой функции моды. Показано, что для эффективного формирования отдельных мод Гаусса-Лагерра можно использовать фазовые элементы, пропускание которых равно знаковой функции соответствующего многочлена Лагерра.

1. Итеративный алгоритм расчета фазовых формирователей пучков Гаусса-Лагерра

Алгоритм, рассмотренный в [3,4], в случае обобщенных мод Гаусса-Лагерра выглядит следующим образом. Задача состоит в том, чтобы рассчитать фазу ф (x,y ) дифракционного оптического элемента, удовлетворяющую соотношению

A о ( x , У )ехр [ г ф ( x , у ) ] =

N

= SS C nm S nm ( r , 6 ) ’ n = 0 m <  n

(1.1)

в котором S _nm ( r , 0 ) - обобщенная функция Гаусса-Лагерра:

S nm ( Г , 6 ) =

2 ^п ( n - m ).

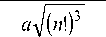
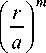
X

(1.2)

x ехр [ - ( rja ) ² /2 L m ( ( r/a ) ² ) exp [ ± im 6 ]

2       2 ,    2 _Q , ^y

r = x + у , 0= arctg—

x dm где Ln (x) = (-1) ----[L + (x)] - обобщенный мно- dxm гочлен Лагерра, A0(x, у) - известная амплитуда освещающего пучка, модули коэффициентов |Cnm | задаются произвольно, а аргументы Cnm являются свободными параметрами задачи. Квадраты модулей коэффициентов |Cnm|2 характеризуют энергетический вклад каждой моды в пучок.

Функции Гаусса-Лагерра ортогональны

2 п х

J J S nm ( r , 6 ) S kl ( r , 6 ) r d r d 6 = 5^5, 0 0

(1.3)

[ 1, n = m где o _nm = <         - символ Кронекера.

[ 0, n * m

Для удобства перепишем уравнение (1.1) в полярных координатах ( r, 6 ):

f ( r , 6 ) = A 0 ( r , 6 ) exp [ i ф ( r , 6 ) ] =

= f S C ,„ S „„ ( r 6

n = 0 m <  n

(1.4)

Тогда коэффициенты в уравнении (1.4) вычисляются по формуле:

2 п х

^Cnm = J f A 0 ⁽ r , ^{6 ) еХ}Р^{[ ф (} r , ^{6 )]х}             ., „

00                                   (1.5)

^х S nm ^{( r , 6 ) r d r d 6}

Предлагаемый итеративный алгоритм основан на последовательном вычислении сумм (1.4) и интегралов (1.5) с помощью алгоритма быстрого преобразования Фурье с наложением соответствующих ограничений. Так, на к -ой итерации рассчитанные коэффициенты с П m ) заменяются на C nmk ) следующим образом

С ^{( к} )=D С^{( к )}|с^{( к} ) Г* nm nm nm nm ^{,                            .}

где Dnm - неотрицательные числа, характеризующие распределение энергии между модами. Огра- ничения типа (1.6) характерны для итеративного алгоритма Герчберга-Секстона [5]. Однако, для улучшения сходимости можно применять модификации замены (1.6), вводя некоторый коэффициент адаптивности 0< а < 1:

[Dnm - «СПк?| - Dnm )]х х Cn m) \cm)| "*,( „, m) eQ 0 ,(n, m) gQ

|[Dnm — «f    — Dnm IX

C™ ) =‘     х C nm C nm>\ Л( n , m ) _eQ ,

СПm ,( n , m ) gQ

(1.7)

(1.8)

где Q - множество пар индексов, для которых отличны от нуля числа D nm .

Таким образом, можно предложить следующий алгоритм для нахождения фазы оптического элемента ф (г,0).

• 1.    Начальная фаза выбирается как случайная величина ф ₀ (г, ^ .

• 2.    Пусть на k -ом шаге по формуле (1.4) получается значение к -ой фазы: ф _k (r, 0 ). Используя ф к (г, 0 ) , из уравнения (1.5) рассчитываются коэффициенты C _n ⁽ _m ^{k )} .

• 3.    Затем они заменяются коэффициентами C _n ⁽ _m ^{k )} , используя правило (1.6), (1.7) или (1.8).

• 4.    Коэффициенты C _n ⁽ _m ^{k )} подставляются в (1.4).

В результате получается функция f(r, 9 ) , аргумент которой служит последующей оценкой фазы

N fk (r ,6) =ZZ Cnm) Snm (r, 6), n=0 m < n

.

(1.9)

Ф к + 1 ^{( r , 6 )} = arg { fk ^{( r , 6 ) }}

Переходим к 2. И так далее.

Сходимость алгоритма контролируется по средним отклонениям:

2 п ю

§ A =

_ 0 0

' 2 r d r d 0\

X

,

(1.10)

X <

JJ A 2 I г ^{, 6} ) ^r d ^r d ⁶

. 0 0

I N                „,|12 1 2

§ = ^ZZDnm - Cnm |] [ X

L n = 0 m <  n

(1.11)

,

I

X^ ZZ D nm

L n = 0 m <  n

Аналогично тому как это сделано в [4], можно показать, что ошибки (1.10) и (1.11) не возрастают:

§ A^{k + 1)} <  § A^k ) , § C^{k + 1)} <  § C^k ) .                    (1.12)

Функции Гаусса-Лагерра являются собственными функциями преобразования Фурье:

J J S nm ( r , 6 ) exp [ - ir p cos( 6 - V ) ] r d r d 6 = ^{2 n} 0 0                                              , ⁽1.1³⁾

= (-1)n (- i) mSm (p,v)

что позволяет использовать их для эффективного ввода излучения в световые волокна [1]. Так, если мы сформировали световой пучок, сечение которого имеет вид заданного изображения, и который является суперпозицией мод Гаусса-Ла-герра:

N g ( r ,6 ) =ZZ CnmSnm ( r ,6 ), n =0 m < n

(1.14)

то в зоне дифракции Фраунгофера или в фокальной плоскости линзы мы получим следующее изображение:

3{ g(r ,6)} = G(p,v) =

= 22 Z ln„CnmS.m (p,v)’ n=0 m < n

(1.15)

где 3 - обозначение Фурье-преобразования.

Следовательно, если в суперпозиции участвовали только моды с одинаковыми значениями собственных чисел

A nm = ( - 1) n ( - i ) m = ^ 0 ,

(1.16)

то вид изображения в сечении пучка не меняется.

Из формулы (1.16) видно, что собственные числа функций Гаусса-Лагерра принимают всего четыре значения:

Anm = 1: (n = 2к, m = 41),(n = 2к +1, m = 41 + 2),

Anm = -1: (n = 2к,m = 41 + 2),(n = 2к +1, m = 41),

A _nm = i : ( n = 2 к , m = 4 1 + 3),( n = 2 к + 1, m = 4 1 + 1),

A _nm = - i : ( n = 2 к , m = 4 1 + 1),( n = 2 к + 1, m = 4 1 + 3), к , 1 = 0,1,2,...

(1.17)

Более наглядно распределение одинаковых значений собственных чисел в зависимости от номера функции Гаусса-Лагерра приведено в Таблице 1.

Таким образом, вполне реально подобрать такую суперпозицию мод Гаусса-Лагерра с одинаковыми собственными значениями, чтобы сформировать некоторое изображение, не меняющее своей структуры при прохождении Фурье-каскада. Заметим, что функции Гаусса-Ла-герра с взаимно противоположной «закруткой» exp[ ± im 9 ] имеют одинаковые собственные значения.

Таблица 1. Собственные значения для собственных функций Гаусса-Лагерра

m n	0	1	2	3	4	5	6	7	8	9
0	1
1	-1	i
2	1	-i	-1
3	-1	i	1	-i
4	1	-i	-1	i	1
5	-1	i	1	-i	-1	i
6	1	-i	-1	i	1	-i	-1
7	-1	i	1	-i	-1	i	1	-i
8	1	-i	-1	i	1	-i	-1	i	1
9	-1	i	1	-i	-1	i	1	-i	-1	i

Совокупность мод Гаусса-Лагерра с одинаковыми собственными значениями можно считать модовой группой, так как она также представляет собой собственную функцию преобразования Фурье.

(p-q! ^да sgn [ L m ( t ) ] L^q p ( t ) • t^q e ^- t d t x (2.4) ( p) 0

2. Фазовые формирователи одномодовых пучков Гаусса-Лагерра

Понятно, что рассматриваемый метод работает тем лучше, чем больше задействовано членов в сумме (1.4), а следовательно мод в пучке. Имея больше степеней свободы, которыми являются фазы коэффициентов C nm , мы точнее аппроксимируем желаемую функцию f(r , 9 ), в частности, амплитуду рассчитываемого ДОЭ A 0 ( x , у ).

Однако, данный метод работоспособен и при формировании одномодового пучка. В этом случае за одну итерацию (с дальнейшей стагнацией) конструируется ДОЭ с фазой, пропорциональной знаковой функции от многочлена Лагерра:

^( r ,0 ) = arg{Snm(r ,9 )} =

= у ^{( 1 -} sgn L m ⁽⁽ ria ^{) 2 )]} ) ± im ⁹              ( )

Покажем, что такая аппроксимация функции Гаусса-Лагерра является эффективной.

Выражение (2.1) для фазовой функции эквивалентно следующему выражению для амплитуды на участке [- R , R ], где R - размер апертуры, t =( r/a ) ² :

S nm ( t, 9 ) = sgn [ L m ( t ) ] exp( ± im 9 )           (2.2)

= . R" ¹ f l sgn [ L " ( t ) ] L mp ( t ) x

N ⁽ p ^!) 1 0

x t^m e ^- t d t ) = С Г)

Таким образом, ненулевыми являются только коэффициенты с таким же вторым индексом, что и раскладываемая функция S_nm ( t , 9 ).

Обозначив через t _k,_n нули многочлена L m ( t _kn ) = 0 и считая t ₀,_n =0, представим выражение (2.4) в виде суммы интегралов:

уА( n , m )

^C pm

n - 1

xZ

k = 0

( p - m )! ( p !)³

( - 1) ^k J t^m e ^- t L m ( t )d t t kn

(2.5)

С учетом справочного интеграла [6]:

f x ^a e - ^x L “_n ( x )d x = -x^{a + 1} e - ^x L ^ ⁺J ( x )        (2.6)

n

вместо (2.5) получим следующее выражение для коэффициентов разложения (2.3):

A¹! n , m )

^C pm

2 I ( p - m )! pn ⁽ p ^!)3

x^ T [ ( - 1) ^{k - 1}( t kn ) ^{m + 1} e ^{- tk} n L m - 1 ( t k , n ) ] k = 1

(2.7)

Разложим функцию (2.2) по ортогональным многочленам Лагерра с «закруткой»:

да

S nm ( t , 9 ) = ZZ C pm ) L p ( t ) exp( ± iq 9)       (2.3)

p=0 q < p и найдем коэффициенты разложения:

да

C T) =_А q J Jsgn [ L m ( t ) ] e ± m ⁹ x

N ⁽ p ^!) 0 0

x L p ( t )e ^{T iq 9} t^q e ^- t d t d 9 =

При этом коэффициенты ( 2^{_рⁿm ) с q * m равны нулю.

Рассмотрим пример. Пусть требуется сформировать моду Гаусса-Лагерра S ₁₀ ( t , 9 ) . Для этого разместим в плоскости z=0 фазовый элемент с пропусканием ,S ₁₀ ( t ) = sgn [ L 0 ( t ) ] . Тогда, согласно уравнению (2.7) в пространстве за фильтром сформируется суперпозиция световых мод:

да s (t) = 2 C^l\ (t) = p=1

= 0,736 ■ L 0 ( t ) - 0,184 ■ L 2 ( t ) +                 (2.8)

+ 0,020 ■ L 3 ( t ) - 0,001 - L 4 ( t ) + ...

Освещая такой фазовый элемент коллимированным гауссовым пучком, получим согласно уравнению (1.13) в частотной плоскости световое поле с амплитудой, пропорциональной выражению ( a =1 мм):

да

J e-r/2 sgn [L (r2)] J0 (rp )■ r d r = да

= 2(-1) "<%’e-pk Lp (p ’) = p=1

= - e - ^{p /2} [ 0,736 ■ L 0 ( p ²) + 0,184 ■ L 0 ( p ²) +

^L                                       , (2.9)

+ 0,020 ■ L 0 ( p ²) + 0,001 L 4 ( p ²) + ... ]

где J 0 ( x ) - функция Бесселя.

Отношение энергий световых пучков, описываемых вторым и первым слагаемыми в уравнении (2.9) равно:

(0,184) 2 ^да e ^{- p 2} [ L 0 ( p ² ) ] 2 ■ p d p 0

(0,736) 2 ^да e ^{- p 2} [ l 0 ( p ² ) ] 2 ■ p d p 0

+          2    * 0,25

(0,736) ² (1!) ²

Таким образом, в первом слагаемом суммы (2.9), описывающем моду Гаусса-Лагерра 5* 10(t, 0), содержится более 70% всей энергии светового пучка.

Еще более эффективным способом формирования моды Гаусса-Лагерра Snm (r, 0) является освещение не гауссовым, а плоским световым пучком фазового ДОЭ с пропусканием (a=1 мм):

^Snm ^{( r , 6} ) = circ f ^r ) sgnV m ^{( r} 2 ^{)] e}xP⁽ ± im ⁶ ) ⁽2.^{1 0)} к R J

. Г t ) [1, t < 10 где circ I — I = <         .

к 1 0 J [ 0, t >  1 0

В этом случае значение R следует выбирать так, чтобы выражение, определяющее эффективность:

E =

² f ^R S _nm ( r , 6 ) ■ s ;_m ( r , 6 ) r d r d6

2 n R            2           2 п да

J J | 5 „_и ( r , 6 )| r d r d9^ J J | 5 „_m ( r , 6 )| 2 r d r d 6

(2.11)

было максимальным.

Рассмотрим пример с модой Гаусса-Лагерра S ₁₀ ( t , 0 ) . В этом случае выражение (2.11) записывается следующим образом:

2 ■

E =

J e ^r ^² ( 1 - r ² ) r d r - J e r ^² ( 1 - r ² ) r d r 01

R ²

= (2.12)

4 ■ [1,426 - e ^{- R 2 2} ( R ² + 1 ) ] ²

R ²

и достигает максимального значения E =0,786 при R =2,5 мм. Значит, световое поле (2.10) формирует моду Гаусса-Лагерра S ₁₀ ( r , 6 ) с эффективностью около 79%.

3. Численные примеры

При численном моделировании использовались следующие параметры: 128 отсчетов по радиусу r и 128 отсчетов по угловой составляющей 0 , диапазон изменения аргументов r е [0,7мм], 0е [0,2 л ], длина волны Х =0.63 мкм, фокусное расстояние f =100 мм, радиус гауссового пучка в перетяжке a =1 мм. В формулах (1.4) и (3.3) рассматривались члены ряда с номерами n,m <  N =7.

Действие рассчитанных ДОЭ моделировалось с помощью численного преобразования Фурье (1.13).

На рис. 1 представлены результаты формирования моды Гаусса-Лагерра (3,2). Фазовая функция (рис. 1а) рассчитывалась по формуле (2.10). На рис. 1б показан сформированный таким ДОЭ пучок и для сравнения на рис. 1в приведена эталонная мода Гаусса-Лагерра (3,2). Их радиальные сечения показаны на рис. 1г (сплошная линия - рассчитанная мода, пунктирная линия - эталонная мода).

Оптимальный радиус апертуры R определялся из условия максимизации эффективности E (2.11) сформированного пучка. График зависимости E от R для моды Гаусса-Лагерра (3,2) представлен на рис.2. Из графика видно, что оптимальный размер апертуры ДОЭ для формирования моды Гаусса-Лагерра (3,2) равен R =4,5 мм. При этом эффективность достигает значения 81%.

Проведя аналогичные исследования можно подобрать оптимальный радиус ДОЭ для формирования любой моды. С помощью численного моделирования было показано, что фазовые ДОЭ, рассчитанные по формуле (2.10) позволяют формировать одномодовые пучки с эффективностью 77-81% в зависимости от номера моды. В следующей таблице приведены значения R и E для нескольких мод.

а)                            б)                            в)                            г)

Рис. 1. Одномодовый пучок: фаза ДОЭ (а); распределения интенсивности в Фурье-спектре для рассчитанной (б) и эталонной (в) мод Гаусса-Лагерра (3,2); интенсивность в радиальном сечении (г) (сплошная линия - расчет, пунктирная линия - эталон).

Таблица 2. Значения оптимального радиуса апертуры ДОЭ R и эффективности E ( a =1 мм) .

Номер моды Гаусса-Лагерра	(1,0)	(2,1)	(3,2)	(4,2)	(5,1)
Оптимальный радиус R, мм	2,5	4	4,5	4,7	5
Эффективность E, %	79	77	81	78	77

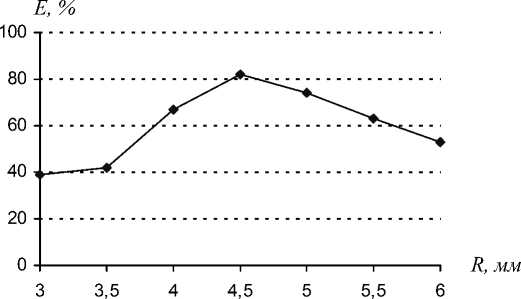
Рис. 2. Зависимость эффективности пучка E от радиуса апертуры R для ДОЭ, формирующего моду Гаусса-Лагерра (3,2).

Можно предположить, что для суперпозиции мод оптимальным радиусом апертуры ДОЭ является средний из оптимальных радиусов входящих в суперпозицию мод.

На рис. 3 приведены примеры фазовых ДОЭ (рис. 3а), формирующих многомодовые пучки Гаусса-Лагерра в плоскости пространственного спектра (рис. 3в). Верхняя строка рисунка относится к группе из 5-ти мод: (1,1), (3,1), (4,-3), (5,1), (5,-5), имеющих собственные числа, равные i. Коэффициенты разложения пучков представлены на рис. 3б в полутонах. Нижняя строка рисунка относится к группе из 6-ти мод: (2,0), (3,-2), (3,2), (4,-4), (4,0), (4,4), имеющих собственные числа, равные 1 . Оба пучка являются собственными функциями преобразования Фурье. Для сравнения на рис. 3г показаны эталонные распределения интенсивности указанных композиций мод.

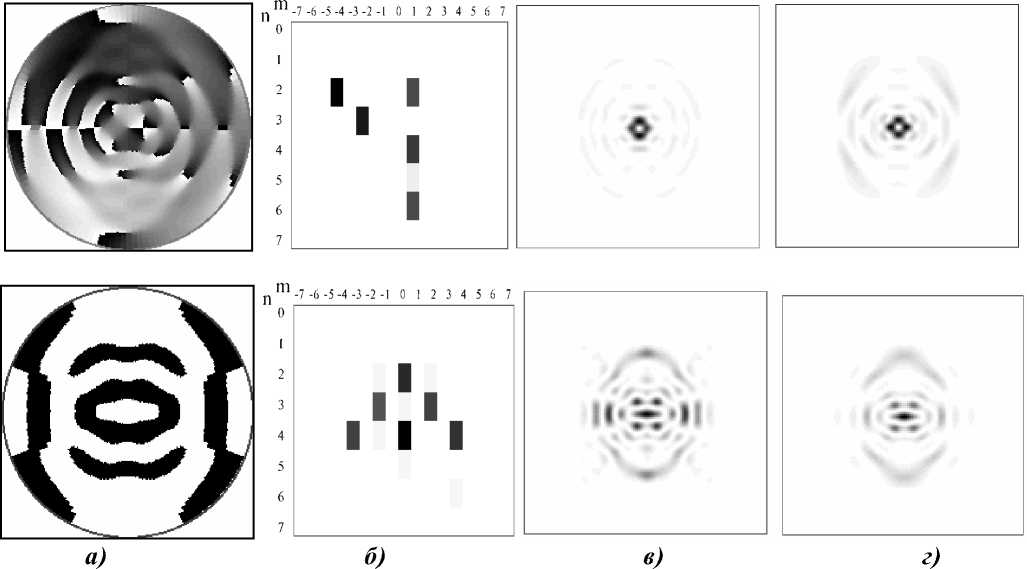
Рис. 3. Многомодовые пучки: фаза ДОЭ (а); квадраты модулей коэффициентов в разложении (1.1) (б); распределения интенсивности в фокальной плоскости для рассчитанной (в) и эталонной (г) композиции мод Гаусса-Лагерра (верхняя строка для 5-ти модового пучка, нижняя строка для 6-ти модового пучка).

Заключение

В данной работе получены следующие результаты:

• -    предложен итеративный алгоритм для расчета фазы дифракционных оптических элементов, формирующих многомодовые пучки Гаусса-Лагерра (уравнения (1.4)-(1.9));

• -    введено понятие групповой моды, как суперпозиции мод Гаусса-Лагерра, не изменяющей своей структуры после прохождения Фурье-каскада (уравнение (1.16));

• -    показано, что для эффективного формирования одномодовых пучков Гаусса-Лагерра можно использовать фазовые элементы, функция пропускания которых пропорциональна знаковой функции от обобщенного многочлена Лагерра (уравнения (2.1) и (2.10)).

Данная работа поддержана Российским фондом фундаментальных исследований (№ 9601-10021 и 96-15-96026).