Дифракционные потери и распределение мощности газоразрядных лазеров по поперечным модам

Дифракционные потери являются важнейшей характеристикой открытого оптического резонатора, так как определяют его свойства как селектора поперечных мод. В классической работе [16] с помощью численного решения интегральных уравнений Ли для поля излучения получены зависимости дифракционных потерь мод ТЕМ 00 и ТЕМ 01 от числа Френеля N и параметра устойчивости резонатора g для симметричного и плоскосферического резонаторов, образованных зеркалами диаметром 2 а .

В многочисленных попытках разработать аналитические методы расчета потерь в сложных многоэлементных резонаторах, применяемых на практике, результаты [16] использовались как численный эксперимент. Так, в работе [12] предложено рассчитывать потери методом эквивалентного конфокального резонатора. Этот метод дает лишь разумную оценку потерь. В работах [4], [13] ограниченные зеркала или диафрагмы с резкими краями (торцы разрядных капилляров) заменялись соответствующим образом подобранными гауссовскими диафрагмами. Этот метод дает хорошие результаты в случае малых чисел Френеля и соответствующих больших дифракционных потерь.

В работах [8], [9] использовался аналитический метод расчета, основанный на принципе Бабине, дающий хорошие результаты при малых потерях за исключением конфигураций резонатора, близких к границе устойчивости. В работе [17] предпринята попытка получения формулы для расчета потерь в резонаторах с одной или несколькими диафрагмами, моделирующими разрядный капилляр. Ошибочность полученных там результатов обусловлена пренебрежением

связью между интегральными уравнениями, описывающими дифракцию излучения в различных частях резонатора.

Подход, предложенный в данной работе, основан на использовании результатов [16] и законов подобия резонаторов. Он позволяет рассчитывать дифракционные потери основной и высших поперечных мод в сложных многоэлементных резонаторах, содержащих гауссовские и негауссовские элементы. Знание дифракционных потерь для мод ТЕМ _pl Λ _l позволяет установить, сколько и какие мо ^p ды генерируют, их распределение по мощности и границу одномодовой генерации, производить расчет таких важных характеристик выходного пучка, как его диаметр и расходимость при заданной конфигурации резонатора, а также определить зависимость выходной мощности от разъюстировки зеркал резонатора.

ДИФРАКЦИОННЫЕ ПОТЕРИ

В ДВУХЗЕРКАЛЬНЫХ РЕЗОНАТОРАХ ПРОИЗВОЛЬНОЙ КОНФИГУРАЦИИ

В работе [11] путем обработки численных данных [16] получены аппроксимационные формулы для расчета потерь ТЕМ₀₀ и ТЕМ₀₁-мод в симметричном (g₁=g₂=g) и плоско-сферическом (g₁ = g, g₂ = 1 или g₁ = g, g₂ = g) резонаторах с зеркалами диаметром 2 а:

exp { - ^ (1-|g) N BC g }

W =     1 + aN ---,    ⁽¹⁾

где A, B, C, a, b – постоянные, отредактированные численные значения которых приведены в таблице; нижними индексами p, l обозначены величины, относящиеся к ТЕМpl-моде, а верхними индексами s и h величины, относящиеся к симметричному и плоско-сферическому резонатору соответственно.

Значения постоянных в формуле (1)

	a	b	A	B	C
ТЕМ s 00	4,86	1,41	5,83	2,1	0,36
ТЕМ h 00	-//-	-//-	2,26	3,08	1,16
ТЕМ s 01	1,62	1,46	3,76	2,05	0,25
ТЕМ h 01	-//-	-//-	0,774	3,28	0,96

На рис. 1а представлены результаты расчетов дифракционных потерь по формуле (1) для моды ТЕМ ₀ ^S ₀ в сравнении с данными [16], иллюстрирующими ее корректность.

Аналогичная точность реализуется и для мод ТЕМ 00 и ТЕМ Sh . Существенным преимуществом формулы (1) по сравнению с предложенными ранее в [3], [5] является отсутствие ограничений на величину N и аналитическая зависимость от g. Отметим, что Л^h ( N,g ) ~ Л^h ( N ,1-|g|), а это позволяет распространить результаты расчета Λ^h на область |g|– 0÷0,5.

Для получения интерполяционной формулы, справедливой во всей области устойчивости резонаторов 0 ≤ g ₁ g ₂ ≤ 1, рассмотрим случай, когда |g₁|>>|g₂|. Отношение радиусов пучка основной моды на зеркалах w ₁/ w ₂, рассчитанное для двухзеркального резонатора без диафрагм, согласно [14], равно: ^g₂ / g 1 << 1 или w 1 << w 2 .

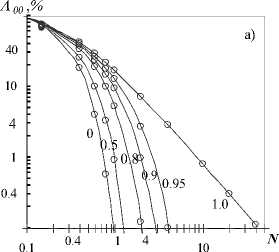
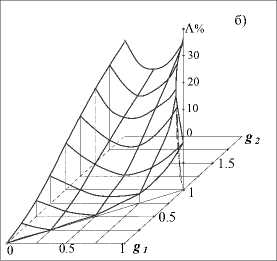
Рис. 1. а) Зависимость дифракционных потерь моды TEM ₀₀ от числа Френеля N для симметричного резонатора: численный расчет [1], ° - расчет по аппроксимационной формуле (1). Цифры у кривых - значения g.

б) Зависимость дифракционных потерь Λ ₀₀ от параметров устойчивости резонатора g ₁ и g ₂ при N = 1

Поскольку для генерации радиус w ₂ должен быть сравним с а , то w ₁<< а и в интегральных уравнениях, описывающих поле излучения в резонаторе, можно заменить конечный радиус первого зеркала на бесконечный. Задача о нахождении потерь при этом сводится к известному случаю резонатора с одним диафрагмированным зерка лом [15]:

^л№д_vg 2 ) • ^л(^ ,gj = 1- ¹ - ^л( N .gj,^

2| g ₁      q \          2| g ₁       q

при |g₁|>>|g₂|; g _eq =2g₁ g₂ –1. При |g₂|>>|g₁| получаем аналогичную формулу с заменой индексов 1↔2.

С использованием выражений (1), (2) в настоящей работе получена интерполяционная формула для расчета дифракционных потерь мод ТЕМ00 и ТЕМ01 в резонаторах произвольной конфигурации, согласующаяся с известными частными случаями и удовлетворяющая законам подобия резонаторов:

AN g 1 , g 2 ) =

= <

A^S(N,g m ) + (^-^ g_m

) k [ A^h(N,g m ) — A^S(N,g m ) ]

g M ^ 1

d N          1

A ⁽~   , ^g eq ) ⁺ Г

2 g_M      g_M

/            л N

A^h(N,g m ) - A d (N

2 g m — 1 ) ,g M >  1

где g_m= min {| g ₁|,| g ₂|}; g_M= max {| g ₁|,| g ₂|}.

Показатель степени k должен обеспечивать непрерывную дифференцируемость функции Λ в области устойчивости резонатора и приближенно равен 1,5. Эта формула дает точные значения потерь для симметричного и плоскосферического резонаторов, удовлетворяет законам подобия и при |g₁|>>| g ₂| или | g ₂|>>| g ₁| асимптотически описывает потери в соответствии с выражением (2). На рис. 1б для иллюстрации приведена рассчитанная по формулам (1), (3) зависимость дифракционных потерь от g ₁ и g ₂ в области 0 ≤ g ₁ g ₂ ≤ 1, g ₂ ≥ g ₁ ≥ 0 . Численное решение интегральных уравнений Ли для ряда конфигураций резонаторов при различных числах Френеля позволяет оценить точность интерполяционной формулы в 5 % [10].

ПОТЕРИ В МНОГОЭЛЕМЕНТНОМ РЕЗОНАТОРЕ

Формулу (3) можно обобщить на случай сложного резонатора с произвольным числом гауссовых элементов, расположенных между двумя диаф р агмированными зеркалами с диаметрами 2 a ₁ и 2 a ₂ соответственно. Пусть А ₀, B 0 , C 0 , D 0 - элементы матрицы передачи набора оптических элементов, включая активную среду с квадратичным распределением в радиальном

направлении показателя преломления и коэффициента усиления, расположенных между зеркалами 1 и 2 с радиусами кривизны R ₁ и R ₂ соответственно. Тогда, произведя в интегральном преобразовании Кирхгофа в приближении Френеля [2] замену переменных x=r ₁ /a ₁, y=r ₂ /a ₂, φ ₁ (x)=a ₁ Y ₁ (r ₁ ) , φ ₂ (y)=a ₂ Y ₂ (r ₂ ) , получим систему интегральных уравнений:

У 1 Ф 2 ( У ) = J L 1 ( У , x ) Ф 1 ( x ) xdx , 0

Y 2 Ф 1 ⁽ x ) = J L 2 ⁽ x, У ) Ф 2 ⁽ У ) xdy, 0

случае формулой (3) можно пользоваться только когда длина капилляра L_a близка к длине резонатора L . Реально торцы разрядного капилляра, играющие роль диафрагм, находятся на некотором, часто значительном расстоянии от зеркал. Ясно, что для расчета потерь в этом случае необходимо решить систему четырех связанных интегральных уравнений типа (4). Именно не-учет этого фактора в [17] делает ее результаты ошибочными. В данной работе для резонатора с капилляром был использован другой подход.

Для оценки потерь используем эквивалентное число Френеля и параметры устойчивости резонатора [15]:

где Y _l, Y ₂ – радиальные распределения комплексных амплитуд пучка перед зеркалами 1 и 2; Л 1 = 1 - P i|2 ” Л 2 = 1 — p ₂| — потери мощности при отражении от диафрагмированных зеркал; ядра уравнений L ₁ и L ₂ определяются формулой: L ₁ (y,x)=L ₂ (x,y)=i^{l+ 1} 2πNJ _l (2πNxy)exp{-iπN(G ₁ x 1² +G ₂ y ² )}, а N=a ₁ a ₂ /λB; G ₁ =a ₁ A/a ₂ , G ₂ =a ₂ D/a ₁ – параметры подобия резонатора; B=B ₀, A = A ₀ – B ₀/ R ₁, D = D ₀ – B ₀/ R ₂ – элементы матрицы передачи оптической системы, заключенной между диафрагмами 1 и 2.

Поскольку уравнения (4) совпадают с соответствующими уравнениями для «пустого» резонатора с параметрами: N=a ²/ λL , g ₁, g ₂, то для расчета эффективных потерь на проход в сложном резонаторе нужно использовать выражение (3), произведя замену a ²/ λL → a ₁ a ₂ / λB , g ₁→ G ₁, g ₂→ G ₂. Связь потерь на обход резонатора и эффективных потерь на проход дается выражениями:

Л , - 1 -1 ,, ,|’ - Л + Л , - ЛД. Л - 1 - ^. (5)

Рассмотренный случай расчета дифракционных потерь имеет практическое значение для сложных резонаторов, в которых селекция поперечных мод осуществляется с использованием диафрагмы, помещенной вблизи одного из зеркал, там, где диаметр пучка больше. В открытых резонаторах с диафрагмами или капилляром, торцы которого играют роль диафрагм, интегральное преобразование Френеля необходимо использовать столько раз, сколько пучок проходит через диафрагмы при полном обходе резонатора. Из условия самовоспроизводства поля при замкнутом цикле можно получить систему интегральных уравнений, позволяющих рассчитывать распределение амплитуды и фазы поля в выбранном сечении и определять дифракционные потери.

aa

N = -¹ 2

eq X L

aa

^G1 = 1 g g 1 , ^G 2 = T g 2

a ₂

a ₁

,

где λ – длина волны излучения; а_i=(w_ia)/ w_кi – эффективный радиус i -й диафрагмы; а – радиус капилляра; w_i , w_кi – радиусы пучка излучения на i-м зеркале и на ближайшем к нему торце капилляра. Проводя расчеты w_i и w_кi по «пустому» резонатору с неограниченными зеркалами [14], для эквивалентных параметров (6) получаем:

N = N eq

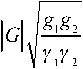
G i = g 1

g 2 Y 2 g i Y 1

gt Yx

G 2= 4 77" ,(7)

g 2 i 2

где G = g ₁ + g ₂ – 2 g ₁ g ₂ ; γ_i = β + [(1 – g_i ) g_j – ^Li G]²;

L

β = g ₁ g ₂(1- g ₁ g ₂); L_i – расстояние от i -го зеркала до торца капилляра; N = а ² /λL .

Расчет дифракционных потерь производится по формуле (3) с заменой N , g ₁, g ₂ на эквивалентные параметры согласно (7).

Выбор эквивалентных параметров в форме (7) продиктован, помимо соображений работы [15], необходимостью согласования наших результатов с предельным случаем короткого капилляра ( L_a →0) или резонатора с диафрагмой. Резонатор с внутренней диафрагмой эквивалентен двухзеркальному резонатору с ограниченными зеркалами при нескольких положениях диафрагм [1]. Так, при L 1 / L =(1+ V g 1 1 g 2 )^-1 для эквивалентных параметров из формул (7) получаем:

^Nq - ^N g^(^{( 1 +}6 ^{)( 1 +} g ’ g"*) ", G 1 = ^G ■ ■ ^ gg ² •

что точно соответствует результатам [1]. При

ПОТЕРИ В РЕЗОНАТОРЕ С КАПИЛЛЯРОМ

В большинстве случаев для газоразрядных лазеров используют резонатор, в котором лазерное излучение ограничено не краями зеркал или диафрагмой, а разрядным капилляром. В этом

этом дифракционные потери, согласно (3), равны Л=Л^s ( Neq, ^8 1 1^g 2 ). Для конфокального резонатора (g 1 =g₂=0), учитывая, что 48 1 18 2 = ( L-L j )/ L , из этой формулы получаем точное выражение

дифракционных потерь при любом положении

диафрагмы:

Л = Л(--NL ---,

2L 2 (L - L i )

0 ).

ГЕНЕРАЦИЯ МНОГИХ ПОПЕРЕЧНЫХ МОД

Значение дифракционных потерь основной и первой поперечных мод достаточно для целей расчета мощности основной моды и определения границы одномодовой генерации. При многомодовой генерации для определения распределения мощности по модам необходимо знание дифракционных потерь высших мод. Для дифракционных потерь TEM _pl- моды, используя метод эквивалентного конфок ^p ального резонатора [6], получаем:

кального коэффициента усиления в точке ( z , r , φ ) на приведенной частоте x при генерации многих

аксиальных и нескольких поперечных мод, используя (10) и выражение I = W | ^ | , имеем: _p,l pl pl

g ( x , z , r , ф ) =

_g ( z r ) e - x ²

^{1 +}E ^wpi ^{( x} V pi ^{( z,r,} ф ) ² / I o ⁽ z , r ) ’ p , l

2 п ( 8 nN ) 2 p + l -1      г ,

Л = —' , eq*  exp { - 4 nN } ,          ⁽⁸⁾

pl        p!(p +1)!                   eq где Neq = N^ 1 - g 1 g2 - эквивалентное число Френеля. Точность расчета по формуле (8) повышается при конфигурациях резонатора, близких к конфокальным (g1=g2=0), а также при N →∞. Используя (8), выразим потери Λpl через потери основной Λ и первой Λ -мод. Получим выражение:      00              01

где среда предполагается аксиально симметричной, а ψ _pl – нормированная комплексная амплитуда пучка; W_pl ( x ) – спектральная плотность мощности внутри резонаторного излучения TEM _pl -моды на частоте x. Суммирование ведется по всем генерирующим модам.

Систем а уравнений для рас чета W_pl (x) с учетом выражения (11) имеет вид: ^p

2 La    2n     a e -x J dZ J dф J

g 0 Ψ pl rdr

1 + E W mn ( X ) ^ mn | / I o

= L a KL , (12)

m , n

Л pl

Л

/ Л

—01

2 p + l \

\

Л

0 0 J

,

которым можно пользоваться для определения потерь высших мод. При Л _р >  1 необходимо положить Л pl = 1 .

Знание дифракционных потерь высших мод Λ и позволяет определить, сколько и какие моды генерируют и их распределение по мощности. Метод расчета основан на моделировании процесса развития генерации, начиная с основной или первой моды. Рассмотрим суть метода на примере лазера с квазиоднородным уширением линии генерации, когда в пределы контура усиления попадает несколько собственных частот резонатора ν _q , для которых межчастотный интервал с/2L сравним с лоренцевской шириной линии.

Коэффициент усиления для прямой и обратной волн излучения генерации на приведенной частоте x =(ν–ν ₀ )/Δν ₀ , где Δν ₀ = Δν _D /2 _{ln 2} ; Δν_D – доплеровская ширина линии, имеет вид:

g ■ ( * ) -

g 0 e

¹ + I ( x ) / I 0

где g ₀ , I ₀ – ненасыщенный коэффициент усиления для центра линии и интенсивность насыщения; I(x) – спектральная плотность интенсивности внутрирезонаторного излучения. Рассмотрим открытый резонатор с активной средой, заключенный в цилиндрический разрядный капилляр радиуса a и длиной L_a . Используя цилиндрическую систему координат для ло-

где K _l ^p _o ^l _ss – коэффициент потерь TEM _pl -моды. Число уравнений (12) равно числу генерирующих мод. Физический смысл этих уравнений заключается в равенстве потерь моды TEM _pl среднему по объему активной среды, насыщенн ^p ому всеми остальными генерирующими модами коэффициенту усиления для рассматриваемой моды. Расчет прекращается, когда выполняется неравенство:

La ² ? a г I¹/⁷ l²r

¹                   g о К m + 1 ^rdr         m + 1 +1

т J ^dz J ^{а ф} J   г м——; <  K oss , ⁽¹³⁾

La 0 0   0 1 + 1 J Wy (0) ^/ о j-1

выражающее тот факт, ч то насыщенный генерирующими модами коэффициент усиления для M +1-моды меньше потерь для нее. Здесь для простоты двойную индексацию мод ( pl ) заменили одинарной ( i ) в соответствии с ростом дифракционных потерь.

Система уравнений (12) позволяет рассчитывать частотную зависимость Wpl(x) и распределение мощности Wpl по модам: p xpl

W pl = ² J W pl ( ^x ) dx ,               ⁽¹⁴⁾

где x_pl – значение приведенной частоты, при которой W_pl(x)=0.

На рис. 2 изображены рассчитанные зависимости нормированных мощностей N_pl = W _pl /( ^ w ² 1 0 ) от числа Френеля резонатора N и параметра конфигурации g для симметричного изотропного резонатора с диафрагмами на зеркалах при g ₀ =10-2см-1, λ =0,483 мкм, g₀( r ) = = 1,47 g ₀ [1 – 0,21( r / a )² – 0,65( r/a )⁴]; L_a =20 см, K₀=10^-3 см^-1 – коэффициент потерь без учета дифракционных.

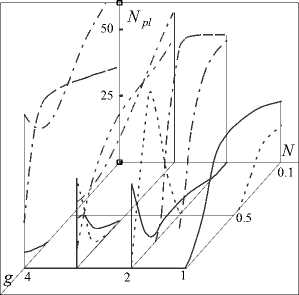
Рис. 2. Зависимость нормированной выходной мощности N _pl от числа Френеля N и параметра устойчивости g для симметричного резонатора: ^___ – N ₀₀ , - - – N ₀₁ , -• – N ₁₀ ,

-.. -.. – высшие моды ( N ₁₁ +N ₂₀ )

Данные этого рисунка представляют общие закономерности распределения мощности по модам. Видно, что число генерирующих мод увеличивается с ростом N и уменьшается с ростом g. Наблюдаемые закономерности обусловлены изменением дифракционных потерь.

ОДНОМОДОВАЯ ГЕНЕРАЦИЯ

Критерием одномодовой генерации является условие:

г а ф г    g ol * 0.12 rd

0    0 1 + 7 W  (0)| * ool

I ₀

- <  K 01

₂ loss ,

где W ₀₀ ( 0 ) - спектральная плотность мощности основной моды для центра линии. Это неравенство так же, как и (13), отражает факт превышения потерь моды TEM₀₁ над насыщенным излучением основной моды коэффициентом усиления первой моды и, следовательно, невозможность ее генерации.

На рис. 3а представлены зависимости g0(r)/g ₀ ( 0 ) для двух случаев радиальной зависимости ненасыщенного коэффициента усиления. Первый характерен для ионных лазеров, работающих при малых токах, а второй – при больших токах и давлениях. Наблюдаемый на радиальной зависимости g ₀ (r)/g 0 ( 0 ) провал связан с ростом влияния девозбуждения верхнего лазерного уровня электронным ударом и с пленением резонансного излучения с нижних лазерных уровней.

На рис. 3б представлена диаграмма, полученная при обработке результатов расчета по описанной выше методике. По осям отложены параметры X оо - gT/ K1 и X 01 - g 01 / ^KL ^- превышения усредненных коэффициентов усиления для мод TEM₀₀, TEM₀₁ над коэффициентами потерь. Сплошные и штриховые линии соответствуют двум случаям радиального распределения коэффициента усиления. Точки, лежащие ниже кривых (1), соответствуют генерации моды TEM₀₀.

Цифры на кривой 1 пропорциональны мощно-

сти. Так, для точки A ( X =4, X ₀₁=2), N - W (™² I 0 ) = 7,9.

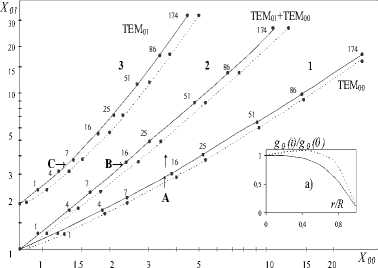
Рис 3. Поперечное распределение ненасыщенного коэффициента усиления (а) и диаграмма, описывающая двухмодовую генерацию (б)

Кривые 2 и 3 построены для случая изотропного резонатора и резонатора с анизотропными элементами, например окнами Брюстера. В области выше кривой 2 (3) генерирует только мода TEM₀₁. Мощность при этом определяется аналогично случаю моды TEM₀₀, так как для точки В ( X ₀₀=2, X₀₁=3,6) в изотропном резонаторе N ₀₁ - 7,9, а для точки С ( X ₀₀=1,2, X₀₁=3,6) в анизотропном резонаторе N 01 - 3,1. Как и следовало ожидать, мощность TEM₀₁-моды в анизотропном резонаторе при одинаковых значениях X ₀₁ ниже, чем в изотропном, что связано с меньшим, чем в первом случае, объемом активной среды, с которым взаимодействует мода. В области между кривыми 1 и 2 (1 и 3) реализуется двухмодовая генерация.

Результаты, представленные на рис. 3, приведены для случая a / w = 2. Фактически для a / w >  1,7 они не чувствительны к отношению a / w , что и делает диаграмму универсальной. Режимы, соответствующие точкам B и C , реализуются в случае провала радиальной зависимости коэффициента усиления, а также вследствие выгорания части зеркала или загрязнения оптических элементов, когда X ₀₁ может превысить X ₀₀ и возможна устойчивая генерация моды TEM₀₁.

ЗАВИСИМОСТЬ МОЩНОСТИ

ОТ РАЗЪЮСТИРОВКИ

Подход к расчету дифракционных потерь в резонаторе с капилляром, развитый выше, в силу его искусственного характера требует дальнейшего обоснования. Такое обоснование легче всего получить, сравнивая результаты его применения с экспериментальными данными, полученными при разъюстировке зеркал резонатора. При разъюстировке оптическая ось вну-трирезонаторного излучения смещается относительно оси капилляра, что ведет к уходу оси диаграммы направленности излучения и к росту дифракционных потерь. Смещение оси пучка в плоскости торцов капилляра в практически важных случаях поворота зеркал в одной плоскости на углы δ1 и δ2 описывается выражениями, следующими из геометрических соображений:

S i k =

1 - g ₁ g ₂

$ ₂ k = ——

¹ - g 1 g 2

L 1

g 2 ⁺ 1 ^{( 1} - g 2 ) ⁵ 1 + ¹ - 1 ( ( 1 - g 1 ) ⁵ 2 L

2 L 2 ⎦ 1 ⎢⎣ L 1 ⎥⎦ 2 ⎭

^ ^{( 1} - g 2 ) ⁵   1

L

-

L ^{( 1} - g 1 ) ] ⁵ 2 I .

λ = 488 нм [18]. Параметры лазера, использованные при расчете: L = 660 мм, L ₁= L ₂= 230 мм, диаметр разрядного капилляра 2 а = 3 мм, зеркала – R ₁= ∞ , R ₂= 2 м, коэффициенты отражения зеркал ρ ₁= 0,95, ρ ₂ ≅ 1, характер уширения линии – ква-зиоднородный. В съюстированном лазере генерирует мода TEM₀₁ вследствие провала коэффициента усиления в центральной части активной среды. При разъюстировке начинает генерировать мода TEM₀₀, обладающая меньшими дифракционными потерями.

Согласно [18] разъюстированный симметричный резонатор с диафрагмами на зеркалах эквивалентен некоторому съюстированному резонатору с ассиметрично расположенными диафрагмами. Такой резонатор при S _{1 k}= S _{2 k} = S описывается двумя числами Френеля N ^± = N (1± S/a )², а потери определяются по формуле:

Л = 0,5[л (N +)+A (N -)].

В нашем случае при S _{1 k} ≠ S _{2 k} будем описывать разъюстированный резонатор четырьмя числами Френеля N ^±_1,2 = N _э(1 ± S_{1,2 k} / а)², а потери по аналогии с симметричным резонатором определять по формуле:

Л ( 5 1 , 5 2 ) = 0,25 [ л ( ^ ₁ ⁺) + л ( N ^-) + л ( N ₂ ⁺) + л ( N - )] . (17)

Коэффициент потерь в разъюстированном резонаторе связан с дифракционными потерями на проход соотношением:

K, = K + K/ ^ , & ) = K +— In ----¹----.(18)

loss ^{0      1 1 2        0} La 1 - Л ( & 1 , 6 2 ) ^V ’

Здесь K₁ определяет дифракционные потери; K₀ характеризует все остальные виды потерь, включая полезные.

На рис. 4 представлены рассчитанные зависимости потерь Λ ( δ ,0), Λ (0, δ ) и относительных выходных мощностей в сравнении с экспериментальными данными, полученными при генерации моды ТЕМ₀₁ лазера на длине волны

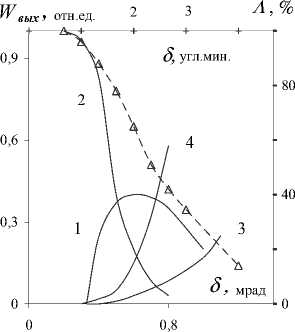
Рис. 4. Рассчитанные зависимости выходной мощности для мод ТЕМ00 (1) и ТЕМ01 (2) и дифракционных потерь (3, 4) от угла поворота выходного зеркала для ArII-лазера в сравнении с экспериментальными данными (∆)

ЗАКЛЮЧЕНИЕ

Предложенный в работе подход позволяет рассчитывать дифракционные потери основной и высших поперечных мод в сложных многоэлементных резонаторах, распределение поперечных мод по мощности и границу одномодовой генерации, определять такие характеристики выходного пучка, как его диаметр и расходимость при заданной конфигурации резонатора, зависимость выходной мощности от разъюстировки зеркал резонатора. Описанный метод можно эффективно использовать при создании лазеров.

* Работа выполнена при поддержке Программы стратегического развития ПетрГУ в рамках реализации комплекса мероприятий по развитию научно-исследовательской деятельности на 2012–2016 гг.

Mol’kov S. I., Petrozavodsk State University (Petrozavodsk, Russian Federation)

DIFFRACTION LOSSES AND POWER DISTRIBUTION

IN A GAS-DISCHARGE LASER OVER TRANSVERSE MODES

REFERENCIS

• 1.    Av e rb a k h V. S . , V l a s o v S . N . , Ta l a n o v V. I . Open Resonators with Randomly Located Diaphragm [Otkrytye rezonatory s proizvol’no raspolozhennoy diafragmoy]. Zhurnal tekhnicheskoy fiziki [Journal of Technical Physics]. 1966. Vol. 34. № 3. P. 497–507.

• 2.    Born M., Wol’f E. Osnovy optiki [Fundamentals of Optics]. Moscow, Nauka Publ., 1973. 720 p.

• 3.    Gromov A. N., Trashkeev S. I. Simple Formulas for Calculation of Losses in Symmetric Stable Resonators from Round Mirrors [Prostye formuly dlya rascheta poter’ v simmetrichnykh ustoychivykh rezonatorakh iz kruglykh zerkal]. Optika i spektrosкopiya [Optics and Spectroscopy]. 1987. Vol. 2. №. 3. P. 618.

• 4.    Doronin V. G., Novikov V. I., Pipchenko V. P., Stepanov V. A. Influence of the Active Medium Inhomogeneity and Diaphragms on Parameters of the CO2-Laser’s Output Beam [Vliyanie neodnorodnosti aktivnoy sredy i diafragmy na parametry vykhodnogo puchka odnomodovogo СO2-lazera]. Kvantovaya elektronika [Quant. Electron]. 1982. Vol. 9. №. 5. P. 876–883.

• 5.    D o r o n i n V. G . , P i p c h e n k o V. P . Off-axis Gaussian Beams for Describing the Radiation of Lasers with a Misaligned Active Resonator [Vneosevye gaussovy puchki dlya opisaniya izlucheniya lazerov s raz’’yustirovannymi aktivnymi rezonatorami]. Zhurnal prikladnoy spektroskopii [Journal of Applied Spectroscopy]. 1981. Vol. 35. № 1. P. 9–16.

• 6.    Ishchenko E. F. Otkrytye opticheskie rezonatory [Open Optical Resonators]. Мoscow, Sovetskoe radio Publ., 1980.

• 7.    Ko r z h av i n V. A . , O r e s h a k O . N . , S am o r o d o v V. G . , S h i r ob ak i n S . E . Influence of Misalignment on Power Output of the Ionic Argon Laser [Vliyanie raz’’yustirovki na vykhodnuyu moshchnost’ ionnogo argonovogo lazera]. Elektronnaya tekhnika [Electronic Technic]. 1985. Ser. 11. № 1. P. 54–59.

• 8.    Kub a r e v V. V. Babinet Principle and Diffraction Losses in Laser Resonators [Printsip Babine i difraktsionnye poteri v lazernykh rezonatorakh]. Kvantovaya elektronika [Quant. Electron]. 2000. Vol. 30. № 9. P. 824–826.

• 9.    K u b a r e v V . V. Calculation, Optimisation, and Measurements of Optical Resonator Parameters of the Novosibirsk Terahertz Free-electron Laser [Raschet, optimizatsiya i izmerenie parametrov opticheskogo rezonatora Novosibirskogo teragertsovogo lazera na svobodnykh elektronakh]. Kvantovaya elektronika [Quant. Electron]. 2009. Vol. 39. № 3. P. 235–240.

• 10.    M o l ’ ko v S . I . Diffraction Losses and Distribution of Power of Gas-discharge Lasers on Transverse Modes [Difraktsionnye poteri i raspredelenie moshchnosti gazorazryadnykh lazerov po poperechnym modam]. Sbornik dokladov 19-y mezhdunarodnoy konferentsii “Lazery. Izmereniya. Informatsiya” [Proceedings of the 19 – th International Conference “Lasers. Measurements. Information”]. St. Petersburg, Publishing SPPU, 2009. Vol. 1. P. 22–35.

• 11.    Mol’kov S. I., Stepanov V. A. Calculation of Output Characteristics of the Ionic Lasers on Inert Gases [Raschet vy khodnykh kharakteristik ionnykh lazerov na inertnykh gazakh]. Vestnik Ryazanskogo pedagogicheskogo universiteta [Vestnic of the Ryazan Pedagogical University]. 1994. № 1. P. 57–67.

• 12.    B o y d G . D . , G o r d o n J . P. Confocal Multimode Resonator for Millimeter Through Optical Wavelength Masers // Bell Syst. Tech. J. 1961. Vol. 40. P. 489–508.

• 13.    C a s p e r s o n L W. , L u n n a m S . D . Gaussian Modes in High Loss Laser Resonators // Appl. Optics. 1975. Vol. 14. № 5. P. 1193–1199.

• 14.    Ko g e l n i k H . W. , L i T . Laser Beams and Resonators // Appl. Opt. 1966. Vol. 5. P. 1550–1567.

• 15.    Kogelnik H. W. Imaging of Optical Modes Resonators with Internal Laser // Bell. Syst. Tech. J. 1965. Vol. 44. № 3. P. 455–494.

• 16.    L i T . Diffraction Loss and Selection of Modes in Maser Resonators with Circular Mirrors // Bell. Syst. Tech. J. 1965. Vol. 44. № 5. P. 917–932.

• 17.    R i g r o d W. W. Diffraction Loss of Stable Optical Resonator s with Internal Limiting Apertures // IEEE J. Quant. Electron. 1983. Vol. 19. № 11. P. 1679–1685.

• 18.    S a n d e r s o n R . , S t r e i fe r W. Laser Resonators with Tilted Reflectors // Appl. Opt. 1969. Vol. 8. № 11. P. 2241–2250.