Дифракционный датчик волнового фронта

Шака-Гартмана. Размеры отверстий определяют точность и пространственное разрешение данного датчика [2]. Однако, уменьшение апертуры отверстий приводит к увеличению дифракционной расходимости пучков, что ограничивает возможности такого подхода.

В настоящей работе анализируется возможность использования датчика волнового фронта, основанного на явлении дифракции и эффекте Тальбота [3]. С точки зрения пространственного разрешения и стоимости системы такой датчик волнового фронта имеет ряд преимуществ по сравнению с описанными выше. Для получения упорядоченной структуры пятен на приёмнике предлагается использовать дифракцию на двумерной периодической структуре [4].

Выберем направление оси Z вдоль оптической оси системы. Пусть плоскость X0Y0 совпадает с положением решетки. Тогда комплексную амплитуду сферической волны, падающей на решетку в параболическом приближении можно записать как:

i n x o+ y o)

и ( x 0 , У o ) = U 0 e “ , ⁽¹⁾ где R – радиус сферического волнового фронта, λ – длина волны.

Пропускание периодической структуры (решетки) можно представить в виде произведения двух рядов Фурье, соответственно по оси xо и yо, от 2 innx0 от 2 inmy 0

t(x0, У0) =Е Ane d X Ame d , (2) n=-∞ m=-∞ где d – период решетки, а Am, An – коэффициенты разложения.

Если поперечные размеры решеток достаточно велики для того, чтобы можно было пренебречь краевыми эффектами, то комплексную амплитуду поля в плоскости наблюдения ( x₁,y₁ ), отстоящей от решетки на расстояние z₁ , можно описать с помощью дифракционного интеграла Френеля:

2 inz, ; to to e A

U ⁽ X , У 1 ) =— I J U ⁽ x o , У о ) ' t ⁽ x o , У о ) ' exp ^{i A z} i -to-to

^П ( ( x - x ) 2 + ( y , - У о ) 2 ) dxdv Az, '                           '

В результате аналитических преобразований получим

U ⁽ x i , У 1 ) =

2 i n z , ^{n ( x} 2 ⁺ У i^{2 )} e ^a e ^A (R ⁺ z ) и 0

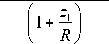
to

' E Am exP m=-to

E ^to ,     ( i nA n ² Rz. |    ( 2 i n nRx,

A exp ¹ exp ¹

n =_      ^P( d ² ( z 1 + R ) J      d ( z i + R )

i nA m ² Rz i d ² ( z , + R )

exp

2 i п mRy 1 | d ( z i + R ) J

Откуда видно, что в случае плоского волнового фронта (R ^ to) при выполнении условия exp

i nA ( n ² + m ² ) z_x

d ² к

= i .

распределение поля с точностью до несущественного фазового множителя совпадает с функцией пропускания решетки (2). В этом собственно и заключается эффект Тальбота. Нетрудно заметить, что условие (4) выполняется если расстояние z ₁ кратно некоторому периоду

2 d ²

zT =----

T A

.

Для анализа полученного выражения (3) удобно перейти к безразмерным параметрам. Для этого нормируем поперечные координаты на период решетки d , а продольную координату на zT x1

d

У = ^Уа , d

z = ^

zT

Введем понятие нормированной кривизны волнового фронта H =   .

R

Тогда, пренебрегая не влияющими на интенсивность фазовыми множителями, получим:

U ⁽ x , У) =

U 0

( i + Hz )

2 inn ² z 2 innx to

E Ae ^{( i +} Hz ) e ^{( i +} Hz )

n =—to

2 inm ² z 2 inrntv to         -------- -----

■ E A me - H ) e - H )

m =-to

При отличной от нуля кривизне H изменение поперечного масштаба в соответствии множителем -—i^— описывается радиальной проекцией исходного распределения поля за решеткой на плоскость наблюдения. При этом точкой, из которой производится проекция является центр кривизны волнового фронта. Таким образом, в первом приближении поперечное смещение пятен происходит в соответствии с законами геометрической оптики. Иными словами, зависимость смещения световых пятен образующихся в за счет дифракции в такой схеме от локального наклона волнового фронта будет аналогична соответствующей зависимости для гартмановского датчика. Однако сами размеры пятен и расстояния между ними можно существенно уменьшить, так как в данной схеме явление дифракции не размывает световые пятна, а наоборот формирует структуру распределения интенсивности в виде отдельных пятен. Поэтому в подобном дифракционном датчике можно получить большую точность и пространственное разрешение по сравнению с датчиком гартмановского типа.

При увеличении кривизны волнового фронта как в датчике Шака-Гартмана, так и в дифракционном датчике кроме смещения пятен происходит их размытие (увеличение размеров), что, в конечном счете, ограничивает верхний предел измерения кривизны волнового фронта. Однако в отличие от гартмановского датчика, где размытие пятен происходит за счет дефокусировки и внеосевых аберраций, в дифракционном датчике искажения формы пятна при увеличении кривизны волнового фронта носят более сложный характер. Для детального анализа данной ситуации необходимо конкретизировать функцию пропускания дифракционной решетки t ( x , y ) .

С технической точки зрения, наиболее просто реализовать подобного типа датчики с помощью бинарной решетки, то есть решетки состоящей из прозрачных и непрозрачных участков. Такая решетка описывается двумя параметрами: периодом d и отношением 5 = d/b периода к ширине прозрачного участка b , которое в соответствии с терминологией, принятой для описания импульсных сигналов, далее будем называть скважностью.

Основным параметром, определяющим метрологические характеристики дифракционного датчика, является период решетки d , поскольку для заданной длины волны он определяет z_T , т.е. базу на которой происходит смещение световых пятен. Вместе с тем, на точность измерения влияет и значение скважности s . Т.к. точность определения положения пятна зависит от его размеров, то уменьшение ширины пятна позволяет повысить точность измерения его смешения при том же размере базы. Из этих соображений следует, что для повышения точности измерений нужно увеличивать скважность.

Однако эта ситуация не столь однозначна. Здесь нужно учесть, что при увеличении кривизны измеряемого волнового фронта размытие световых пятен, соответствующих большему значению s , происходит быстрее. На рис.1 показано изменение пространственного распределения энергии светового пятна в зависимость от отно-

а.

п ы

г.

в.

б.

д.

е.

Рис.1. Распределения интенсивности в пределах пятна а – s=2, H=0 ; б – s=7, H=0; в – s=2, H=0,015; г– s=7, H=0,015; д – s=2, H=0,03 ; е - s=7, H=0,03

сительной кривизны H для двух значений скважности s = 2 и s = 7.

Видно, что для малой скважности s при увеличении относительной кривизны H , несмотря на появление дифракционной структуры, световое пятно в целом сохраняет свою форму и размеры. Для большего же значения скважности ( s = 7) при увеличении H до 0,03 размер пятна настолько увеличивается, что оно становиться даже больше, чем пятно, соответствующее меньшему значению скважности.

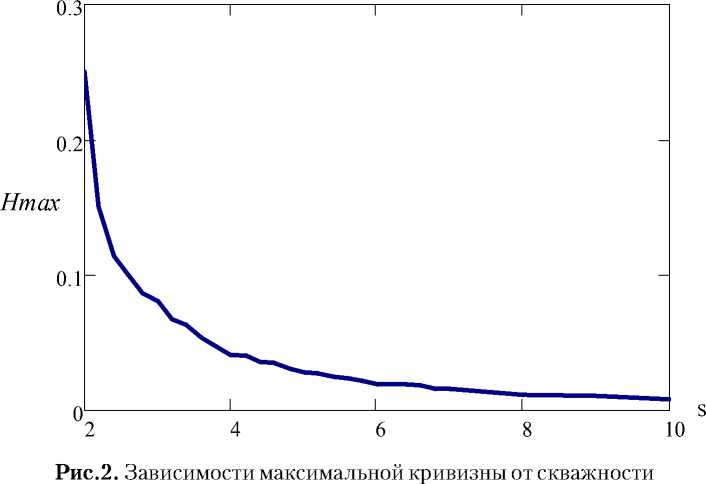
Для количественной оценки верхней границы регистрируемой кривизны волнового фронта необходимо ввести некоторый критерий размытия пятна. В нашей работе было предложено считать максимально возможным такое значение кривизны H, при котором в область, соответствующую идеальному (не размытому) пятну попадает половина энергии всего пятна. Были рассчитаны зависимости значения энергии, попадающей в область идеального пятна, от относительной кривизны для различных значений скважности. Опираясь на полученные данные, был построен график зависимость максимальной кривизны от скважности (рис. 2):

Из полученной зависимости видно, что попытки увеличить чувствительность за счет увеличения скважности, будут приводить к уменьшению верхней границы диапазона регистрируемой кривизны поля.

Таким образом, в работе был представлен новый тип датчика волнового фронта, основанный на эффекте Тальбота.

Для бинарной решетки было проведено численное моделирование искажения дифракционных пятен в зависимости от изменения кривизны волнового фронта. Проведены оценки чувствительности данного датчика.

Рассчитаны значения максимально регистрируемой кривизны волнового фронта для решеток характеризуемых различными значениями отношения периода к ширине прозрачной части.