Дифракционный расчет интенсивности светового поля вблизи фокальной линии

В работе [1] были приведены геометрооптические алгоритмы расчета фазовой функции фокусаторов в гладкие кривые, а в [2,3] проведен анализ их фокального поля с учетом дифракционных эффектов.

Составные фокальные области, сформированные из сегментов фокальных кривых, могут быть получены составными фокусаторами с кусочно непрерывной фазовой функцией. Метод расчета фокального светового поля от составного фокусатора, предложенный в данной работе, учитывает специфику дифракционного формирования каждого сегмента фокальной кривой и интерференционные эффекты в местах стыковки сегментов. При этом обобщен частично геометрооптический подход к вычислению дифракционных интегралов.

Рассмотрим задачу фокусировки пучка когерентного света с длиной волны X и комплексной амплитудой w_q(u, v) в составную фокальную область, представляющую объединение сегментов гладких кривых L

L = и L , ( 1) J=i J каждая из которых имеет длину 1^ и описывается параметрическими уравнени ями

( Х = Х/^> I у = W

0< ^<^,

£ - натуральный параметр на гладкой кривой Ljf

(х, у) - декартовые координаты в плоскости фокусировки,

(u, v) - декартовые координаты в плоскости фокусатора.

Световое отверстие G может быть реализовано в виде объединения G=U G^ непересекающихся областей G^, каждая из которых в геометрооптическом приближении обеспечивает фокусировку в гладкую кривую L^ соответственно. Поле w(x, у) в фокальной плоскости составного фокусатора G формируется путем интерференции парциальных фокальных полей w^x, у), создаваемых за счет дифракции падающего пучка wq(u, v) в областях G^ фокусатора ширину интео-

w( х, у) - £ Wj( х, у).

Распределение интенсивности I^x.y) = | w^ х, у) |2, определяющее каждого сегмента кривой L , исследовано в [2, 3]. Для исследования ференционных эффектов, описываемых формулой (3), примем во внимание фазу парциального поля w , вычисляемого, например, с помощью интеграла Кирхгофа [4] к                      г w/x.y) ” “2ЙП-- ' exP(ikf0} J wQ(u, V) X °                      G

Г -к f                                       J 1                         (4)

x exp (x-u)2 + (y-v)2 +ik 0 (u, v) + ф d2u, где wq( u, v) - комплексная амплитуда падающего пучка; k

• -г--ф ( u, v) - геометрооптическая фазовая функция фокусатора из о ^J         области С^ в сегмент кривой L^;

• ф - начальная фаза в области G ; oj                                                              j

• f       - фокусное расстояние; к - 2п/А.

о

Расчет фокального светового поля прямым вычислением интеграла Кирхгофа обладает значительной трудоемкостью как не учитывающий специфики задачи. Для упрощения общего интеграла (4) используем частично геометрооптический характер процесса фокусировки вдоль кривой Lj. А именно, будем считать, что парциальное поле Wj(х, у) во внутренней точке (х, у)еЬ^ формируется лишь той частью светового фокусируемого пучка, которая излучается из окрестности соответствующего слоя. Здесь аналогично [1,3] слоям, соответствующим точке (х, у)еЬу называется множество точек (u, v)€Gjt лучи ст которых сходятся в точку (х, у). В параксиальном приближении слои фокусатора представляют собой прямые, перпендикулярные касательной L^ в рассматриваемой точке (х, yleLy

Удобно ввести, как и в [3], специальную систему координат р - (а,/3), связанную со слоями в области G_jf так чтобы ось р совпадала с соответствующим слоем, а ось а была ему перпендикулярна:

u = (с(^) fo + хо(^)х^(€))х'(^) + (х'(£) х р), v = (c(^)fo + хо(^)хо(^))уо(^) + (х0(С) • 3),

• (•) - символ скалярного произведения;

• (х) - символ векторного умножения.

Вычисляя интеграл по переменной а методом стационарной фазы, получаем приближенное представление интеграла (4) в виде

/к *      (               г        r-ik7) р ч w/x.y) = /-^ • exp i(* + ф ) [dp-exp— f— w(p) ;

^xj " -^F" <^х2+У²> -t{(^c<6j>^£₀⁺

0                 0(6)

+ X X - X ) X + V 1 I 4 0     ( O^J^y0^^j^,yJj

• V ⁰

+ t; J xo [^(uft.o)) -^-Lat. %

/                            -1/2 И

• «W = «0 U(O.S), v(O,0) LL" (0.0)] xe'^; - W (0).

) I “        )kp

"       (               /--------------------------3(7)

^Wk_P^ Vn * ^Wo[^u(^s‘^⁾]/^_J (s, Pl-ф^О, 3) x

• x Р)а(0'^] • K,[/$ (* (s.0)-|6 (0,0))]= -

• a " Г1^^’ a ~ Г2(^)    - уравнения границ фокусатора в

переменных а и р.

(XXX

V^ а, £) = - xQ^

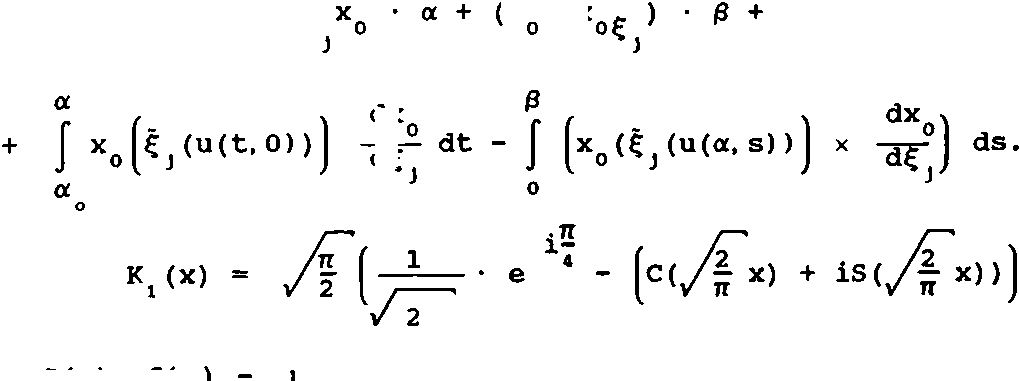
dx интегралы Френеля;

C(x)

где S(x),

- локальные координаты в окрестности сегмента кривой Ljt

связанные с координатами х и

У = y0J

X

XOJ

у фокальной области соотношениями te? - х0(^>^

(^) - У^Ш, .

В которых xo(€j)

дх (£ )

а значения х , у о ² о

L^ в окрестности

при ее

£,< [о. lj] граничных

продолжаются линейно за пределы точек. Член, содержащий функцию

кривой

К (х),

описывает эффекты, обусловленные конечностью апертуры. По сравнению с

результатами фазу поля в сегментов L

J

[2] формула (6) наряду с интенсивностью позволяет вычислить и

исследования интерференции

iki}

-1/2

-ikT) В фокальной области, необходимую для фокальных кривых.

VW = "^

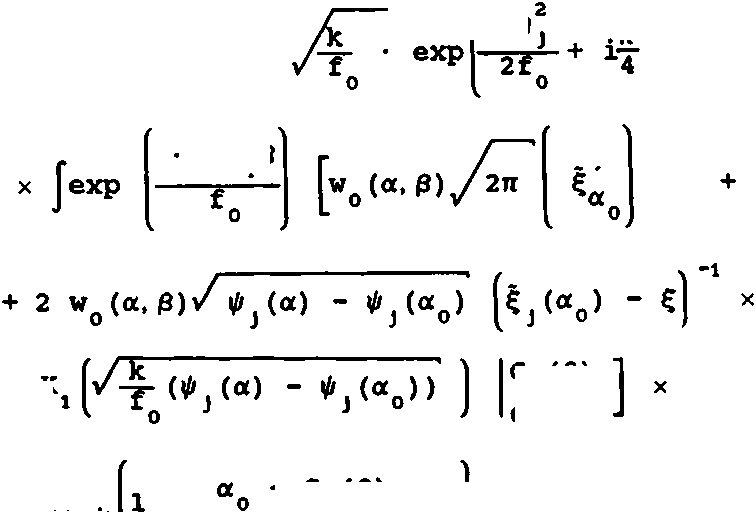
,п х К

X

J d/3.

х rect

GJB) G, (В)

- G2(p) G/3) - G2(p)

ао определяется из уравнения £ = £ (а ) между слоями области G фокусатора и отверстия.

(Ю)

, где ^(а) определяет соответствие соответствующими точками фокального

а tjr(«)

геометрооптическая фаза на отрезке.

В качестве примера применения полученных формул приведены расчеты распределения интенсивности в фокальной области фокусатора плоского пучка прямоугольного сечения размера b х Ь в контур квадрата размера 2а х 2а с параметрами X = 0, 6 мкм, fQ= 300 мм, 2а = 20 мм, 2Ь = 12,8 мм. Из рис. 1 и 2 видно, что интерференция в точках стыковки - вершинах квадрата - приводит к усилению осцилляций и уширению фокальной линии вблизи вершины.

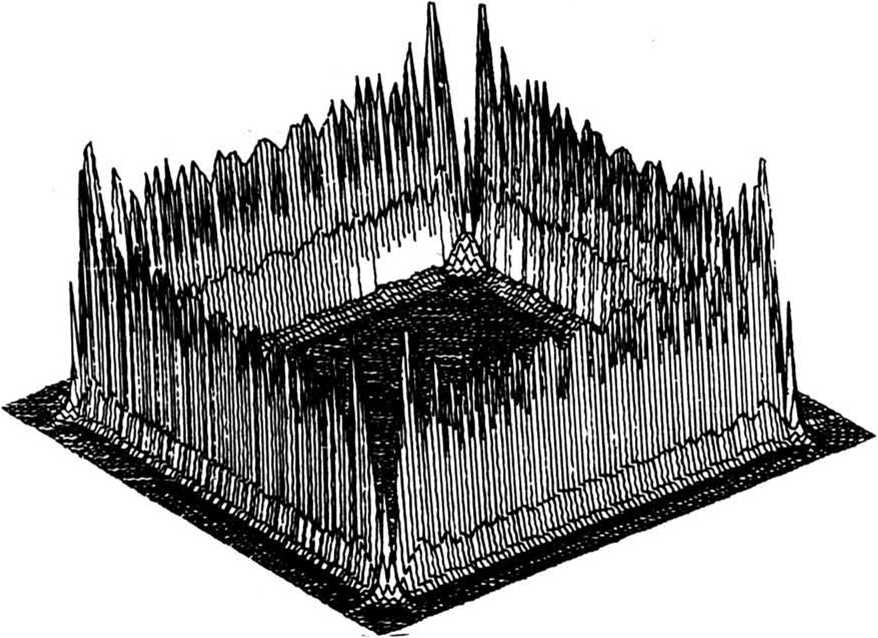
Рис. 1. Трехмерный график распределения интенсивности в фокальной области фокусатора в контур квадрата

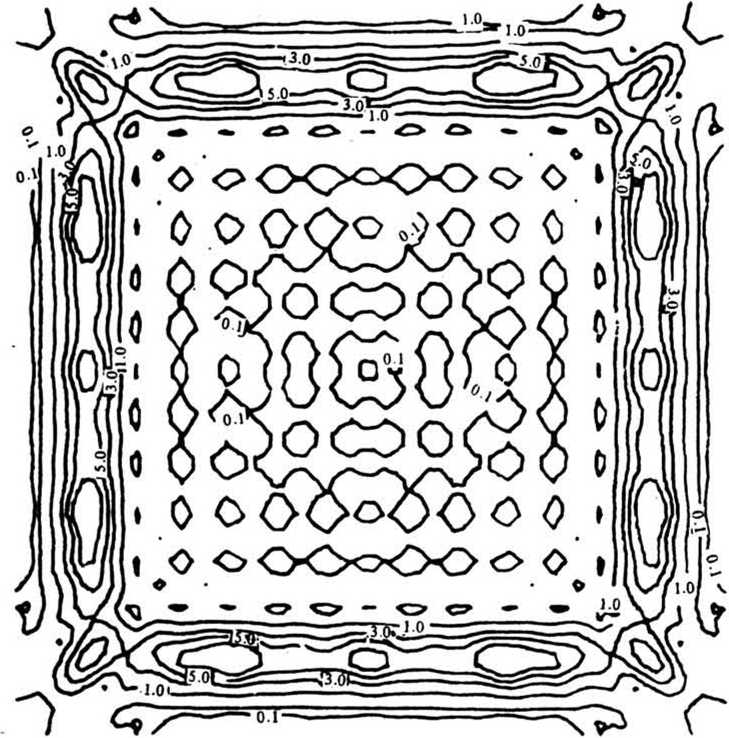
Рис. 2. Изофоты в фокальной области фокусатора в контур квадрата

Расчеты по формуле (6) позволяют найти ширину А фокальной линии по уровню е.

I (хд - А, у) - I (х0,у),                      (И)

а также энергетическую эффективность фокусатора

J I(x) d2x

Ad где Е — J|wo(u)|2d2u - световой поток, падающий на фокусатор;

AD - расширение контура квадрата, т.е. множество точек (х, у), отстоящих от контура на расстоянии не более А/2.

В таблице показана зависимость энергетической эффективности т) от параметра х ■ b-а *

где b - размер фокусатора.

Из анализа результатов, приведенных в таблице, видно, что энергетическая эффективность 7) падает при приближении размеров контура к дифракционному пределу.

Зависимость энергетической интенсивности от параметра к

к	0,2	0,1	1 15	1 20	1 50	1 100	1 200
1?	74,7	83,2	83,5	84,5	86,8	87,9	88,7