Digital Image Scrambling Based on Two Dimensional Cellular Automata

Cellular Automata (CA) are discrete models studied in computer science, mathematics, physics, computability theory, complexity science, theoretical biology and microstructure modeling. This basic theory of the classical CA was established by Von Neumann [1]. Later, Stephen Wolfran developed the theory [2]. CA can simulate abundant and complicated process of evaluation and can be considered as a dynamics system whose dimension is infinite. CA models is more than an important model of computer theory and it is applied in the study of non-linear appearance and fractal structure in mathematics, physics, biology, chemistry, geography and economics.

Confidentiality of information is an essential necessity in the information era, and cryptography is one of its protecting tools. Nowadays images are widely used in industrial process, and sometimes, these image data contain private or confidential information, therefore, it is important to protect them. Also this kind of data has some characteristic features such as huge amounts of data and the existence of patterns and backgrounds [3]. Because of these features, the common cryptosystem have some problems like being time-consuming and vulnerability to attacks. Digital image scrambling is an effective and common tool for image encryption and data hiding, whose main goal is to reorder and change the position of image pixels and break the relationship between adjacent pixels [4].

There has been a lot of effort in designing an efficient image scrambling method based on CA. Xiang Desheng and Xiong Yueshan [5], proposes a scheme for image scrambling Josephus traversing. Guodong Ye et al [6], proposed a chaos mapping algorithm with Logistic mapping algorithm. Ruisong Ye and Huiliang Li [7], proposed a scheme for image scrambling using chaotic CA (CCA) with different rule numbers (224 and 816). Recently, Abdel Latief Abu Dalhoum et al [8], proposed a novel method for scrambling digital images based on Two Dimensional Cellular Automata (2D CA), where the complex behaviour characteristics of this cellular automaton are analysed based on Lambda parameter. Here, we use their method as reference, modify it and we get good results as shown in the experimentation part.

• II.    cellular automata

A cellular automaton is used in Computer Science as a discrete model for implementing algorithms. It consists of a regular grid of cells, each in one of a finite number of states. The grid can be in any finite number of dimensions. For each cell, a set of cells called its neighborhood (usually including the cell itself) is defined relative to the specified cell. For example, the neighborhood of a cell might be defined as the set of cells a distance of 3 or less from the cell. An initial state (time t =0) is selected by assigning a state for each cell. A new generation is created (advancing t by 1), according to some fixed rule (generally, a mathematical function) that determines the new state of each cell in terms of the current state of the cell and the states of the cells in its neighborhood. Typically, the rule for updating the state of cells is the same for each cell and does not change over time, and is applied to the whole grid simultaneously, though exceptions are known.

As the image is a two dimensional, here we use 2D CA model. In a 2D CA the cells are arranged in a two dimensional grid with connections among the neighboring cells, as shown in the Figure (1). The central box represents the current cell (that is, the cell being considered) and all other boxes represent the eight nearest neighbors of that cell.

In our experiment, a rectangular regular grid is used to represent a digital image and each cell represents one pixel of the image. So initial configuration at t=0, is the original image. Before designing image scrambling method based on CA, it is necessary to determine the structure of the neighbors firstly. The structure of the neighbors mainly includes Von Neumann neighborhood and Moore neighborhood, discussed below;

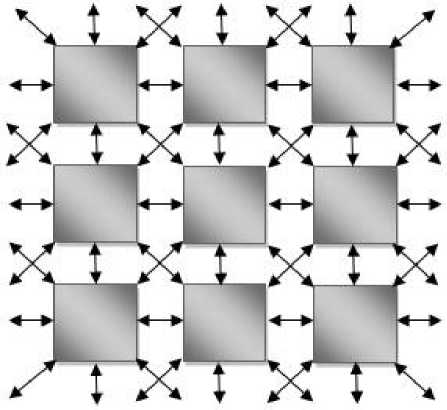
Figure 1: Network structure of 2D CA

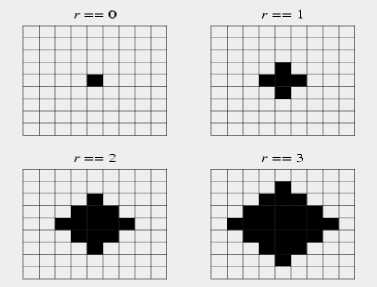
(a) Von Neumann neighborhood

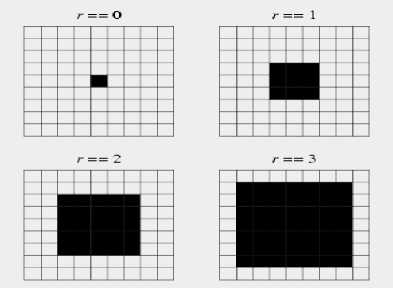
(b) Moore neighborhood

Figure 2: Structure of Neighborhoods

• •    Von Neumann Neighborhood

The Von Neumann neighborhood of a 2D CA is a diamond shaped neighborhood surrounding the cell (x 0 , y 0 ) and can be defined as follows [9]:

N(xo,y0) = {(x,y):| x - xо | + | y -yо < r}       (1)

By setting the radius to one, the neighborhood only consist of the cells in the immediate vicinity of the current cell, i.e. top, bottom, left and right. The neighborhood can be visually illustrated as seen in Figureure (2.1), for radii that vary from zero to three.

• •    Moore Neighborhood

The Moore neighborhood of a 2D CA is a square shaped neighborhood surrounding the cell (x0, y0) and can be defined as follows [10]:

Nm(xо,yо) = {(x, y):|x - xо l< r,1 y - yо l< r} (2)

The Moore neighborhood also defines a radius but differs from the Von Neumann neighborhood in that the Moore neighborhood includes neighbor cell on the diagonals, i.e. top-left, top-right, bottom-left and bottom-right. A visual illustration of the Moore neighborhood can be seen in Figure (2.2) for radii that vary from zero to three.

• III.    Game of life

John Horton Conway’s Game of Life (GoL) is a simple two-dimensional, two state CA, remarkable for its complex behaviour [11, 12, 13]. That behaviour is known to be very sensitive to a change in the CA rules. Previously, we have investigated CA GoL rules for noise filtering and edge detection and found beautiful results [14]. Here, we continue our investigations into its sensitivity to changes in the lattice, by the use of periodic boundary condition for digital image scrambling.

It consists of an [M × N] matrix of cells, where each cell may take only two states: alive (represented by one) or dead (represented by zero). Each cell has eight neighbors, according to the Moore neighborhood. At every time step, also called a generation, each cell computes its new state by determining the states of the cells in its neighborhood and applying the transition rules to compute its new state. Every cell uses the same update rule, and all the cells are updated simultaneously.

The next state of a cell is determined as follows:

• •    "Birth": A cell dead at time t becomes alive at time t+1 if exactly three of its neighbors are alive at time t.

• •    "Death by overcrowding": A cell alive at time t dies at time t+1 if four or more of its neighbors are alive at time t.

• •    "Death by exposure": A cell alive at time t dies at time t+1 if one or none of its neighbors are alive at time t.

• •    "Survival": A cell alive at time t will remain alive at time t+1 if two or three of its neighbors are alive at time t.

Mathematically, the overall evolutions rules of the GoL can be described as follows [18]:

^L 0, sum * 2,3

• ⁴         4), sum * 3

Note that the neighborhood defines a radius. This variable can be introduced to enlarge the neighborhood.

Where, S i,j (t) is cell state at time t=0, S i,j (t+1) is the cell state at time t+1 and sum is the number of “live” cells in the eight neighborhood cells.

• IV.    Digital image scrambling

Let P denote the original image, P ' denoted the output image and choose a random matrix A of same size as P with element 0 and 1, we then do the following steps.

• (1)    Apply the CA GoL rules to matrix A for k times, each time we obtain matrix sequences {A 1 , A 2 ,…, A k }.

• (2)    Get the gray value of pixel P(i, j) with A 1 (i, j) =1 successively and put it in matrix P ' by order.

• (3)    Take the gray value of remaining pixels of P(i,j) with A 1 (i,j)=0 successively and put it in matrix P ' by order. And finally we get the scrambled image P '.

In order to perform the scrambling with other sequences {A 2 ,…, A k }, repeat the steps (2) & (3). Further, to recover the original image the inverse of the scrambling algorithm must be executed. The keys in the proposed method are the matrix A and the number of generations [8].

Scrambling degree can us used to evaluate the advantage and disadvantage of scrambling schemes [7]. Assume that the size of digital image P is M × N. We first compute the gray difference between the pixel ( i , j ) and its four neighboring pixels as follows:

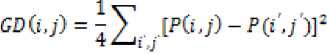
Calculate all GD ( i , j ) for the whole image except those pixels at four sides and take the mean

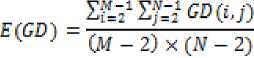
Let E ( GD ), E '( GD ) be the mean gray differences of the original image and the scrambled image respectively. The scrambling degree is defined as follows.

EXCO) - E(GD) E^ = EXGD) *GD(i,n

The value of GDD lies in [-1, 1]. We note that if GDD is more near 1, the better scrambling effect is obtained.

The experimental image is selected as the classical Lena image, whose size is 256×256. In order to evaluate the performance of CA based methods for digital image scrambling objectively, scrambled degree (GDD) between descrambled image and original image is used. Figure (3) shows the whole process of scrambled/descrambled process whereas Figure (3.1) is the original image, Figure (3.2) is the first generation produced by Standard CA GoL, Figure (3.3) is the scrambled image and Figure (3.4) is the descrambled image. Table (1) gives the GDD values for Lena image without boundary and with periodic boundary.

(a)

(b)

(c)

(d)

Figure 3 : Digital Image Scrambled/descrambled Process; (a) Input Image, (b) Matrix Sequence with k=8 (c) Scrambled Image and (d) descrambled Image

No. Of Generations	Lena
	GDD	GDD Von Neumann, Periodic Boundary	GDD Moore, Periodic Boundary
1	0.9284	0.9148	0.9141
2	0.9397	0.9280	0.9320
3	0.9321	0.9198	0.9181
4	0.9492	0.9397	0.9426
5	0.9323	0.9199	0.9188
6	0.9474	0.9374	0.9400
7	0.9454	0.9352	0.9346
8	0.9551	0.9465	0.9477
9	0.9366	0.9248	0.9247
10	0.9463	0.9363	0.9386
11	0.9440	0.9336	0.9340
12	0.9507	0.9414	0.9432
13	0.9444	0.9340	0.9344
14	0.9491	0.9393	0.9411
15	0.9488	0.9394	0.9387
16	0.9529	0.9440	0.9444
17	0.9427	0.9319	0.9320
18	0.9468	0.9365	0.9377
19	0.9451	0.9348	0.9350
20	0.9479	0.9381	0.9389

Table 1 : GDD results for Lena image with different generations and configurations

Image filtering can effectively reduce the noise and make the image smooth. The goal of impulse noise removal is to suppress the noise while preserving the integrity of edge and detail information, to reduce the degradation related to noise of any kind, a pre processing or filtering step could be applied [15]. We have already given many ways of image noise filtering based on cellular automata [16][17]. After applying any one of these methods, we get a noise reduced image as shown in Figure (5).

• V.   Conclusion