Digital image watermarking using DWT and FWHT

Published Online June 2018 in MECS DOI: 10.5815/ijigsp.2018.06.06

The process of embedding a message into an image is known as digital image watermarking. The development of the technologies with respect to the computer, network, and multimedia, the transmission of information in the form of images has become more and more convenient. The main applications of Digital Image Watermarking techniques are copyright protection, ownership, and authenticity. The problems occurring during transmission of information as an image have also placed a challenge to secure the intellectual properties of the images. To overcome these problems researchers invented a technique to embed some kind of information into the images for the sake of identification of the ownership. This process is termed as digital image watermarking. There are mainly two modules associated with the watermarking system, first is the watermark embedding module and the other is the watermark detection and extraction module. A number of algorithms are developed to insert a watermark and to extract a watermark from a given cover image. There exists different forms of watermarks according to human perception and are (1) Visible, (2) Invisible-robust, (3) Invisible-fragile, (4) Dual. A watermark that is perceptible is referred as the visible watermark and a watermark that is imperceptible is referred as the invisible watermark. A fragile watermark is a mark that is readily altered or destroyed when the cover image is modified through linear or nonlinear transformation and the combination of both visible and non-visible watermarks is referred as dual watermarks where, in this case, an invisible watermark is used as a backup for the visible watermark. The process of image watermarking is depicted in Fig.1.

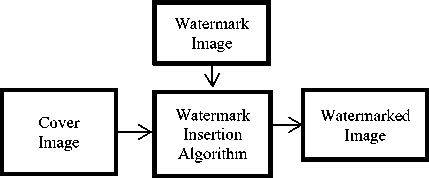
Fig.1. Generic Image watermarking process

An effective invisible digital watermarking technique should comprise of the following characteristic features and are; it should be highly imperceptible and it should be robust for the operations that are carried out on the images like cropping, rotation, scaling, filtering, collusion attacks etc. There are mainly two ways in which digital watermarking techniques are carried out, one in the spatial domain and the other in the frequency domain. The spatial domain watermarking techniques have less computational overhead than compared to the frequency domain watermarking techniques. Further, it is proved that the frequency domain digital watermarking techniques are more effective as compared to those of spatial domain watermarking techniques due to its imperceptibility and robustness characteristic features. In case of the spatial domain, the watermarks are embedded within the least significant bits of the cover image. A number of transformations are commonly used in the frequency domain; they include Fourier Transform (FFT, DFT, and WFT), Discrete Cosine Transform (DCT), Walsh-Hadamard Transform (WHT), Wavelet Transform (CWT, DWT, and FWT). The improvement in the performance of digital watermarking algorithms can be achieved with the usage of the number of transformations into the algorithms. This signifies that the usage of the combined transformations into the algorithms compensate the drawbacks of each other resulting in the development of the effective algorithms. In this paper, an attempt is made to combine the DWT and FWHT transformations to embed a watermark into the cover image and to extract the same watermark image from the same cover image. The Embedding of the watermark image is carried within the different sub-bands (LL, LH, HL, and HH) of the DWT transformation and the corresponding correlation values and the PSNR values are notified. The technique of hiding the images in all of the sub-bands concludes the selection of suitable sub-band of the DWT transformation for embedding the watermark image. The watermarked image is further subjected to different forms of attacks using different forms of noise and the corresponding PSNR and correlation values are calculated. The proposed watermarking technique using transformations is said to be robust when the watermark image is extracted easily from the cover image even if any of the attempts are made to change the contents of the data thereby degrading the cover image.

The paper proceeds with the following sections. In section II the related work concerned with the various approach of Digital Watermarking techniques are analyzed. Section III and IV describes the complete details concerned to the proposed methodology using DWT and FWHT transformations along with the proposed scheme. Section V describes the results of the algorithm in all of the sub-bands (LL, LH, HL, HH) of the DWT transformation with the inclusion of various noises and a comparison test is carried with the different watermarking techniques. Finally, section VI concludes the paper.

• II.    Related Work

Several different watermarking methodologies and techniques are designed and opted for various applications since many years.

(Dayanand G. Savakar and Anand Ghuli. 2017) have proposed digital watermarking scheme. The proposed scheme of Digital Watermarking comprises of both blind and non-blind Digital watermarking techniques within the process, this combined approach of digital watermarking can also be known as serial watermarking. The presented scheme is composed of mainly two stages, where the first stage involves the blind watermarking technique resulting to the embedding of a secret binary image into the first cover image and the output of the process is the first watermarked image, the second stage involves again embedding of the first watermarked image into the second cover image with the usage of non-blind approach. The stage-1 process of the blind watermarking process uses DWT (Haar) to extract the HL bands. Further stage-2 involves non-blind watermarking technique. In this case, the outcome of the stage-1 is fed as the input to the stage-2 and involves non-blind watermarking technique. This process involves the application of single-level DWT (Haar) on to the second cover image to establish lower frequency sub-band LL. Then the LL sub-band image is divided into red (R), green (G) and blue (B) components and SVD are applied to this each of these components to get computationally components as u, s and v matrices of the transformed image. This process is applied to the second cover image. Finally, the S components of the DWT applied over LL sub-bands of the second cover image and the first watermarked image are added with each of the R, G and B channel components and multiplied with a gain factor. Further, the same components are multiplied by the other U and V values of R, G, and B and concatenate them to retain the embedded watermarked image. Finally, the serial watermarked image is retrieved by the application of inverse DWT [1].

(Sandeep Kaur and Himanshu Jindal. 2017) have proposed a watermarking technique. The paper focuses mainly on watermarking techniques. The images are embedded as sample images into the cover image considering it as hidden information. The image when extracted is subjected to the image interpolation method this is to retain the quality of the image. The combination of the wavelets and interpolations provides a good quality enhanced and zoomed watermarked images during the time of encoding and decoding process. The main purpose of the interpolation technique is to get the hidden and improved information stored in the image. The methodology described concludes that the combination of the discrete wavelet transformation and interpolation in case of watermarking provides the PSNR value within the range 75.8826-80.9368 dB which implies that the 52% of better results are obtained when compared to the existing techniques [2].

(Anuja Dixit and Rahul Dixit. 2017) have given a review on a number of digital Image watermarking techniques. Further this paper describes and categorizes different watermarking techniques on the basis of their operating principles. Several watermarking techniques are discussed both in case of spatial domain and frequency domain. The popular method of watermarking technique in case of spatial domain is the LSB technique and the watermarking techniques discussed in case of frequency domain are the Discrete Cosine Transform, Discrete Fourier Transform, Discrete Wavelet Transform and further it is concluded that the frequency domain watermarking techniques are more robust than the watermarking techniques in case of spatial domain. And also different kind of attacks, requirements and their applications are also discussed. Some of the requirements of the digital watermarking which completely depend on the algorithm used for the watermarking are imperceptibility, robustness, security, complexity, and capacity are also discussed [3].

(Tamirat Tagesse Takore, et.al. 2017) have presented a scheme on robust image watermarking, that comprises of population-based stochastic optimization technique. The technique described as robust digital image watermarking is mainly based on edge detection and singular value decomposition. Further block based SVD process is carried out on the sub-images to embed a binary watermark with the modification within the singular value. A stochastic optimization technique that is based upon population is adopted to enhance performance while searching the embedding parameters that can maintain a better trade-off between robustness and imperceptibility. The experimental results conclude that the proposed method attains improved robustness against various image processing and geometric attacks and the comparison of the proposed scheme with the other schemes is carried out and the significant changes are observed. The quality metric of the watermarked images is shown by calculating the PSNR values which further concludes the proposed watermarking can achieve higher imperceptibility [4].

(Subin Bhajracharya and Roshan Koju. 2017) have proposed a method of robust digital image watermarking based on improved DWT-SVD. The watermarking technique is mainly concerned to color images. The method describes invisible robust digital watermarking based on Discrete Wavelet Transformations and Singular Value Decomposition in case of YCbCr color space. The comparison process is carried between the proposed scheme and some of the similar previous works based on which the performance of the proposed algorithm is identified. The performance is evaluated based on the PSNR and cross-correlation. By varying the values of scaling factor k and q two major tests imperceptibility and robustness are carried out along with the comparison test with another existing watermark algorithm. The paper concludes the proposed methodology is a non-blind digital watermarking which implies that there is a need for the cover image for the watermark extraction. The proposed scheme provides with the good value of PSNR signifying the rate of imperceptibility and with a high value of NCC that defines the robustness [5].

(Gökçen Çetinel and LLukman Çerkezi. 2016) have proposed a robust digital image watermarking methodology composed of RDWT and SVD. The proposed algorithm is based on mainly chaos-based digital image watermarking using redundant discrete wavelet transform(DWT) and singular value decomposition(SVD). Further the improvement with respect to the robustness and invisibility of the proposed methodology is established using the logistic mapping function to generate a chaotic image matrix that is serving as the watermark which is used further to modify the singular values of the low-frequency sub-band of the cover image that is obtained by the application of the RDWT. The method developed is shown to be robust against both the geometrical attacks and to the image processing attacks, and it also provides accurate watermark concealment via computer simulations. With the addition of chaotic signal as the watermark, the proposed scheme meets the security requirements. The analysis process shows that the RDWT is a shift-invariant that improves the robustness of the additive noises due to its redundancy. Three experiments where carried out to notify the effectiveness of the proposed scheme, in the first experiment the contribution of the SVD was demonstrated which showed that the SVD improved the imperceptibility of the scheme, then the second experiment was conducted to notify the advantage of exploiting chaos, the third experiment was conducted to compare a number of schemes with the proposed scheme and the conclusion is derived to be as the proposed method was shown to meet the characteristic features imperceptibility, robustness and security requirements [6].

(Dayanand G. Savakar and Anand Ghuli. 2015) have proposed a methodology of digital image watermarking using the discrete wavelet transformation, Fast Fourier transformation and Fast Walsh-Hadamard transformation. The methodology is mainly developed to study the sensitivity between robustness and fidelity. The proposed watermark embedding and extraction process using DWT, FFT,  and FWHT accustomed to digital image watermarking to study the sensitivity between robustness and fidelity. DWT is mainly used for locating the areas within the cover image that are much suitable to embed the watermark and the Fast Fourier transformation is used to convert the given input signal from spatial domain representation to frequency domain representation while the Fast discrete Walsh-Hadamard transformation returns the coefficients of the input signal. Finally, the watermark is embedded depending upon the pseudo-random sequence which is multiplied further with a constant gain factor into the predefined mid-band components of the block of the cover image, by varying the gain factor sensitivity of the watermark is analyzed. The experimental results show that the greater fidelity can be achieved by lowering the gain factor and the greater robustness can be achieved by the higher gain factor [7].

(Dayanand G. Savakar and Anand Ghuli. 2014) have proposed a methodology for digital image watermarking with the combination of DWT, chirp-Z and Fast Walsh Hadamard transformations. This combined approach of DWT, chirp-Z and Fast Walsh-Hadamard transformations in case of digital image watermarking is mainly used to minimize the gap between robustness and fidelity with limited capacity. The evaluation of the performance and the results show that the imperceptibility by the presence of the watermark is measured as 35.2584dB. Different noises are added to the watermarked image like Gaussian noise, Poisson noise, Salt and Pepper noise to achieve better robustness and demonstrated with different mean values and variances. Different image processing attacks like jpeg compression give a PSNR of 33.61dB. It is observed that the behavior of the algorithm with respect to the Gaussian noise when mean and variances are increased the correlation gradually decreases which declares that the algorithm is best suitable for Gaussian noise with the value of the mean being 0.4 and it is also declared that the algorithm behavior is feasible with multiple noises, compression, and cropping. Further, the experimental results show that the combined approach gives the acceptable PSNR value and the correlation of the retrieved watermark with the original is being 1. In this paper, the DWT is used to locate appropriate areas in the cover image for watermark embedding. The chirp z-transform is the z-transform for the given input signal along a spiral contour that is defined by a scalar. Fast discrete Walsh-Hadamard transform receives the input from the chirp z-transform and returns the coefficients of the input image. Further watermark is embedded depending upon the pseudo-random sequence into the already defined mid-band components of the block of the given cover image [8].

(S.Manikanda Prabu and Dr.S.Ayyasamy. 2014) have proposed a digital image watermarking technique based upon DWT and two dimensional Fast Fourier transformation approach. The experimental results further calculate the Peak signal to noise ratio and normalized cross-correlation coefficients are also computed to measure image quality for each transform. Further experimental results demonstrate that the proposed scheme is highly imperceptible and has good robustness for some common image processing operations and for some of the attacks. Peak signal to noise ratio (PSNR) is used to measure the quality of the image whereas Normalized Cross-Coefficient (NCC) is used to measure the difference between the original and extracted watermarks under various attacks. To inspect the robustness of the proposed scheme the watermarked image was subjected to several types of attacks and are JPEG compression, salt and pepper noise, gaussian noise, speckle noise, rotation and resizing. Then the comparison process of watermarking methods using FFT and using combined DWT-FFT is carried both in the presence and absence of noise. Fast Fourier transformation is used to convert given cover image from its spatial domain representation to frequency domain representation. DWT is a mathematical tool to decompose an image into four sub-bands and is lower approximation image (LL), horizontal (HL), vertical (LH), and diagonal (HH). The experimental results show that the proposed methodology has strong capability of embedding image and anti-attack. Moreover, the proposed watermarking scheme is more robust since it has the capability to keep the image quality well and achieves optimal NC values against several common image processing operations [9].

(Apoorv Tiwari, et.al. 2014) have proposed a digital image watermarking methodology based upon Fractional Fourier Transform and two dimensional Fast Fourier Transform with a number of attacks. In this methodology of watermarking the cover image is embedded with a watermark image further the watermarked image obtained is robust for a certain distortions which are caused due to the standard image processing. The watermarked image is subjected to different forms of malicious attacks. Signal to noise ratio (SNR) is calculated to measure the image quality for each of the transformation. The FRFT is interpreted as the rotation of angle α in the time-frequency plane [10]

(Hongqin Shi, et,. al. 2014) have proposed a digital image watermarking technique which is based upon blind approach. The technique is mainly concerned to the new color watermark embedding with a circulation that is based upon non-overlapping singular-value decomposition for hiding secret information within the cover images. The proposed scheme improves the robustness and security of the current watermark schemes. Further, the Experimental results and attack analysis show that the watermark algorithm is transparent and robust against some of the image processing operations [11].

(Jian-Guo Sun, et.al.2014) have proposed a method of reversible digital image watermarking for vector maps. The methodology described for reversible digital image watermarking mainly uses the technique of converting the watermarks into binary bits and further the binary bits are manipulated as the coefficients of neural networks for the purpose of embedding watermarks invisibly and also the weights of the neurons can be adjusted to fit into the neural coefficients which pick about the information of the watermark. The paper concludes with the fact that the performance of the algorithm is efficient to resist for the purposed attacks or to the unpurposed attacks [12].

(K.Sridhar, et.al. 2014) have proposed a paper into which the comparison test is established. The paper includes mainly comparison various digital watermarking techniques with the other data hiding techniques. The important techniques of data hiding that are compared with digital watermarking are steganography, cryptography, fingerprinting and digital signatures. Further, the paper concludes that watermarking technique of hiding data is more efficient than the other compared techniques as listed, due to its high security [13].

(Myasar Mundher, et.al.2014) have proposed a method for digital image watermarking for the purpose of security using discrete slantlet transformation. The paper describes the digital watermarking technique for true authentication. The technique comprises of the application of 2-level discrete slantlet transform on the cover image which divides into red, green and blue channels. The results that are produced exhibit robustness and the technique effectively extract watermark in the absence of original images [14].

(H.B.Kekre,et.al. 2013) have proposed a methodology to compare the performance of DCT and Walsh transforms in case of digital image watermarking using DWT-SVD. The scheme describes the robustness by the application of DCT to specific wavelet sub-bands and the further process is carried by factorizing the each quadrant of frequency sub-band with the usage of singular value decomposition. The process of embedding is done with the modification of singular values within the cover image. The comparison of performance of this technique is achieved by replacing the DCT with the Walsh transformation. Watermark image is embedded mainly in the three frequency sub-bands (HL2, HH2, and HH1). The comparison process proves that the embedding watermark in case of HH1 frequency sub-band confirms to be more robust and imperceptible than using HL2 and HH2 sub-bands. By analyzing the technique it is declared that, with the increase in scaling factor the quality of the cover image is degraded for both of the DCT and FWHT transformations. The paper concludes with, the loss of perceptibility is less when a watermark image is embedded in case of high frequency components of a cover image. The combination of Walsh transform with the DWT-SVD resulted in computationally faster watermarking scheme. The comparison process declares the robustness and imperceptibility provided by the combination of WHT-DWT-SVD is acceptable than with the combination of DCT-DWT-SVD [15].

(Mr.D.V.N Koteswara Rao, et.al. 2012) have proposed a method of digital image watermarking which is robust enough both for the external and internal attacks. The algorithm is designed using joint DWT-DCT transformations. Further experimental results show that the algorithm provides higher imperceptibility as well as higher robustness against common signal processing attacks [16].

(Koushik Pal, et.al.2012) have proposed a methodology for digital image watermarking for the purpose of data security using bit replacement algorithm technique along with the majority algorithm technique. In this paper, LSB watermarking technique is described which is carried out in the spatial domain along with its limitations. Then a new watermarking scheme is developed that uses a number of bits of the cover image that starts from the lower order till the higher order to embed the message into it [17].

(Gou in-like and Lu ran-ni. 2011) have proposed a method for digital image watermarking. The method mainly comprises discrete wavelet transformation. Discrete Wavelet multi-resolution decomposition algorithm is used to study watermarking algorithm using digital watermarking technology. Images are divided into three serial sub-graphs by the application of three-level wavelet decomposition. The serial graphs are divided into the high-frequency band and one sub-graph with the low-frequency sub-band. The experimental results show the algorithm is robust and the visual effect is quite satisfactory [18].

(Ali Al-Haj. 2007) proposed a methodology for digital image watermarking which is composed of the combination of discrete wavelet transformation and discrete cosine transformation. The proposed algorithm watermarks a given digital image using the combination of DWT and the DCT. The results of the performance evaluation showed that the combination of the two transforms improved the performance of the watermarking algorithms that are based solely on the

DWT transform. Performance evaluation metric involved is mainly robustness and imperceptibility based on which watermarking algorithms are evaluated. The paper concludes with, in case of DWT-based digital image watermarking approach, the combination of appropriate transforms with the DWT may lead to the positive impact on the performance of the watermarking system [19].

• III.    Methodology For Watermark Embedding

This paper describes an algorithm concerned with digital image watermarking which is developed by the combination of the two transformations: DWT and FWHT. In this section, a brief introduction to DWT and FWHT transformations is given.

The Discrete Wavelet Transform: The wavelet is defined as a small wave; hence wavelet analysis can be defined as, the analysis of a signal or an image with short duration finite energy functions. Wavelets are used in most of the applications especially in image processing and in compression techniques due to its low computational complexity of separable transforms. Wavelets are referred as the special functions which, in a form similar to sines and cosines in case of Fourier analysis and are used as basal functions. In case of 2-D images, applying DWT signifies processing the image by 2-D filters in each of the dimension. The input image is divided into four non-overlapping multiresolution subbands LL1, LH1, HL1, and HH1 where the sub-bands LL1 represents the coarse-scale DWT coefficients while the sub-bands LH1, HL1, and HH1 represents the fine-scale of DWT coefficients. To obtain the next fine-scale of wavelet coefficients, the sub-band HL1 is further processed until some fine-scale N is reached. Wavelets transform the image which is under investigation into another form which is more meaningful than before. This transformation process using wavelet is called as wavelet transformation. Choice of a particular wavelet depends mainly on the type of the application that is developed. Wavelet transform provides both temporal as well as frequency information, further, it exhibits multiresolution characteristic features, and wavelet transformation is mainly used in case of transients. Wavelets are mathematical functions that define certain criteria as a zero mean and are used for analyzing and representing images or other functions. DWT exhibits an outstanding property of spatio-frequency localization which signifies the DWT is appropriate to identify the areas within the cover image where a watermark can be embedded effectively. Hence the exploitation of the masking effect of the human visual system refers to if a DWT coefficient gets modified, only the region concerning to that coefficient gets modified. It is termed to be in general most of the image energy lies at the lower frequency subbands LLx where x=1,2,3,… thus embedding a watermark in these sub-bands leads to the degradation of the image significantly. The HHx sub-bands are referred to be as the high-frequency sub-bands which include edges and textures of the image which in turn any changes carried out to this sub-band will not be much sensitive to the human eye. Based upon this declaration thus the conclusion derived by many DWT-based watermarking algorithms is to embed the watermark within the middle frequency sub-bands LHx and HLx which corresponds to acceptable performance with imperceptibility and robustness. Fig.2 show’s all of the sub-bands concerned to the wavelet transform.

LL	LL1	HL2
	LH2	HH2
LH	HH

LL	HL
LH	LL1	HL1
	LH1	HH1

Matrix            Row

Н

1	1	1	1	1	1	1	1	0
1	-1	1	-1	1	-1	1	-1	1
1	1	-1	-1	1	1	-1	-1	2
1	-1	-1	1	1	-1	-1	1	3
1	1	1	1	-1	-1	-1	-1	4
1	-1	1	-1	-1	1	-1	1	5
1	1	-1	-1	-1	-1	1	1	6
L1	-1	-1	1	-1	1	1	-1	7

Fig.2. Multi-resolution DWT Sub-bands of the original image.

Walsh Hadamard Transform: Walsh Hadamard transform is referred as a non-sinusoidal orthogonal transform technique that is capable to decompose a signal/image into a set of its basic functions. The basis for Walsh Hadamard transform is the system of Walsh functions. These Walsh functions are orthogonal and have the values mainly +1 and -1. The general form of Walsh transform can be generated by the Hadamard matrix shown as:

From the above natural ordered Hadamard matrix sequency matrix can be constructed by changing the row ordering of the above matrix, based on the number of sign changes in each of the rows. The steps involved in the process of conversion of natural order matrix to sequency order are as follows, finding the grey code of the binary index code and then reversing it. An example of such transformation is given below. Which shows in the first step the conversion of binary code to the grey code and then the grey code bits gets reversed thus the value of k is obtained based upon which 8×8 sequency ordered matrix is obtained.

Н2к =

I Н₂ к-1 \.Н₂ к-1

Н 2 к-1

^-Н 2 ^к-1

S	0	1	2	3	4	5	6	7
Binary	000	001	010	011	100	101	110	111
Gray Code	000	001	011	010	110	111	101	100
Bit-reverse	000	100	110	010	011	111	101	001
K	0	4	6	2	3	7	5	1

Fig.3. Sample example to convert natural order matrix to sequency order

for к = 1,2,3,...... Н 1 =1 for k=0

Further for k =1 the Hadamard matrix Н ₂ for 2x2 can be defined as:

^Н =   -M             ⁽²⁾

For k=2 the Hadamard matrix Н ₄ the 4x4 can be defined as:

Thus an 8×8 sequency order Hadamard matrix can be given as:

Matrix           row sign changes

i 111 Н4 = [Н2 Н2 11 -Н2]   1 -1  1  -1 1  -1  -1 (3) 1 -1 -1  1 The output array of the WHT coefficients contains only the integer values, as a result of this, the Hadamard transform is referred as the very fast transform and thus

	1	1	1	1	1	1	1	1	0	0
	1	1	1	1	- 1	- 1	- 1	- 1	4	1
	1	1	- 1	- 1	- 1	- 1	1	1	6	2
Н5 8 =	1	1	- 1	- 1	1	1	- 1	- 1	2	3	(5)
	1	- 1	- 1	1	1	- 1	- 1	1	3	4
	1	- 1	- 1	1	- 1	1	1	- 1	7	5
	1	- 1	1	- 1	- 1	1	- 1	1	5	6
	. 1	- 1	1	- 1	1	- 1	1	- 1 .	1	7

can be implemented in O(N log ₂ N ) additions and subtractions. Further, it is proved in this paper, that Walsh Hadamard transform can be effectively used in the watermarking technique.

Natural and Sequence ordered WHT: By the application of the above definition repeatedly we can construct an 8×8 natural ordered matrix as shown in (4).

The sequency ordered Hadamard matrix organizes the transformed data in the increasing order of frequency which makes the process of feature selection systematic and fast. The main application of Walsh Hadamard transform is in speech processing, filtering, and power spectrum analysis. Walsh Hadamard transform has a fast

version, Further it is declared from the methodology that, in all of the cases 2-level DWT transformation is used both in case of watermark Embedding and in watermark extraction process to extract the all four sub-bands mainly LL, LH, HL and HH subbands since HL and LH bands are referred for their very clear horizontal edges and also they are useful in locating the suitable areas for embedding the secret watermark image. FWHT block is used to process all the four sub-bands of DWT using the block-wise technique. Then the random numbers that are uniformly distributed are generated with the help of a given key image which is of size 1x35. With these, separate sequences of pseudo-random numbers are stated for 0’s and 1’s respectively and are known as pn_sequence_0 and pn_sequence_1. The block structure is framed as shown in the Fig.3.

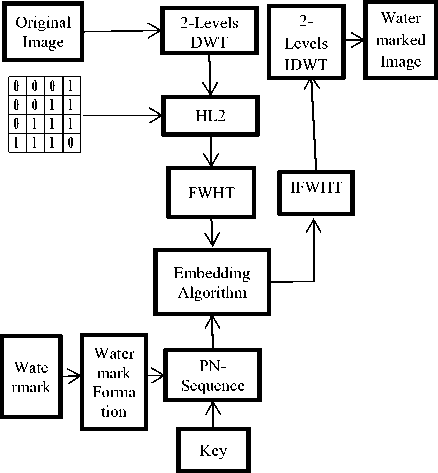
Fig.4. Combined DWT-FWHT Watermark embedding procedure

0	0	0	1
0	0	1	1
0	1	1	1
1	1	1	0

Fig.5. Sample of 4×4 Binary Sequence block used (For watermark Embedding and extraction)

The procedure of watermark Embedding and the extraction process is depicted in Fig.4 and Fig.6 and the steps that are carried-out are mentioned in the algorithm1 and algorithm2.

Algorithm1: Watermark Embedding

Start

Step1:  Read cover image

Step2:  Read Watermark image

Step3:  Resize cover image

Step4:  Apply DWT Transform to decompose the cover image into four non-overlapping multiresolution sub-bands like LL, HL, LH, and HH.

Step5:  Select HL subband and apply DWT again to get further sub-bands LL1, HL1, LH1, and HH1.

Step6:  Reformulate the binary image into a vector of

Zeroes and ones. Generate two uncorrelated pseudorandom sequences where one sequence is used to embed the watermark bit ‘0’ while the other sequence is used to embed the watermark bit’1’. A further number of elements in each of the two pseudorandom sequences must be equal to the number of mid-band elements of the FWHT-transformed DWT sub-bands.

Step7:  Scan HL1 image from left to right with a 4x4

mask of 0 and 1 and during the process of scanning apply FWHT on each block.

Step8:  Embed the generated two pseudo-random

Sequences i.e PN_0 and PN_1 applying a gain factor α within the FWHT transformed 4x4 blocks of the selected DWT sub-bands of the cover image. Embedding process is applied only to the mid-band FWHT coefficients. If the matrix of the mid-band coefficients of the FWHT transformed block is referred as X then: If the watermark bit is 0 then

X’=X+α×PN_0 else

If the watermark bit is 1 then X’=X+α×PN_1

Step9:  Apply inverse FWHT to each of the blocks after its mid-band coefficients have been modified to embed the watermark bits as described in the above step.

Step10: Apply inverse DWT on the DWT transformed image including the modified sub-band, to produce the watermarked cover image.

Step11: Add different noise and test the fragility

Step12: Repeat steps from step5-to-step11 by electing HH, HL, and LL sub-bands

Stop

• IV.    Methodology For Watermark Extraction

The steps involved in extracting a watermark from a given watermarked image are mentioned in the below algorithm2. The extraction procedure involves reading of an image into which another data is embedded using some kind of procedure. The watermarked image that is under consideration is subjected to Discrete Wavelet transformation and decomposed it into LL, LH, HH and HL sub-bands. The transformations are mainly used to convert the data into another format which is more suitable to carry out further processing. By the application of the Discrete Wavelet transformation to the HL, HH, LH and LL sub-bands of the decomposed image, another set of four sub-bands namely LL1, LH1, HH1, and HL1 are obtained. Further, the procedure involves selection of the sub-band one after the other namely HL1, HH1, LH1 and LL1. These sub-bands HL1, HH1, LH1 and LL1 is subjected to division process where the result is out as a 4×4 blocks. The extraction process involves another transformation known as Fast Walsh Hadamard transformation that is applied to each block of the subband that is under consideration and the corresponding mid-band coefficients of each FWHT transformed block is extracted. The generation of the two pseudorandom sequences using the procedure is carried out during embedding process and the procedure is repeated. Further, the individual blocks within the sub-band HL1, HH1, LH1 and LL1 corresponding correlation between the midband coefficients and the two generated pseudorandom sequences are calculated. The correlation having PN_0 is higher than the correlation with PN_1 then the watermark extracted is considered to be ‘0’ else watermark extracted is considered to be 1. Finally, the watermark image is reconstructed using the bits of the watermark those are extracted and calculate the difference between the original watermark and extracted watermark. The procedure is repeated in all the cases of sub-bands LL, LH, and LL sub-bands.

Algorithm2: Watermark Extraction

Start

Step 1: Read watermarked image

Step 2: Decompose the Watermarked image into four non-overlapping sub-bands LL, LH, HH, HL using DWT.

Step 3: Apply DWT to HL sub-band of the image to get four smaller sub-bands LL1, LH1, HH1 and HL1 choose the sub-band HL1.

Step 4: Divide the sub-band HL1 into 4×4 blocks

Step 5: Apply FWHT to each block within the chosen sub-band and extract the mid-band coefficients of each FWHT transformed block.

Step 6: Regenerate the two pseudorandom sequences using the same procedure used in watermark embedding

Step 7: For each block in the sub-band HL1 calculate the correlation between the mid-band coefficients and the two generated pseudorandom sequences. If the correlation with the PN_0 was higher than the correlation with PN_1 then the extracted watermark is considered to be 0, otherwise, the extracted watermark is considered 1.

Step 8: Reconstruct the watermark image using the Watermark bits those are extracted and estimate the similarity between the original and extracted watermark.

Step 9: Repeat the steps from step 3 to step 8 by choosing the LL, LH, and HH sub-bands

Stop

The extraction process involves the comparision of the extracted watermark image with the original watermark image using the statistical measure correlation. The degradition obtained within the extracted watermark image is notified with the addition of number of noises. The values of the correlation obtained nearer to 1 are referred to be the acceptable values and the values obtained qual to 1 are referred to be the accurate values. The procedure is repeated by selecting the sub-bands of the DWT transformation one after the other and respective PSNR values and the correlation value is notified. The values are notified in both the cases either of using the noise for watermark images or without using the noise. The extracted watrmark image in case of the LL sub-band of the DWT transformation is much different as compared to the extracted watermark images obtained by selecting the other sub-bands. Similarly the values of PSNR and correlation establish a large difference in values when compared LL sub-band with the other sub-bands.

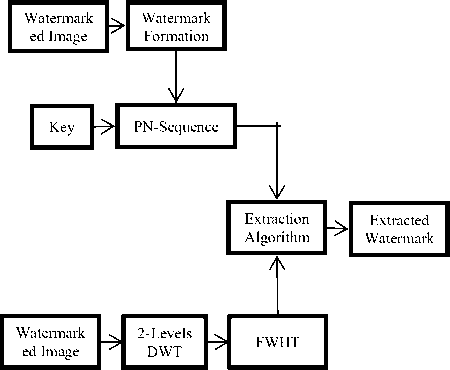
Fig.6. Combined DWT-FWHT Watermark Extraction Procedure

• V.    Results And Discussion

Quality of an image is a major characteristic feature of an image that measures the perceived image degradation. There exist several kinds of techniques and metrics that are capable enough to measure objectively and automatically that are evaluvated by a computer program. Different forms of quality metrics are explained.

MSE : In case of statistics MSE is termed as a mean squared error of a procedure that is responsible for estimating an unobserved quantity, measures the average of the squares of the deviations i.e calculates the difference between the procedure value and what is estimated. The MSE value is always non-negative and the values nearer to zero are better. MSE is one of the earlier methods of testing the similarity between the two images. A function can be established from (6).

m.s.e = 1Z?=i№-;o2 (6)

In case of watermark extraction process, the same key is utilized to extract the watermark from the cover image; the sample procedure can be depicted in the Fig.8.

Fig.8. Watermark Extraction Process

PSNR : The term peak signal-to-noise ratio(PSNR) can be defined as an expression describing the ratio between the power of the maximum possible value of a signal and the power of distorting noise that affects the quality of its representation. The units for PSNR is expressed in terms of the logarithmic decibel scale. The (7) represents PSNR.

Experiment utilizes a set of bitmap cover images that are shown in the below Table.1. The set of cover images is of eight in number.

Table 1. Cover Images Used in the Experiments

____ _    ___ 25 —1

20ps\H 2O,og...;

Cover Image 5

Cover Image 2

Cover Image 6

Cover Image 3

Cover Image 7

Cover Image 4

Cover Image 8

Where the mean square error (MSE) can be stated as the squared norm of the difference between the data x and the approximation x’ being the input data divided by the number of elements.

Correlation : It is a technique to perform the comparison process on an image before it is processed and after processing, where the image under consideration is referred as the reference image and the same image after processing is referred as the test image. The formula for the correlation process can be stated as from (8).

_     2i (X i -X m )(y i -y m )

72 i(X i -X m ) ² V2 i(y i -y m ) ²

Where X / and у / from the above-given (8) are referred as the intensity values of the i ^th pixel of the original watermark image and the processed watermark image and also x _m and y _m are referred as the mean intensity values of the original watermark image and the retrieved watermark image in case of digital watermarking.

Based on the above qualitative metrics, digital image watermarking algorithm and watermark extraction algorithm that is proposed in this paper shows the acceptable range of values for a given set of *.bmp images. The cover image of a given size that has to be watermarked is reduced to a fixed sized 512×512 image. Key is generated to insert the watermark into the cover image and the same key is utilized for the watermark extraction. Fig.7 shows a sample diagram representing the main blocks of the scheme in case of watermark embedding

Fig.7. Watermark Embedding Process

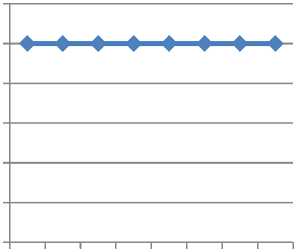
According to the Table.2, it can be explained that for a given set of images the correlation between the original watermark image and the extracted watermark image is equal to 1 which is acceptable, and the size being constant of both cover image and watermark image and also the PSNR values for the chosen set of images are also within the acceptable range, maximum value being 35.3950dB and the minimum value is 35.0699dB in case of HL sub-band. Further to test the fidelity and the robustness of the given watermark image a process is carried out that adds different forms of noises for the watermarked image like Gaussian, Poisson, Salt and Pepper and Speckle noises. After the Embedding of noise into the watermarked image still, the PSNR values for the same set of images are within the acceptable range along with the correlation values for HL sub-band. This can be seen by referring to the table 2, 3, 4 and 5, where the Table. 3 shows the acceptable correlation values for the same set of images with the addition of Gaussian noise to the watermarked image with the extracted watermark images and Table.4 shows the acceptable correlation values for the same set of images with the addition of Poisson noise to the watermarked image and Table.5 shows the acceptable correlation values for the same set of images with the addition of salt and pepper noise to the watermarked image and Table.6 shows the acceptable correlation values for the same set of images with the addition of speckle noise to the watermarked image. The procedure is repeated and the corresponding PSNR and correlation values are notified in case of LL, LH, and HH sub-bands of the DWT transformation. In case of all the sub-bands 2-level DWT is applied. Table.7 shows the watermarked images with the correlation and PSNR values for the same set of images in case of HH sub-band of DWT transformation. With the addition of various noises the correlation values are notified in Table. 8, 9, 10, and 11 in case of HH sub-band. Table.12 shows the watermarked images along with the corresponding PSNR and correlation values within the LH sub-band of the DWT transformation. With the addition of different noises in LH sub-band the results of correlation are mentioned in the Table.13, 14, 15 and 16. Embedding of the watermark image is also performed in case of LL subband of the DWT transformation. Table.17 lists the values of the PSNR and correlation along with the extracted watermarked image. With the inclusion of noise for the same set of watermarked images the values of PSNR and correlation values along with the extracted watermark image is shown within the Table.18, 19, 20 and 21. The values obtained with the same process in all the sub-bands and by analyzing the extracted watermark image from the tables, signifies that the maximum energy of an image lies at the lower-frequency sub-bands i.e LLx this notifies the procedure of embedding watermark applied to this sub-band may degrade the quality of the image but might increase the robustness. The HHx subbands referred to the high-frequency sub-bands, embedding watermark in these sub-bands leads to the imperceptible watermark Embedding. Hence based on the above results it is concluded that the embedding the watermark in case of the middle frequency sub-bands LHx and HLx could achieve the acceptable performance of imperceptibility and robustness. The experiment carried-out shows most of the inputs and outputs that are identified and specifies the sub-bands that is most suitable to embed the watermark. The method is applied only to the bitmap images and can also be extended to various forms of images to analyze the robustness and imperceptibility of the images.

Table 2. Correlation and PSNR values for a set of watermarked images in case of HL sub-band without noise

Cover Image	Waterma rk Image	Water marked Image	Extracted Watermar k Image	PSNR (dB)	Corr elati on
	Copyright	Й!	Copyright	35.1279	1
1 -^^1	Copyright	BB1 _ЫН_	Copyright	35.3950	1
№	Copyright		Copyright	35.0699	1
	Copyright	Hi	Copyright	35.3052	1
|4	Copyright	В	Copyright	35.0935	1
^^^	Copyright	e	Copyright	35.2026	1
1 ■> 1 ^	Copyright	In i ,i	Copyright	35.1193	1
кд ^	Copyright	j^	Copyright	35.1293	1

Table 3. Correlation for different images with the addition of Gaussian noise in case of HL sub-band

Waterm arked Image	Waterma rk Image	Extracted Watermark Image	Correlation
6	Copyright	Copyright	0.9895
в	Copyright	Copyright	0.9589
s	Copyright	Copyright	1
	Copyright	Copyright.	0.9947
	Copyright	Copyright	1
	Copyright	Copyright	1
к	Copyright	Copyright	1
it	Copyright	Copyright	1

Table 4. Correlation for different cover images with the addition of Poisson noise in case of HL sub-band

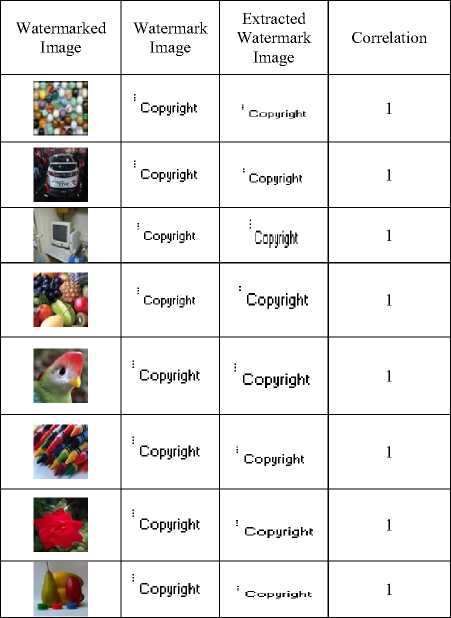
Table 5. Correlation for different cover images with the addition of Salt and Pepper noise in case of HL sub-band

Watermark ed Image	Watermar k Image	Extracted Watermark Image	Correlation
	Copyright	Copyright	1
|яЛ	Copyright	Copyright	1
	Copyright	Copyright	1
	Copyright	Copyright":	1
	Copyright	Copyright	1
^	Copyright	Copyright .	1
■	Copyright	Copyright	1
	Copyright	Copyright	1

Table 7. PSNR values and Correlation for a set of images in HH subband without noise

Cove r Imag e	Waterma rk Image	Water marke d Image	Extracted Watermark Image	PSNR	Correlat ion
^^i	Copyright		Copyright	35.1283	1
■M JBH	Copyright		Copyright	35.3961	1
15	Copyright		' Copyright	35.0731	1
я	Copyright	H	Copyright	35.3056	1
	Copyright	E	Copyright	35.0935	1
Ш	Copyright	Ж	Copyright	35.2033	1
■	Copyright		Copyright	35.1194	1
	Copyright	it	Copyright	35.1298	1

Table 6. Correlation for different cover images with the addition of Speckle noise in case of HL sub-band

Waterm arked Image			Waterma rk Image	Extracted Watermark Image	Correlation
			Copyright	"yCppyright	0.9118
EH			Copyright	Copyright	0.9844
	. r		Copyright	Copyright	0.9895
			Copyright	Copyright1:	0.857
			Copyright	'Copyright	0.9589
			Copyright	Copyright	0.9846
			Copyright	Copyright	0.9596
■ ■re			Copyright	'Copyright	0.9947

Table 8. Watermarked Images with the correlation values after the embedding of Gaussian noise in HH sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright	О о p у г i g h t	0.9947
EH	Copyright	Copyright	0.9841
15	Copyright	Copyright	1
	Copyright	Copyright	0.9844
	Copyright	C ■=■ p у г i g h t	1
	Copyright	Copyright	1
■	Copyright	Copyright	1
M	Copyright	Copyright	1

Table 10. Watermarked Images with the correlation values after the Embedding of Salt and Pepper noise in HH sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright	Copyright	0.9743
	Copyright	Copyright	0.9589
	Copyright	Copyright	0.9947
	Copyright	Copyright	0.9502
^	Copyright	Copyright	0.9895
	Copyright	Copyright	0.9645
н	Copyright	Copyright	0.9844
я	Copyright	Copyright	0.9693

Table 12. Embedding watermark in case of LH sub- band without the use of noise and calculation of PSNR and correlation

Cove r Imag e		Waterma rk Image	Water marke d Image	Extracted Watermark Image	PSNR	Correlat ion
и v i		Copyright		Copyright	35.1254	1
1 W		Copyright	■SI	Copyright	35.3932	1
		Copyright		Copyright	35.0685	1
я		Copyright	я	Copyright	35.3022	1
		Copyright	и	Copyright	35.0914	1
	ул	Copyright	^	Copyright	35.2001	1
E		Copyright	II	CoMiiaht	35.1189	1
M		Copyright	^j^	Copyright	35.1275	1

Table 13. Watermarked Images with the correlation values after the Embedding of Gaussian noise in LH sub-band

Watermarked Image			Watermark Image	Extracted Watermark Image	Correlation
	*7j vi		Copyright	Copyright	0.9947
	ы 7		Copyright	Copyright	0.9895
			Copyright	Copyright	0.9947
			Copyright	Copyright	0.9895
	р ।		Copyright	Copyright	0.9847
	^		Copyright	Copyright	0.9947
	■		Copyright	Copyright	0.9947
			Copyright	Copyright	0.9895

Table 15. Watermarked Images with the correlation values after the Embedding of Salt and Pepper noise in LH sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright	Copyright	0.9793
	Copyright	Copyright-	0.9502
	Copyright	Copyright	0.9793
	Copyright	Copyright	0.9693
я	Copyright	Copyright-	0.9743
^	Copyright	Copyright	0.9633
H	Copyright	Copyright-	0.9693
	Copyright	Copyright	0.9693

Table 9. Watermarked Images with the correlation values after the embedding of Poisson noise in HH sub-band

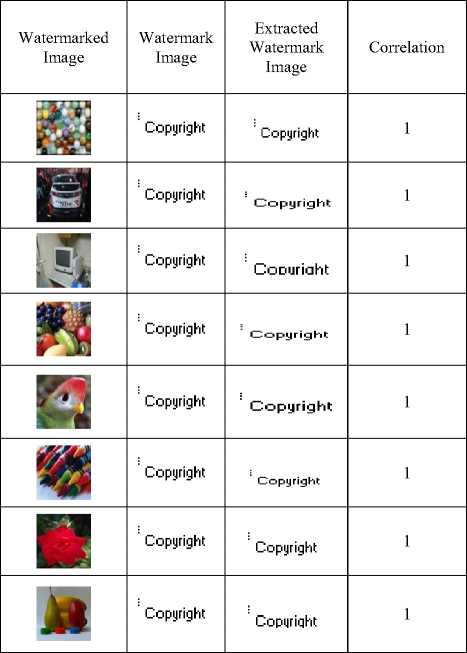
Table 11. Watermarked Images with the correlation values after the Embedding of Speckle noise in HH sub-band

Watermarked Image			Watermark Image	Extracted Watermark Image	Correlation
	1		Copyright	/Copyright .	0.9118
	7		Copyright	Copyright	0.9895
			Copyright	Copyright	0.9793
	Й		Copyright	Copyright.	0.9047
			Copyright	Copyright	0.9410
	8		Copyright	Copyright	0.9541
		г	Copyright	Copyright	0.9334
			Copyright	Copyright	0.9947

Table 14. Watermarked Images with the correlation values after the Embedding of Poisson noise in LH sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright	Copyright	1
	Copyright	Copyright	1
	Copyright	Copyright	1
	Copyright	Copyright	0.9947
ti	Copyright	Copyright	1
	Copyright	Copyright	1
■	Copyright	Copyright	1
	Copyright	Copyright	1

Table 16. Watermarked Images with the correlation values after the Embedding of Speckle noise in LH sub-band

Watermarked Image			Watermark Image	Extracted Watermark Image	Correlation
			Copyright	'Copyright	0.9364
			Copyright	Coouriaht	1
	JS		Copyright	■Copyright	0.9793
			Copyright	Copyright-,-	0.8532
в			Copyright	Copyright ■	0.9455
			Copyright	'■Copyright	0.9466
	и		Copyright	Copyright	0.9840
	j»		Copyright	■Copyright-	0.9793

Table 17. Embedding watermark in case of LL sub-band without the use of noise and calculation of PSNR and correlation

Cover Image	Waterma rk Image	Waterma rked Image	Extracted Waterma rk Image	PSNR	Correlati on
a	Copyright		К ИНИ	35.1199	0.0911
в	Copyright		в	35.3522	0.3278
15	Copyright	IS		35.0572	0.0581
Гд^<1 lz 1	Copyright		5ВЙЯ8	35.3012	0.1353
11	Copyright	^j		35.0824	0.0344
□	Copyright	^^^^	^v^^Si	35.1712	0.1664
п	Copyright	1	■	35.1100	0.2173
	Copyright	^1^		35.1127	0.0662

Table 19. Watermarked Images with the correlation values after the Embedding of Poisson noise in LL sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright		0.0911
Bi	Copyright		0.3278
	Copyright		0.0581
	Copyright		0.1365
	Copyright		0.0377
	Copyright	1MI	0.1659
	Copyright		0.2157
	Copyright		0.0662

Table 18. Watermarked Images with the correlation values after the Embedding of Gaussian noise in LL sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright	КЯ8К	0.0802
	Copyright	^№	0.2393
	Copyright		0.0377
	Copyright	УЦЩДН	0.1167
	Copyright		0.0361
	Copyright	KSM	0.1252
	Copyright	■	0.1680
	Copyright		0.0560

Table 20. Watermarked Images with the correlation values after the Embedding of Salt and Pepper noise in LL sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright		0.0810
	Copyright	!■	0.2722
	Copyright		0.0571
	Copyright		0.1216
	Copyright		0.0423
i	Copyright		0.1450
■	Copyright	^■E	0.1739
в	Copyright		0.0633

Table 21. Watermarked Images with the correlation values after the Embedding of Speckle noise in LL sub-band

Watermarked Image	Watermark Image	Extracted Watermark Image	Correlation
	Copyright	ИМИ	0.0918
	Copyright	в»	0.3304
iSe	Copyright		0.0592
	Copyright	шаив	0.1324
в	Copyright		0.0361
	Copyright	EM	0.1653
ы	Copyright	■	0.2162
■	Copyright		0.0662

The analysis process further includes a comparison test describing the comparisons carried on the perceptual characteristic features between the cover image and the watermarked image in the proposed scheme for HL subband of the DWT transformation with the perceptual characteristics features of the cover image and the watermarked image of other schemes. The perceptual characteristic feature between the cover image and the watermarked image in all the schemes that are described in the comparison process are measured using the qualitative metric PSNR and the unit is in dB. The comparison test described so far is depicted in the Table.22. The comparison process shows that the proposed scheme holds the values of PSNR that are necessary to be in the valid range as compared to the other schemes. Since each of the compared schemes consists of different transformations to insert watermark image and to retrieve the watermark image. Each of the noises added to the watermarked images is of minimum value based upon which the fidelity test is carried out. The main characteristic feature of the digital watermarking system is to secure the data; if it is termed to be an insecure system then the system is assumed to be invalid for practical applications. Thus the proposed scheme attains the necessary security parameter conclusively. The use of DWT transform is to apply a pair of low-pass and high-pass filters then the application of downsampling is carried out to these filtered coefficients. Further, the output of the low-pass filter contains the low-frequency components of the image after the process of downsampling which is an approximate part of the original image and the output of the high-pass filter contains high-frequency components that are termed as the details of the original image.

Table 22. Comparison of the Proposed Scheme with the other Schemes

Perceptual Similarity Between Cover Image and Watermarked Image (PSNR in dB) (Proposed Scheme)	Perceptual Similarity Between Cover Image and Watermarked Image (PSNR in dB) (Scheme of Reference) 1	Perceptual Similarity Between Cover Image and Watermarked Image (PSNR in dB) (Scheme of Reference) 4	Perceptual Similarity Between Cover Image and Watermarked Image (PSNR in dB) (Scheme of Reference) 10	Perceptual Similarity Between Cover Image and Watermarked Image (PSNR in dB) (Scheme of Reference) 12	Perceptual Similarity Between Cover Image and Watermarked Image (PSNR in dB) (Scheme of Reference) 13
35.0699	25.6160	42.2393(FFT)	45.32(red channel)	42.1347	97.072(HL2)
To	To	To	To	To	To
35.3950	75.2263	48.0339(DWT+FFT)	58.97(Blue Channel)	42.893	97.083(HH2)

Graphical representations of correlation and PSNR values for various cover images for a given specific sized watermarked image without the embedding of noise in case of HL sub-band of DWT transformation, the values can be depicted according to table.2 can be shown in Fig.9 and Fig.10. Similarly the values obtained in case of LL, LH and HH sub-bands can also be shown on graphs.

Graphical representation of correlation for various cover images and for a given specific sized watermark image with the embedding of gaussian noise into the watermarked image in case of HL sub-band can be shown in the Fig.11. Similarly, a graphical representation of correlation for various cover images and for a given fixed sized watermark image with the Embedding of poison noise into the watermarked image can be shown in the Fig.12. The case is repeated and few more graphical representations are shown in below Fig.13 and Fig.14 with the Embedding of salt and pepper noise and speckle noise into the watermarked image. The diagrams depict in all the cases that, the original watermark image and the watermark image that is retrieved from the cover image after processing is similar or almost similar.

я

1.2

0.8

0.6

0.4

0.2

Cover Images

1.2

а 0.8

0.6

5 0.4

0.2

Cover Images

Fig.12. Correlation for different forms of images using poisson noise from Table.4

Fig.9. Correlation between a set of Images without noise from Table.2

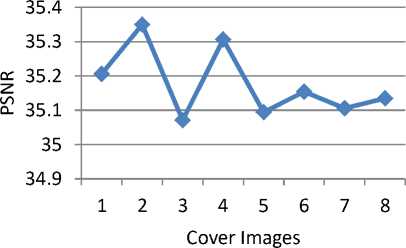
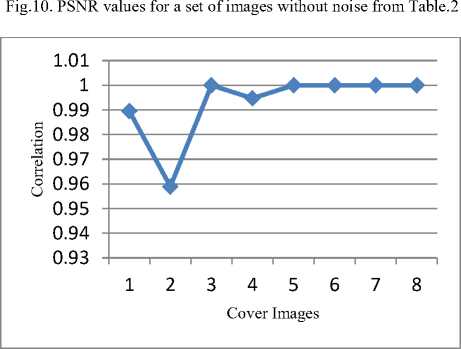
Fig.11. Correlation for different forms of images using gaussian noise from Table.3

0.98

0.96

0.94

0.92

0.9

0.88

0.86

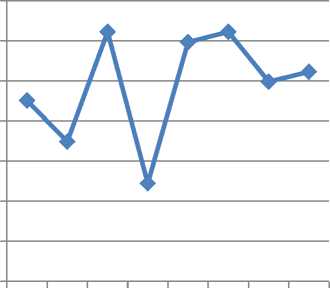
Cover Images

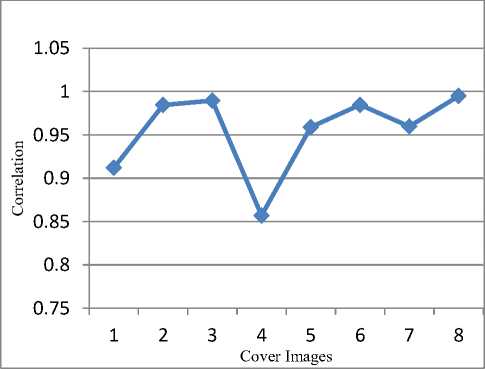
Fig.14. Correlation between different forms of images using speckle noise from Table.6

• VI.    Conclusion

Digital image watermark embedding and retrieval is proposed and tested successfully with DWT and FWHT transformation. It is found that the proposed method is robust against band attacks. For a given watermark of fixed size and for a given set of RGB cover images (*.bitmap), irrespective of the size of the cover images, the PSNR values for the watermarked images lies between 35db-40db and the correlation between the watermarked images before processing and after processing lies between 0.5-1.0 for the combination of DWT and FWHT transformation in case of HL sub-band of DWT transformation. Similarly after the inclusion of any of the noise (Gaussian, Salt, and Pepper, Poisson, Speckle) into the watermarked images for the combination of DWT and FWHT transformations still the PSNR values are valid within the range 35db-40db and the correlation between the watermarked image before processing and after processing lies between 0.5-1.0. The process is repeated with the combination of DWT and FWHT for embedding the watermark in all of the subbands (LL1, LH1, and HL1) of the DWT transformation and notifying the corresponding PSNR values and the correlation values.