Динамическая модель распространения волн от ударного импульса в составном стержне с учетом трения
Автор: Яновская Елена Александровна, Сосенушкин Евгений Николаевич, Иванова Оксана Константиновна
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 1-2 т.18, 2016 года.
Бесплатный доступ
В статье рассматривается динамический процесс мгновенного возбуждения стержней из композиционных материалов ударными импульсами ступенчатой формы. Два упругих стержня взаимодействуют между собой по закону сухого трения после приложения ударной нагрузки к более жесткому стержню. В результате определяются скорости взаимодействия и напряжения, возникающие в материале стержней.
Динамическая модель, сухое трение, упругий стержень, композиционный материал, волна, скорость, амплитуда, напряжение
Короткий адрес: https://sciup.org/148204394
IDR: 148204394 | УДК: 539.3
Текст научной статьи Динамическая модель распространения волн от ударного импульса в составном стержне с учетом трения
компактирования с наложением высоких давлений, а в некоторых случаях температур, и сложной технологии спекания [19]. В дисперсионных композиционных материалах основная нагрузка приходится на материал матрицы, а распределенные по объему дисперсные частицы упрочняют ее, препятствуя пластической деформации [20, 21] или разрушению [22, 23]. В волокнистых КМ основную нагрузку несут высокопрочные волокна, а матрица связывает волокна, защищает их от воздействия внешней среды и придает материалу нужные физико-механические характеристики (электро- и теплопроводность, коррозионную стойкость и др.).
КМ, в которых компоненты обычно расположены с определенной периодичностью, представляют интерес из-за их способности ослаблять ударные импульсы [10]. Чрезвычайная сложность взаимодействия волн при распространении ударного импульса в реальном КМ приводит к тому, что современные теоретические методы исследования этой проблемы ограничиваются сильно идеализированными моделями.
Ограничения модели. Предположим, что некоторые КМ можно заменить соответствующими моделями [7-10]. Рассмотрим динамические процессы в материалах, армированных волокнами, которые можно представить как составные стержни. При воздействии на подобные материалы динамическими нагрузками значительная часть энергии рассеивается за счет наличия сил трения между поверхностями контакта стержней. Рассмотрим полубесконечный составной стержень, состоящий из 2 слоёв. Каждый из слоёв будем считать упругим стержнем постоянного поперечного сечения S . Часть поверхностей этих стержней с периметрами нормальных сечений L взаимодействуют друг с другом по закону сухого трения Кулона [24]. В случае, когда имеет место проскальзывание между стержнями, касательные напряжения на боковой поверхности будут равны fN, где N боковое давление на стержне, а f - коэффициент трения между материалами стержней.
При наличии относительного движения между стержнями на их поверхностях будет действовать предельная сила трения, абсолютное значение которой, отнесенное к единице длины стержней для случая сухого трения равно Ff=fLN [24]. Эта сила всегда действует в направлении, противоположном вектору скорости относительного движения сечений. При отсутствии проскальзывания сила трения принимает некоторое значение, не превышающее по абсолютной величине предельное. Будем считать величину силы трения постоянной.
Характер взаимодействия. В данной работе рассматривается случай мгновенного возбуждения стержней импульсами ступенчатой формы. Удар производится по более жесткому стержню. Рассмотрим два упругих стержня, взаимодействующих между собой по закону сухого трения. Считаем, что для первого стержня модуль Юнга имеет значение E 1 и плотность ρ 1 , для второго – E 2 и ρ 2 Продольные упругие волны, которые распространяются в стержнях, имеют соответ-
E E 2
ственные скорости a1 = J и a 2 - J— ■ Будем считать, что a 2 > a 1 . Начало координат поместим на ударяемом конце второго стержня и направим оси х вдоль стержня (рис. 1).
„ - x qx
G 2 = "Г
— E 2 f ( a 2 t — x ) + E 2 ф ( a 2 t + x )
Постановка задачи и её решение графоаналитическим методом. Для ударяемого стержня σ 2 и υ 2 довлетворяют системе (2). В момент t=0 все сечения стержня, за исключением x =0, считаем неподвижными
и ненапряженными, т.е.
g = u = 0 при t = 0 и x > 0. (5)

Рис. 1. Расчетная схема
Нормальные напряжения σ 1 , σ 2 в стержнях и скорости их сечений υ 1 и υ2 удовлетворяют системе уравнений, составленной из уравнений движения и закона Гука в продифференцированной форме:
На ударяемом конце стержня x =0 имеет место условие g = —g 0 . (6)
Область движения от области покоя в рассматриваемой задаче, во всяком случае, до некоторого момента, определятся характеристикой x = a 2 t (рис. 2). Решение в области о < x < a2t (обозначим ее I) ищется в виде (4) методом характеристик. Передний фронт возмущения в стержне начинает распространяться как ударный. Условие сохранения количества движения на характеристике x = a 2 1 имеет вид [ g ] + a 2 P 2M = 0 • С учетом условия (5) это соотношение можно переписать как
дG 1 д x
du
P i.1 +x q ; д t
8g du
- = E1 д t д x
8g? 5u7
—2 = P 2 2
дx д t
— x q ;
дG^
2 = E 2
дtд
;
fLN S
Величина X = sign | P 1 - ° 2 J в случае движения, а в случае покоя принимаем любое значение в пределах от -1 до +1. Системы уравнений (1) и (2) можно свести к
неоднородным волновым уравнениям.
2ди дu_ Xq a1 _ т _ т = дx 2 д t2 P1
2 д и д и _ X q a2 —5---У =■ дx2 д t2P
g + a 2 P 2 p = 0 при x = a 2 t
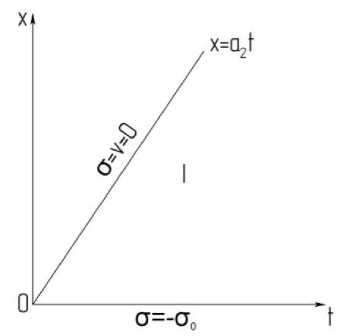
Рис. 2. Область движения от точки покоя
Для того, чтобы найти общее решение неоднородного волнового уравнения, необходимо использовать соотношения вдоль характеристик этого уравнения. Характеристиками неоднородных волновых уравнений являются линии
Из условий (5) и (7) находим решение в области I для второго стержня, учитывая, что χ=-1
qt u = "^ + u0 2P2
dx = ± ad „ dx = ± a^dt
1 и 2
qx g =
-g 0
, где
n - G0 u0 =---- a 2P2
По этим линиям распространяется разрыв решения. Вдоль характеристик имеют место соотношения ± dG + a 1 P 1 d u + a»qdt = 0 Для первого стержня и ± d G+ a 2 p 2 d u + a 2 x qdt = 0 для второго стержня. Решение задачи Коши ищется в виде: для первого стержня:
U 1 = —~—+ a 1 f ( a ^ t — x ) + a 1 ^ ( a 1 1 + x ) 2P 1 (3)
g 1 =X qx — E 1 f ( a1t — x ) + Е 1 ф ( a1t + x )
для второго стержня:
U 2 =---—+ a 2 f ( a 2 1 — x ) + a 2 ф ( a 2 1 + x )
2P 2 (4)
Для первого стержня σ 1 и υ 1 удовлетворяют системе (1). В момент t=0 все сечения стержня, в том числе и x =0, считаем неподвижными и ненапряженными, т.е.
g = u = 0 при t = 0 и x > 0 (9)
g = 0 при x = 0 (10)
Область движения от области покоя в этом случае отделяется фронтом x=a 2 t , который не является характеристикой (1) (рис. 3).
Решение в областях a1t < x < a 2 1 ( Ia ) и 0 < x < a1t ( I g) ищется в виде (3) методом характеристик. Условие сохранения количества движения на фронте x=a 2 1 распадается на два условия [ g ] = 0 и [ и ] = 0 • Эти два соотношения можно переписать в виде
[ст ]± a 2 pjp ] = 0
скорости выравниваются.
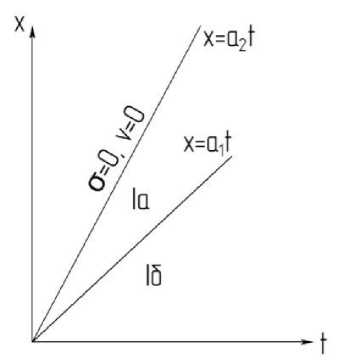
Рис. 3. Схема поиска решения
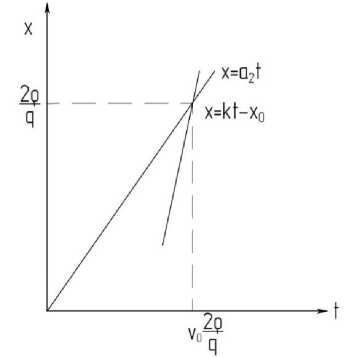
Рис. 4. Поиск точки пересечения линий
Из условий (9) и (11) находим решение в области
I a для первого стержня, считая х=-1
и = qa 2 ( a 2 ' - х 1
Р 1 ( а 2 - а 1 )
а =- q^ ( а 2 t - х )
а 2 - а 1 (12а)
Рассмотрим прямую х = kt - х о . Скорость и о имеет тот же знак, что и п о . Это означает, что x о >О всегда, т.к. a 2 > a 1 . Можно показать, что a 2 < к .
2 р 2 а 2 +р 1 ( а 2 - а 1 ) > а
2 р 2 а 2 2
При x=a 2 1 условие количества движения с учетом решения в области I a дает:
[а]+ а1р1[и] = 0 или
qa 1 ( a 2 t - х ) qa 2 а ( a 2 t - х )
а +---2---2— + а 1 р 1 и 2---2— = 0
а 2 — а 1 а 2 — а 1
Из условий (10) и (13) находим решение в области I б . В этой области х=-1.
q a2t р1 а1 + а 1
qa1t а1 + а -2
(12б)
Решения (8) и (12) справедливы в области I до тех пор, пока U 1 < U 2 , т.е. х=-1. Найдем линию, на которой скорости обоих стержней выравниваются. При а ^ < х < а 2 t
х =
2 р 2 а 2 +Р 1 ( а 2 - а 1 ) t
2 р 2 а 2
—
ЭД а 2 - а 1
q a 2
Обозначим
2 р 2 а 2 + р 1 ( а 2 - а 12 ) = 7 .
2Р2 а -2’ и0р1 а2 - а1_
--= хо ’ х = kt — хо qa при о < х < a1t
* = t * = 2 и о р 2 р 1 ( а 1 + а 2 )
q ( 2 р 2 а 2 +р 1 ( а 1 + а 2 ))
2 р 2 а 2 + р 1 ( а 2 - а 12 ) > 2 р 2 а 2 р 1 ( а 2 - а 1 2 ) > о.
б)
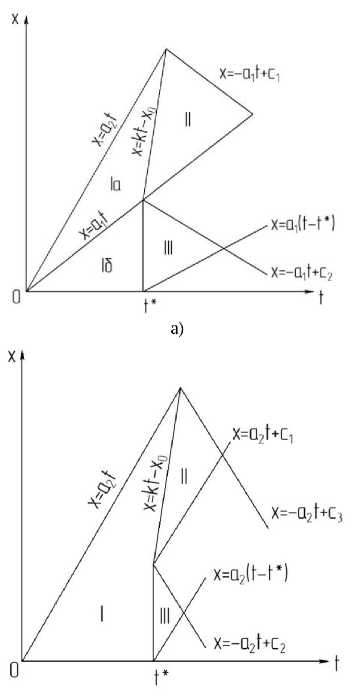
Рис. 5. Геометрическая интерпретация характеристик
Согласно рис. 4 на линии
х = kt - х о
*
t = t
при
а 1 1 < х < а 2 1 о < х < а 1 1
Прямые x=kt - x о и t = t * пересекутся в точке х = а ^*. Это означает, что ломаная линия (14) является
непрерывной. На линии (14) скорости движения сечений u i и U 2 выравниваются, но каким будет дальнейшее движение - неизвестно. Для того чтобы выяснить характер дальнейшего движения, необходимо рассмотреть задачи Коши для первого и второго стержней в областях, образованных соответствующими характеристиками (рис. 5а, б). Периодически будем обращаться к уравнениям математической физики [25-28].
Для первого стержня в области II ищется решение системы (1) в виде (3). На границе области II x=kt -xо выполнены условия u = q- 2 a2 2 ((a 2 — k > + xо) pi a2 — ai
G = — q 2 1 2 (( a 2 — к ) t + x о )
a 2 — a 1 (15)
Также решая методом характеристик, находим решение в области III
in 2x +1 ( *)
u2 = -^q ( t — t ) +u
III qx
G 2 = T
— G 0
После того, как найдены решения для обоих стержней в областях II и III , можно определить значение x в этих областях. Очевидно, что в дальнейшем стержни будут двигаться как единое целое, при усло-
вии, что 1х1<1
Запишем систему уравнений для совместного движения стержней. Для этого сложим систему уравнений (1) с системой (2). При этом необходимо учесть, что U 1 =U 2 . Обозначим 0 1 + 0 2 = о Нормальное напряже
Решаем эту задачу методом характеристик. В области II получаем решение:
ние о в составном стержне и скорость его сечения и, удовлетворяет системе уравнений, состоящей из урав-
нения движения и закона Гука:
u I
( x + 1 ) qk ( kt — x — x 0 ) p,W — к 2 )
qa 2 ( x — a 2 1 ) Pl( a 2 — ai )
5g / \5о — = ( р 1 + p2 Нг d x о t
II _ ( x + 1 ) qa 1 2 ( kt — x — x 0 ) qa 2 ( x — a 2 1 )
1 = 2,2 2
a i — к a 2 — a i
dG = ( E, + E )du d t V d x
Обозначим p= p 1 + p 2 , E= E 1 + E 2. Продольные упругие волны при совместном движении стержней бу-
В области III для системы (1) решение ищется в виде (3). На границе области III 0 $ x $ a 1 t , t=t* выполнены условия
дут распространяться в составном стержне со скоро-
стью a
E i + EE 2 р 1 +р 2
*
и = и
2 u 0 a 2 р 2 _____
2 P 2 a 2 +P 1 ( a 1 + a 2 )
g = — q
a1x ai + a 2
Найдем характеристики и соотношения вдоль них для системы (22). Характеристиками являются линии dx =± adt . Соотношения вдоль этих характеристик d G = ± a р d и . Решение системы (23) будем искать в
Также решая методом характеристик, находим решение в области III
u f11 = q lx +
P i ( a i + a 2
*
l ( t — t ) + и
G 111 =— q a 1
a i + a 2 .
Для второго стержня в области II ищется решение системы (2) в виде (4). На границе области II ( x = kt - x о ) выполнены условия
qt u , ■ u0
2 P 2
qkt g =--
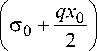
виде
G i = f i ( at + x ) + Ф 1 ( at — x ) +G 1o ( x )
G 2 = f 2 ( at + x ) + Ф 2 ( at — x ) + G 2o ( x ) u = f з ( at + x ) +Ф э ( at — x ) + At , где mo ( x ); O 2o ( x ) - граничные условия.
Неоднородность в решениях появляется за счет того, что необходимо разделить напряжения в первом и втором стержнях. Для системы (22) решение имеет вид:
G i = E i f ( at + x ) + Е 1 ф ( at — x ) + g^( x )
G 2 = E 2 f ( at + x ) + E 2 ф( at — x ) +G 20 ( x )
_ x (23)
u = af ( at + x ) — a ф ( at — x ) +
Решая эту задачу методом характеристик в области II ,
£ | d G ia ( x ) + d G 20 ( x ) р ^ dx dx
получим
„и (x+i)qk(x—kt+xо) qt , „ и2 =----ПЧ— + ио р2 (a2 — к )
II _ (x + i)qa2 (x — kt + x0)
G 2 = 2 ,2 7 — G 0.
a 2 — k2
В области III для системы (2) решение ищется в виде (4). На границе области III 0 $ x $ a 1 1 , t=t * выполне-
Решения будем искать в областях, образованных характеристиками dx =± adt . (рис. 6). Решения в областях II , III и IV будем искать в виде (24). В области II решаем систему (22), при условии, что на её границе x = kt - x 0 :
G 10 =
qa i ( a 2 1 — x )
22 a 2 — a i
ны условия
*
u = u
qx 2
— G 0
qx g20 =y—g0
qt u = —---+ u0.
2 P 2
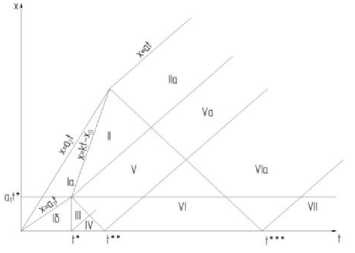
Рис. 6. Геометрическая интерпретация поиска решений
В области IV решаем задачу Коши для системы
(23). Решение ищется с +с2 с2 = —с0 (или 1 2
при x = a ( t — t * ) : ст =
в виде (24). При x =0 ^j = 0,
—
с 0 ), qax a ( t — t *)
ax + a 2
^ 20
qa ( t — t *)
--^ i
*
U 0 = и
*
t — t q a2 — ax
p 2 a 2 + a ,
На характеристике x=a(t – t*) для нахождения
x + x 0
В этом случае t = —-— и значения аю, 020 и и на грани це перепишутся так:
решения используем закон сохранения количества движения [с] + a p [ u ] = 0 • С учетом условий (29) он перепишется следующим образом:
с — ( сю + ^ 20 ) + a ри — a pU 0 = 0
с 10 = +
qa 1 (( k — a 2 ) x — a 2 x 0 )
k ( a 2
—
a 1 2
)
Из условий (28) и (29) находим решение в области IV . Оно будет иметь вид
qx с20 = ~ —с0
q x + x u = —--- 0 + Un
2p 2 k
Решая (23) при условии (24), находим области. Оно будет иметь вид:
f J_ + q +
(24) решение во II
t
U = U +-
—
A
с 1 =
E 1 ( kt — x — x 0 ) 2 p 2 2 p
2 7 2
a — k
+
V
qa ^ ( k — a 2 )
+
с 2 =
U = —
с 1 =
qa i x
a 1 + a 2
qx с2 = —
2 2
—
с 0
, *
t q a 2 — a 1
p 2 a 2 + a 1
Р k ( a 2
^O FiJ
qa 1 (( k - a 2 ) x - a 2 x 0 ) k ( a 2 — a 1 )
E 2 ( kt — x — x 0 )
f — + q + 2 Р 2 2 p
A
22 a — k
k ( kt — x —
qa 12 ( k — a 2 ) CP k t a TT) J
-q -+ q +
x 0 ) 2 P 2 2 P
22 a — k
qa 12 ( k — a 2 )
V+P ka F — a ?) J
—
qx
+ Ч — с 0
qt
2--+ U 0
2p 2
Значение χ в области II по модулю меньше 1. Это можно проверить, подставив σ 1 и υ из (26) в систему уравнений (1) или σ2 и υ в систему (2). В области III решаем систему (22), при условии, что на её границе 0 ≤ x ≤ a 1 t , t=t *
qa x с10 =--—
a i + a 2
qx
, с 2 0 = — — с 0 ; U = U * .
Решение в области III имеет вид:
с 1 =
—
qa i x
a 1 + a 2
qx с2 = ~ — с0
t
U = U +
*
— t
q a 2
—
a 1
p 2 a 2 + a 1
Значение χ в области III также по модулю меньше 1.
Очевидно, что в области IV |χ|<1.
Во всех последующих областях найти решение системы (22) в виде (23) не удастся, т.к. в этих областях решается задача Гурса [25, 26]. Поэтому решение будем искать в виде
с] + с 2 = Ef ( at + x ) + E ф ( at — x )
и = af ( at + x ) — a ф ( at — x )
Необходимо заметить, что нужно разделять σ 10 , σ 20 для 0 ≤ x ≤ a 1 t* и x > a 1 t *. В первом случае нужно брать значения σ 10 , σ 20 на прямой t = t * при 0 ≤ x ≤ a 1 t, а во вто-
ром
–
значения на прямой x = kt – x 0 . В точке
I t = u 0 2 —, a 2 t 1 передний фронт отходит от линии x =
V q J a2t и движется с некоторой заранее неизвестной скоростью bi. Если b ^ a, то решение в области IIa будет тривиальным. Это означает, что область образована ха-
рактеристиками
x = at + ( a 2 — a ) 2 u 0 — q
и
x = — at + ( a 2 + a ) 2 u 0 — .
q
Вдоль характеристики x = at + ... выполнено условие
с = и = 0.
При x = - at + c нам известны σ 1 , σ 2 и υ из (25). Используем эти условия в области IIa при решении задачи Гурса. Решение будет иметь следующий вид:
f q^ + qk + ^
с =
E ( at — x ) 2 р 2 2 р
2 a 2 ( a — k ) + qa 2 ( k — a 2 )
V
p( a 2 — a 12 )
с 1 = —
—
+ E U 0 X — с 0
E 2 qa 2 (( k — a 2 ) x — a 2 x 0 )
E
k ( a 1 — a 2 )
—
E 1 qx + E 1 f E ( at — x ) ( ..X E
E 2 E V 2 a 2 ( a — k ) ') 10
E 1 qx
On —---+
2 E 2
E 2 qa 1 (( k - a 2 ) x — a 2 x 0 )
E
k ( a 1 — a 2 )
+
c 1 =
—
E 2 Ча 1 (( k — а 2 ) x — a 2 x 0 )
E
E 2 I E ( at — x ) / AI „ .
+ -fI E 2 u 0 ^ — c 0
E V 2 a 2 ( a — k ) J
k ( a 1 — a 2 )
—
—
E 1 qx
E 2
E 1 **
— 7v(... ) + E 1 c V
E
u— ( at — x )
2 a ( a + k )
f -О- + qk +
2 P 2 2 p
A
q a 1 2 ( k — a 2 )
V+^( a r;H J
—
Л , a2p2 a U0^ +--U0, ap
E 1 qx
On —+
2 E 2
E 2 да у (( k — a 2 ) x — a 2 x 0 )
E
k ( a 1 — a 2 )
—
где
\ p2 ( a + a 2 ) k
Л —2Г
V a ( a — k )
—
p 1 ( a 2 a 2 ( a 2
—
—
a, I
—14 lx k 2) J
E **
— — ( ... ) + E 2 c V —
E
c 0
X
f 1
V
- ! 1 ! a 12 ( k — a 2 )
2 p 2 2 p p k ( a 2 — a 1 )
—
+
В области VI решаем задачу Коши. При x — — at + ( a + a ,) t * используем условие (35) и закон сохранения количества движения [ c ] + a p [ u ] = 0. При x =0 считаем, что σ 1 =0, σ 2 =- σ 0 . Находим, что в области VI решение системы уравнений (22) имеет вид:
p2 I a + aT
+ — —2—
E
a 1 ( k — a 2 )( a + a 2 ) k ( a 2 — a 1 )
—
E 1
E ■ k
c 1 +^ 2 =
—
qx
a p k a1 ( k — a 2 )
a + k V 2 P 2 2
2 a 2
—
a1 J
—
c 0
В области V решаем задачу Гурса. На характеристиках x — — at + ( a + ax ) t * используем условие (31), x — at — ( a — axt *) - условие (26). Решение системы уравнений (23) в области V имеет вид
и — —
**
где
при
при
O 1 + O 2 =
q ( at + x ) | a p k a 1 ( k — a 2 )
2 ( a + k ) V 2 p 2 2
a 22
a 12
q ( at — x ) a 2 — a 1
** и v
**
+ E c V
O0
a 2 + a 1
_ aq ( at + x ) | a p k a 1 ( k — a 2 )
— — 2 E ( a + k ) I 2 p 2 — 2
qa ( at — x ) a 2 — a 1
4 E
a 2 + a 1
— - —
a 2 2
—
a 1 2
+
—
**
a и у + U 0 ,
qt
p ( a + k ) l 2 p 2 2
a p k a 1 ( k — a 2 )
----— --------
a 22
—
2 a 1
**
+ U yi + u 0 ,
**
где u VI = a c V
* при x < a ^
c 1 — —
—
**
a » v
E 2 qa 1 x
E a 1 + a 2
—
E 1 qx E 1 qx
E "2" + E a + k
E 1 qx E 2 qa 1 x E 2 qx
On —---1----1--- I ... I — On
E 2 E a 1 + a 2 E a + k v .
*
при x > a ^
° 1 — —
E 2 q ai (( k — a 2 ) x — a 2 x 0 )
E
k ( a2 — a 2 )
—
= uQ p 1l
2 Ea
( a 2 — a ? ) f - 2( a + k ) V
a p a
—— + — +
a i2 ( a + a 2 )
—
2 P 2
a 22
—
a 12
+
E 1 qx E 1 qx
E 2 + E a + k
**
+ qat a 2 — a 1 и
4 E a 2 + a 1 2 a
E 1 qx
On —+
2 E 2
E 2 qa i (( k — a 2 ) x — a 2 x 0 ) qx
E
k ( a 2 — a 2 )
+
**
c v =
—
u 0 p 1 ( a 2 — a 12 ) a p 2 Ea 2 ( a + k ) V 2p 2
*
1 qat a 2 — a 1
—
* qt
4 E a 2 + a 1 2 a P 2
*
x < a ^
° 1 — —
E 2 qa 1 x
—
—
E 1
E
a
+ — +
E 1 qx
E a 1 + a 2 f q ( a t + x ) / x
2 ( a + k )(-) + q ( a t — x ) a 2
V
E 1 qx
On —---+
2 E 2
E 2 E
*
x > a ^
E
—
E 2 qa 1 x
E a 1 + a 2
A
a 1
a 2 + a 1 J
f q ( at + x ) / v 2 ( a + k )( ... )
+ q ( at — x ) a 2
A
a 1
V
a 2 + a 1 j
a y ( a + a 2 )
a 2 2
—
2 a 1
+
E 2 qx
+ 77(--- )_O 0 -
E a + k
В области Va решаем задачу Гурса на характеристиках x — at — ( a — axt * ) используем условие (36)
x — — at + (a 2 + a )2^0 ^2- q - условие (37).
Решая эту задачу в области Va для системы (23) находим
—
O 1
( \ q a 7 — a i „ **
+ O 2 — — ( at — x )7 + E c Va
4 a 2 + a 1
+ O 0
**
+ E 1 c V
+ E 2 c V
c 0
где
c 1
**
u — ( at — x ) qaa 2Z a 1 4 E a 2 + a 1
**
cVa — uVa —
**
^ V
—
—
**
a u Va
—
u 0
4 ,
—
** uV
E 2 q a 2 (( k — a 2 ) x — a 2 x 0 )
E
k ( a 1 — a 2 )
—
E 1 qx E 2
E 1 **
+ — ( — ( at — x )- ) + E 1 c Va E
_ Ei qx E 2 qa 1 (( к - a 2 ) x - a 2 x о )
2 E 2 E k ( a 2 - a 2 )
+ -2- (-( at - x ).. ) + E 2 ° a - ° q .
E
В области VIa также решаем задачу Гурса на характеристиках x = at - ( a + a ) t * используем условие (36)
x = - at + (a 2 + a )2uq — q - условие (37).
Решая задачу Гурса в области VIa, находим решение для системы (23):
° 1 + ° 2 =
( aSL _ k _)
q(at - x) 2p2
-
2 - a 2 ( k - a 2 )
v a 2 - a 12
**
E и и ° о U q
*
при x < a 1 1
E 2 qa 1 x E 1 qx
° =------
-
1 E a 1 + a 2 E 2
E 1 qx E 2 qa 1 x
°2 =---1---
2 E 2 E a 1 + a 2
-° o
*
при x > a 1 t
_ E 2 qa2 (( k - a 2 ) x - a 2 x 0 ) E 1 qx
°=- E k ( a 2 - a 2 ) E T
E 1 qx E 2 qa 12 (( k - a 2 ) x - a 2 x 0 )
° 2 = E T + E k ( a 2 - a 2 ) ° 0 .
Обсуждение результатов решения. Рассмотрев одиннадцать областей и найдя в них решения, мы нашли решения во всем рассматриваемом квадранте x≥0, t≥0. Качественные выводы из полученного реше- ния задачи можно получить, рассмотрев зависимость
u( t , x = q ) и ° ( x , t ) при фиксированном t (рис. 7,
8а,б).
2 a 2 2 a p
q ( at - x ) ( a p _ k _ a 2 ( k - a 2 ) 2 a p V 2 P 2 2 a 2 - a 12 ,
**
+ u VI ! °0 ! u0
-
2 2 a p 2
*
при x < a i t
E 2 qa 1 x E 1 qx
° i =---- +
E ax + a2 E 2
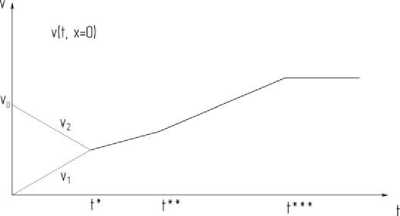
Рис. 7. Зависимость скорости от времени
+ E 1 ( ... ) + E 1 ° 0 - E^
E E 2 2 a p
E qx E qa x
°2 = +
E 2 E ax + a2
+
E 2 ( )_ E 1 ° 0 E 2 ° 0 E 2 u o
E E 2 E 2 a p
*
при x > a i t
_ _ E 2 qa 2 (( k - a 2 ) x - a 2 x 0 )
E k ( a 2 - a 2 )
E qx E 2
E 1 ( ). E 1 ° o
E ... E 2
E qx ° =---+
E 2
E 2 qa 2 (( k - a 2 ) x - a 2 x 0 )
E k ( a 12 - a 2 )
E 1 u o
2 a p
E
+ 2 ( ... ) +
E
E 1 ° 0 E 2 ° o E 2 U q
E 2 E 2 a p
Найдем решение в области VII. Здесь решается
задача Коши. При x = at - (a2 + a)2u0 22 используется q условие (39). При x=0 считаем, что σ1=0, σ2=- σ0. Таким образом, в области VII решение системы уравнений (23) имеет вид:
°1 +° 2 =-° o
u =
a 2 p 2
u 0 a p
До момента t = t* скорость υ1 возрастает от нуля до некоторого значения υ*, а скорость υ2 убывает от некоторого значения υ0 до того же значения υ*. Затем скорость совместного движения стержней возрастает по линейному закону. В момент времени t = t*** ско- a2p2u0 _ рость принимает постоянное значение . . В фиксированный момент времени t, такой что t < t*, напряжение в первом стержне в области 0 < x < axt убывает по линейному закону от нуля до некоторого значения, а затем при axt < x < a2t значение 01 возрастает по линейному закону до нуля.
При x > a2t значение 0 1 остается равным нулю. Во втором стержне напряжение возрастает от значения -σ 0 до некоторого значения σ 2 при x = a 2 t , при x > a 2 t значение напряжения равно нулю. При x = a 2 t происходит скачек в значении напряжения для второго стержня, т.к. фронт x = a 2 t для него является ударным.
В фиксированный момент времени t, такой что t > t***, напряжения в первом стержне убывают по линейному закону от нуля до некоторого значения σ1 при x = a1t* При x > a1t напряжение σ1 возрастает до нуля по линейному закону и при значении напряжения в первом стержне остается равным нулю. Напряжение во втором стержне возрастает по линейному закону от значения -00 до нуля при x = at + 2u0 ^^ (a2 - a1) и при q x > at+ 2uq “(a2 - a1) оно остается равным нулю.
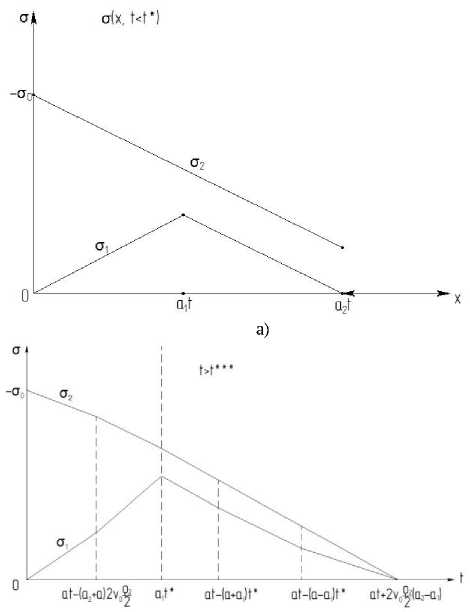
б)
Рис. 8. Изменение напряжений: а) от координаты, б) от времени
Вывод: из предложенного грофоаналитическо-го решения задачи можно получить соотношения для напряжений и скоростей в составных стержнях и материалах.
Список литературы Динамическая модель распространения волн от ударного импульса в составном стержне с учетом трения
- Сосенушкин, Е.Н. Развитие систем пластического деформирования//Вестник МГТУ «Станкин». 2010. №1. С. 30-38.
- Grigor'ev, S.N. Complex surface modification of carbide tool by Nb plus Hf plus Ti alloying followed by hard facing (Ti plus Al)N/S.N. Grigor'ev, S.V. Fedorov, M.D. Pavlov et al.//Journal of Friction and Wear. 2013. T. 34, № 1. P. 14-18.
- Кобелев, А.Г. Технология слоистых металлов/А.Г. Кобелев, И.Н. Потапов, Е.В. Кузнецов. -М.: Металлургия, 1991. 248 с.
- Ponomarev, A.S. Effect of process features of pressure treatment on the microstructure and quality of parts of pipeline fittings from higt-strength cast iron/A.S. Ponomarev, E.N. Sosenushkin, V.N. Klimov//Metal Science and Heat Treatment. 2012. T.54. №1-2. P. 22-27.
- Adaskin, A.M. Use of the effect of stress relaxation for changing the shape of articles from nonplastic steels and alloys//Metal Science and Heat Treatment. 2012. T. 54, № 1-2. P. 47-51.
- Емельянов, В.В. Технические требования и режимы прокатки биметаллических листов для изготовления из них изделий способом ротационной вытяжки/В.В. Емельянов, Е.Н. Сосенушкин//Заготовительные производства в машиностроении. №7. 2015. С. 39-42.
- Никитин, Л.В. Динамика упругих стержней с внешним сухим трением//Успехи механики. 1988. Т. 11. Вып. 4. С.53-106.
- Никитин, Л.В. Распространение волн в упругом стержне при наличии сухого трения//Инженерный журнал. МТТ, 1963. Т. 3. Вып. 1. С. 154-157.
- Никитин, Л.В. Удар жестким телом по упругому стержню с внешним сухим трением//Инженерный журнал, МТТ, 1967. №2. С. 166-170.
- Nikitin, L. Effects of dry friction оп the formation of seismic pulses/L. Nikitin, A. Khamraev, E. Yanovskaya//Physics of the Earth and Planetary Interiors, 50(1988) 26-31. Elsevier Science Publishers В.V. -Amsterdam (Printed in the Netherlands). -С. 21-38
- Елисеева, Ю.В. Математическое моделирование процессов, явлений и структур в сложных системах/Ю.В. Елисеева, О.А. Казаков, Л.А. Уварова и др.//Вестник МГТУ «Станкин». 2008. №1. С.44-59.
- Уварова, Л.А. Математическое моделирование процессов переноса электромагнитных волн в нелинейных средах/Л.А. Уварова, К.А. Будный, Е.М. Красикова//Вестник МГТУ «Станкин». 2010. №4. С. 110-115.
- Уварова, Л.А. Моделирование переноса частиц в цилиндрических системах/Л.А. Уварова, Л.В. Плетнев//Вестник МГТУ «Станкин». 2011. №4, С. 63-66.
- Яновская, Е.А. К задаче о колебаниях мембраны, с сосредоточенными массами//Сб. «Численное моделирование в задачах механики». -М.: Изд-во Московского университета, 1991. С. 43-47.
- Яновская, Е.А. Колебания мембраны под действием распределенных нагрузок//Сб. «Аналитические и экспериментальные методы в механике». -М.: Изд-во Московского университета, 1995. С. 66-70.
- Яновская, Е.А. Колебания прямоугольной пластины под действием сосредоточенных нагрузок//Фундаментальные физико-математические проблемы и моделирование технико-технологических систем. Выпуск 10. -М.: Изд-во «Янус-К», 2007. С. 28-29.
- Дмитриев, А.М. Разработка технологии производства корпуса гидроцилиндра из железного порошка/А.М. Дмитриев, Н.В. Коробова, М.Д. Петров//Вестник МГТУ «Станкин». 2014. №1(28). С. 54-58.
- Сосенушкин, Е.Н. Технологические пpоцессы пpоизводства изделий из поpошковых матеpиалов. Учебное пособие с гpифом УМО АМ. -М.: МГТУ «СТАНКИН», 1995. 96 с.
- Сосенушкин, Е.Н. Технологические процессы и оснастка для переработки пластмасс и порошков. Часть 2. Технологические процессы и оснастка для переработки порошковых материалов. Учебное пособие с гpифом УМО АМ. -М.: МГТУ «Станкин», 2012. 173 с.
- Sosenushkin, E.N. The Parameters of the Stress State in the Operations of Plastic Deformation/E.N. Sosenushkin, V.A. Kadymov, E.A. Yanovskaya et al.//Key Engineering Materials Submitted: 2015-09-16. ISSN: 1662-9795, Vol. 684, pp 57-66, doi:10.4028/www.scientific.net/KEM.684.57/Revised: 2015-11-13. Accepted: 2015-11-13. © 2016 Trans Tech Publications, Switzerland Online: 2016-02-18.
- Sosenushkin, E.N. Stress state parameters of the plastic forming operations/E.N. Sosenushkin, V.A. Kadymov, E.A. Yanovskaya et al.//Materials of the IX International Research and Practice Conference on European Science and Technology. V2. December 24-25. 2014. Munich, Germany. P.451-459.
- Сосенушкин, Е.Н. Исследование влияния дефекта структуры на эксплуатационные характеристики чугунных деталей/Е.Н. Сосенушкин, Л.С.Французова//Сб. научных трудов «Проблемы формирования и развития современного технологического общества». -Егорьевск: ЕТИ ГОУ МГТУ «СТАНКИН», 2005. С. 111-113.
- Котелкин, А.В. Оценка технического состояния сварных соединений по уровню остаточных напряжений/А.В. Котелкин, А.Д.Звонков, Е.Н. Сосенушкин и др.//Заготовительные производства в машиностроении. 2015. №7. С. 10-14.
- Бушенин, Н.В. Курс теоретической механики т. 2/Н.В. Бушенин, А.Л. Лунец, Д.Р. Меркин. -М.: Наука, 1979. С. 50-53.
- Арсенин, В.Я. Методы математической физики и специальные функции. -М.: Наука, 1984. 384 с.
- Владимиров, В.С. Уравнения математической физики. -М.: Наука, 1971. 512 с.
- Елисеева, Ю.В. Один метод вычисления собственных значений дискретных задач Штурма-Лиувилля высших порядков/Ю.В. Елисеева, А.А. Бондаренко//Вестник МГТУ «Станкин».2011. №1. С. 95-102.
- Иванова, О.К. Исследования в области фундаментальной и прикладной математики. Слабая обобщенная локализация для кратных рядов Фурье/О.К. Иванова, А.В. Боголюбов, А.В. Зарелуа и др.//Вестник МГТУ «СТАНКИН», 2008. №2. С.66-74.


