Динамическая устойчивость адаптивной панели крыла экраноплана

При разработке систем низковысотных ЛА возникает ряд задач по исследованию характеристик морского волнения, для решения которых требуются специальные методы. Это объясняется преимущественно следующими обстоятельствами. Возможные авиационные скорости движения ЛА на порядок превышаютскорости водоиз-мещающих морских объектов, приводят к существенным особенностям формирования спектра морского волнения в движущейся, связанной с объектом системе коор-динат[1].

Установлено [2], что при движении над синусоидальным волновым экраном кривые зависимостей гидродинамических характеристик крыла от времени изменяют-сянепо синусоидальному закону, апо закону, близкому к трохоидальному (рис. 1, 2), а также несимметричность этих кривых относительно вертикалей, проходящих через их максимумы, и их сдвиг по фазе относительно волн экрана [3]. Определено, что средние за период волны значения подъемной силы крыла над волновым экраном превышаютпо величине значения подъемной силы крыла при его движении над плоским экраном, расположенным на уровне средней линии волны экрана (рис. 3).

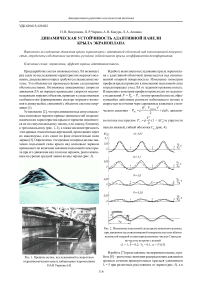
Рис. 1. Профиль волны, исследованный в скоростном гидродинамическом канале лаборатории гидромеханики

НАН Украины [4]

В работе выполнено исследование крыла экранопла-на с адаптивной оболочкой движущегося над взволнованной опорной поверхностью. Изменение геометрии профиля крыла приводитк изменению подъемной силы и предотвращает уход ЛА от заданного режима полета. Изменение геометрии профиля происходит из-за разности давлений F = P _вн - Р _∞ : во внутренней полости, образующийся действием разности набегающего потока и скоростью истечения через дренажные клапаны и стати-( V ∞ V дренаж )²

ческого давления – Р _вн =ρ      ^р     +ρ gh ; давлени-

V ²

ем потока под крылом Р∞ =ρ ∞ (1 + ΔСр) и упругости панели нижней, гибкой оболочки СEJ (рис. 4).

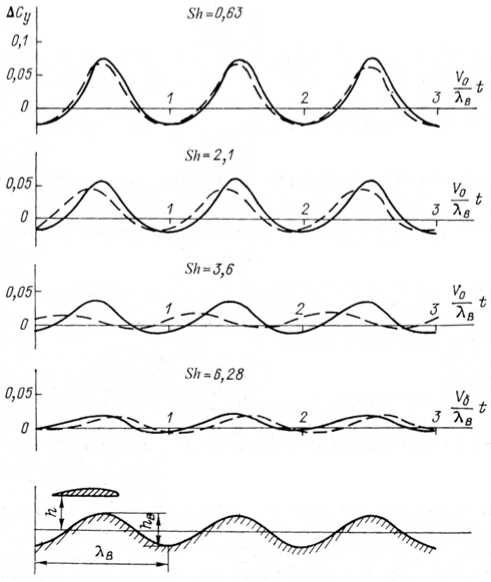
Рис. 2. Изменение подъемной силы крыла конечного размаха при движении над взволнованной поверхностью или вблизи волнистой твердой стенки при различных числах Струхаля по ч а стоте встречи с волной ( λ =1; h =0,2; ‘ h _в=0,1; α = 5^о) [5]

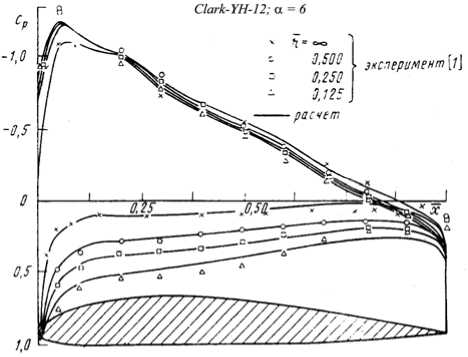
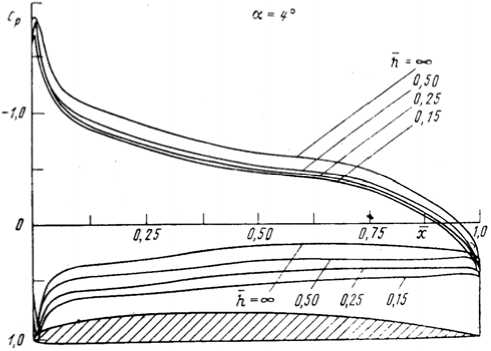
В работе [7] представлены экспериментальные, вра-боте [8] – расчетные значения распределения давления в среднем сечении прямоугольных крыльев удлинением λ = 5 при различных расстояниях от экрана (рис. 5), а в работе [9] приведена аппроксимация экспериментальных зависимостей изменения давления ΔС серии профилей (CLARK-YH, CLARK-Y, NACA, ЦАГИрсерииВ) вдиапа-зоне относительной высоты h = 0,1–1 и угла атаки α =4–14o:

Δ С =0,32634+0,00961 α – –0,55582 h 0 ^р ,02225 α h –0,001 α ²+0,33539 h ².

Сведения из [7–9] использованы в работе для определения величин и зон приложения нагрузок и сил на панель адаптивного крыла экраноплана [10].

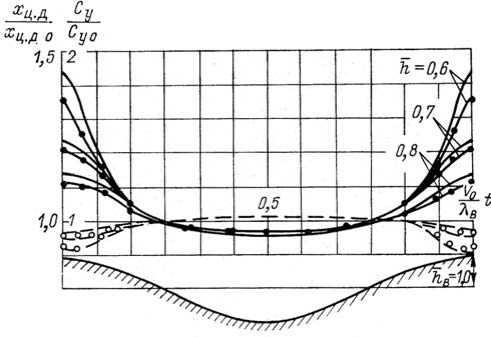
Рис. 3. Результаты расчетов подъемной силы (1) и положения центра давления (2) крыла с удлинением λ = 2 при Sh = 0,314 и движении вблизи волнистой твердой стенки. Кривые – расчетные данные, точки – экспериментальные [6]

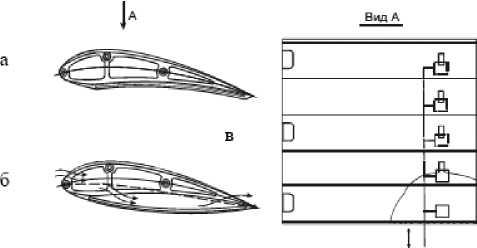
Рис. 4. Схема крыла экраноплана [6]

В настоящей работе предлагается метод оценки динамической устойчивости конструкции адаптивного крыла [10], движущегося над взволнованной поверхностью по критериям собственных частот конструкции и определения зон резонансных частот.

Расчетную схему крыла определяем как двухопорную балку с шарнирной и скользящей опорами, находящуюся под действием распределенного статического давления внутри крыла и вибрационной нагрузки, изменяющейся по трохоидальному закону, со стороны опорной поверхности (рис. 6).

Динамический расчетпанели крыла на действие возмущающей силы и колебания выполняется для балки на двух опорах массой m0. Определим максимальные динамические напряжения при действии на балку равнодействующей распределенной воздушной нагрузки qв в точке с координатой хm; собственную частоту колебаний с учетом массы балки и сосредаточенной силы в точке; перемещение точки хm балки под действием возмущающей силы F(t), приложенной в этой точке.

б

Рис. 5. Распределение давления в среднем сечении прямоугольных крыльев удлинением λ = 5 при различных расстояниях от экрана: a –по данным [7]; б –по данным [8]

a )

m

б )

шишпншиШ/

PaiBt

x m

Lrb

<

L

Рис. 6. Схемы балки: а – схема нагружения; б – расчетная схема [11]

В расчетной схеме можно менять положение опор на балке ( L_RA и L_RB ) и координату точки приложения распределенной воздушной нагрузки х_m . Для панели задаются модуль Юнга Е и плотность ρ материала панели. Определяем площади поперечных сечений А ( х ), момент инерции J ( х ) и массу панели (балки) m ₀.

Для динамического расчета балки как системы с одной степенью свободы определяется коэффициент приведения массы в точку действия сосредоточенной силы х_m . Так как масса панели крыла распределена по длине, система имеет бесконечное число степеней свободы. Чтобы рассмотреть ее как систему с одной степенью свободы [8], распределенную массу заменяем массой, сосредоточенной в точке, и равной по величине равнодействующей воздушной нагрузки Р_q , а собственную частоту панели определим как для системы с сосредоточенной массой m+ k _пр m ₀.

При определении собственной частоты системы с учетом ее массы условием приведения массы является равенство кинетических энергий систем с распределенной Е _расп и сосредоточенной приведенной Е _соср массой:

_E dm ⋅ V ²     m ₀ dx ⋅ V ²

Eрасп =∫2=∫2l    , mL

E соср ⁼ k пр m 0 V 0 .

Приравнивая кинетические энергии Ерасп = Есоср, находим коэффициентприведения массы k= пр mV 0m0

Распределение скоростей по длине балки ( V /V ₀) неизвестно, поэтому примем гипотезу, что распределение скоростей пропорционально распределению перемещений по длине балки (гипотеза справедлива для достаточно жестких тел при сравнительно малых собственных частотах – до первой собственной частоты), тогда

V _≈ Δ

^V 0 ^Δ 0 ^.

Коэффициентприведения массы примет вид kпр

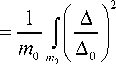
dm ,

где Δ и V – перемещение и скорость произвольной точки балки; Δ ₀ и V ₀ – перемещение и скорость приведения массы балки; dm = ρ A ( x ) dx .

Перемещения в этой формуле определяются с помощью интеграла Мора.

Изгибающие моменты для грузового М и единичного М 1 состояния балки, записанные с использованием булевых операторов условия пакета MathCad, выглядят следующим образом:

М ( F , R A , R B , x ) = R A ( x - L R _A )( x ≥ L R _A ) +

+ R_B ( x - L_RB )( x ≥ L_RB ) - F ( x - x_F )( x > x_F ), M 1( R_A , R_B , xx , x ) = R_A ( x - L_RA )( x ≥ L_RA ) + + R_B ( x - L_R )( x ≥ L_R ) - 1( x - xx )( x > xx ).(2)

Так как реакции опор на моментзаписи изгибающих моментов неизвестны, они внесены в список параметров функции. Для М 1 в списке параметров включена координата точки приложения единичной силы хх , а для М –сила F , так как по ходу расчета необходимо определить М отдействия различных сил, поэтому и опорные реакции определяются как функции от силы F . Из условия равновесия определяются опорные реакции панели в грузовом и единичном состоянии (рис. 7).

Коэффициент приведения массы kпр определяется перемещением в точке действия равнодействующей воздушной нагрузки (записан с использованием булевых операторов условия пакета MathCad)

Δ ( F ) = ∫

M ( F , R_A ( F ), R_B ( F ), x ) ⋅ M 1( R 1 _A ( x_m ), R 1 _B ( x_m ), x_m , x )

E ⋅ J ( x )

dx ,

и перемещениями в произвольной точке

L

_Δ ( xx ) _=∫ M ( F , R_A ( F ), R_B ( F ), x ) ⋅ M 1( R 1 _A ( xx ), R 1 _B ( xx ), xx , x ) dx ,   (4)

С учетом выражений (3) и (4) уравнение (1) примет вид

L kпр=m0⋅Δρ(F)2 ∫0A(x) ⋅ Δx(x)2dx.          (5)

Учетвнезапного приложения силы на панель крыла оценивается через максимальные динамические напряжения как и при ударе σmax.д = σmax. стат kд:

k = 1 + 1 + ^{2 h 1},

^{Д           Δ( F )} 1 + k ^{m 0 ,}

пр P qв где за h принимается расстояние от задней кромке крыла до опорной поверхности (см. рис. 2).

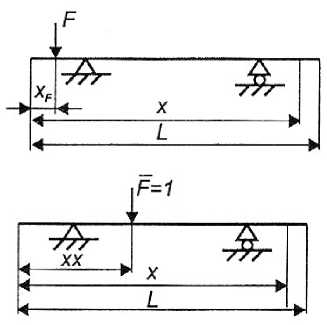
Рис. 7. Грузовое и единичное состояние балки при определении ее перемещений [10]

Максимальные динамические напряжения в панели могутбыть определены следующим образом:

W = b ^; σ

6 max.стат maxM

W ^;

σ max.Д ⁼ k Д ^⋅ σ max.стат ,

где b и δ – ширина и толщина рассчитываемой панели крыла.

Собственную частоту колебаний панели с распределенной массой m0 и сосредоточенной силой Рq6 , приложенной в сечении xm, найдем как k ω=            ,

P_{q в} + k _пр m ₀

где k = жесткость панели – величина, обратная пере- ^δ 11

мещению точки приложения сосредоточенной силы от

M12dS единичной силы δ11 =∑ ∫       .

По значению собственной (круговой) частоты ω определяем:

• –    частоту колебаний панели f = ^ω ;

2π

π

• –    период колебаний T = 2 .

ω

Вынужденные колебания панели под действием возмущающей силы можно определить через опытное значение коэффициента затухания h , значения относительного коэффициента затухания h / ω (по экспериментальным данным: для стальных конструкций h / ω ~ 0,02; для автомобильного амортизатора – 0,2; гидробуфера – > 1. В большинстве случаев – 0,01 <  h / ω < 0,3).

Уравнение колебательного движения системы (см. рис. 6) имеетвид

u ( t ) = A ⋅ e ^{- ht} sin( ω t + ε ) ,

∫ F ( τ ) e ^{- h ( t -τ)} sin ⎡_⎣ω ( t - τ ) ⎤_⎦ d τ . 0

u ( F , t ) =

( P + km ) ω q впр0

Это перемещение точки приведения масс в вертикальном направлении отдействия возмущающей силы F ( t ) (в работе принят трохоидальный закон изменения возму- C_y щающей силы [1]: F ( t ) = F ( r – h cos( vt )), F ₀ = P_q   ^y

0                               в _{Cy 0}

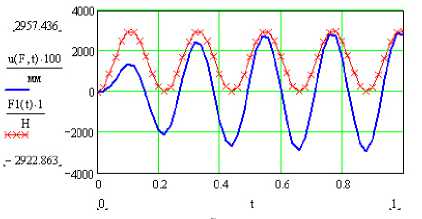
(см. рис. 3) [6], где v – частота действия возмущающей силы) (рис. 9) .

где A = u ₀ ²

( V ₀ + h ⋅ u ₀)

ω ²

2           ⎛uλ ⎞

, ε= arctg ⎜ ⁰        ⎟ ,

⎝ V ₀ + h ⋅ u ₀ ⎠

λ=ω⋅ 1-

h ⎞ ²

,

⎝ω⎠ где u0, V0 – начальные условия свободных колебаний (перемещение и скорость в момент действия импульса силы); ω – резонанс; λ – частота гармонических затухающих колебаний.

Свободные колебания панели крыла представлены на рис. 8.

.9.694.

-9.103.

пад

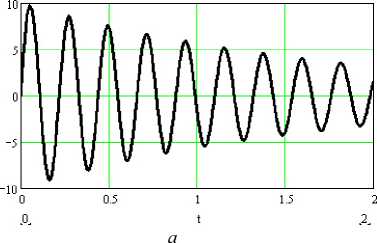
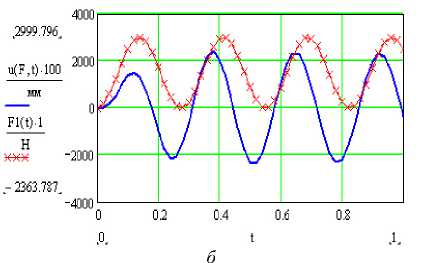
Рис. 9. Вынужденные колебания панели крыла с амортизатором: а – резонанс λ = ω ;

б – выход из резонанса λ =0,8 ω

Меняя выражения для возмущающей силы, можно получить графики перемещений для различных видов возмущающей силы (например, синусоидальный закон F ( t ) = F ₀ sin( vt )) (рис. 10).

7.598.

- 10

ul(t)

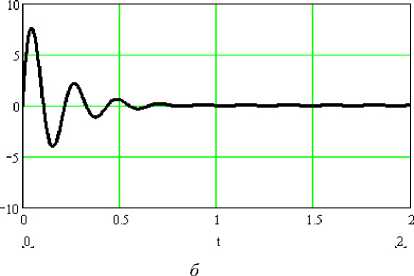
Рис. 8. Свободные колебания панели крыла: а – без амортизатора; б –с амортизатором

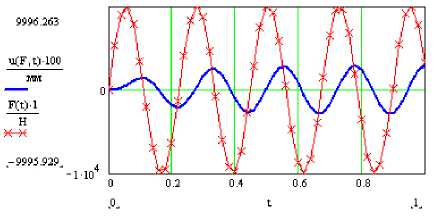
Например, (рис. 8, а , б ), для уменьшения времени затухания колебаний в конструкцию крыла в середине пролета введен амортизатор панели с h / ω = 0,2.

Для определения отклика панели на возмущающее действие силы использован интеграл Дюмеля для вынужденных затухающих колебаний:

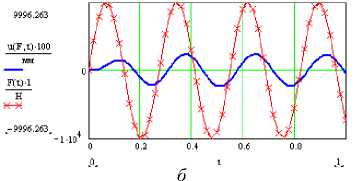
Рис. 10. Вынужденные колебания панели крыла с амортизатором: а – резонанс λ = ω ;

б – выход из резонанса λ =0,8 ω

Коэффициентдинамичности определяется как отношение максимальной амплитуды колебаний при резонансе к статическому перемещению от амплитуды вынужденной силы F ₀:

_{k =} u ( F , t _max)

^Д      Δ ( F 0 )^.

Максимальные динамические напряжения находятся по формулам (7), что и при внезапно приложенной нагрузке.

В результате выполненого исследования установлено: для компенсации вынужденных колебаний гибкой панели крыла необходимо введение в конструкцию демпфира (амортизатора) с относительным коэффициентом затухания h / ω ≥ 0,2 ( λ = 0,98 ω ), в месте наибольших прогибов панели; подбор жесткости колеблющейся системы необходимо осуществить так, чтобы частоты собственных колебаний панели были выше опасных вынужденных частот; увеличение коэффициента k жесткости панели достигается подкрепляющим действием продольного набора стрингеров, увеличивающего E ⋅ J изгибную жесткость панели (хотяив меньшей степени, чем поперечный набор, но дающий боль-шуючувствительность (гибкость) панели в реакции на внешнее возмущающее действие давления потока под крылом Р _∞ , изменяющимся по трохоидальному закону) для выполнения условия непопадания в резонанс λ = 0,8 ω , значение коэффициента затухания должно соответствовать величине h ≥ 0,6 ω собственной частоты системы, что требует наличия нескольких демпфирующих устройств.