Динамические характеристики машинных агрегатов

Повышение требований к точности размеров и формы деталей, обрабатываемых на металлорежущих станках, появление новых труднообрабатываемых материалов, а также широкое внедрение автоматизации технологических процессов и создание автоматических станков с системами управления и регулирования вызвало резкое увеличение роли динамических процессов в станках. При проектировании, изготовлении и эксплуатации станков все чаще возникает необходимость решения задач, связанных с динамикой явлений. В первую очередь это относится к обеспечению условий устойчивого движения инструмента и заготовки. Важнейшим условием, необходимым для определения динамической характеристики, является устойчивость элемента или системы. Расчет устойчивости и определение оптимальных параметров упругих механических систем являются одной из важнейших задач современной теории расчета и конструирования машин и механизмов. Недостаточный учет влияния сложной многокоординатной упругой системы машины на статическую и динамическую жесткость технологической системы отражается на качество ее результатов работы.

Целью такого расчета является установление размеров, формы, веса, рациональной компановки основных узлов и конструктивных элементов исследуемых устройств исходя

из условия устойчивости их динамической системы. Решение этих задач далее рассматривается в процессе конструирования агрегатных станков, в которых данные проблемы наиболее представлены. Судить об устойчивости данной системы, о поведении ее во время переходных процессов, о ее динамической точности, а также о необходимых изменениях параметров колебательной системы с целью получения области устойчивости в определенных пределах, наибольшую возможность дает метод, связанный с построением амплитудно-фазовой частотной характеристики.

Для расчета амплитудно-фазовой частотной характеристики упругая механическая система с той или иной степенью точности представляется в виде некоторой механической модели, состоящей из отдельных сосредоточенных жестких масс, соединенных упругими связями, заменяющими упругие стыки этих масс. Такое представление конструкции позволяет рассматривать ее как колебательную систему, состоящую из нескольких подвижных жестких масс, соединенных с неподвижными массами при помощи стыкового соединения. Каждый стык между этими массами заменены невесомыми пружинами. При колебаниях станка происходит взаимодействие динамических процесс-сов упругой системы станка с динамическими процессами резания. Расчетная схема упругой конструкции станка (несущей системы) приведена на рис. 1, на которой изображены в виде абсолютных твердых тел консоль, салазки, стол, деталь, поворотная головка и верхняя часть станины, центры масс которых сосредоточены в указанных точках.

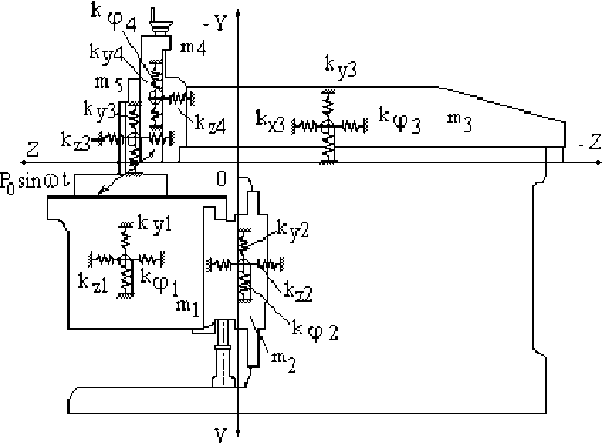
Рис. 1. Расчетная схема упругой конструкции станка

На рис. 1 обозначено: m1, m2, m3, m4, m5 – массы стола, поперечины, ползуна, вертикального суппорта, резцедержателя с резцом; kz1, kz2, kz3, kz4, kz5 – жесткости соответствующих стыков в направлении оси z; ky1, ky2, ky3, ky4, ky5 – то же в направлении оси y; kφ1, kφ2, kφ3, kφ4, kφ5 – крутильная жесткость стыков. Силу резания, лежащую в плоскости чертежа, примем направленной под углом α к горизонтали Р=Р0sin α. За обобщенные координаты приняты относительные перемещения масс, отсчитываемые от начала координат, расположенных в центре тяжести каждой массы и углы поворота масс относительно их центров тяжести. Конструкция, состоящая из одной подвижной массы, соединенной с другой неподвижной массой при помощи стыкового соединения, допускает 3 степени свободы.

Исследование колебательной системы рассмотрим на примере упругой системы стол-поперечина. За обобщенные координаты принимаем перемещения каждой массы относительно неподвижной системы координат и углы поворота каждой массы относительно их центров жесткости. Составляем выражения кинетической и потенциальной энергий и диссипативной функции. После соответствующего их дифференцирования и подстановки его результатов в уравнения Лагранжа получим следующие уравнения.

m i Z i + m i L i co^s(adTp + h zi z i + k zi z i - k zi z i ^{- p}₀c^os( a ^)siⁿ⁽ ro t) ;

m 2 Z 2 + m 2 L 2 c^os(a 2) &P 2 + h z2 z 2 + (k zi + z z2 )z 2 - k zi z i ^{- 0 ;}

m i y i + m i L i ^sin(a i ^{) T} i + hyiyi + kyiyi - ку1У2 ^- P o ^{sin( a} )sin( ^ / )

m2^y2 + m2L2^sin(a2) Ф 2 + hy2^y2 + (kyi + ky2^)y2 ^- kyiyi ^{- 0}

⁽J1 + miL²⁾( &> i + miLico^s(a i) zi + mi Li sm^) yi +

+ hoi T 1 ⁺ koi T i ^- koi ^ 2 ^- P ₀ R ^{sin( m / )}

⁽J2 ⁺ m2L2₂) Ф ₂ ⁺ m2L2 ^{cos( a} 2 ⁾ z 2 ⁺ m2L2 ^{sin( a} 2 ⁾ y ₂ ⁺

+ h o 2 ⁽& 2 + (koi + ko2) Ф 2 — koi ^ i - 0

Расчетная схема колебательной системы ползуна может быть представлена следующим образом:

M_zz + h 3 z: + k 3 z - P_o cos( a ) sin( ro t ) + T ( y , t );

M_y_y + ( h ₁ + h ₂) y + ( h ₁ 1 ₁ - h ₂ 1 ₂) T & + ( k ₁ + k ₂) y + ( k ₁ 1 ₁ - k ₂ 1 ₂) T - P _o sin( a )sin( ro t );

J T + ( h 1 ,² + h ₂ 1₂ 2 )( p + ( h 1 ₁ - h ₂ 1 ₂) y + ( k ₁ 1 ² + k ₂ 1 ₂²) t + ( k ₁ 1 , - k ₂ 1 ₂) y - P _o R sin( ro t ),

Первое уравнение описывает колебания ползуна только по горизонтальному направлению, второе и третье уравнения взаимосвязаны и описывают колебания ползуна по вертикальному и угловому перемещениям. Для решения уравнений относительно координат y 1 и φ 1 представим их в операторном виде. Тогда решение системы относительно искомых координат имеет следующий вид y 1 = D y1 / D , φ 1 = D φ1 / D , где D – определитель системы, D y1 , D φ1 – определители, полученные из D путем замены столбцов, соответствующих у и φ на столбец правых частей уравнений. В результате преобразований получим передаточные функции колебательной системы в виде

W(y 1 )=y 1 /(P 0 sin(ωt)), W(φ 1 )=φ 1 /(P 0 sin(ωt))

В полученных выражениях числителя и знаменателя заменяем оператор р на iω . Получим в числителе и знаменателе комплексные числа. Необходимо передаточную функцию разделить на вещественную и мнимую части путем умножения на комплексное число, сопряженное с знаменателем. По полученным координатам в комплексной плоскости строится амплитудно-фазовая частотная характеристика. Вещественная часть координат откладывается по оси абсцисс, а мнимая – по оси ординат. Амплитудно-фазовая частотная характеристика системы стола для координаты у показана на рис. 2. Исходные данные для станка взяты из [1]. На рис. 3 показана резонансная кривая колебаний стола по оси у 1 , так называемая амплитудно-частотная характеристика. Для координаты φ 1 на рис. 4 показана амплитудно-фазовая частотная характеристика стола, а на рис. 5 – амплитудно-частотная характеристика. На следующих рисунках (6 и 7) представлены АЧХ станка и высокочастотная часть АФЧХ стола.

На рисунках передаточная функция представлена в форме амплитудно-фазовой частотной характеристики, которая отражает изменение фазы и отношения амплитуд колебаний выходной координаты к входной при синусоидальном изменении входной координаты. При этом частота синусоидальных колебаний входной координаты изменяется от нуля до бесконечности. Амплитудно-фазовая частотная характеристика является комплексной величиной. Модуль этой величины (радиус-вектор) равен амплитуде вынужденных колебаний (выходная координата), а аргумент (угол) равен фазе колебаний, т.е. разности фаз выходной и входной координат.

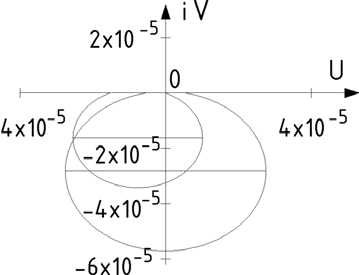
Рис. 2. АФЧХ стола по вертикальному перемещению

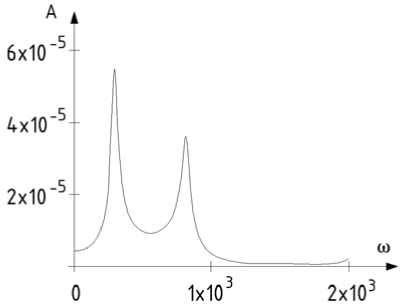
Рис. 3. АЧХ стола по вертикальному перемещению

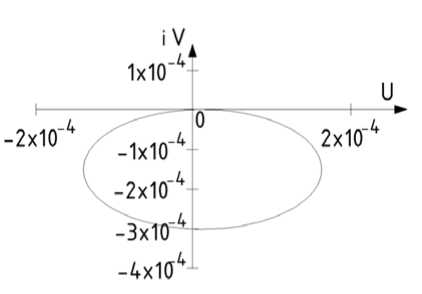
Рис. 4. АФЧХ стола по суммарному вертикальному перемещению

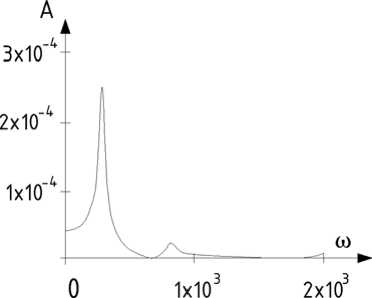
Рис. 5. АЧХ стола по угловому перемещению

A

4x10'^

ЗхКГ4

2x10"'*

1x10"4

to ►

О 1x103    2x103 ЗхЮ3

Рис. 6. АЧХ упругой системы станка

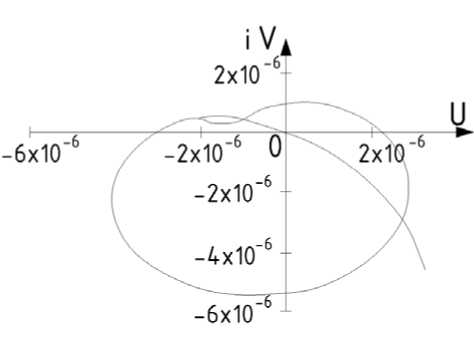
Рис. 7. Высокочастотная часть АФХЧ стола по суммарному вертикальному перемещению

Таким образом, для получения из уравнений движения амплитудно-фазовой частотной характеристики выводится передаточная функция, которая представляет собой отношение выходной координаты системы к входной. За выходную координату системы принимается координата соответствующего направления движения системы, для которой состав-ляется передаточная функция, за входную координату принимается возмущающее воздействие на систему в виде гармонической силы, совпадающей по направлению и величине с силой, действующей на систему. В соответствии с частотным методом анализа полученная передаточная функция преобразуется в выражение амплитудно-фазовой частотной характеристики системы. Полученная характеристика подвергается анализу с целью выяснения устойчивости системы при выбранных параметрах. Если система оказалась неустойчивой при заданных условиях работы, необходимо изменить ее параметры и построить новую характеристику. Такое построение с изменением параметров системы повторяется до тех пор, пока амплитуднофазовая частотная характеристика не примет вида, указывающего на необходимую устойчивость системы. В частности необходимо, чтобы левая ветвь этой характеристики, построенной в плоскости безразмерных координат, не охватывала точку на оси абсцисс с координатой минус единица.