Динамические характеристики стержневой конструкции крепления электрического ракетного двигателя на межорбитальном буксире

Одним из перспективных направлений развития космонавтики является освоение Луны с созданием обитаемых лунных баз с соответствующей инфраструктурой, орбитальной лунной посещаемой станции, добывающе-перерабатывающих комплексов с мощной энергетикой [1]. Первоочередной задачей в таком случае является создание эффективной транспортной системы для доставки грузов, в т. ч. неделимых, большой массы (до 30 т), с орбиты Земли на орбиту Луны [1–2].

Многоразовое использование элементов транспортной системы является одним из важнейших способов повышения эффективности транспортных операций в космосе. Ядерные электроракетные двигательные установки позволяют создать многоразовый межорбитальный буксир (ММБ) и тем самым повысить эффективность многозвенной космической транспортной системы.

Многоразовый межорбитальный буксир представляет собой транспортный космический летательный аппарат нового поколения, использующий для создания тяги электроракетную двигательную установку (ЭРДУ) [3]. Общий вид и состав ММБ представлен на рис. 1.

С целью снижения массы радиационной защиты от излучения реактора ядерной энергетической установки (ЯЭУ)

приборно-агрегатный отсек, ЭРДУ и транспортируемый полезный груз удалены от ЯЭУ на достаточно большое расстояние (25–50 м, в зависимости от мощности ЯЭУ). Электроракетный двигатель (ЭРД) соединяется с ЯЭУ с помощью протяженной многосекционной стержневой конструкции, консольно закрепленной на буксире. При значительной массе ЭРД и большом расстоянии между ЭРД и буксиром проектирование такой конструкции представляет собой отдельную задачу, решению которой посвящена данная работа.

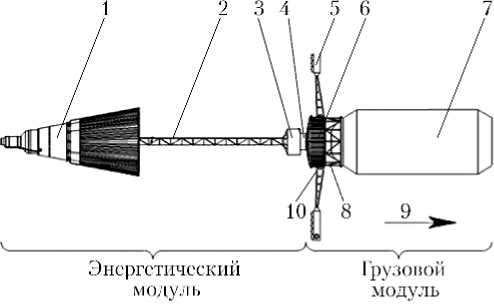
Рис. 1. Общий вид многоразового межорбитального буксира (ММБ): 1 — ядерная энергетическая установка; 2 — ферма системы отведения (трос системы безударного раскрытия и силовые кабели не показаны); 3 — приборно-агрегатный отсек; 4 — стыковочное устройство; 5 — секции электроракетного двигателя (ЭРД); 6 — отсек электроракетной двигательной установки с системой хранения и подачи рабочего тела; 7 — грузовой контейнер с полезным грузом; 8 — узел разделения ММБ и грузового контейнера; 9 — направление вектора силы тяги; 10 — ферма крепления ЭРД к ММБ

Первой задачей являлось исследование влияния параметров стержневой конструкции на первую собственную частоту [4–7]. Второй задачей был анализ напряженно-деформированного состояния (НДС) стержневой конструкции. При этом расчетным случаем являлся переходный процесс включения ЭРД. Третья задача состояла в проведении оптимального проектирования стержневой конструкции минимальной массы с ограничением на минимальное значение первой собственной частоты.

Описание расчетной модели

Расчет проводился методом конечных элементов. Модель выполнена из балочных элементов и закреплена по всем степеням свободы на нижнем торце. На верхнем торце закреплена сосредоточенная масса, имитирующая ЭРД. При исследовании динамических характеристик и НДС рассматривалось два типа ферменных конструкций, представленных на рис. 2.

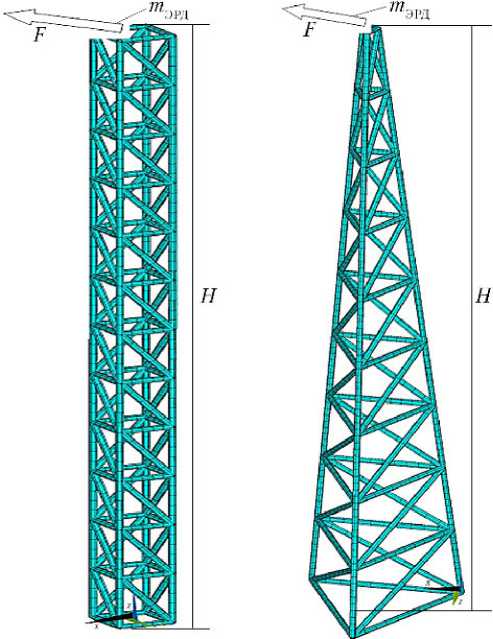
Рис. 2. Конечноэлементные модели ферменных конструкций крепления электроракетного двигателя

Примечание. H = 50 м; m _ЭРД = 70 кг.

Помимо расчета динамических характеристик также проводился поверочный расчет НДС оптимального проекта фермы. Расчетный случай — переходный процесс включения двигателя и достижения номинального значения тяги. Зависимость тяги ЭРД от времени, принятая в качестве исходных данных, представлена на рис. 3.

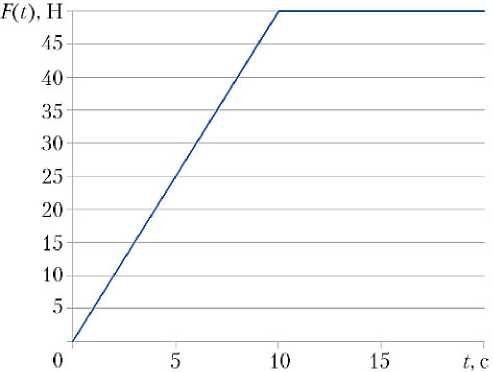
Рис. 3. Зависимость тяги электроракетного двигателя от времени

Масса перспективного ЭРД, имеющего тягу 50 Н, определялась экстраполяцией имеющихся данных о различных разработанных ЭРД и принималась равной 70 кг. На рис. 4 представлена экстраполяционная зависимость тяги ЭРД от массы.

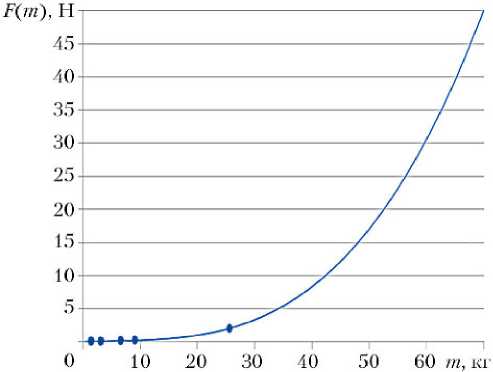
Рис. 4. Зависимость тяги электроракетного двигателя от его массы

Примечание. Синими точками отмечены характеристики стационарных плазменных двигателей, разработанных КБ «Факел» [8].

Параметры фермы принимались следующими: H = 50 м — высота фермы; m _ЭРД = 70 кг — масса ЭРД; m = 200 кг — масса фермы; d ₁ = 50 мм — внутренний диаметр стержней.

При фиксированных массе конструкции и диаметре стержней толщина стержней изменяется в зависимости от параметров конструкции согласно выражению:

, ( D 2 - D , )

H-—2— продольных секций принималось от 1 до 20 для обоих типов секций. Для конструкции с параллелепипедными и пирамидальными секциями радиус варьировался в пределах 1…14 м и 1…10 м, соответственно.

Стоит отметить, что при малом числе продольных секций длина стержней измеряется десятками метров, что, конечно же, конструктивно и технологически нереализуемо. Однако включение этих вариантов в область параметрического анализа было сделано с целью более глубокого понимания влияния варьируемых параметров на характер колебаний и значения первой собственной частоты, для чего и нужен параметрический анализ.

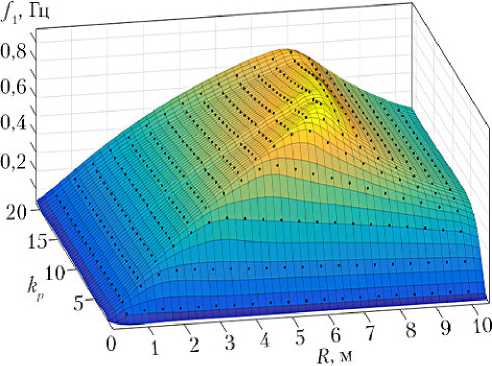
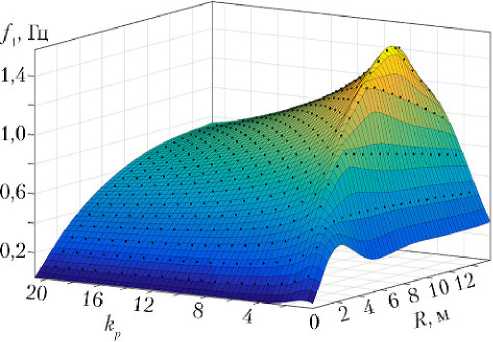
На рис. 5 представлена зависимость первой собственной частоты от количества продольных секций и радиуса основания. Характерные формы колебаний для всех возможных проектов представлены на рис. 6.

а)

где внешний диаметр стержней d ₂ определяется следующим уравнением:

d 2 =

4 m  , p /n + dl

где ρ — плотность материала; l — общая длина стержней.

При проектировании в качестве конструкционного материала рассматривался алюминиевый сплав АМг6.

Результаты параметрического анализа динамических характеристик и НДС

При расчетах варьировались R — радиус основания и k_p — количество продольных секций конструкции. Количество

б)

Рис. 5. Зависимость первой собственной частоты f1 от количества продольных секций kp и радиуса основания конструкции с параллелепипедной (а) и пирамидальной (б) секциями

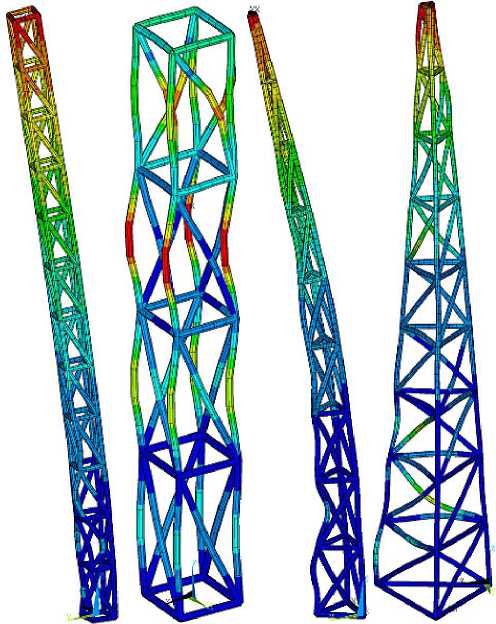
а)            б)           в)             г)

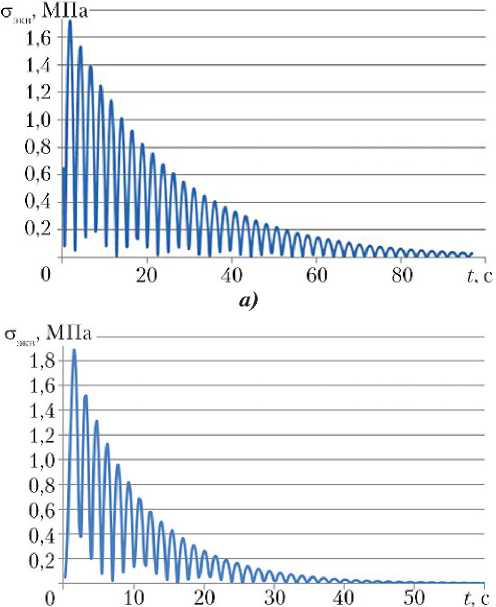
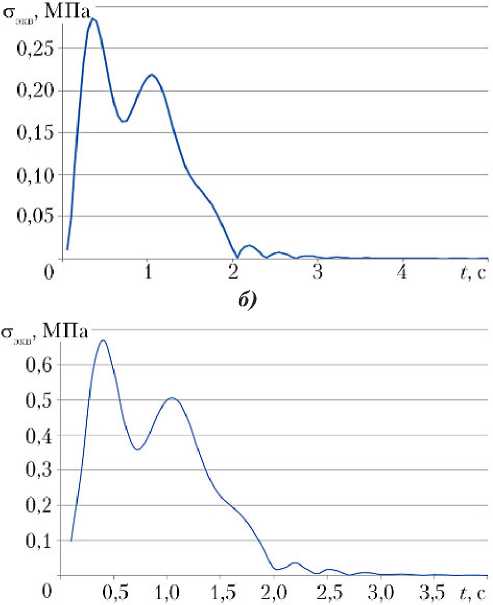
Для некоторых проектов с характерными балочной и оболочечной формами колебаний был проведен расчет НДС при переходном процессе включения двигателя. Зависимость максимальных эквивалентных напряжений в конструкции от времени представлена на рис. 7. Так как данные проекты обладают максимальной и минимальной первой собственной частотой, свойства всех остальных проектов находятся в диапазоне между ними.

Оптимальное проектирование

Конечной целью исследования динамических характеристик конструкции является проведение оптимального проектирования. Параметрический анализ в таком случае является первым этапом, позволяющим в первом приближении понять зависимость характеристик конструкции от ее параметров.

Постановка задачи оптимизации. Варьируемыми параметрами принимались следующие: k_p — количество продольных секций; R — радиус основания конструкции; d — диаметр стержней; h — толщина стержней. Данные параметры варьировались в следующих диапазонах: 10 ≤ k_p ≤ 20; 2 ≤ R ≤ 10 м; 40 ≤ d ≤ 100 мм; 1,5 ≤ h ≤ 3,0 мм.

Рис. 6. Формы колебаний проектов конструкции с па-раллелепипедными секциями с параметрами R = 2 м, kp = 20 (а); R = 11 м, kp = 4 (б) и пирамидальными секциями с параметрами R = 0,5 м, kp = 3 (в);

R = 7 м, kp = 7 (г)                               p

в)

г)

Рис. 7. Зависимость максимальных эквивалентных напряжений от времени при переходном процессе включения двигателя: конструкции с параллелепипедными секциями с параметрами R = 2 м, k_p = 20 (а); R = 11 м, k_p = 4 (б) и пирамидальными секциями с параметрами R = 0,5 м, k_p = 3 (в); R = 7 м, k_p = 7 (г)

Среди численных методов проведе- ния оптимального проектирования выделяется группа методов глобального поиска, которые направлены на исследование всей области допустимого изменения варьируемых параметров. Центральное место в этой группе занимает глобальный перебор, когда перебираются все возможные реализации проектируемого изделия и производится сравнение их критериев качества. Если варьируемые параметры непрерывны, то возможно проведение глобального перебора по сетке, нанесенной в пространстве поиска. Глобальный перебор — единственный численный метод, который в самом общем случае может гарантировать обнаружение глобального оптимума [9–10].

Критериями качества в данной задаче являются значение массы конструкции m и первой собственной частоты f ₁ . В данной задаче требовалось найти конструкцию минимальной массы, обеспечивающую выполнение условия f ₁ ≥ 1 Гц.

Решение задачи оптимального проектирования. Поскольку данная задача решалась численно, применение глобального перебора привело бы к значительным затратам машинного времени, необходимого для нахождения оптимального проекта. Варьирование всех четырех параметров приводит к ~10⁴ проектов, а расчет каждого из них занимает несколько секунд. Таким образом, расчет всех проектов занял бы десятки часов. Применение метода сгущения сетки поиска позволяет ускорить решение данной задачи в десятки раз.

Суть метода заключается в итерационном поиске оптимального проекта с уменьшением сетки около оптимального проекта на предыдущей итерации. Схема реализации метода глобального поиска со сгущением сетки для двухмерного пространства варьируемых параметров поиска показана на рис. 8. Сначала на грубой сетке в пределах заданного диапазона поиска f1min, f1max и f2min, f2max для параметров f1 и f2, соответственно, проводится расчет и находится оптимальный проект, которому соответствуют значения f1opt(1) и f2opt(1). Далее, от данного проекта как в сторону увеличения, так и в сторону уменьшения параметра откладывается интервал, равный половине шага варьирования параметра на предыдущей итерации. Данный интервал ограничивает поиск оптимального проекта на следующей итерации. При этом также уменьшается шаг. Таким образом, на второй итерации находится оптимальный проект с параметрами f1opt(2) и f2opt(2). Количество итераций поиска определяется проектантом.

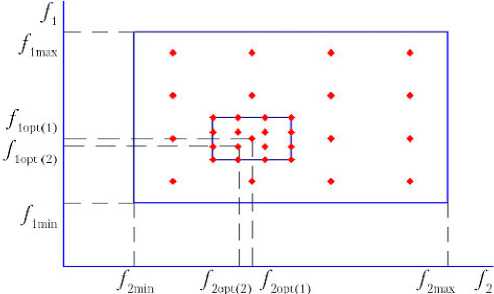
Рис. 8. Метод сгущения сетки поиска

В данной задаче проводилось две итерации, на каждой из которых рассчитывалось три значения для каждого варьируемого параметра. В табл. 1 и 2 приведены характеристики некоторых проектов и значения их параметров, рассчитанные на первой и второй итерациях. В табл. 1 и 2 проекты отсортированы по возрастанию массы конструкции.

Таким образом, оптимальным проектом для конструкции как с паралле-лепипедными, так и с пирамидальными секциями является проект 5. Видно, что оптимальный проект второй итерации на десятки процентов более выгоден с точки зрения минимума массы, чем оптимальный проект первой итерации, что говорит об эффективности применения метода ускорения поиска для проведения оптимального проектирования.

Помимо этого стоит отметить, что при проведении оптимального проектирования стержневых конструкций с обоими типами секций машинное время составило не более получаса. В данной задаче повышение размерности на единицу приводит к увеличению количества проектов и, как следствие, машинного времени, примерно в пять раз. Таким образом, при условии применения методов ускорения поиска оптимального проекта является вполне реализуемым проведение оптимального проектирования стержневых конструкций такого рода с варьированием шестисеми параметров, что говорит о довольно широких возможностях применения метода конечных элементов в задаче оптимального проектирования стержневых конструкций.

Таблица 1

Результаты итерационного расчета

Номер проекта	Параллелепипедная секция				Пирамидальная секция
	Итерация 1		Итерация 2		Итерация 1		Итерация 2
	f 1 , Гц	m , кг	f 1 , Гц	m , кг	f 1 , Гц	m , кг	f 1 , Гц	m , кг
1	1,02	752	—	—	1,05	380	—	—
2	1,05	942	—	—	1,08	410	—	—
3	1,02	762	—	—	1,02	419	—	—
4	1,00	1 050	—	—	1,05	453	—	—
5	—	—	1,00	570	—	—	1,02	304
6	—	—	1,01	605	—	—	1,00	314
7	—	—	1,00	627	—	—	1,04	317
8	—	—	1,00	580	—	—	1,04	320
9	—	—	1,02	618	—	—	1,02	328
10	—	—	1,01	641	—	—	1,03	332

Параметры проектов

Таблица 2

Номер проекта	Параллелепипедная секция				Пирамидальная секция
	k p	R , м	d , мм	h , мм	k p	R , м	d , мм	h , мм
1	11	4	80	1,5	9	4	40	2
2	11	4	60	2,5	9	4	60	1,5
3	11	4	60	2	12	4	40	2
4	14	4	60	2,5	12	4	60	1,5
5	9	4	50	1,87	7	4	35	1,9
6	9	4	50	2	8	4	35	1,9
7	10	4	50	2	7	4	40	1,8
8	9	4	55	1,75	7	4	35	2
9	9	4	55	1,87	8	4	40	1,8
10	10	4	55	1,87	8	4	35	2

Выводы

Параметрический анализ динамических характеристик стержневой конструкции крепления ЭРД показал, что при варьировании геометрических параметров динамические и прочностные характеристики конструкции могут изменяться в разы. Также меняется и сам характер колебаний и деформирования.

Проведение параметрического анализа численным методом позволяет проанализировать возможные свойства и предпочтительные значения параметров конструкции перед более подробной проработкой конструкции.

Использование пирамидальных секций при определенных соотношениях между геометрическими характеристиками позволяет существенно повысить значение первой собственной частоты. При этом максимальное значение напряжений при переходном динамическом процессе также существенно снижается, а при затухании колебаний уменьшается практически до нуля.

Метод конечных элементов может быть эффективно применен для оптимального проектирования многосекционных стержневых конструкций. При этом для обеспечения достаточно небольшого машинного времени эффективным является применение метода ускорения поиска оптимального проекта, к примеру, метода сгущения сетки поиска. В таком случае является возможным определение оптимальной конструкции с варьированием четырех и более параметров.